Journal of Financial Risk Management
Vol.04 No.03(2015), Article ID:60072,9 pages
10.4236/jfrm.2015.43013
Financial Risk Measurement for Turkish Insurance Companies Using VaR Models
Ismail Yildirim
Department of Finance, Banking and Insurance, Hitit University, Turkey
Email: ismailyildirim@hitit.edu.tr
Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 14 August 2015; accepted 27 September 2015; published 30 September 2015
ABSTRACT
This study aims to measure the foreign exchange risks that the insurance companies are exposed to. In this context, this study analyzes 7 insurance companies listed in Borsa Istanbul (Istanbul Stock Exchange). The foreign exchange risks that the insurance companies are exposed to were measured using VaR models, Historical Simulation and Monte Carlo Simulation methods. Data obtained from the analysis show the losses that the insurance companies suffer due to exchange risk. The losses calculated using the Monte Carlo Simulation were found to be greater than the losses calculated using Historical Simulation.
Keywords:
Insurance, Financial Risk, Foreign Exchange Risk, VaR

1. Introduction
It is possible to briefly define risk as a liability with potential loss. There are many risks that life insurance and pension companies are exposed to. However, the most significant risks arise from the core business of a company. These are risks that a company undertakes in return for premiums collected as a result of insurance contracts. Potential risks most commonly involve such risks.
As insurance industry constitutes an important part of the finance system especially in developed countries, it is exposed to financial risks. It is a common practice for insurance companies to invest in several financial assets in order to utilize the insurance premiums they have collected. Therefore, it is inevitable that insurance companies are faced with financial risks. Among the common risks other than insurance transactions that life insurance and pension companies are exposed to, there are financial risks such as interest rate risk, credit risk, liquidity risk, exchange rate risk. In addition, market risk, group risk, operational risk, modeling risk, and regulatory restrictions risk are also significant when it comes to insurance companies.
Financial risks involve two major factors. The first one is the deteriorations in the macroeconomic capacity as a result of political or economic crises both in national and international settings. As these kinds of risks arise from an imbalance in the system, they are also known as market or system risks. The second risk component is the unsystematic risks which commonly arise from the internal structure of a company and are defined by factors such as management quality, integrity of the financial structure, and the ability to be competitive. These two types of risks combined are called the “total risk”. Risk management models first define and classify the risks. The next step for risk management models is to measure and assess the risks while the third step involves the creation of a risk map in order to reduce these risks. The following processes involve continuous risk tracking and regular reports to the risk management department.
Insurance companies, when holding assets in the form of foreign currencies in order to meet their obligations, are exposed to foreign exchange risk. This type of risk results from the fluctuations in exchange rates. This practice creates a threat in terms of foreign exchange rate when the company is indebted in foreign currencies. Insurance companies take foreign exchange risks into consideration as part of their assessments for the next twelve months when calculating their minimum capital requirements. The foreign exchange risk is a factor not just insurance and reassurance companies but any company must take into consideration (Insurance Europe, 2013) . According to Giddy & Dufey, foreign exchange risk is “the impact of the unpredictable exchange rate changes on a company” (Giddy & Dufey, 2006) .
The foreign exchange risk cannot be eliminated altogether yet, there are several solutions in order to minimize its impact. The foreign exchange risk is especially an important issue for international companies. The research showed that the profits of international companies were affected by the fluctuations in the exchange rates (Popov & Stutzmann, 2003) .
This study aims to measure the foreign exchange risk that the insurance companies are exposed to. For this purpose, this study measures the risks arising from exchange rate positions of 7 insurance companies listed in Borsa Istanbul (BIST).
2. Literature Survey
Value at Risk is a measure which can be used for any company which is exposed to financial risk. It is commonly used by banks, insurance companies, pension funds, and other financial corporations for which risk management is a must (Jorion, 2000) . Literature shows that studies on Value at Risk mainly focus on such organizations.
Assaf (2015) , Su (2015) , Iglesias (2015) , and Baciu (2014) used Value at Risk in order to measure the risks stock markets are exposed to. Assaf (2015) investigated the performance of stock markets operating in MENA (Middle East and North Africa) countries using the Value at Risk method. Su (2015) investigated the performance of stock markets operating in developing countries using the Value at Risk method. Iglesias (2015) analyzed the stock markets operating in the EUROZONE using the Value at Risk method for a period between 2000 and 2012. Baciu (2014) calculated the risk of the Romanian stock market using the Value at Risk method.
Keçeci & Sarul (2014) , Adams et al. (2014) , Janssen (2009) , and Majumdar (2008) have conducted Value at Risk calculations for insurance and financial organizations. Adams et al. (2014) assessed the direction, extent and duration of the risk dispersion between financial organizations using Value at Risk methods. Keçeci & Sarul (2014) turned to VaR methods in order to measure the market risk Turkish insurance companies are exposed to. Majumdar (2008) measured the insurance risks using historical simulation and Monte Carlo simulation, methods used in VaR calculations. Janssen (2009) measured the portfolio risks European insurance companies are exposed to as part of Solvency II using VaR methods.
This study measures the foreign exchange risk of 7 insurance companies operating in Turkey listed in Borsa Istanbul are exposed to using Value at Risk methods. In this respect, this study is expected to contribute to the literature.
3. Data and Methodology
This study uses Value at Risk methods in order to measure the foreign exchange risk insurance companies are exposed to. Value at Risk is a method commonly used in order to measure the market risk.
Value at Risk is a risk measure first developed by J.P. Morgan in 1994 to estimate the loss expected for a fixed portfolio for a time period of “t” with a specified “p” probability value. Thus, it is possible to measure the total risk a portfolio is exposed to with a single number. Being a simple and easy-to-use method, this technique is quickly adopted by several financial organizations and has gained widespread use (Iorgulescua, 2012) . It gained widespread use in risk measurements especially after the Financial Crisis of 2008 (Piroozfar, 2009) .
Stress testing for portfolio performance measurements in extraordinary market conditions is used in addition to the VaR methods which is ideal for normal market conditions. This is shown in Figure 1.
Risks occurring from extraordinary market conditions and extreme price movements influence the condition of the portfolio (BIS, 2005, 4) . The Value at Risk methods used is classified into two groups, namely, Parametric Methods (Variance-Covariance Method) and Non-Parametric Methods (Historical Simulation, Monte Carlo Simulation Methods).
3.1. Historical Simulation Method
Historical Simulation Method involves the application of asset returns of a time series of past 250 days to the current portfolio weights (Bolgün & Akçay, 2009) .
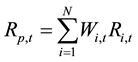
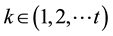
W: Current weight of the risk factors in a portfolio
R: Change in returns
Probable portfolio value is estimated using the changes in return for w weights and a time period of t, and VaR is calculated for a confidence level of 95% or 99%. The full valuation method involves the whole set of prices while Historical Value at Risk requires efficiency curves which proves the realism inherent for this method.
Thus, the model risk decreases while it is fully eliminated when not available in the data. Therefore, this method can be used as both linear and nonlinear investment tools (Manganelli & Engle, 2001) .
The criticism about this method focuses on the disadvantage arising from ignoring some risks by failing to consider possible future changes as the method focuses on the changes in the sample being based on historical data (Pallotta & Zenti, 2000) .
3.2. Monte Carlo Simulation Method
Monte Carlo Simulation requires the generation of various random numbers in order to reach the correct VaR. Random number generation should be increased by 100-fold in order to increase the accuracy of VaR by a digit (Glasserman, 2004) . Nevertheless, Monte Carlo Simulation is commonly used in stress testing (Guo, 2008) .
Parameters Used in the Value at Risk Measurement.
VaR calculations depend on a number of parameters. These are holding period, confidence level, sampling period and calculation of capital requirement.
3.3. Holding Period
Considering Value at Risk is based on the measurement of the price changes of a portfolio or an individual asset
Figure 1. Value at Risk. Source: BIS, 2005.
in a “certain time period”, the holding period is a parameter concerning the time period in which assets will be held in the portfolio. In other words, the holding period is the time horizon in which the change in the portfolio value is to be calculated (Assaf, 2015) .
The holding period is calculated by taking the square root of the period as part of the VaR calculations (Iglesias, 2015) .
1 day holding period =  = 1
= 1
10 days holding period = 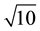 = 3.162278
= 3.162278
21 days holding period =  = 4.582576
= 4.582576
252 days holding period = 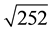 = 15.87451
= 15.87451
The VaR calculated for a holding period is multiplied with the square root of that holding period which VaR is to be calculated for. Therefore, the result obtained for a holding period of 10 days is higher than the result obtained for a holding period of 1 day. The VaR increases as the holding period increases.
3.4. Confidence Interval
Confidence interval should be estimated beforehand in VaR calculations. The confidence level is determined based on the company’s risk appetite and its economic capital stock (Yildirim, 2012) . Standard VaR calculations aim to measure potential future losses in a specified confidence level (commonly 95% or 99%) (Bolgün & Akçay, 2009) .
Confidence level when defined as 99% for VaR estimation means that the probability of the maximum loss for a day exceeding the VaR level is only at 1%. The VaR value calculated increases with the increasing confidence level.
3.5. Sampling Period
Another parameter of the Value at Risk (VaR) measurements is the determination of past observation periods for which the volatility and correlations will be calculated and price changes will be observed.
The success of VaR calculations depends on the dataset to be used in volatility and correlation calculations. Volatility values calculated for different sampling periods will give different results therefore resulting in different VaR values. The Basel Committee defined a minimum of a year (252 working days) as the sampling period and obliged companies to update their dataset in specific intervals and to calculate VaR according to the new dataset (Basel Committee on Banking Supervision, 2009, 13) . The sampling period shall be no less than a year (250 working days).
3.6. Capital Requirement Calculation
Capital requirement calculation is not a primary parameter of VaR calculations. However, capital requirement will be calculated for the market risk following the VaR calculation. In other words, risk exposure should be stated in capital in order to make it possible to compare capital costs of all risks in a common plane. Therefore, Bank for International Settlements (BIS) set the capital coefficient to be 3 at a minimum. This value alternates between 3 and 4. The BIS is subject to serious criticism on this subject. Some claim that this capital coefficient lacks the necessary basis. Actors of the market find this coefficient higher than it should be (Bolgün & Akçay, 2009) .
It is a common practice for banking organizations to associate VaR results with their capital adequacy by multiplying the VaR results with the capital coefficient, 3 as part of the capital requirement calculations. Yet, there are no standards defined for the insurance companies.
Insurance companies included in this study and their exchange rate positions are shown in Table 1 and Table 2.
This study analyzes 7 insurance companies operating in Turkey listed in Borsa Istanbul. 6 of these insurance companies focus their activities in fields other than life insurance while 1 of them operates in life insurance. It was not required to calculate the risks life insurance companies and others are exposed to separately as financial risks were in question. Exchange rate positions of the insurance companies included in the analysis are given in Table 2.
6 of the insurance companies have a positive foreign exchange position. In other words, they do not have a
Table 1. Insurance companies which are included in the analysis.
Table 2. Exchange rate positions of the insurance companies.
foreign exchange deficit. Only Aviva insurance had a negative foreign exchange position. USD and Euro were included in the study in terms of foreign exchange positions of the companies. Other currencies which account for small amounts were not included in the foreign exchange positions of insurance companies. In addition, amounts which were listed under the “other” option were not included in the portfolio.
Net positions of the insurance companies in USD and Euro as stated in their balance sheets were calculated in Turkish Lira dividing the amounts by the average exchange rates issued by the Central Bank of Turkey for the date of 31.12.2014 (USD = 2.1343; Euro = 2.9365).
The analysis was based on the daily exchange rates for 252 working days between 01.01.2014 and 31.12.2014. It is required to take data for at least 252 days into account when calculating the VaR. Figure 2 shows the value of the Euro and USD against Turkish Lira.
The analysis involved the value of the Euro and USD for 252 days. According to the increases and decreases in the value of the USD (Figure 2) it was found that the maximum increase in the value accounted for 5% while the maximum decrease in the value accounted for 4%. The Euro, on the other hand, suffered a value loss by 6% against the Turkish Lira in 2014 while increasing by over 4% for the same period.
4. Empirical Findings
The first phase of this study involved calculations of the Value at Risk for insurance companies in question. The second phase involved the estimation of the impact of Value at Risk on the capital adequacy ratios of these insurance companies. The Calculations involved Historical Simulation Method and Monte Carlo Simulation Method with a confidence level of 99% and holding periods of 1 and 10 days.
Descriptive statistics for foreign exchange rates used in the market risk calculations are shown in Table 3.
The skewness and kurtosis coefficients need to be investigated in order to look into the distribution structure of the return series with irregular distribution. Skewness measures the symmetry of the distribution while
Figure 2. Euro and USD exchange rate changes.
Table 3. Descriptive statistics for foreign exchange rates.
kurtosis measures the peakedness of the distribution. A normal distribution gives a skewness coefficient of 0 while giving a kurtosis coefficient of 3. The skewness coefficient values greater than 0 implies that the distribution is left-skewed; while values smaller than 0 implies that the distribution is right-skewed. Kurtosis, on the other hand, gives information about the distribution frequencies if they are accumulated around the average or if they diverge from the average in order to form a flat structure. Kurtosis coefficient values greater than 3 implies that the distribution is peaked; while values smaller than 3 implies that the distribution is flat.
Considering the skewness coefficients of the foreign exchange rates in question, it was found that the skewness coefficients of the Euro and USD were both greater than 0. This means that the return distribution of these currencies was left-skewed. Kurtosis coefficients of the Euro and USD distributions were smaller than 3 and it was found that the distributions were flat-topped.
The foreign exchange rates in question do not exhibit normal distribution characteristics. As Historical Simulation Method does not require estimation of any parameters such as volatility or correlation, misinterpretation of the parameters was not an issue.
4.1. Results of the Historical Simulation Method
Results of the Historical Simulation Method give the maximum expected loss for a time interval of 252 days under normal market conditions with a confidence level of 99%. The results obtained from the Historical Simulation Method against Foreign Exchange risk are shown in Table 4.
When the Historical Simulation results of the insurance companies were analyzed it was found that their daily losses ranged between 0.59 and 1.75. Halk Insurance suffered the greatest loss with 1.75%. The losses insurance companies suffer increased with the increasing holding periods. Losses calculated for a holding period of 10 days range between 1.86% and 5.54%.
Table 4. Historical simulation method results for insurance companies based on foreign exchange risk.
4.2. Results of the Monte Carlo Simulation Method
Monte Carlo Simulation Method reveals the most unfavorable conditions insurance companies may face under normal market conditions with a confidence level of 99%. Results of the Monte Carlo Simulation against the Foreign Exchange risk are shown in Table 5.
When the results given in Table 5 are analyzed it was found that daily losses ranged between 0.35% and 0.93%. Güneş Insurance suffered the greatest daily loss with 0.93%, while Ak Insurance suffered the lowest daily loss with 0.35%. According to the VaR results obtained from a holding period of 1 day using the Monte Carlo Simulation, Ak Insurance suffered the second greatest loss with 0.90%.
When the Value at Risk positions were calculated using the Monte Carlo Simulation is proportioned to their current values; daily losses with respect to a holding period of 10 days was found to be in a range between 1.10% and 2.95%. Güneş Insurance suffered the greatest loss with 2.95% according to the Monte Carlo Simulation results obtained from a holding period of 10 days. The lowest loss, on the other hand, was 1.10% in the case of Ak Insurance. Halk Insurance suffered the second greatest loss with 2.85% according to the results obtained from a holding period of 10 days.
VaR results obtained using the Historical Simulation Method for holding periods of 1 day with a confidence level of 99% were higher than those calculated using the Monte Carlo Simulation. Similarly, the results obtained for a holding period of 10 days is higher than the results obtained for a holding period of 1 day.
4.3. Association of VaR Results with Capital Adequacy
Capital adequacy correlation is a necessary process in order to determine the impact of the VaR results on the capital adequacy of insurance companies. Especially the regulatory and auditing authorities will be interested to see the erosion in the capital adequacies of insurance companies caused by the VaR results.
We have mentioned that the Bank for International Settlements (BIS) identified a capital coefficient at a minimum of 3 for the calculations of capital adequacy according to the Value at Risk (VaR) results. However, several authorities claim that this capital coefficient lacks the necessary basis. In fact, when the capital coefficient is taken 3 in the correlations between the VaR results and capital adequacies it would take the capital adequacy ratios to a lower level. Banking Regulatory and Supervisory Agency also recommends the capital coefficient to be taken 3. Yet, there are no standards defined for the insurance companies in Turkey in this respect. This study used the capital coefficient of 3 in the correlations between the VaR values of insurance companies and their capital adequacy ratios.
Table 6 shows the current capital adequacy ratios of insurance companies as of 2014.
Insurance companies operating in Turkey calculate their capital adequacy ratios by dividing their capitals by their minimum required capital. According to the capital adequacy ratios obtained, capital adequacy ratio of Aviva Insurance is found to be below 100. Anadolu Life Insurance was found to be the insurance company with the greatest capital adequacy ratio.
The required capital is most commonly calculated using two methods in Turkey. According to the first method, the capital is calculated separately for fields such as insurance other than life insurance, life insurance and pension. This method involves the use of the highest of the two amounts found based on the premium and dam-
Table 5. Monte Carlo simulation results for insurance companies based on foreign exchange risk.
Table 6. Capital adequacies of the insurance companies.
*Capital/Minimum Required Capital. Source: 31.12.2014 Balance Sheet Annotations.
Table 7. The impact of foreign exchange risk analysis on the capital adequacy of insurance companies.
*1-day VaR results are multiplied by 3 capital factor.
ages for insurance other than life insurance and the use of the total amount for results related to obligation and risk for life insurance. According to the second method, required capital equals to the sum of active risk, reassurance risk, risk of overly increased premiums, risk of provision for outstanding claims, notation risk and foreign exchange risk.
Insurance companies operating in Turkey most commonly prefer the first method when calculating the minimum required capital. The minimum required capitals included in this study are directly taken from the balance sheet annotations of the insurance companies in question.
The impacts of the Historical and Monte Carlo Simulation Methods on the capital adequacy ratios were found at different levels (Table 7). Values obtained from the Historical Simulation Method have taken the capital adequacy ratio to a point lower than the ones obtained from the Monte Carlo Simulation Method. However, this decrease was not significant. The VaR results obtained appears to have no adverse impact on the capital adequacy ratios.
5. Conclusion
Insurance companies are exposed to financial risks as it is the case for any other financial organization due to their assets and their obligations. Among these risks, financial risks are risks such as foreign exchange risk, interest rate risk, credit risk, and liquidity risk. Aforementioned risks have an impact on the operations of insurance companies to a degree close to the banking industry and they tend to result in loss when they are realized.
This study measured the foreign exchange risks which insurance companies may be exposed to using the VaR models. 7 insurance companies listed in Borsa Istanbul were analyzed. Value at Risk was calculated for the foreign exchange positions of insurance companies. The results showed that:
Results obtained from the Historical Simulation Method were higher than those obtained from the Monte Carlo Simulation, both being methods of the VaR calculation. Similarly, the losses calculated for a holding period of 10 days were higher than the ones calculated for a holding period of 1 day. The VaR results obtained appear to have no adverse impact on the capital adequacy ratios.
Cite this paper
IsmailYildirim, (2015) Financial Risk Measurement for Turkish Insurance Companies Using VaR Models. Journal of Financial Risk Management,04,158-167. doi: 10.4236/jfrm.2015.43013
References
- 1. Adams, Z., Füss, R., & Gropp, R. (2014). Spillover Effects among Financial Institutions: A State-Dependent Sensitivity Value-at-Risk Approach. Journal of Financial and Quantitative Analysis, 49, 575-598.
http://dx.doi.org/10.1017/S0022109014000325 - 2. Assaf, A. (2015). Value-at-Risk Analysis in the MENA Equity Markets: Fat Tails and Conditional Asymmetries in Return Distributions. Journal of Multinational Financial Management, 29, 30-45.
http://dx.doi.org/10.1016/j.mulfin.2014.11.002 - 3. Baciu, O.A. (2014). Value-at-Risk Estimation on Bucharest Stock Exchange. Journal of Applied Quantitative Methods, 9, No. 4.
- 4. Basel Committee on Banking Supervision (2009). Revisions to the Basel II Market Risk Framework.
http://www.bis.org/publ/bcbs158.htm - 5. BIS (2005). Stress Testing at Major Financial Institutions: Survey Results and Practice. Working Group Report, Committee on the Global Financial System, Bank for International Settlements, BASEL, Switzerland.
- 6. Bolgün, K. E., & Akçay, B. (2009). Risk Yönetimi. Istanbul: Scala Yayincilik.
- 7. Giddy, I., & Dufey, G. (2006). The Management of Foreign Exchange Risk. New York: New York University, Stern School of Business.
http://pages.stern.nyu.edu/~igiddy/fxrisk.htm - 8. Glasserman, P. (2004). Monte Carlo Methods in Financial Engineering. New York: Springer.
- 9. Guo, L. (2008). Effective Stress Testing in Enterprise Risk Management.
http://file:///C:/Users/Fujitsu/Downloads/mono-2008-m-as08-1-guo%20(1).pdf - 10. Iglesias, E. M. (2015). Value at Risk and Expected Shortfall of Firms in the Main European Union Stock Market Indexes: A Detailed Analysis by Economic Sectors and Geographical Situation. Economic Modelling, 50, 1-8.
http://dx.doi.org/10.1016/j.econmod.2015.06.004 - 11. Insurance Europe (2013). Currency Risk, Briefing Note.
http://financial-stability.org/research/artikel/2013/2013-q1/2013-q1-detail/date/2013/march/article/solvency-ii-currency-risk-module-flawed/ - 12. Iorgulescua, F. (2012). Backtesting Value-at-Risk: Case Study on the Romanian Capital Market. Procedia—Social and Behavioral Sciences, 62, 796-800. www.sciencedirect.com
- 13. Janssen, M. J. J. (2009). Portfolio Optimization with a Value at Risk Constraint in the Presence of Unhedgeable Risks. Amsterdam: Department of Quantitative Economics, University of Amsterdam.
- 14. Jorion, P. (2000). Value at Risk: The New Benchmark for Controlling Risk (2nd ed.). New York: McGraw-Hill Inc.
- 15. Keçeci, F. N., & Sarul, L. S. (2014). Application of Value at Risk (VaR) Models on Insurance Claim Data. Digital Proceeding of the ISDS’2014, Side, 10-14 May 2014.
- 16. Majumdar, C. (2008). VaR (Value at Risk) for Insurance Risk—A Simple Model. 10th Global Conference of Actuaries, 7-8 February 2008.
- 17. Manganelli, S., & Engle, R. F. (2001). Value at Risk Model in Finance. European Central Bank Working Paper Series, 75, 1-40.
- 18. Pallotta, M., & Zenti, R. (2000). Risk Analysis for Asset Managers: Historical Simulation, the Bootstrap Approach and Value at Risk Calculation. RAS Asset Management.
http://papers.ssrn.com/sol3/papers.cfm?abstract_id=251669 - 19. Piroozfar, G. (2009). Forecasting Value at Risk with Historical and Filtered Historical Simulation Methods. U.U.D.M. Project Report, Uppsala: Department of Mathematics, Uppsala University.
- 20. Popov, V., & Stutzmann, Y. (2003). How Is Foreign Exchange Managed: An Empirical Study Applied to Two Swiss Companies. Master’s Thesis, Lausanne: University of Lausanne.
- 21. Su, B. J. (2015). Value-at-Risk Estimates of the Stock Indices in Developed and Emerging Markets Including the Spillover Effects of Currency Market. Economic Modeling, 46, 204-224.
- 22. Yildirim, I. (2012). Stress Testing in Risk Management: An Application in the Turkish Banking Sector. International Journal of Trade, Economics and Finance, 3, 441-444.





