ABSTRACT

With the rising importance of China’s role in the world economy, the Chinese economic fluctuation has become a more and more significant factor that influences the world economy. Therefore, it is an interesting issue for all circles as well as academicians that whether the real economic interconnection leads to volatility spillover between China’s and international stock markets. In this paper, CGARCH (Combine Generalized Auto Regressive Conditional Heteroskedasticity) model and Granger causality test are applied to examine the relationship between China’s A share index and world’s major indices with respect to the extreme risk spillover effect. The results show that the extreme risk of A share market’s long-run volatility component has strong risk spillover effect on foreign markets, while the short term volatility is vulnerable to the risks from overseas. Since long-run volatility component is consistent with real economic cycle, our results support that China’s economy has deep impact on world economy.

Keywords:Volatility, Granger Causality Test, Extreme Risk

1. Introduction

With a history of 21years, Chinese stock market has developed rapidly. In particular, a series of creative reform measures have been adopted by China Security Regulatory Commission in recent years. For example, holistic listing and listing of A + H (A-share market and H-share market) have transformed the increase of macro economy into the profits of listed companies and improved the investment appeal for stock market as well as made a great contribution to reforms both of state-owned enterprises and of banks. Furthermore, the share-trading reform, which was initiated on May 8^th, 2005, reconciled the divergence of interests between holders of tradable shares and those of non-tradable shares from the perspective of system. This reform also perfected the pricing mechanism of stock market and to some extent prevented the excessive price fluctuation of the market which separated from the basic aspect of listed companies. In addition, the major background of development of Chinese stock market is the rising importance of China’s role in world economy. The Chinese economic fluctuation has become a more and more significant factor that influences the world economy. For example, China’s increasing demand on bulk commodity to some extent promote the rise in certain goods’ prices and China’s macro-economic policies and fluctuation of real economy would bring about the price fluctuation of bulk commodity. In that case, an issue raised is that whether the real economic interconnection leads to volatility spillover between China’s and international stock market.

This paper focuses on the issue that whether the sharp fluctuation of domestic stock market will have an impact on the international market. The event happening on 27^th, February, 2007 is a typical example. On that day, the Shanghai A share index slumped by 8.85%, leading to a loss of over one trillion for the market value of two domestic stock markets within one trading day, which caused the international market concerning about China’s economy. The next day，the largest one-day percentage drop of Dow Jones Industrial Average occurred since September 11 attacks, which was a significant effect from extreme risk of China’s market on oversea ones. However, it is a controversial issue that whether China’s stock market can have an important impact on world markets. Through empirical study, this paper analyzes the relationship between Chinese and world stock markets with respect to the extreme risk spillover effect. This research is of great help for investors and regulatory departments to have an objective view on the positions of China’s stock market throughout the world as well as to enhance their awareness of risk prevention.

The domestic and oversea studies concerning the relationship between China’s and international markets have shown that China’s stock market didn’t significantly depend on international markets in early years especially before Southeast Asia Crisis (Bailey, 1994; Johnson, Sun, & Soenen, 1994; Huang, Yang, & Hu, 2000). Having analyzed the data from January 2^nd, 1995 to April 4^th, 2003, Hong and others (Hong, Cheng, Liu, & Wang, 2004) concluded that Chinese stock market had some slipover risk with other Asian markets while had few or no slipover risk with global developed securities markets. Such empirical studies varied in sampling, making different conclusions. Moreover, it is worth noting that the volatility of a market will have various impacts on other markets, such as the interconnection between volatilities and that between extreme risks. In terms of methodology, the studies above have focused on the transmission between risks sharing the same property, while the interconnection between risks with different properties was excluded. For example, the extreme risk of one market may not affect others but can bring about temporary disturbance with conditional fluctuation.

In this paper, Granger causality test is applied to examine the relationship between China’s and international stock markets with respect to the extreme risk spillover effect, namely the influence of one market’s extreme risk on another market’s volatility.

2. Data and Model

Regarding the technological methods to study the market relevance, two problems should be solved. One is the choice of variable measuring the characteristics of stock market. The conditional variance of return can be adopted to test the volatility spillover effect. Through establishing such models like GARCH (Generalized Auto Regressive Conditional Heteroskedasticity) and SV (Stochastic Volatility), the fluctuation of variance is tested to study the topic of spillover (Hamao, Masulis, & Ng, 1990; Lin, Engle, & Ito, 1994; King, Sentana, & Wadhwani, 1994; Engle & Lee, 1999; Chan, Karolyi, & Stulz, 1992). VaR (Value-at-Risk) model is used for the study on spillover of extreme risks (Hong, Cheng, Liu, & Wang, 2004). We can also use the rate of return co-integration relation to analysis the stock market of Chinese mainland and Hong Kong (Wu & Pan, 2005).

For the first problem, we chose CGARCH (Engle & Lee, 1999) which can provide long-and short-run components of volatility to present a more comprehensive view of volatility characters. Another aspect of technical method is the choice of the measurement methods for these variables, such like all kinds of regression methods, co integration test and Granger causality test. The purpose is to test volatility features and the features leading to volatility in long-and short-run interconnections between markets. With many lag phases, the regression model and co integration test are inappropriate to investigate the connections between variables. We therefore chose Granger causality test.

1) Yield Data We have a research on Shanghai A share index and 9 barometer stock price indices of international stock markets, which are DJI (Dow Jones Average Price Index), N225 (The Nikkei 225), HIS (Hang Seng Index), KS11 (Korea Stock Price Index), FTSE (Financial Times Stock Indices), GDAXI (Germany’s DAX 30 Index), FCHI (The French Cac 40 Index). Assuming that P_t is the stock price at time t, we define the daily return at time t as follows:

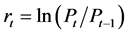
2) Choice of Volatility Measurement Indicators It has been found out that the volatility model with double components can reflect the return volatility better than that with single component (Engle & Lee, 1999; Engle & Rosenberg, 2000; Alizadeh, Brandt, & Diebold, 2002; Bollerslev & Zhou, 2002; Chernov, Gallant, Ghysels, & Tauchen, 2003; Chacko & Viceira, 2003). The market expects different risk return for different volatility components. (Malkiel, 1979) believes that only permanent volatility can bring about significant change of risk return. (Adrian & Rosenberg, 2008) further argue that the short-run component captured economic cycle risk, while the long-run component relates closely to business cycle risk. Therefore, we choose the CGARCH model as the basis of empirical model.

The following is GARCH model with single volatility component:

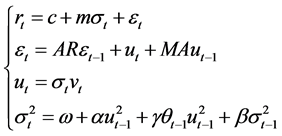(1)

r_t is the yield, while c, m, AR, MA, a, b and g represent regression coefficient. The serial correlation of yield can cause that of volatility. We assume that Residual e_t obeys a ARMA (Auto Regressive And Moving Average) process and it is obvious that a positive first covariance exists when AR + MA > 0. 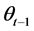is a dummy variable., if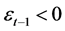; otherwise,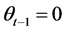. n_t obeys the standard normal distribution. This model assumes that the conditional variance obeys a process of mean reversion around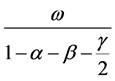. The Model CGARCH amends the wave equation:

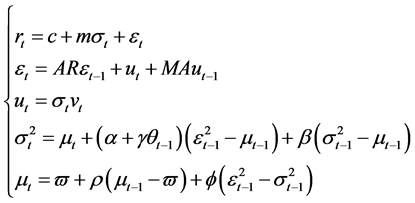(2)

The Model CGARCH assumes that the mean reversion of conditional variance 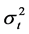is m_t changing with time. As a result, this model not only describes the short run conditional volatility like GARCH models, but also can capture the variation characteristics of long run volatility: when 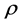is very close to 1 (often range from 0.99 - 1), m_t will end up with at a very slow speed.

We also choose 2 variables from Model (2) as the indicators to measure volatility features: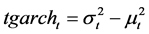,. Therefore, tgarch_t reflects the short run components of volatility while pgarch_t reflects long run components.

The slump of A-share market gives rise to different responses in the volatility of international stock market: the United States market is more volatile than other markets. In that case, the regular volatility of a market can be different from the extreme risk spillover effect, that is to say, the extreme risk may not cause another extreme risk and has limited influence. Therefore, the causality test for two markets’ volatility with the same quality may not accurately reflect the interconnection between markets. Thus, it is necessary to investigate the influence of extreme risk on conditional volatility. We define the 0.9 Fractile quantile from each sample of long-run and short-run volatility as the threshold of extreme risk. Once the tgarch_t (or pgarch_t) exceeds the threshold, we believe that the extreme risk happens. To be more specificqtgarch_t = 1, if tgarch_t > quantile (0.90, sample data, tgarch_t)qtgarch_t = 0, other.

qpgarch_t = 1, if pgarch_t > quantile (0.90, sample data, pgarch_t)qpgarch_t = 0, other.

The quantile (a, s, d) “a” fractile quantile in given sample interval “s” of sequence “d”.

To diffrentiate the attribution of volatiltiy indicators for different markets, we add a prefix. For example, the volatility indicators of market A are expressed as A_tgarch_t, A_pgarch_t, A_qtgarch_t, A_qpgarch_t respectively.

3) Granger Causality Test

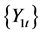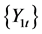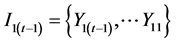To investigate that whether the change of volatility indicator in a market causes similar change in another market (Granger, 1969; Granger, 1980). We define that, and and are the information sets of Market 1and Market 2 at moment respectively. If

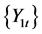We can figure out that can Granger-cause on information set.

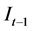In econometric model, mean Granger Causality which is widely used is the special case of the above concept, i.e. it considers whether 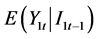equals to.

To be more specific, the null hypothesis that X does not Granger-cause Y is the estimation on the two regression models below:

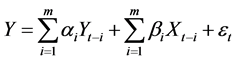(unlimited conditional regression)

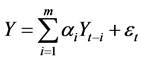(limited conditional regression)

The residual sum of squares of each regression are used to calculate the F-statistic and to test whether the coefficient 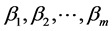do not significantly equal to 0 at the same time. A problem in application is the choice of the lag length m. We usually determine it after choosing different lag length for observation or selecting the best model based on AIC (Akaike Information Criteria). Since there might be a rather long lag length between the influence of long run volatility and volatility coefficient in those observed variables, as well as the best lag lengths are different among different markets and different indicators, we choose a large amount of lag lengths for testing range from 1 to 50, in order to make a unified pattern analysis on every market and indicator. If a number of successive lag lengths prove that there is connected effect between them, we can confirm the conclusion with confidence. This is the ergodicity analysis on testing the stability of Granger causality As for the focus of this paper, we will test the influence of each other’s conditional volatility between extreme risks of Market A and Market B, that is to say, we will put the volatility indicators of A and B into one group and test the influence of Market A’s extreme risk on the short run conditional volatility of Market B and vice versa. To be more specific, 1) we define X = A_qtgarch_t, Y = B_tgarch_t and then investigate the influence of A’s short run extreme risk on the short run conditional volatility of Market B; to research on the effect of B’s short run extreme risk on A’s short run conditional volatility, we will define X = B_qtgarch_t, Y = A_tgarch_t. 2) We make X = A_qpgarch_t, Y = B_pgarch_t to study the influence of A’s long run extreme risk on B’s short run volatility; to study the effect of B’s long run extreme risk on A’s long run conditional volatility, we X = B_qpgarch_t, Y = A_pgarch_t. In other words, 1) and 2) test the influence of extreme risks with long and short run volatility components on each other’s corresponding conditional volatility respectively.

3. Empirical Results and Analysis

Regarding that what we discuss is the leading relationship between Shanghai composite index and 9 international indices, we have 18 groups of causality test for every volatility indicator. Table 1 and Table 2 report the P-value corresponding to F-statistic in Granger causality test. The results less than 5% are displayed with the

bold face. X => Y means that the null hypothesis is that X does not Granger-cause Y. The bold face therefore reveals that we can refuse the hypothesis at the possibility of 5% with the given lagged values，from which we can conclude that X can Granger-cause Y.

From the tables above we can figure out that the interconnections between variables are identified stably in tests with longer lag phases. For example, in the test for qtgarch indicator of Table 2, the influence from shortrun extreme risk of FTSE index on Shanghai index can be identified when the lag value is greater than 5. It means that there is hysteresis effect in the relationship between volatilities and it is important to choose longer lag length for the test. In addition, a number of tests have revealed that the leading relationship which is significant in the short run will vanish in the long run. For instance, in the inspection about the influence from GDAXI index on Shanghai index (Table 1), the early test indicates that Shanghai A-share index has an effect on GDAXI index, while the leading relation disappears when the lag value is greater than 25. In that case, the leading relationship which seems to exist between Shanghai index and oversea indices in the short run can be explained by the past information of the oversea indices. As a result, the leading relationship is confirmed to exist when it is significant in test with longer lag length. The tests satisfying such standard are signified by “^**” to show that this pair of tests has a leading relationship.

In the first place, we will observe the spillover effect of the extreme risk of Shanghai index on the overseas market. Table 1 shows that the extreme risk of Shanghai index will have an influence on all of the oversea indices observed in this paper from the perspective of long run volatility. On the other hand, Table 2 demonstrates that the extreme risk of Shanghai index has few effects on oversea indices in the view of short run volatility, except for influencing the American DJI index.

Then we will observe the spillover effect of the extreme risk of overseas market on Shanghai index. Table 1 shows that in light of long run volatility, only the extreme risks from Australian market and Japan market will

have spillover effects on the extreme risk of Shanghai index. The short run volatility (in Table 2) reveals that extreme risks of AORD index, DJI index, and FTSE index have spillover effects on the extreme risk of Shanghai index.

In conclusion, Table 1 and Table 2 demonstrate that there is spillover effect of extreme risks in the long run volatility of Chinese stock market. In term of the short run volatility, there is spillover effect from the extreme risks of overseas stock markets on the extreme risk of Chinese stock market. On account that the long-run volatility components are more related to real economic cycle, the results to some extent reflects the profound influence of China’s economy on the world economy.

4. Conclusion

This paper analyzed the interconnection between Shanghai index and main international stock indices with the CGARCH Model and Granger Causality Test. With regards to the perspective of volatility among markets, we attach importance to influence of extreme risk on the distribution of conditional volatility. Consequently, we choose the long and short run volatility components of stock index returns and their corresponding extreme risk events. We also test the spillover effect between Shanghai index and 9 international indices.

The results show that, the influence of China’s stock market on international stock markets is different from short run and long run perspectives. Under the circumstance of long run volatility components, the extreme risk of China’s stock market has an effect on all of the oversea indices chosen in this paper. On the contrary, China’s stock market is influenced by oversea indices respect to short run volatility. We thus believe that the A share market has the power to influence the volatility of international stock markets. Because long run volatility is closer to the real economic cycle, our results reflect the profound influence of China’s economy on the international economy from the perspective of extreme risk spill over.

Another realistic problem related to this study is the regulation for stock index futures. The offering of stock index future products provides speculators with more speculative tools. Apart from the speculative trading, the more important factors accounting for the volatility of stock index futures are the volatility of benchmark stock index itself and the speculative arbitrage operations caused by the change of market expectation. One of the important resources for the volatility of domestic index is the volatility of external markets. Such volatility is mainly due to the short run disturbance and may not reflect the change of economic cycle, which is only “noise”. As a result, the domestic regulatory authorities and the investors should seriously treat the unreasonable disturbance from oversea markets.

Acknowledgements

This paper is funded by the Projects of National Natural Science Foundation (No. 71003094).

References