American Journal of Climate Change
Vol.03 No.03(2014), Article ID:49927,16 pages
10.4236/ajcc.2014.33026
Trend and Periodicity of Temperature Time Series in Ontario
Syed Imran Ahmed1*, Ramesh Rudra1, Trevor Dickinson2, Motahir Ahmed2
1School of Engineering, Thornborough Building, University of Guelph, Guelph, Canada
2Engineer, Manitoba Government, Winnipeg, Canada
Email: *sahmed@uoguelph.ca
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 8 June 2014; revised 5 July 2014; accepted 1 August 2014
ABSTRACT
The trends and periodicities in the annual and seasonal temperature time series at fifteen weather stations within Ontario Great Lakes Basins have been analyzed, for the period 1941-2005, using the statistical analyses (Fourier series analysis, t-test, and Mann-Kendall test). The stations were spatially divided into three regions: northwest (NW), southwest (SW), and southeast (SE) to eva- luate spatial variability in temperature. The results of the study reveal that the annual maximum mean temperature showed increasing trend for NW, and mixed trends for SW and SE regions. The variability was found to be more for northern stations as compared to southern stations for an- nual extreme minimum temperature. In addition, the trend slope per 100 years for the average annual extreme minimum temperature increased within the range of −0.8˚C (Stratford) to 15˚C (Porcupine). The seasonal analysis demonstrated that extreme maximum temperature has an in- creasing trend and maximum mean temperature has a decreasing trend during summer and win- ter. The extreme minimum temperature for winter illustrated an increasing trend (90%) with 22% statistically significant for NW region. For the SW region, the trend is also increasing (80%) for most of the temperature variables and 25% of temperature data were significantly increased in the SW region. The SE region stations showed overall very clear increasing trends (95%) for all the temperature variables. The data also showed that 47% of data were statistically significant in the SE region. The analysis of variance accounted for by trend, significant periodicities, and ran- dom component show that the pattern is similar for the percent of variance accounted for peri- odicities, and random component contribute dominantly for the four temperature variables and frost free days (FFD) for all three regions. Overall, the study reveals that the extreme minimum temperature is increasing annually and seasonally, with statistically significant at many stations.
Keywords:
Time Series, Trend, Periodicity, Mann-Kendall Test, t-Test, Frost Free Days

1. Introduction
Evaluation of weather indicators has been of pivotal consideration to many researchers since the past century. The apprehension lies in the climatic effects being global or local. Generally, these studies are performed to as- sess climatic variables (precipitation and temperature) on a watershed, an area that is physiographically varying. Improved understanding of these changes, spatially and temporally, is essential to understand the current and future climate change. The effect of climate change could result in the frequency and severity of extreme weath- er events including short duration/high intensity rainfalls and temporal distribution of temperature. United States Environmental Protection Agency (USEPA) (2013) report states that since 1901, the global average surface temperature has risen at an average rate of 0.13˚F per decade (or 1.3˚F per century) [1] . Analysis of meteorologi- cal parameters has been carried out across the globe by many researchers, and eventually these findings have been used by policy makers and planners of relevant areas for future designing work and disaster management practices.
Time series analysis has immense importance in hydrology for the last few decades. It has been carried out for various hydrological components such as rainfall data analysis [2] [3] , and stream flow analysis [4] -[8] . Recent- ly, these temporal analyses have been used to evaluate the change in climatic conditions using rainfall and tem- perature data [4] [9] -[11] . Trends and periodicities are usually present in hydrological time series if a significant correlation exists between the observations and time.
The trend and periodicity analysis of temperature time series is of great importance because of the effects of global climate change, and most time series patterns can be described by trend and seasonality. Trend ideally comprises consistently increasing or decreasing (i.e. monotonous) data. The trends in a time series, either linear or non-linear, qualitatively assess the possible existence and type of the trends. Many studies have been con- ducted for detecting climatic trends in the past. Air temperature and precipitation data (1949 to 1989) were in- vestigated using the Mann-Kendall (MK) test for monotonic trends for Canada and north-eastern USA. It found that western Canada has experienced significant warming effect in January and March and to a limited extent in April, May, and June, but virtually no warming trend was detected in eastern Canada and north-eastern USA. The author also found some cooling trends, particularly in October [12] .
The rank-based nonparametric Mann-Kendall test (MK) [13] [14] is widely used to assess the significance of monotonic trends in hydrometeorological time series [12] [15] -[20] . The power of the parametric t-test, non- parametric MK, and bootstrap-based MK (BS-MK) tests has been assessed to detect linear and non-linear trends in both normal and non-normal time series. It was concluded that these may be used to assess the significance of trends on normally-distributed series; however, rank-based tests were recommended for non-normal series [21] .
Marcov Chain Monte Carlo (MCMC) simulation technique has also been used by the researchers to assess the significance of monotonic trends [21] and to predict a longer time series [22] . Periodicity and trend for multisite daily rainfall time series and developed simulation criteria was modeled to obtain a longer time series [22] . There are several procedures of periodicity estimation such as spectral analysis [23] [24] , auto-regressive mov- ing average method [25] [28] , and simple harmonic analysis [29] -[32] .
Although several studies on temperature trend have been conducted in Canada, very few of them demonstrate periodicity components with respect to Ontario conditions. The main objective of this study was to evaluate the trends and periodicities of various temperature variables (extreme maximum, extreme minimum, and mean) on annual and seasonal time series for the selected stations in southern Ontario.
2. Materials and Methods
2.1. Description of Data
The choice for the climatic stations was based on spatial coverage across Ontario and availability of the reliable historical climatic data over the longest possible period. Climatologists use historical data to compare current climatological trends to that of the past or what is considered as normal trend, which is on the arithmetic average of a climate element (e.g. temperature) over a 30-year period. A 30-year period is considered as long enough to sreen out any annual anomalies. However, longer than 30 years of data is recommended for climatic trends. Since it is not appropriate to analyze temperature trend in subinterval shorter than 30 years, data available for all the selected stations are longer than 30 years.
For this analysis, 15 stations were selected from all over Ontario. The fifteen selected stations were further divided into three regions, Northwest (NW), Southwest (SW), and Southeast (SE), according to their location in the province. Figure 1 shows the climatic stations. Every region has five stations. The SE and SW stations were considered as east and west of Toronto, respectively. The NW region consists of Kenora, Sioux Lookout, Thunder Bay, Sault Ste. Marie, and Porcupine. The SW has Windsor, London, Stratford, Owen Sounds, and Fergus; and SE region has Pearson, Orillia, Belleville, Kingston, and Ottawa. The list of the selected stations along with other related information is given in Table 1.
The temperature variable in this study, monthly maximum, monthly minimum, and monthly mean tempera- ture data correspond to the maximum, minimum, and mean of the daily data, respectively, at the study stations (Figure 1). Similarly, annual maximum, minimum, and mean data correspond to the maximum, minimum, and mean values, respectively, within a year. The mean data have further been divided into maximum mean and minimum mean series. The maximum mean corresponds to the maximum value of the daily mean values and the minimum mean corresponds to the minimum of the daily mean values recorded in a year. The annual series has also been divided into two seasonal series, such as winter (November through April) and summer (May through October), in order to investigate the seasonal variations of the temperature extremes and the means. The season- al maximum and minimum values correspond to the maximum and minimum temperatures recorded in a season.
2.2. Analyses
The analysis of temperature data used in this study (Table 1) showed that some data were missing at Sault Ste Marie, Porcupine, Orillia, and Kingston. The missing data at these three stations have been ignored or disre- garded in the analysis. Therefore, the present analysis is based on the available data for the possible maximum period for these stations. Time series data for the rest of the stations vary between 60 to 65 years. However, the trend lines correspond to a continuous line with no break points.
The statistical analyses consist of least square method and moving averages to observe the potential trends on the individual series. The periodicity analysis has been performed on the de-trended (residuals) series using Fourier series transformation. The harmonic cycles which significantly contributed to the structure of the time
Figure 1. Study area and locations of all the stations for temperature analysis.
Table 1. Data used for analysis for fifteen stations in the study.
series were determined by inspecting the correlogram showing lag autocorrelation. The correlogram depicts the autocorrelation between two sets of data versus the lag time in the scale of year. In this study the starting year for the individual station has been taken into account as a base year for autocorrelation function. The numbers of significant harmonics those fit the time series have been extracted from the correlogram for each tempera- ture variables. The significant harmonics, the outliers beyond the confidence limits set in the correlogram, have been applied in the Fourier series transformation to observe the periodicities in the time series. Also, student’s t-test and Mann-Kendall test have been employed to determine the significance of any trends in the data series [14] .
The frost free days (FFD) in a year have been recognized as the days having temperatures greater than 0˚C. The trend lines on annual frost free days for all stations were evaluated, and the t-test results for slope of the trend lines drawn onto the annual frost free days were also analyzed.
2.3. Time Series Analysis
2.3.1. Time Series Components
A time series is expressed as a function of three components such as trend, seasonality, and randomness. A hy- drological time series is considered to be stationary if it is homogeneous and trend-free. The simple model for time series may be expressed as:
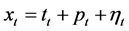 (1)
(1)
where 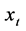 represents the observed value of the variable at time
represents the observed value of the variable at time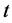 ,
,  and
and 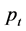 are the trend and periodicity components, respectively, and
are the trend and periodicity components, respectively, and 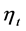 is a random or stochastic component.
is a random or stochastic component.
In this study, the stochastic component has been disregarded and only trend and periodicity components have been taken into account. In principle, trend component is treated as a simple linear regression process and the periodicity component represents sum of sine and cosine functions.
2.3.2. Trend and Periodicity
The regression methods are applicable to time series data to estimate linear trends with time. Linear trend esti- mates are useful for studying various types of climate change parameters, including air temperature [32] . The following steps have been used for the trend and periodicity analysis:
1) Fit the least square line on the raw data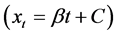 , where
, where 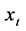 is the series value at time
is the series value at time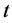 . The slope of the regression line
. The slope of the regression line 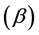 is estimated by the linear regression technique. The slope determines the characte- ristics of the trend.
is estimated by the linear regression technique. The slope determines the characte- ristics of the trend.
2) Subtract the least square line from the raw data in order to remove the trend from the original data yielding residuals, using equation: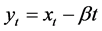 , where
, where  is the de-trended series.
is the de-trended series.
3) Plot the residuals, 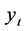 against time
against time 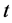 (yr).
(yr).
4) Fit the de-trended series, using the following Equation (2) in order to examine the periodicity in the de- trended time series [28] :

where



To find a reasonable periodic structure, significant harmonics are determined from the correlogram and 
Correlogram showing the autocorrelation coefficients at different lags of time for several years has been es- tablished to determine the significant harmonics contributing to the time series of the residuals. To obtain the correlogram for each set of data, consecutive lag-one serial correlation co-efficient 

where
The lag-one correlation test shows a statistical significance of serial correlation patterns. The correlogram showing the harmonic processes should comply with the oscillatory movement of the non-random series. The shape of the correlogram indicates the generation of autoregressive process of the time series.
2.3.3. Hypothesis Test (t-Test) for Slope of Regression Line
Parametric or non-parametric tests are useful to detect whether there is statistically significant trend in the data. In this study, a parametric student’s 
To determine whether there is a significant linear relationship between an independent variable 


where 





The null hypothesis states that the slope is equal to zero, and the alternative hypothesis states that the slope is not equal to zero. The standard procedures for 
2.3.4. Mann-Kendall (MK) Test
A non-parametric MK test has also been used to test the significance either increasing, decreasing or no signifi- cant trend present in the temperature series in this study. The MK test shows whether the trends are significant or non-significant with respect to increase or decrease in temperature over the period of study. The MK rank sta- tistic is considered to be the most appropriate for the analysis of trends in climatological time series [34] . MK rank statistic requires the following equations to test the significance of the trend [35] :



where 



The following equations are also proposed for MK test [36] :

where 




Increasing or decreasing trend can be identified depending on the value of


3. Results and Discussion
3.1. Annual Temperature Trend Using MK Test
Increasing or decreasing of temperature over the period in linear scale determines the trend. A linear trend is a monotonic trend having a constant change rate, and is useful to approximate the trends in time series analysis. In this study, the best-fit linear trend is drawn onto the annual data available for the stations to detect any significant changes in temperature (data not shown). Table 2 presents the annual temperature trends for all fifteen stations in three regions for four temperature variables considered in the analysis. These data show that annual extreme minimum temperature increased for all the stations except for Stratford. However, the increase in annual extreme minimum temperature for SE region was statistically significant. The trend is also increasing for annual
Table 2. Annual temperature trends for all fifteen stations for the study.
‡Increasing trend; †Statistically significant; ±Decreasing trend.
minimum mean temperature for most of the stations in three regions. Overall, 76% of annual minimum tempera- ture data showed an increasing trend and approximately 23% were statistically significant trends.
The annual maximum mean temperature also showed increasing trend for Northwest region, and mixed trends for southwest and southeast regions (Table 2). Interestingly the analysis for annual extreme maximum tempera- ture showed mostly decreasing or no trends for all the stations. Overall, the annual maximum temperatures showed 40% increasing and 37% decreasing trend when averaged over the fifteen stations.
Overall, 75%, 35%, and 70% of temperature data showed increasing trend, and 10%, 40%, and 25% data showed decreasing trend in temperature for northwest, southwest, and southeast regions, respectively, indicating spatial variability of temperature among stations across Ontario. The analysis by combining and averaging all the temperature data for fifteen stations showed an overall 60% increasing and 17% statistically significant trends (Table 2). In addition, 25% of the data showed decreasing trend and 15% of the data showed no trend.
To further evaluate the spatial variability in temperature, the trend line slopes for change in temperature for all the stations for each variable (1 = Extreme minimum; 2 = Minimum Mean; 3 = Extreme maximum, and 4 = Maximum mean) are shown in Figure 2. The data show the smaller variability in maximum temperatures among the stations, and the larger variability for minimum temperatures. The larger variability is visible for northwest stations as compared to southwest and southeast stations for annual extreme minimum temperature (Figure 2). The range of change in annual extreme minimum temperature is −0.8˚C/100 years at Stratford to 15˚C/100 years at Porcupine. It is important to mention that Porcupine has the least amount of temperature data available for analysis which might have influenced the results. The range of change in minimum mean temperature over 100 years, 0.7˚C to 9.8˚C, is smaller than change in annual extreme minimum temperature. The mean values for minimum temperatures for all three regions also show more variability as compared to mean values for maxi- mum temperatures for all the stations (data not shown). This trend is also clear from the plot of medians for all
Figure 2. Annual trend slopes and their medians for four temperature va- riables for the studied stations in Ontario.
three regions as shown in Figure 2. The trend of the medians for all three regions also show that slope for the southwest region is flatter than the slopes for the other two regions, depicting less variability in deviation of all temperatures variables in southwest region.
The trend slope for the annual extreme maximum temperature showed smaller change with flatter slope fluc- tuating between ±2.1˚C. The maximum annual mean temperature showed less variability ranging between −1.1˚C to 2.7˚C (Figure 2). Again, the smaller range of variability in temperature shows less variation for maxi- mum temperatures.
The results of this analysis were also compared with the previous studies [35] -[37] . The trends for various temperature variables in the present study are found to be similar or relatively larger than those observed in the previous studies. It has been reported that the annual mean temperature has increased by about 2˚C in western Canada over 48 years (1950-1998), while a slight cooling trend occurred in the north-east [36] . It was also re- ported 1.8˚C increase in annual mean maximum temperature over 84 years period at Mont Joli, Quebec [37] . Temperature trend between 1961-2004 at Norman Wells in Northwest Territories were analyzed, a warming area in Canada and found that the annual mean temperature has increased by 2˚C over 44-year period [38] .
3.2. Seasonal Temperature Trend Using MK Test
The seasonality in temperature time series is represented by the seasonal variation of temperature trends. The analysis of seasonal variations in temperature was conducted by splitting the annual time series into two seasonal series, winter and summer as described in the previous section. The seasonal trends of temperature variables for all the stations are shown in Table 3.
The winter temperature analysis shows an increasing trend for all the temperature variables for three regions (Table 3). These data show 90% positive trends and 22% significant positive trends for northwest stations. For this region only Sault Ste. Marie and Porcupine showed a non-significant decreasing trend for maximum mean tempera- ture, and the positive trend for extreme minimum temperature was statistically significant at three stations.
For the southwest region, 80% of trends are positive for most of the temperature variables except minimum mean temperature which depicted mix trends. Only 25% of the trends showed significant increase in the tempera- ture data for this region. The stations in the southeast region clearly reveal an increasing trend (95%) for all the temperature variables, particularly for extreme minimum and maximum mean temperatures with 47% significant trends. The overall analysis of the winter data shows 83% increasing trends with 32% significant trends.
Figure 3 illustrates more regional variability of the winter extreme minimum and minimum mean tempera-
Figure 3. Winter trend slopes and their medians for four temperature va- riables for the studied stations in Ontario.
Table 3. Winter temperature trends for all fifteen stations for the study.
tures among all stations. However, the variability in extreme maximum temperature during winter was found to be the least for these stations. The slopes of the medians for all three regions were found to be different. The northwest stations show larger variability for extreme minimum (0˚C - 15˚C/100 years) and minimum mean temperature (1.3˚C - 9.4˚C/100 years), with median values of 4.8˚C/100 years and 5˚C/100 years, respectively. For winter season median values of minimum mean and extreme maximum temperature were similar for all three regions. However, the median values for southeast region (4˚C/100 years) and southwest region (4.9˚C/100 years) indicates a significant larger increase in maximum mean temperature as compared to the northwest region (0.9˚C/100 years).
The summer temperature trends for three regions for four temperature variables for all fifteen stations are shown in Table 4. The magnitude of change in trend for the extreme minimum and minimum mean tempera- tures for northwest region is similar to annual temperature trends (Table 2). However, the summer extreme maximum and maximum mean temperatures trend are opposite in sign to the annual trends for these variables (Table 2 and Table 4). The extreme maximum temperature shows an increasing trend and maximum mean temperature showed a decreasing trend during summer (Table 4).
The results for summer temperatures in Table 4 also show that 70% of the stations in the northwest region have increasing trend with 36% statistically significant region. For the southwest region the data show 60% in- creasing trend, 42% significant and 25% decreasing trend. The southeast region stations also showed clear in- creasing trends (75%) for all the temperature variables except for the extreme maximum temperature. The over- all analysis of summer data, averaging across three regions, showed 68% increasing trend, and 18% decreasing trend with 54% statistically significant.
The comparison of the summer and annual temperature data showed similar trends for SW region except ex- treme minimum temperature which showed statistically significant increase in extreme minimum temperature.
Table 4. Summer temperature trends for all fifteen stations for the study.
‡Increasing trend; †Statistically significant; ±Decreasing trend; ¥No trend.
The extreme minimum and minimum mean temperatures trends were found to be similar for SE region for summer and annual time periods. However, the summer extreme maximum and maximum mean temperatures reveal opposite trends when compared with the annual trends for the stations in the southeast region.
The trend slopes and their medians for four temperature variables for the studied stations are presented in Figure 4. These data show spatially more variability in extreme minimum temperature among the stations, and less variability for other temperature variables for the summer period. The highest variability was found for northwest stations as compared to southwest and southeast stations. In addition, the trend slope per 100 years for the average summer extreme minimum temperature varied from 1.4˚C (Thunder Bay) to 9.8˚C (Porcupine) in the northwest region. The pattern for minimum mean temperature was similar with a range of 0.2˚C to 4.3˚C. The trend slopes for the mean temperature for all three regions show similar variability for other three tempera- ture variables. In addition, this trend is also clear from plotting the medians for all three regions (Figure 4). However, the medians of all four variables for three regions show that slope for the NW region is flatter than the slopes for the SW and SE regions. Add some discussion about the variability in the variable.
3.3. Trend, Periodicities, and Random Components
The periodicities fitted on the de-trended series show the periodic fluctuations in temperature after the trend component has been removed from the data. The fitted residuals show that periodicities are more sporadic in case of minimum temperature and the periodic fluctuations are relatively higher. This has been observed possi- bly due to the higher variability in the data range. The figures showing periodic lines are not included in this paper for brevity. However, the percentage of variance contributed by trend, significant periodicity, and random components for the annual and seasonal series are shown in Tables 5-7.
The variance accounted for by the random or stochastic components has been calculated by subtracting the variance accounted for by trend and periodicity components from the total variance. The mean values for the percentage of variance for trend for the extreme maximum, maximum mean, and minimum mean temperatures for all three regions are very similar (Table 5); however, mean extreme minimum temperature values were rela- tively higher for NW (6.89%) and SE (6.30%) regions than the SW (1.48) region. The data in Table 5 also show that the pattern is similar for the percent of variance accounted by periodicity for all four temperature variables for stations in all three regions. However, the effect of periodicity was less for maximum mean temperature
Figure 4. Summer trend slopes and their medians for four temperature va- riables for the studied stations in Ontario.
Table 5. Percentage of variance accounted for trend, periodicities, and randomness for annual time series.
†Extreme Maximum Temperature; ‡Maximum Mean Temperature; ±Minimum Mean Temperature; ≠Extreme Minimum Temperature; πFrost Free Days.
comparative to other temperature variables. The stochastic or random component dominated the contribution to the variance for all the four temperature variables in the time series (Table 5).
The analysis of trend lines on annual frost free days for all stations and the t-test results for slope of the trend lines showed upward trend of the least square line for the annual frost free days with time for almost every sta- tion (Table 6). The slopes of the trend lines at Porcupine, Windsor, London, and Kingston are found to be stee- per than the other locations. The number of frost free days is relatively greater in Windsor than other stations. On the other hand, the number of frost free days at Thunder Bay and Sioux Lookout are observed less and the slopes of the trend lines are milder. The t-test result shows that the slopes of the trend lines of frost free days for Sioux Lookout and Thunder Bay stations are insignificant (Table 6). The other stations show significant trends. It is evident that the number of frost free days is increasing due to increase in mean winter temperature as well as increase in the annual extreme minimum temperatures.
Table 7 presents the relative contribution to the variance by trend, periodicity, and randomness components for four temperature variable for summer season. The contribution by trend to the variance for extreme mini- mum temperature for three regions is relatively higher when compared with the rest of the temperature variables.
Table 6. p-values from t-test on slopes of annual and seasonal temperature trend lines.
†Significant at 5% level of significance.
The contribution of periodicity to the variance is highest for extreme minimum temperature for the southwest and southeast regions. The stations in the northwest region showed mixed pattern of the contribution of peri- odicity to the total variance for four temperature variables. Summer temperature analysis also showed that ran- dom effect is dominant contributor to the variation of temperature variables.
The contribution by trend, periodicity and random components to variance for the winter temperature for all stations is shown in Table 8. These data indicate that the trend effects are the largest contributor to the variance in the extreme minimum temperature for the northwest and southeast regions. For the southwest region the trend effect was the highest for maximum mean temperature. The periodic effects are relatively dominant for maxi- mum and minimum means temperature for all stations. The magnitude of the random component contributions to the variance of the temperature variables is similar to the contributions for the annual and summer tempera- ture variables.
4. Conclusions
The trends and periodicities of annual and seasonal temperatures at fifteen selected stations in Ontario Great Lakes Basins, for the period 1941-2005, were investigated using statistical analysis. The stations were divided in three regions and four temperature variables, extreme minimum, minimum mean, extreme maximum, maximum mean, were considered for this study. The following conclusions are drawn from the study:
The analysis of annual temperature trends show that annual extreme minimum temperature increased for all the stations except for Stratford. In addition, the increase in annual extreme minimum temperature for SE re- gion was statistically significant. The trend is also increasing for annual minimum mean temperature for most of the stations. The analysis for annual extreme maximum temperature showed mostly decreasing or no trend for all the stations. However, the annual maximum mean showed increasing trend for NW, and mixed trends for SW, and SE regions. Overall, 75%, 35%, and 70% data showed increasing trend, and 10%, 40%, and 25% data showed decreasing trend in temperature for NW, SW, and SE regions, respectively. Rest of the data showed no specific trends in temperature variables considered for this study.
Table 7. Percentage of variance accounted for trend, periodicities, and randomness for summer time series.
†Extreme Maximum Temperature; ‡Maximum Mean Temperature; ±Minimum Mean Temperature; ≠Extreme Minimum Temperature.
Data showed lesser variability in annual maximum temperatures among the stations, and the higher variabil- ity for minimum temperatures. The highest variability was found for northern stations as compared to south- ern stations for annual extreme minimum temperature. In addition, the trend slope per 100 years for the av- erage annual extreme minimum temperature increased within the range of −0.8˚C (Stratford) to 15˚C (Por- cupine).
The seasonal analysis demonstrated that extreme maximum temperature has an increasing trend and maxi- mum mean temperature has a decreasing trend during summer for NW region. The summer trends were op- posite to the annual trends for these variables. The summer and annual temperature trends were similar for SW region except extreme minimum which showed statistically significant increase in extreme minimum temperature. The summer extreme maximum and maximum mean temperatures illustrated opposite trends when compared with the annual trends for the stations in the SE region. In addition, the highest variability was found for NW stations as compared to SW and SE stations for summer period.
The extreme minimum temperature for winter illustrated an increasing trend (90%) with 22% statistically significant NW for NW region. For the SW region, the trend is also increasing (80%) for most of the tem- perature variables and 25% of temperature data were significantly increased in the SW region. The SE re-
Table 8. Percentage of variance accounted for trend, periodicities, and randomness for winter time series.
†Extreme Maximum Temperature; ‡Maximum Mean Temperature; ±Minimum Mean Temperature; ≠Extreme Minimum Temperature.
gion stations showed overall very clear increasing trends (95%) for all the temperature variables. The data also showed that 47% of data were statistically significant in the SE region. The FFD results show that the slopes of the trend lines of frost free days for most of the stations are significant. It is evident that the num- ber of frost free days is increasing due to increase in mean winter temperature as well as increase in the an- nual extreme minimum temperatures.
The analysis of variance accounted for by trend, significant periodicities, and random component show that the pattern is similar for the percent of variance accounted for periodicities for all four temperature variables for stations in all three regions. The percent of variance accounted for stochastic or random component con- tribute dominantly in the time series of the four temperature variables. The data shows more periodicity for maximum temperatures than the minimum temperatures.
Overall, the study reveals that the extreme minimum temperature is increasing annually and seasonally, with statistically significant at many stations in Ontario, Canada. Also, annual and summer extreme maximum tem- perature is decreasing significantly.
References
- US Environmental Protection Agency (2013) Temperature. http://www.epa.gov/climatechange/science/indicators/weather-climate/temperature.html
- Mirza, M.Q., Warrick, R.A., Ericksen, N.J. and Kenny, G.J. (1998) Trends and Persistence in Precipitation in the Ganges, Brahmaputra and Meghna River Basins. Hydrological Sciences Journal, 43, 845-858. http://dx.doi.org/10.1080/02626669809492182
- Astel, A., Mazerski, J., Polkowska, Z. and Namiesnik, J. (2004) Application of PCA and Time Series Analysis in Stu- dies of Precipitation in Tricity (Poland). Advances in Environmental Research, 8, 337-349. http://dx.doi.org/10.1016/S1093-0191(02)00107-7
- Costain, J.K. and Bollinger, G.A. (1996) Climatic Changes, Streamflow, and Long-Term Forecasting of Intraplate Seismicity. Journal of Geodynamics, 22, 97-117.
- Milhous, R.T. (2003) Mixing Physical Habitat and Streamflow Time Series Analysis. Colorado State University, Of- fice of Conference Services, Fort Collins, 21 p.
- Yildirim, Y.E., Turkes, M. and Tekiner, M. (2004) Time-Series Analysis of Long-Term Variations in Stream-Flow Data of Some Stream-Flow Stations over the Gediz Basin and in Precipitation of the Akhisar Station. Pakistan Journal of Biological Sciences, 7, 17-24. http://dx.doi.org/10.3923/pjbs.2004.17.24
- Chen, C.S., Liu, C.H. and Su, H.C. (2008) A Nonlinear Time Series Analysis Using Two-Stage Genetic Algorithms for Streamflow Forecasting. Hydrological Processes, 22, 3697-3711. http://dx.doi.org/10.1002/hyp.6973
- Shao, Q., Wong, H., Li, M. and Ip, W.C. (2009) Streamflow Forecasting Using Functional-Coefficient Time Series Model with Periodic Variation. Journal of Hydrology, 368, 88-95. http://dx.doi.org/10.1016/j.jhydrol.2009.01.029
- Kite, G. (1989) Use of Time Series Analyses to Detect Climatic Change. Journal of Hydrology, 111, 259-279. http://dx.doi.org/10.1016/0022-1694(89)90264-3
- Khan, A.R. (2001) Analysis of Hydro-Mateorological Time Series in the Upper Indus Basin: Searching Evidence for Climatic Change. International Water Management Institute, Working Paper 23, Pakistan Country Series Number 7, Colombo.
- Bani-Domi, M. (2005) Trend Analysis of Temperatures and Precipitation in Jordan. Umm Al-Qura University Journal of Educational, Social Sciences & Humanities, 17, 1-36.
- Gan, T.Y. (2007) Trends in Air Temperature and Precipitation for Canada and North-Eastern USA. International Jour- nal of Climatology, 15, 1115-1134. http://dx.doi.org/10.1002/joc.3370151005
- Mann, H.B. (1945) Non-Parametric Tests against Trend. Econometrica, 13, 245-259.
- Kendall, M.G. (1975) Rank Correlation Measures. Charles Griffin, London.
- ven Belle, G. and Hughes, J.P. (1984) Nonparametric Tests for Trend in Water Quality. Water Resources Research, 20, 127-136.
- Cailas, M.D., Cavadias, G. and Gehr, R. (1986) Application of a Nonparametric Approach for Monitoring and Detecting Trends in Water Quality Data of the St. Lawrence River. Water Pollution Research Journal of Canada, 21, 153- 167.
- Hipel, K.W., McLeod, A.I. and Weiler, R.R. (1988) Data Analysis of Water Quality Time Series in Lake Erie. JAWRA: Journal of the American Water Resources Association, 24, 533-544. http://dx.doi.org/10.1111/j.1752-1688.1988.tb00903.x
- Chiew, F.H.S. and McMohan, T.A. (1993) Detection of Trend or Change in Annual Flow of Australian Rivers. International Journal of Climatology, 13, 643-653. http://dx.doi.org/10.1002/joc.3370130605
- Yue, S., Pilon, P.J., and Phinney, B. (2003) Canadian Streamflow Trend Detection: Impacts of Serial and Cross-Cor- relation. Hydrological Sciences Journal, 48, 51-63. http://dx.doi.org/10.1623/hysj.48.1.51.43478
- Feidas, H., Makrogiannis, T. and Bora-Senta, E. (2004) Trend Analysis of Air Temperature Time Series in Greece and Their Relationship with Circulation Using Surface and Satellite Data: 1955-2001. Theoretical and Applied Climatology, 79, 185-208. http://dx.doi.org/10.1007/s00704-004-0064-5
- Yue, S. and Pilon, P. (2004) A Comparison of the Power of the t Test, Mann-Kendall and Bootstrap Tests for Trend Detection. Hydrological Sciences Journal, 49, 21-37. http://dx.doi.org/10.1623/hysj.49.1.21.53996
- Kottegoda, N.T., Natale, L. and Raiteri, E. (2008) Stochastic Modelling of Periodicity and Trend for Multisite Daily Rainfall Simulation. Journal of Hydrology, 361, 319-329. http://dx.doi.org/10.1016/j.jhydrol.2008.08.008
- Burg, J.P. (1967) Maximum Entropy Spectral Analysis. Proceedings of 37th Meeting, Society of Exploration Geophysics, Oklahoma City.
- Marple, L. (1980) A New Autoregressive Spectrum Analysis Algorithm. IEEE Transactions on Acoustics, Speech and Signal Processing, 28, 441-454.
- Cadzow, J.A. (1981) Autoregressive Moving Average Spectral Estimation: A Model Equation Error Procedure. IEEE Transactions on Geoscience and Remote Sensing, 19, 24-28. http://dx.doi.org/10.1109/TGRS.1981.350324
- Friedlander, B. (1982) A Recursive Maximum Likelihood Algorithm for ARMA Spectral Estimation. IEEE Transactions on Information Theory, 28, 639-646. http://dx.doi.org/10.1109/TIT.1982.1056531
- Friedlander, B. (1982) Systematic Identification Technique for Adaptive Signal Processing. Circuits, Systems and Signal Processing, 1, 3-41. http://dx.doi.org/10.1007/BF01600032
- Kay, S.M. and Marple, S.L. (1981) Spectrum Analysis: A Modern Perspective. Proceedings of the Institute of Electrical and Electronic Engineering, 69, 1380-1419.
- Rao, A.R., Jeong, G.D. and Chang, F.J. (1992) Estimation of Periodicities in Hydrological Data. Stochastic Hydrology and Hydraulics, 6, 270-288. http://dx.doi.org/10.1007/BF01581621
- Chen, Z., Grasby, S.E., and Osadetz, K.G. (2004) Relation between Climate Variability and Groundwater Levels in the Upper Carbonate Aquifer, Southern Manitoba, Canada. Journal of Hydrology, 290, 43-62. http://dx.doi.org/10.1016/j.jhydrol.2003.11.029
- Omidvari, M., Hassanzadeh, S. and Hosseinibalam, F. (2007) Time Series Analysis of Ozone Data in Isfahan. Journal of Physics A, 387, 4393-4403.
- Easterling, D.R., Horton, B., Jones, P.D., Peterson, T.C., Karl, T.R., Parker, D.E., Salinger, M.J., Razuvayev, V., Plummer, N., Jamason, P. and Folland, C.K. (1997) Maximum and Minimum Temperature Trends for the Globe. Sci- ence, 277, 364-367. http://dx.doi.org/10.1126/science.277.5324.364
- Machiwal, D. and Jha, M.K. (2008) Comparative Evaluation of Statistical Tests for Time Series Analysis: Application to Hydrological Time Series. Hydrological Sciences Journal, 53, 353-366. http://dx.doi.org/10.1623/hysj.53.2.353
- Goosens, C. and Berger, A. (1986) Annual and Seasonal Climatic Variations over the Northern Hemisphere and Europe during the Last Century. Annales Geophysicae, Series B, 4, 385-400.
- Onoz, B. and Bayazit, M. (2003) The Power of Statistical Tests for Trend Detection. Turkish Journal of Engineering and Environmental Sciences, 27, 247-251.
- Sneyers, R. (1990) On the Statistical Analysis of Series of Observations. Technical Note No. 143, WMO No. 415, World Meteorological Organization, Geneva, 192 p.
- Zhang, X., Vincent, L., Hogg, W.D. and Niitsoo, A. (2000) Temperature and Precipitation Trends in Canada during the 20th Century. Atmosphere-Ocean, 38, 395-429. http://dx.doi.org/10.1080/07055900.2000.9649654
- Vincent, L.A., Zhang, X., Bonsal, B.R. and Hogg, W.D. (2002) Homogenization of Daily Temperatures over Canada. Journal of Climate, 15, 1322-1334. http://dx.doi.org/10.1175/1520-0442(2002)015<1322:HODTOC>2.0.CO;2
NOTES
*Corresponding author.








