International Journal of Modern Nonlinear Theory and Application
Vol.05 No.01(2016), Article ID:64244,8 pages
10.4236/ijmnta.2016.51004
Controlling Liu Chaotic System with Feedback Method and Its Circuit Realization
Mingjun Wang
School of Information Engineering, Dalian University, Dalian, China

Copyright © 2016 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 15 October 2015; accepted 4 March 2016; published 7 March 2016
ABSTRACT
In the paper, the Liu system with a feedback controller is discussed. The influence of the feedback coefficient of the controlled system is studied through Lyapunov exponents spectrum and bifurcation diagram. Various attractors are demonstrated not only by numerical simulations but also by circuit experiments. Only one feedback channel is used in our study, which is useful in communication. The circuit experiments show that our study has significance in practical applications.
Keywords:
Liu System, Chaotic Circuit, Chaotic Control, Circuit Realization

1. Introduction
In 1990, Ott, Grebogi and Yorke presented the OGY method to control chaos [1] . After their pioneering work, chaotic control has become a focus in nonlinear problems and a lot of work has been done in the field [2] - [4] . Nowadays, many methods have been proposed to control chaos [5] [6] . Generally speaking, there are two kinds of control ways: feedback control and nonfeedback control. Feedback methods [7] - [11] are used to stabilize the unstable periodic orbit of chaotic systems by feeding back their states. Nonfeedback methods [11] -[14] are adopted to change chaotic behaviors by applying perturbations to some parameters or variables. In the paper, we use feedback method to control the dynamic behavior of Liu system. By adjusting feedback coefficient, Liu system can be stabilized at equilibrium point or limit cycle around its equilibrium. Lyapunov exponents spectrum and bifurcation diagram are adopted to analyze the dynamic behavior of the controlled system. Numerical simulations and circuit experiments show the effectiveness of this method.
2. The Description of Liu System
Liu system [15] is described as
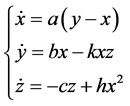 (1)
(1)
When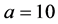 ,
, 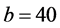 ,
, 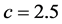 ,
, 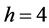 and
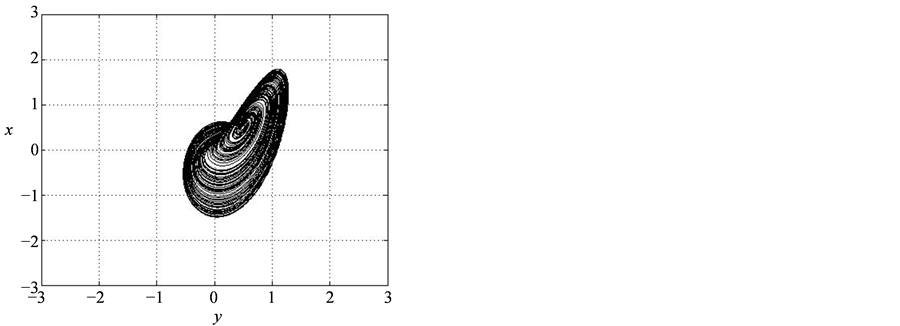
and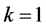 , system (1) exhibits a chaotic behavior. Its attractor is shown in Figure 1. The projections of system (1)’s attractor are shown in Figure 2. System (1) has three equilibriums:
, system (1) exhibits a chaotic behavior. Its attractor is shown in Figure 1. The projections of system (1)’s attractor are shown in Figure 2. System (1) has three equilibriums: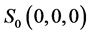 ,
, 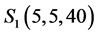 ,
,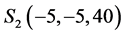 .
.
Considering the voltage restraint of practical electronic components, let
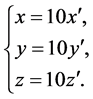 (2)
(2)
Then in the new coordinate system, system (1) will be described as
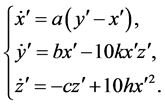 (3)
(3)
System (3) can be seemed as a reduced Liu system and the equilibriums are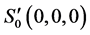 ,
, 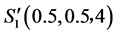 ,
,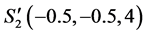 . The circuit realization of Equation (3) is shown in Figure 3.
. The circuit realization of Equation (3) is shown in Figure 3.
In Figure 3, the voltages of C1, C2, C3 are used as variables. The relevant function can be described as
Figure 1. The chaotic attractor of Liu system.
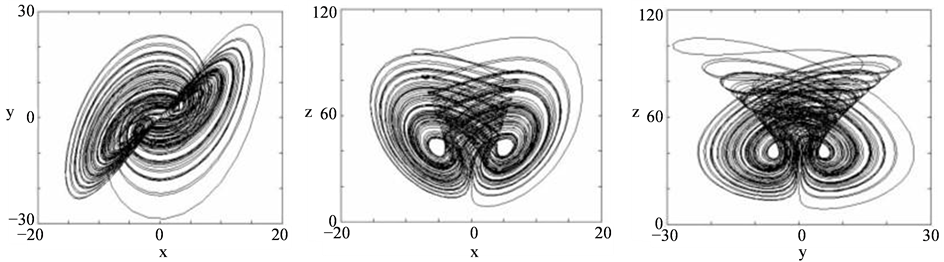
Figure 2. The projections of Liu attractor.
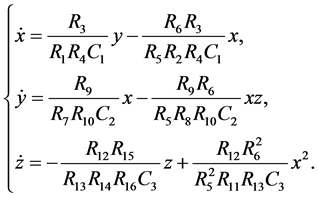
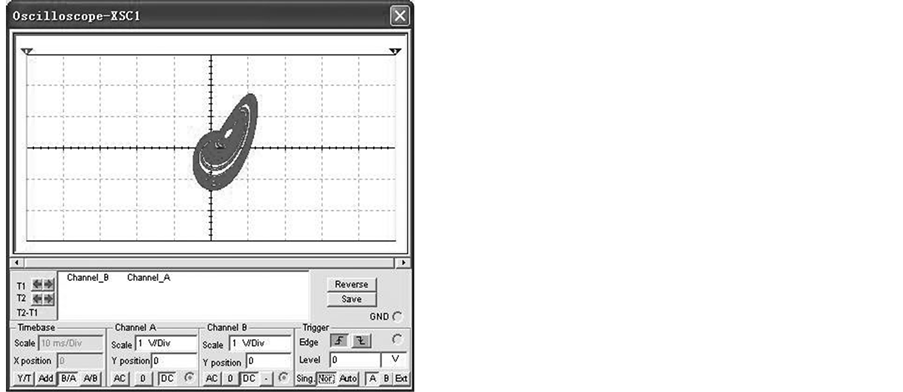
When we choose R1 = 10 kΩ, R2 = 20 kΩ, R3 = 10 kΩ, R4 = 100 kΩ, R5 = 10 kΩ, R6 = 20 kΩ, R7 = 10 kΩ, R8 = 80 kΩ, R9 = 40 kΩ, R10 = 100 kΩ, R11 = 10 kΩ, R12 = 10 kΩ, R13 = 100 kΩ, R14 = 10 kΩ, R15 = 10 kΩ, R16 = 40 kΩ, C1 = C2 = C3 = 1 μF, the circuit system (4) is equivalent to system (3). The supplies of all active devices are ±18 V and the initial voltages of C1, C2, C3 are random, we obtain the experiment observations of system (4) as Figure 4 (with Multisim 7.0).
Figure 3. Circuit diagram for system (3).
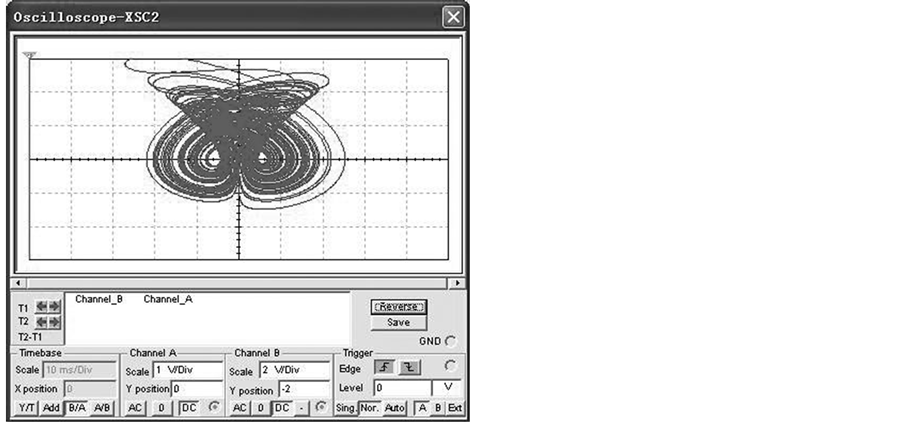
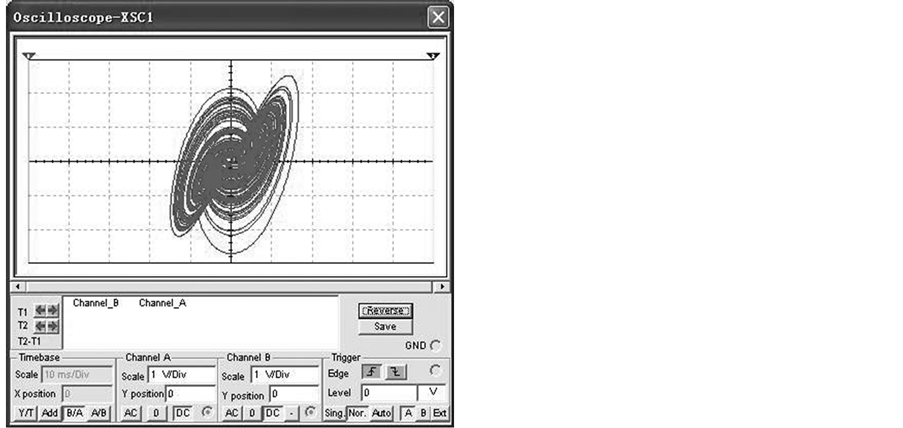
Figure 4. The experiment observations of system (4). (a) x-y plane; (b) y-z plane.
Comparing Figure 2 and Figure 4, we can know that a reduced Liu system has been realized by circuit experiment. Next, we will add a feedback controller to this circuit to control chaos. Various attractors will be demonstrated not only by numerical simulations but also by the circuit experiment observations.
3. Feedback Control of Liu System
Suppose we want to stabilize Liu system at equilibrium 

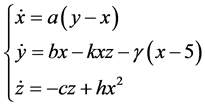
where 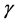
In order to study the relation between 
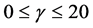
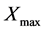

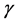
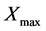


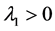
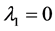


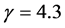

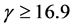
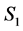
We obtain the above conclusions by numerical calculation. In fact, the accurate range for 

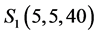
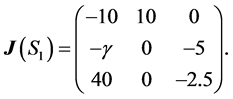
Suppose 

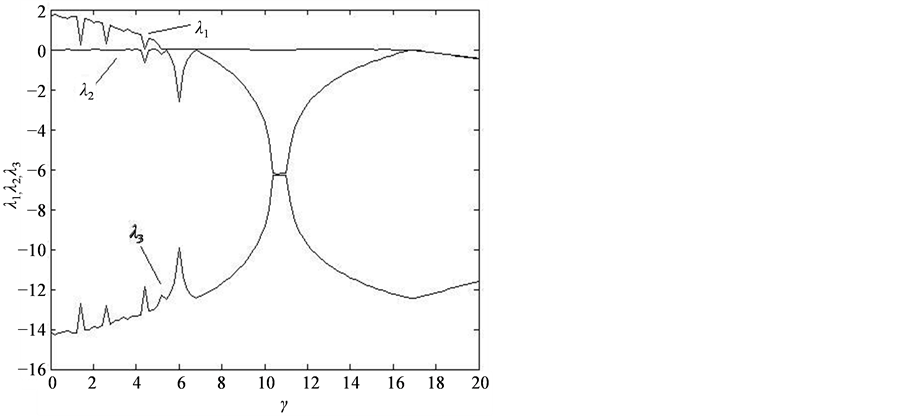
Figure 5. Bifurcation diagram of system (5).
Figure 6. Lyapunov exponents spectrum of system (5).
where

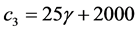
According to Routh-Hurwitz criterion, when



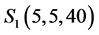
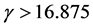
4. Numerical Simulations and Circuit Realization
As for the reduced Liu system, it’s easy to obtain the relevant controlled system:
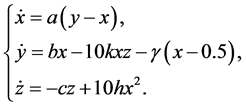
Obviously the above conclusions about 
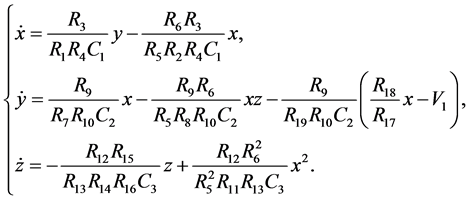
When we choose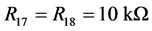
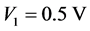

Substitute the value of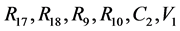

Choose typical value 

Figure 7. Circuit diagram for system (8).
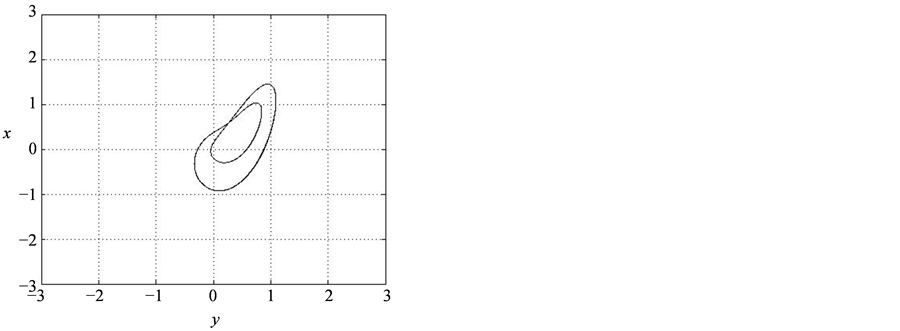

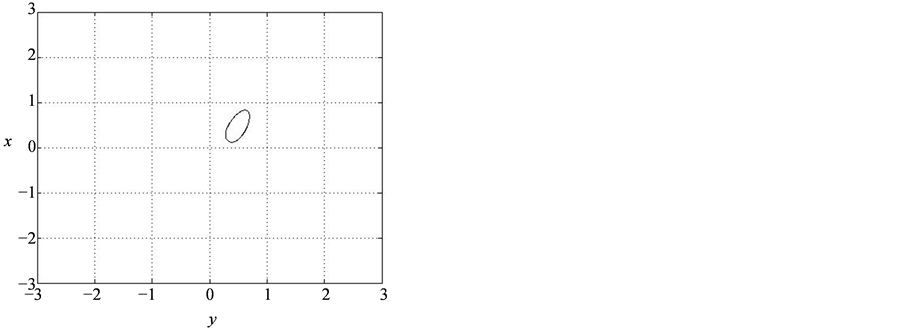
Figure 8. The simulation results of system (8). (a)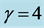

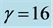
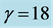

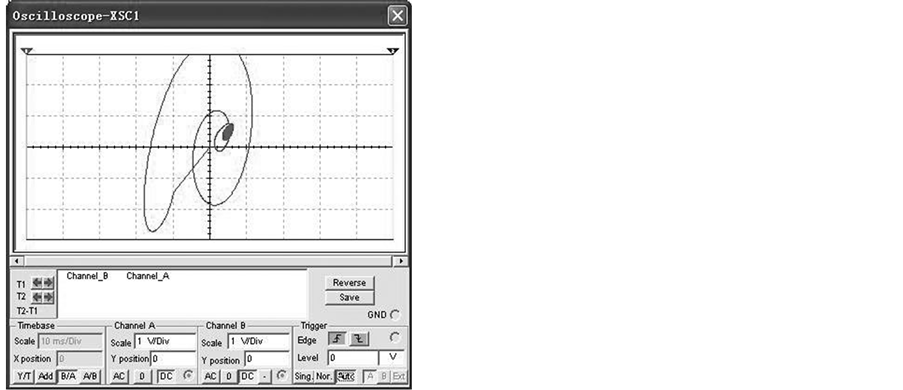
Figure 9. The experiment observations of system (9). (a)



From Figure 8 and Figure 9, we can know that system (8) is equivalent to system (9) in troth. When 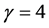
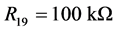
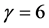

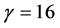

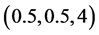

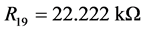
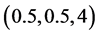
5. Conclusion
We study the chaotic control of Liu system with feedback method in the paper. Liu chaotic system and its control are realized not only by numerical simulations but also by circuit experiments. Computer simulation and circuit experiment results show the effectiveness of our method. Moreover, our control needs only one communication channel, which is significant in practical applications.
Acknowledgements
The work was supported by Doctor Specific Funds of Dalian University.
Cite this paper
MingjunWang, (2016) Controlling Liu Chaotic System with Feedback Method and Its Circuit Realization. International Journal of Modern Nonlinear Theory and Application,05,40-47. doi: 10.4236/ijmnta.2016.51004
References
- 1. Ott, E., Grebogi, C. and Yorke, J.A. (1990) Controlling Chaos. Physical Review Letters, 64, 1196-1199.
http://dx.doi.org/10.1103/PhysRevLett.64.1196 - 2. Chen, G. and Dong, X. (1998) From Chaos to Order: Methodologies, Perspectives and Applications. World Scientific, Singapore.
http://dx.doi.org/10.1142/3033 - 3. Wang, G.R., Yu, X.L. and Chen, S.G. (2001) Chaotic Control, Synchronization and Utilizing. National Defence Industry Press, Beijing.
- 4. Guan, X.P., Fan, Z.P., Chen, C.L. and Hua, C.C. (2002) Chaotic Control and Its Application on Secure Communication. National Defence Industry Press, Beijing.
- 5. Chen, G.R. and Lü, J.H. (2003) Dynamical Analyses, Control and Synchronization of the Lorenz System Family. Science Press, Beijing.
- 6. Wang, X.Y. (2003) Chaos in the Complex Nonlinearity System. Electronics Industry Press, Beijing.
- 7. Jang, M.J., Chen, C.L. and Chen, C.K. (2002) Sliding Mode Control of Hyperchaos in Rossler Systems. Chaos, Solitons & Fractals, 14, 1465-1476.
http://dx.doi.org/10.1016/S0960-0779(02)00084-X - 8. Ghosh, D., Saha, P. and Chowdhury, A.R. (2010) Linear Observer Based Projective Synchronization in Delay Rossler System. Communications in Nonlinear Science and Numerical Simulation, 15, 1640-1647.
http://dx.doi.org/10.1016/j.cnsns.2009.06.019 - 9. Zheng, Y.A. (2006) Controlling Chaos Using Takagi-Sugeno Fuzzy Model and Adaptive Adjustment. Chinese Physics, 15, 2549-2552.
http://dx.doi.org/10.1088/1009-1963/15/11/015 - 10. Gong, L.H. (2005) Study of Chaos Control Based on Adaptive Pulse Perturbation. Acta Physica Sinaca, 54, 3502-3507.
- 11. Roopaei, M., Sahraei, B.R. and Lin, T.C. (2010) Adaptive Sliding Mode Control in a Novel Class of Chaotic Systems. Communications in Nonlinear Science and Numerical Simulation, 15, 4158-4170.
http://dx.doi.org/10.1016/j.cnsns.2010.02.017 - 12. Paula, A.S. and Savi, M.A. (2011) Comparative Analysis of Chaos Control Methods: A Mechanical System Case Study. International Journal of Non-Linear Mechanics, 46, 1076-1089.
http://dx.doi.org/10.1016/j.ijnonlinmec.2011.04.031 - 13. Dadras, S. and Momeni, H.R. (2010) Adaptive Sliding Mode Control of Chaotic Dynamical Systems with Application to Synchronization. Mathematics and Computers in Simulation, 80, 2245-2257.
http://dx.doi.org/10.1016/j.matcom.2010.04.005 - 14. Wu, Z.M., Xie, J.Y., Fang, Y.Y. and Xu, Z.Y. (2007) Controlling Chaos with Periodic Parametric Perturbations in Lorenz System. Chaos, Solitons & Fractals, 32, 104-112.
http://dx.doi.org/10.1016/j.chaos.2005.10.060 - 15. Liu, C.X., Liu, T., Liu, L. and Liu, K. (2004) A New Chaotic Attractor. Chaos, Solitons & Fractals, 22, 1031-1038.
http://dx.doi.org/10.1016/j.chaos.2004.02.060 - 16. Ramasubramanian, K. and Sriram, M.S. (2000) A Comparative Study of Computation of Lyapunov Spectra with Different Algorithms. Physica D, 139, 72-86.
http://dx.doi.org/10.1016/S0167-2789(99)00234-1