International Journal of Modern Nonlinear Theory and Application
Vol.04 No.02(2015), Article ID:57352,10 pages
10.4236/ijmnta.2015.42010
The Global Attractors for a Nonlinear Viscoelastic Wave Equation with Strong Damping and Linear Damping and Source Terms
Liang Guo, Zhaoqin Yuan, Guoguang Lin
Department of Mathematics, Yunnan University, Kunming, China
Email: guoliang142857@163.com, yuanzq091@163.com, gglin@ynu.edu.cn
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 20 April 2015; accepted 19 June 2015; published 24 June 2015
ABSTRACT
In this paper, firstly, some priori estimates are obtained for the existence and uniqueness of solutions of a nonlinear viscoelastic wave equation with strong damping, linear damping and source terms. Then we study the global attractors of the equation.
Keywords:
Global Attractors, Viscoelastic Equation, Priori Estimates

1. Introduction
We know that viscoelastic materials have memory effects. These properties are due to the mechanical response influenced by the history of the materials. As these materials have a wide application in the natural science, their dynamics are of great importance and interest. The memory effects can be modeled by a partial differential equation. In recent years, the behaviors of solutions for the PDE system have been studied extensively, and many achievements have been obtained. Many authors have focused on the problem of existence, decay and blow-up for the last two decades, see [1] -[5] . And the attractors are still important contents that are studied.
In [6] , R.O. Araújo, T. Ma and Y.M. Qin studied the following equation
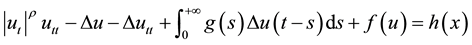 (1.1)
(1.1)
and they proved the global existence, uniqueness and exponential stability of solutions and existence of the global attractor.
In [7] , Y.M. Qin, B.W. Feng and M. Zhang considered the following initial-boundary value problem:
 (1.2)
(1.2)
where 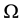 is a bounded domain of
is a bounded domain of 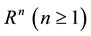 with a smooth boundary
with a smooth boundary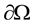 ,
, 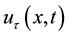 (the past history of u) is a given datum which has to be known for all
(the past history of u) is a given datum which has to be known for all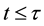 , the function g represents the kernel of a memory,
, the function g represents the kernel of a memory, 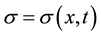
is a non-autonomous term, called a symbol, and ρ is a real number such that 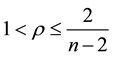 if
if ;
; 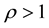 if
if
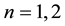 . They proved the existence of uniform attractors for a non-autonomous viscoelastic equation with a past history. For more related results, we refer the reader to [8] -[14] .
. They proved the existence of uniform attractors for a non-autonomous viscoelastic equation with a past history. For more related results, we refer the reader to [8] -[14] .
In this work, we intend to study the following initial-boundary problem:
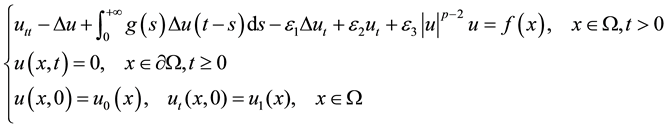 (1.3)
(1.3)
where  and
and 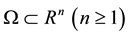 is a bounded domain with smooth boundary
is a bounded domain with smooth boundary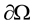 ,
,







near damping term 

A direct computation yields
Thus, the original memory term can be written as
and we get a new system


with the initial conditions

and the boundary conditions

The rest of this paper is organized as follows. In Section 2, we first obtain the priori estimates, then in Section 3, we prove the existence of the global attractors.
For convenience, we denote the norm and scalar product in 




2. The Priori Estimates of Solution of Equation
In this section, we present some materials needed in the proof of our results, state a global existence result, and prove our main result. For this reason, we assume that
(G1) 

(G2)
(G3) There exists a constant 


Lemma 1. Assume (G1), (G2) and (G3) hold, let
and





here



Proof. We multiply 
By using Holder inequality, Young’s inequality and Poincare inequality, we get

and

and

For the first term on the right side (2.5), by using (G1), (G2) and (G3), we have

where

For the second term on the right side (2.5), by using Holder inequality and Young’s inequality, we get

So, we have

By using Poincare inequality, we obtain

and

and

By using Holder inequality and Young’s inequality, we obtain

Then, we have

That is

Next, we take proper

Taking

where

From


Then
So, there exists 

Lemma 2. Assume (G1), (G2) and (G3) hold, let
and





Here



Proof. We multiply 

By using Holder inequality, Young’s inequality and Poincare inequality, we get
and

and

For the first term on the right side (2.23), by using (G1), (G2) and (G3), we have

where

For the second term on the right side (2.23), by using Holder inequality and Young’s inequality, we get

so, we have
By using Poincare inequality, we have

and

And using Interpolation Theorem, we have

By using Holder inequality and Young’s inequality, we have

Then, we have
That is

Next, we take proper

Taking

where

From


then
So, there exists 

3. Global Attractors
Theorem 1. Assume (G1), (G2) and (G3) hold, let
and


Proof. By the method of Galerkin and Lemma 1 and Lemma 2, we can easily obtain the existence of solutions. Next, we prove the uniqueness of solutions in detail.
Assume that 


where

By multiplying the equation by 


here

and

by using (G1), (G2) and (G3), we have

By using Poincare inequality, we have

and

By using Holder inequality, Young’s inequality and Poincare inequality, we have

then, we have

That is

Taking

By using Gronwall inequality, we have

So we get
Theorem 2. Let X be a Banach space, and 




1) 



2) It exists a bounded absorbing set


3) When

Therefore, the semigroup operators 
Theorem 3. Under the assume of Theorem 1, equations have global attractor
where


1)

2)

Proof. Under the conditions of Theorem 1, it exists the solution semigroup


1) From Lemma 1 to Lemma 2, we can get that 
the ball
This shows that 

2) Furthermore, for any

So, we get 
3) Since 



So, the semigroup operators 
Acknowledgements
The authors express their sincere thanks to the anonymous reviewer for his/her careful reading of the paper, giving valuable comments and suggestions. These contributions greatly improved the paper.
Funding
This work is supported by the National Natural Sciences Foundation of People’s Republic of China under Grant 11161057.
References
- Messaoudi, S.A. (2003) Blow Up and Global Existence in a Nonlinear Viscoelastic Wave Equation. Mathematische Nachrichten, 260, 58-66. http://dx.doi.org/10.1002/mana.200310104
- Cavalcanti, M.M., Domingos Cavalcanti, V.N. and Ferreira, J. (2001) Existence and Uniform Decay for Nonlinear Viscoelastic Equation with Strong Damping. Mathematical Methods in the Applied Sciences, 24, 1043-1053. http://dx.doi.org/10.1002/mma.250
- Berrimi, S. and Messaoudi, S.A. (2006) Existence and Decay of Solutions of a Viscoelastic Equation with a Nonlinear Source. Nonlinear Analysis: Theory, Methods & Applications, 64, 2314-2331. http://dx.doi.org/10.1016/j.na.2005.08.015
- Lu, L.Q. and Li, S.J. (2011) Cauchy Problem for a Nonlinear Viscoelastic Equation with Nonlinear Damping and Source Term. Applied Mathematics Letters, 24, 1275-1281. http://dx.doi.org/10.1016/j.aml.2011.01.009
- Kafini, M. and Mustafa, M.I. (2014) Blow-Up Result in a Cauchy Viscoelastic Problem with Strong Damping and Dispersive. Nonlinear Analysis: Real World Applications, 20, 14-20. http://dx.doi.org/10.1016/j.nonrwa.2014.04.005
- Araújo, R.O., Ma, T. and Qin, Y.M. (2013) Long-Time Behavior of a Quasilinear Viscoelastic Equation with Past History. Journal of Differential Equations, 254, 4066-4087. http://dx.doi.org/10.1016/j.jde.2013.02.010
- Qin, Y.M., Feng, B.W. and Zhang, M. (2014) Uniform Attractors for a Non-Autonomous Viscoelastic Equation with a Past History. Nonlinear Analysis: Theory, Methods & Applications, 101, 1-15. http://dx.doi.org/10.1016/j.na.2014.01.006
- Qin, Y.M., Zhang, J.P. and Sun, L.L. (2013) Upper Semicontinuity of Pull Back Attractors for a Non-Autonomous Viscoelastic Equation. Applied Mathematics and Computation, 223, 362-376. http://dx.doi.org/10.1016/j.amc.2013.08.034
- Conti, M. and Geredell, P.G. (2015) Existence of Smooth Global Attractors for Nonlinear Viscoelastic Equations with Memory. Journal of Evolution Equations. http://dx.doi.org/10.1007/s00028-014-0270-2
- Cavalcanti, M.M., Domingos Cavalcanti, V.N., Prates Filho, J.A. and Soriano, J.A. (2001) Existence and Uniform Decay Rates for Viscoelastic Problems with Non-Linear Boundary Damping. Differential and Integral Equations, 14, 85- 116.
- Muñoz Rivera, J.E., Lapa, E.C. and Barreto, R. (1996) Decay Rates for Viscoelastic Plates with Memory. Journal of Elasticity, 44, 61-87. http://dx.doi.org/10.1007/BF00042192
- Wu, S.T. (2011) General Decay of Solutions for a Viscoelastic Equation with Nonlinear Damping and Source Terms. Acta Mathematica Scientia, 31, 1436-1448. http://dx.doi.org/10.1016/S0252-9602(11)60329-9
- Ma, T.F. and Narciso, V. (2010) Global Attractor for a Model of Extensible Beam with Nonlinear Damping and Source Terms. Nonlinear Analysis: Theory, Methods & Applications, 73, 3402-3412. http://dx.doi.org/10.1016/j.na.2010.07.023
- Qin, Y., Deng, S. and Schulze, W. (2009) Uniform Compact Attractors for a Nonlinear Non-Autonomous Equation of Viscoelasticity. Journal of Partial Differential Equations, 22, 153-198.
























