International Journal of Modern Nonlinear Theory and Application
Vol.03 No.02(2014), Article ID:46903,8 pages
10.4236/ijmnta.2014.32007
On the Generalization of Integrator and Integral Control Action
Baishun Liu
Academy of Naval Submarine, Qingdao, China
Email: baishunliu@163.com
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 16 April 2014; revised 16 May 2014; accepted 23 May 2014
ABSTRACT
This paper provides a solution to generalize the integrator and the integral control action. It is achieved by defining two function sets to generalize the integrator and the integral control action, respectively, resorting to a stabilizing controller and adopting Lyapunov method to analyze the stability of the closed-loop system. By originating a powerful Lyapunov function, a universal theorem to ensure regionally as well as semi-globally asymptotic stability is established by some bounded information. Consequently, the justification of two propositions on the generalization of integrator and integral control action is verified. Moreover, the conditions used to define the function sets can be viewed as a class of sufficient conditions to design the integrator and the integral control action, respectively.
Keywords:
General Integral Control, Nonlinear Control, General Integrator, General Integral Action, Sufficient Condition, Lyapunov Function, Output Regulation

1. Introduction
Integral control [1] plays an important role in control system design because it ensures asymptotic tracking and disturbance rejection. In general, integral controller comprises three components: the stabilizing controller, the integral control action and the integrator. In the presence of the parametric uncertainties and the unknown constant disturbances, the stabilizing controller is used to guarantee the stability of the closed-loop system, and the integrator and the integral control action are utilized to create a steady-state control action at the equilibrium point such that the tracking error is zero. This shows that the integrator and the integral control action are two indispensable components to design an integral controller. Therefore, it is of important significance to generalize the integrator and the integral control action such that for a particular application, the engineers can choose the most appropriate integrator and integral control action to design their own integral controller. As a result, it also leads to a challenging trouble because the stability of the closed-loop system depends on not only the uncertain parameters and the unknown disturbances but also the general integrator and integral control action.
1.1. Traditional Integrator and Integral Control Action
Before the idea of general integral control appeared, all of the integrators were called the traditional integrator. Thus, traditional integrators can be classified into four kinds of integrators: 1) the simplest integrator, which is achieved by integrating the error; 2) the conditional integrator [2] -[7] , in which the integrator value is frozen or restricted when certain conditions are verified; 3) the back-calculation integrator [8] -[11] , in which the difference between the controller output and the actual plant input is fed back to the integrator; 4) the nonlinear integrator [12] -[16] , whose output is shaped by a nonlinear error function before it enters the integrator. In addition, a class of special conditional integrator was proposed by [7] , in which the integrator was shaped by integrating the linear combination of the error and its derivative, but its value can be changed only inside the boundary layer. All these integrators, except for the one proposed by [7] , were designed by using the error as the indispensable element. All these traditional integral control actions are almost shaped by multiplying the output of the integrator by a gain coefficient.
1.2. General Integrator and Integral Control Action
In 2009, the idea of general integral control, which uses all available state variables to design the integrator, was proposed by [17] , where presented some linear and nonlinear general integrators. However, their justification was not proved by strictly mathematical analysis. In 2012, the rationality of the linear integrator [18] on all the states of the system was proved by using linear system theory. The results, however, were local. The regionally as well as semi-globally results were proposed in [19] , where the sliding mode manifold was used as the integrator, and then general integral control design was achieved by using sliding mode technique and linear system theory. In 2013, based on feedback linearization technique, a class of nonlinear integrator, which was shaped by a linear combination of the diffeomorphism, was presented by [20] . General concave function gain integrator was proposed in [21] , where the partial derivative of Lyapunov function was introduced into the integrator. General convex function gain integrator was presented in [22] , where a systematic method to construct the convex function gain integrator, whose output is bounded in time domain, was proposed. Except for general convex and concave integral control, all the general integral control actions above are shaped by multiplying the output of the integrator by a gain coefficient. However, the integral control actions of general convex and concave integral control are generalized by two function sets, respectively, and the indispensable element used to design the concave and convex function gain integrators is only extended to the partial derivative of Lyapunov function.
All these integrators along with the integral control actions above constitute only a minute portion of the integrators and the integral control actions, and therefore lack generalization. Moreover, in consideration of the complexity of nonlinear system, it is clear that we cannot expect that a particular integrator or a particular integral control action has the high control performance for all nonlinear system. For these reasons above, the generalization of the integrator and the integral control action appears naturally because for all nonlinear system, we cannot enumerate all the categories of the integrators and the integral control actions with high control performance. It is not hard to know that this is a very valuable and challenging problem and the new theorem could be needed to solve this trouble.
Motivated by the cognition above, the aim of this paper is to generalize the integrator and the integral control action such that for a particular application, the engineers can choose the most appropriate stabilizing controller, integrator and integral control action to design their own integral controller. The main contributions are as follows: 1) two function sets, which are used to generalize the integrator and the integral control action, respectively, are defined; 2) the integrator can be taken as any integrable function, which passes through the origin and whose partial derivative, induced by mean value theorem, is positive-define and bounded. Moreover, the conditions on the function above can be viewed as a class of sufficient conditions to design an integrator; 3) the integral control action can be taken as any continuous differential increasing function with the positive-define bounded derivative. Moreover, the conditions on the function above can be viewed as a class of sufficient conditions to design the integral control action; 4) by originating a powerful Lyapunov function, a universal theorem to ensure regionally as well as semi-globally asymptotic stability is established by some bounded information. Consequently, the justification of two propositions on the generalization of the integrator and the integral control action is verified. Moreover, Lyapunov function proposed here has an important significant, and even could lay the foundation of the stability analysis of the complex nonlinear system with general integral control.
Throughout this paper, we use the notation 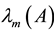 and
and 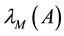 to indicate the smallest and the largest eigenvalues, respectively, of a symmetric positive-define bounded matrix
to indicate the smallest and the largest eigenvalues, respectively, of a symmetric positive-define bounded matrix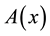 , for any
, for any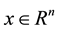 . The norm of
. The norm of
vector x is defined as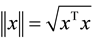 , and that of matrix A is defined as the corresponding induced norm
, and that of matrix A is defined as the corresponding induced norm .
.
The remainder of the paper is organized as follows: Section 2 describes the system under consideration, assumption and definition; Section 3 addresses the method to generalize the integrator and the integral control action. Conclusions are presented in Section 4.
2. Problem Formulation
Consider the following nonlinear system,
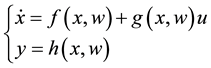 (1)
(1)
where 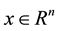 is the state,
is the state, 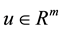 is the control input,
is the control input, 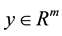 is the controlled output,
is the controlled output, 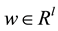 is a vector of unknown constant parameters and disturbance. The function f, g and h are continuous in
is a vector of unknown constant parameters and disturbance. The function f, g and h are continuous in 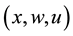 on the control domain
on the control domain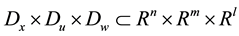 . In this study, the function
. In this study, the function 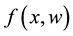 does not necessarily vanish at the origin; i.e.,
does not necessarily vanish at the origin; i.e.,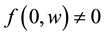 . Let
. Let 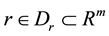 be a vector of constant reference. Set
be a vector of constant reference. Set 



Assumption 1: For each



so that 



For convenience, we state all definitions, assumptions and theorems for the case when the equilibrium point is at the origin of

Assumption 2: No loss of generality, suppose that the function 


for all 


Assumption 3: Suppose there is a control law 



and there exists a Lyapunov function 



hold for all






Definition 1: 







where 
Figure 1 depicts the example curves of one component of the functions belonging to the function set





Definition 2: 





where z is a point on the line segment connecting x to the origin.
Figure 2 depicts the example curves of one component of the functions belonging to the function set






and so on, all belong to the function set
Discussion 1: The condition for Definition 2 is induced by mean value theorem. It seems to be difficulty to construct such a multivariable function, in fact, it can be designed by the following method: for each component of










and so on.
3. Generalization Method
In general, integral controller comprises three components: the stabilizing controller, the integral control action and the integrator. Therefore, for achieving the generalization of the integral control action and the integrator, we resort to the control law 
Figure 1. Example curves of one component of the functions belonging to the function set
Figure 2. Example curves of one component of the functions belonging to the function set

where 




Thus, substituting (10) into (1), obtain the augmented system,

By Assumption 1 and choosing 



Therefore, we ensure that there is a unique solution


Now, the design task is to provide the conditions on the control parameters such that 


Theorem 1: Under Assumptions 1 - 3, if there exists a positive-define diagonal matrix 

and the inequality (20) hold, and then 
Proof: To carry out the stability analysis, we consider the following Lyapunov function candidate,

where











Obviously, Lyapunov function candidate (14) is positive-define. Therefore, our task is to show that its time derivative along the trajectories of the closed-loop system (11) is negative define, which is given by,

By using (12), the closed-loop system (11) can be rewritten as,

By Definition 2, we have,
and then, using Definition 1, obtain,

Substituting (16) into (15), and using (3), (4), (5), (8), (9) and (16), we have,

where


and

and then inequality (17) can be rewritten as,

where

The right-hand side of the inequality (18) is a quadratic form, which is negative define when,

Using the fact that Lyapunov function (14) is a positive-define function and its time derivative is a negative define function if the inequalities (13) and (20) hold, we conclude that the closed-loop system (11) is stable. In fact, 


Discussion 2: Although Theorem 1 is proved by resorting to a stabilizing controller 



Proposition 1: The integrator can be taken as any integrable function, which passes through the origin and whose partial derivative, induced by mean value theorem, is positive-define and bounded. Moreover, the conditions on the function above can be viewed as a class of sufficient conditions to design an integrator.
Proposition 2: The integral control action can be taken as any continuous differential increasing function with the positive-define bounded derivative. Moreover, the conditions on the function above can be viewed as a class of sufficient conditions to design an integral control action.
Discussion 3: Compared with the integrators and the integral control actions proposed by [1] -[23] , it is obvious that: 1) the integrator is not confined to the several forms and can be taken any function, which belongs to the function set



Discussion 4: From the stability analysis procedure above, it is obvious that: 1) Lyapunov function plays the most key role in the stability analysis because it is the start point and the foundation of Lyapunov method; 2) just Lyapunov function (14) is founded, and then the theorem to ensure regionally as well as semiglobally asymptotic stability is established. Therefore, two propositions can be verified; 3) just the time derivatives of Lyapunov function (14) can be transformed into a quadratic form, and then the very tedious trouble, that is, how deal with the coupling terms on x and
4. Conclusions
In consideration of the complexity of nonlinear system, this paper provided a solution to generalize the integrator and the integral control action such that for a particular application, the engineers can choose the most appropriate stabilizing controller, integrator and integral control action to design their own integral controller. The main contributions are as follows: 1) two function sets, which are used to generalize the integrator and the integral control action, respectively, are defined; 2) the integrator can be taken as any integrable function, which passes through the origin and whose partial derivative, induced by mean value theorem, is positive-define and bounded. Moreover, the conditions on the function above can be viewed as a class of sufficient conditions to design an integrator; 3) the integral control action can be taken as any continuous differential increasing function with the positive-define bounded derivative. Moreover, the conditions on the function above can be viewed as a class of sufficient conditions to design the integral control action; 4) by originating a powerful Lyapunov function, a universal theorem to ensure regionally as well as semi-globally asymptotic stability is established by some bounded information. Consequently, the justification of two propositions on the generalization of the integrator and the integral control action is verified. Moreover, Lyapunov function proposed here has an important significant, and even could lay the foundation of the stability analysis of the complex nonlinear system with general integral control.
References
- Khalil, H.K. (2000) Universal Integral Controllers for Minimum-Phase Nonlinear Systems. IEEE Transactions on Automatic Control, 45, 490-494. http://dx.doi.org/10.1109/9.847730
- Krikelis, N.J. and Barkas, S.K. (1984) Design of Tracking Systems Subject to Actuator Saturation and Integrator Windup. International Journal of Control, 39, 667-682. http://dx.doi.org/10.1080/00207178408933196
- Hanus, R., Kinnaert, M. and Henrotte, J.L. (1987) Conditioning Technique, a General Anti-Windup and Bumpless Transfer Method. Automatica, 23, 729-739. http://dx.doi.org/10.1016/0005-1098(87)90029-X
- Peng, Y., Varanceic, D. and Hanus, R. (1996) Anti-Windup, Bumpless, and Conditioned Transfer Techniques for PID Controllers. IEEE Control Systems Magazine, 16, 48-57. http://dx.doi.org/10.1109/37.526915
- Cao, Y.Y., Lin, Z.L. and David, G.W. (2004) Anti-Windup Design of Output Tracking Systems Subject to Actuator Saturation and Constant Disturbances. Automatica, 40, 1221-1228. http://dx.doi.org/10.1016/j.automatica.2004.02.012
- Marchand, N. and Hably, A. (2005) Global Stabilization of Multiple Integrators with Bounded Controls. Automatica, 41, 2147-2152. http://dx.doi.org/10.1016/j.automatica.2005.07.004
- Seshagiri, S. and Khalil, H.K. (2005) Robust Output Feedback Regulation of Minimum-Phase Nonlinear Systems Using Conditional Integrators. Automatica, 41, 43-54.
- Åstrom, K.J. and Rundquist, L. (1989) Integrator Windup and How to Avoid It. Proceedings of the 1989 American Control Conference, Pittsburgh, 21-23 June 1989, 1693-1698.
- Shahruz, S.M. and Schwartz, A.L. (1994) Design and Optimal Tuning of Nonlinear PI Compensators. Journal of Optimization Theory and Applications, 83, 181-198. http://dx.doi.org/10.1007/BF02191768
- Hodel, A.S. and Hall, C.E. (2001) Variable-Structure PID Control to Prevent Integrator Windup. IEEE Transactions on Industrial Electronics, 48, 442-451. http://dx.doi.org/10.1109/41.915424
- Matsuda, Y. and Ohse, N. (2006) An Approach to Synthesis of Low Order Dynamic Anti-Windup Compensations for Multivariable PID Control Systems with Input Saturation. Proceedings of the 2006 Joint SICE-ICASE Conference, Busan, 18-21 October 2006, 988-993. http://dx.doi.org/10.1109/SICE.2006.315736
- Shahruz, S.M. and Schwartz, A.L. (1997) Nonlinear PI Compensators That Achieve High Performance. Journal of Dynamic Systems, Measurement and Control, 11, 105-110. http://dx.doi.org/10.1115/1.2801198
- Kelly, R. (1998) Global Positioning of Robotic Manipulators via PD Control plus a Class of Nonlinear Integral Actions. IEEE Transactions on Automatic Control, 43, 934-938. http://dx.doi.org/10.1109/9.701091
- Tarbouriech, S., Pittet, C. and Burgat, C. (2000) Output Tracking Problem for Systems with Input Saturations via Nonlinear Integrating Actions. International Journal of Robust and Nonlinear Control, 10, 489-512. http://dx.doi.org/10.1002/(SICI)1099-1239(200005)10:6<489::AID-RNC489>3.0.CO;2-D
- Hu, B.G. (2006) A Study on Nnonlinear PID Controllers―Proportional Component Approach. Acta Automatica Sinica, 32, 219-227.
- Huang, C.Q., Peng, X.F. and Wang, J.P. (2008) Robust Nonlinear PID Controllers for Anti-Windup Design of Robot Manipulators with an Uncertain Jacobian Matrix. Acta Automatica Sinica, 34, 1113-1121. http://dx.doi.org/10.3724/SP.J.1004.2008.01113
- Liu, B.S. and Tian, B.L. (2009) General Integral Control. Proceedings of the International Conference on Advanced Computer Control, Singapore, 22-24 January 2009, 136-143.
- Liu, B.S. and Tian, B.L. (2012) General Integral Control Design Based on Linear System Theory. Proceedings of the 3rd International Conference on Mechanic Automation and Control Engineering, 5, 3174-3177.
- Liu, B.S. and Tian, B.L. (2012) General Integral Control Design Based on Sliding Mode Technique. Proceedings of the 3rd International Conference on Mechanic Automation and Control Engineering, 5, 3178-3181.
- Liu, B.S., Li, J.H. and Luo, X.Q. (2014) General Integral Control Design via Feedback Linearization. Intelligent Control and Automation, 5, 19-23. http://dx.doi.org/10.4236/ica.2014.51003
- Liu, B.S., Luo, X.Q. and Li, J.H. (2013) General Concave Integral Control. Intelligent Control and Automation, 4, 356-361. http://dx.doi.org/10.4236/ica.2013.44042
- Liu, B.S., Luo, X.Q. and Li, J.H. (2014) General Convex Integral Control. International Journal of Automation and Computing, Accepted.
- Khalil, H.K. (2007) Nonlinear Systems. 3rd Edition, Electronics Industry Publishing, Beijing, 126-128, 482-484.







