Open Journal of Fluid Dynamics
Vol.06 No.03(2016), Article ID:70544,16 pages
10.4236/ojfd.2016.63015
Effect of Cooling Intensity and Position on Solidification in Semi-Continuous Casting of Copper
Amar H. Hameed1*, Ahmed A. Mohammed2, Obaid T. Fadhil2
1Mechanical Engineering Department, KTO Karatay University, Konya, Turkey
2Mechanical Engineering Department, University of Anbar, Ramadi, Iraq

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: February 1, 2016; Accepted: September 10, 2016; Published: September 13, 2016
ABSTRACT
Cooling heat flux effect in both primary and secondary cooling zone has been studied in semi-continuous casting of copper billet. Sufficient cooling is essential to reduce casting defects and to get high productivity, however low rate of solidification is aimed in order to get coarser grain size and softer metal for less losses in extrusion. A three-dimensional numerical model has been developed including solidification behavior of copper through mushy zone. At steady state and constant casting speed, solid shell thickness is monitored during the reduction of cooling rate at mould region to avoid breaking out. Heat flux intensity at mould plays important role not only in the formation of solid shell thickness. But, pool length and mushy zone thickness can be significantly increased by decreasing primary cooling intensity. Increase intensity of secondary cooling zone for two particular cases of primary cooling is tested. First case is tested at mould inlet water temperature of 38˚C, and second case at water temperature of 63˚C. Results showed that the combination of increasing secondary cooling intensity and reduction of primary cooling intensity can increase pool length and mushy zone thickness. Also, it is shown that, secondary cooling intensity can be magnified by up to 1.5 times for cooling water temperature of 63˚C to get pool length close to that of water temperature of 38˚C.
Keywords:
Copper, Semi-Continuous, Casting, Primary Cooling, Secondary Cooling, Metal Casting

1. Introduction
Thousands tons of copper are manufactured every year as rods, tubes, bars, and other diverse section products in casting-extrusion-drawing processes. Copper or brass is casted in semi-continuous casting process as solid billets with a soft structure for extrusion purpose. The quality of the extruded rods and tubs depends on the processing factors of casting, extrusion, and drawing. In addition, energy consumption and waste metal discarded during extrusion process also depends on each of the processing parameters for all production processes. The product quality, microstructure, and reduction of casting defects depend essentially on cooling process during casting process. Adequate cooling is required for casting process to accelerate casting process, however extreme and rapid cooling may increase the strength of the billet and in turn increase the energy of extrusion and also increase the quantity of discards in extrusion process. Heat removal rate and direction affect solidification process and in turn it will affect the microstructure of the product. It is well known that the latest physical properties of the product are function of its microstructure. In casting process, as much as grain size is small, the energy consuming will be greater in the following extrusion process, which is not preferable for the manufacturer.
Most of the literatures have focused on heat transfer in steel and aluminum casting [1] [2] . In addition, they have marginalized the effect of heat transfer on the subsequent process (in billet casting the following process is extrusion) [3] . The study of heat transfer in casting of copper round section thin wire is different from that of heavy billet prepared for extrusion. Some literatures have focused on heat transfer in casting mould [4] and through the gap between the mould and the cast [5] . Some other literatures have been dedicated to study the turbulence induced by metal liquid flow [6] . Some other literatures have studied heat transfer in copper strip rather than billets [7] . Hameed and Abd [8] have studied the effect of developing design of nozzles for sufficient and uniform secondary cooling to enhance the quality of casted copper. In this research we try to decrease heat removal at the mould (primary cooling) and increase it at the secondary cooling stage. Solidification process starts at first point of the interface between melted metal and inner mould wall, and then a solidified shell starts forming there. The solidified shell growths and be thicker during solidification process until the solid parts reaches to the center of the billet. Ordinarily, this shell has fine grains especially near the billet surface due to rapid cooling there [9] . Heat is removed in both radial and vertical direction during solidification process. In vertical direction, heat is conducted due to temperature gradient within the billet. In mould region, cooling in radial direction is more dominant, but it has an undesirable consequence on the forming of grains which results in smaller grains and stronger metal. If the primary cooling is reduced and the secondary cooling is increased, then vertical heat removing will be more predominant. As a sequence, grain will have longer time for cooling and it will form larger size [9] .
2. Methodology
At Shaheed Company-Iraq, copper billets with length of the billet up to (6 m), and with a diameter of (18 cm) are produced. A mould with inner diameter of (18 cm) and
length of 30 cm is used for primary cooling. Casting process of copper liquid at a temperature of 1523˚K was monitored and numerically simulated. Molten copper is poured gradually in to the top opening of the mould. Inside the mould, melted copper cooled by passing water through a gap within mould body. Cooling process at mould zone is very important to form the outer surface of the billet and to build the solid shell. Water enters mould cooling water gap from the bottom end and exits from the upper end of the mould gap with flow rate approximately 2.5 m3/h. If cooling process in the mould is inadequate to form strong solid shell to carry the billet, the product fail and the melted metal will flow out. The formed billet is withdrawn from the downside of mould by a hydraulic piston-cylinder system. The system of pulling depends on the amount of poured molten metal. When the casted billet comes out from the lower side of the mould, water is spread on the billet surface by a slot or set of nozzles surrounding the billet. After approximately three meters, billet immerses in a water basin to complete the cooling process. From direct observation of the casting process in the factory, there are many difficulties to use measuring devices to get the data from the real system. Most technicians are relying on direct observation and their experience to complete the process. As a result, numerical simulation is the most suitable method to predict casting process parameters.
Numerical simulation for extracting heat from casting billet in semi-continuous casting process presents in this study. In addition, the primary and secondary cooling effect on the solidification process and mushy zone during semi continuous casting process for copper billet will be studied. For this purpose, a general-purpose CFD package is used. The length of computational domain within the billet considered in this model is (2.3) m. The length of the mould (primary cooling) is (30 cm). While, the length of part downstream the mould, which exposed to the secondary cooling is (2 m).
2.1. Building Grid
Before starting with fluent program, the 3D geometry of the model has been generated and the mesh (grid) has been built using GAMBIT software. The mesh of the billet is explained in the following;
At the top view, the liquid entrance area or pouring zone is the small quadrilateral mish area in Figure 1, while the area around the entrance area is considered as a top zone of the billet which loses heat by radiation to the ambient. Surface of the billet which exit from mould is called the secondary cooling zone which has a length of two meter. This zone is subdivided into six different thermal boundary conditions regions for the purpose simulating different cooling intensity regions. The first region has a length of 10 cm to avoid touching of water spray to the mould. It is characterized by heat radiation only. Remain five parts have a length of 30 cm for each of them, except the final part which has a length of 40 cm. In addition, all the boundaries of this model are subjected to heat loss except the entry and exit.
In FLUENT software, enthalpy-porosity formulation is used to solve solidification and/or melting taking place at one temperature (e.g., in pure metals) or over a range of temperatures (e.g., in binary alloys). The liquid-solid mushy zone treated as a porous
Figure 1. Mesh of top view of computational domain at the inlet of billet (top view).
zone with porosity equal to the liquid fraction. In enthalpy-porosity technique, the melt-solid interface do not tracked explicitly. Instead, a quantity called the liquid fraction, which indicates the fraction of the cell volume that is in liquid form, is associated with each cell in the domain. For each single iteration, the liquid fraction is computed based on an enthalpy balance. Mushy zone is a region in which the liquid fraction lies between (0 and 1.0). Mushy zone is modeled as a “pseudo” porous medium in which the porosity decreases from 1 to 0 as the material solidifies. When the material has fully solidified in a cell, the porosity becomes zero and hence the velocities drop to zero.
2.2. Governing Equations
2.2.1. Energy Equation
For solidification region, the energy equation can write equally
 (1)
(1)
where; H is enthalpy,  is density,
is density,  is fluid velocity, and S is source term. The enthalpy of the material is computed as the sum of the sensible enthalpy, h, and the latent heat of the components ∆H [10] ,
is fluid velocity, and S is source term. The enthalpy of the material is computed as the sum of the sensible enthalpy, h, and the latent heat of the components ∆H [10] ,
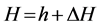 (2)
(2)
where:
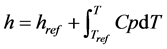 (3)
(3)
where; href is reference enthalpy, Tref is reference temperature, and Cp is specific heat at constant pressure. Liquid fraction β can be defined as;
β = 0 if T < TSlidous
β = 1 if T > Tliquidus
 for TSlidous < T < Tliquidus (4)
for TSlidous < T < Tliquidus (4)
Equation (4) refers to the lever rule. The latent heat content can vary between zero (for a solid) and L (for a liquid). The latent heat of melting content can be written in terms of the latent heat of the material in a liquid form L as follows;
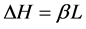 (5)
(5)
The solution for temperature results from iteration between the energy Equation (1) and the liquid fraction Equation (4). Directly using Equation (4) to update the liquid fraction usually results in poor convergence of the energy equation. In FLUENT, the method suggested by Voller and Swaminathan is used to update the liquid fraction. For pure metals, where TSlidous and Tliquidus are equal, a method based on specific heat, given by Voller and Prakash is used instead.
2.2.2. Momentum Equations
The enthalpy-porosity technique treats the mushy region (partially solidified region) as a porous medium. The porosity in each cell is set equal to the liquid fraction in that cell. In fully solidified regions, the porosity is equal to zero, which extinguishes the velocities in these regions. The momentum sink due to the reduced porosity in the mushy zone takes the following form [10] ;
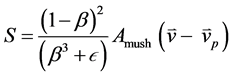 (6)
(6)
where β is the liquid volume fraction,  is a small number (0.001) to prevent division by zero, Amush is the mushy zone constant equal 105 for almost cases, and
is a small number (0.001) to prevent division by zero, Amush is the mushy zone constant equal 105 for almost cases, and  is the solid velocity due to the pulling of solidified material out of the domain (called pull velocity ). The mushy zone constant measures the amplitude of the damping; the higher this value, the steepest the transition of the velocity of the material to zero as it solidifies. Very large values may cause the solution to oscillate. The pull velocity is included to account for the movement of the solidified material as it is continuously withdrawn from the domain in continuous casting processes. The presence of this term in equation (6) allows newly solidified material to move at the pull velocity. In continuous casting processes, the solidified matter is usually continuously pulled out from the computational domain. Therefore, the solid stuff will cause a finite velocity that needs to account for in the enthalpy-porosity technique.
is the solid velocity due to the pulling of solidified material out of the domain (called pull velocity ). The mushy zone constant measures the amplitude of the damping; the higher this value, the steepest the transition of the velocity of the material to zero as it solidifies. Very large values may cause the solution to oscillate. The pull velocity is included to account for the movement of the solidified material as it is continuously withdrawn from the domain in continuous casting processes. The presence of this term in equation (6) allows newly solidified material to move at the pull velocity. In continuous casting processes, the solidified matter is usually continuously pulled out from the computational domain. Therefore, the solid stuff will cause a finite velocity that needs to account for in the enthalpy-porosity technique.
2.3. Numerical Model Setting
Steady state: semi-continuous casting differs from other solidification processes by its steady state nature, relative to an outside observer in a laboratory frame of reference [11] . Solidification and melting choice allows setting parameters related to the solidification/melting model. In addition, this option includes a pull-velocities option, where the FLUENT will account for the cause of the solidified material as it continuously drawn from the field in the continuous casting operation.
Thermal conductivity of copper is temperature dependent and its value changes according to the material composition and thermal history. Hence, the application of wide temperature ranges of thermal conductivity is necessary for a realistic simulation of heat transfer analysis in a semi continuous casting operation. The specific heat, which is defined per unit mass (J/kg∙k), is required for the Enthalpy formulation. The latent heat treated using an apparent enthalpy/specific heat method where the heat generation term eliminated. The specific heat CP is required for the solution of the integral equation in enthalpy method for the same temperature range as has been defined in the thermal conductivity-temperature relationship. For copper with temperature range between Tl − Ts (mushy zone) the material starts to convert from liquid to solid. During this conversion, the latent heat of fusion and the sensible heat (specific heat time’s temperature) released simultaneously. It is necessary to treat the sensible heat and the latent heat of solidification simultaneously. Density of copper in continuous casting varies from liquid to solid with temperature between 8000 - 8900 kg/m3. Table 1 [12] shows properties of copper as a function of temperature.
Some properties of copper assumed constant at different temperature as has been mentioned in several literatures [7] [13] . Table 2 shows properties of copper, which constant at any temperature.
Boundary Conditions
At Shaheed Company during semi continuous casting process, the temperature of melting copper at the inlet is 1523 k. Similarly there are many research take this temperature [14] [15] . The velocity of fluid is 0.0209766 (m/s) which is calculated from the continuity equation for a specified pull velocity. When the liquid copper solidifies, it must firstly waste its superheating energy and then the (solidification/fusion) latent heat. Superheat is the heat which results from the difference in temperature between the liquidus temperature of the copper and the temperature of the copper liquid when it enters the mould. Typically, the superheat is about (20˚C - 40˚C) [9] .
Table 1. Properties of copper depending on temperature.
Table 2. Properties of copper which temperature independent.
Heat transfer from the billet to the mould is really complex and include a range of different heat transfer operations, thus it is difficult to examine each occasion separately [16] . Heat flux removal from the mould is controlled by convection equation. This equation is written for the trend of heat flux calculated from mould wall temperature, water temperature, and heat transfer coefficient predicted in the literature [5] . In this study, heat flux is decreased by increasing inlet water temperature to the mould for fixed water mass flow rate. Heat flux is reduced until shill thickness be very thin to withstand breaking out in order to avoid process failure by metal defuse out of the billet. The difference between the inlet and outlet water normally about (4˚C - 6˚C) as has been stated in the literature [17] .
Initially, heat flux is calculated for inlet water temperature Tw = 23˚C and outlet Tw = 29˚C, and listed against the vertical distance as shown in Table 3. In this table, heat flux is calculated locally for each heat transfer coefficient, mould wall temperature, and local water temperature. The cooling water inters to the mould from mould downside and the temperature increases linearly until it reaches the maximum at the top of the mould. The height of the mould is subdivided into equal spaces while wall temperature is assumed to have linear distribution throughout the mould height. The heat flux is drawn against the vertical height as shown in Figure 2. By using the graph, the trend equation is formed for heat flux behavior throughout the mould height to be used as variable heat flux for the boundary condition of the numerical solution. The trend equation is used as a heat flux and included in user-defined function (UDF) for the boundary condition of simulation. We set the wall of mould as a moving wall and its speed 0.002 (m/s) to simulate the movement of the billet regarding to the mould.
We increase inlet water temperature to exam the effect of reducing heat flux on pool length, solid shell thickness and mushy zone thickness. The next step, the inlet water temperature has been change from Tw = 23˚C to Tw = 38˚C by a step of five degrees and so on for the next step. After Tw = 43˚C, inlet water temperature increases by 10 degree because the impact of increased temperature was not significant. At the exit of the mould, we draw an imaginary horizontal line in the numerical model to test the thickness of solid shell and mushy zone using liquid fraction. Along the billet centerline, we also draw an imaginary line in the numerical field to test pool length and mushy zone thickness at the tip of solidification.
Table 3. Heat flux versus mould height for Tw = 23˚C.
Figure 2. Heat flux versus mould height for Tw = 23˚C.
Secondary cooling zone divided to seven zones to deal with distribution of heat transfer coefficient along wall of secondary cooling. Total length of secondary cooling zone is 2 m. Length of each sub zone of secondary cooling is 30 cm except sub-zones one and last, they are (10 cm) and (40 cm) respectively. We set all secondary cooling zones as a moving wall and its speed 0.002 (m/s) to simulate the movement of billet surface regarding to the water spray of secondary cooling.
Heat transfer coefficient on first zone after billet exit from mould very little, because this zone does not exposed to spray water directly. In second zone, the spray water nozzle affect concentrated, thus heat transfer coefficient is the largest. Heat transfer coefficient decreases gradually in the rest of the other zones, as a result moving away from the source of cooling and a thin layer of vapor is formed on the wall of billet. Heat flux removal at secondary cooling region is controlled by convention equation (Newton’s law of cooling). This equation can be obtained from heat transfer coefficient and the difference between water spray temperature and wall strand temperature. Heat transfer coefficient predicted in the literature [18] . The values of heat transfer coefficient in modified by increasing them linearly, whereas the values of heat transfer coefficient jump steeply from one zone to other. Table 4 shows the values of heat transfer coefficient for different cases. Case (a) represent heat transfer coefficient as in the literature. Other cases were obtained from the magnification of case (a) as a result of multiplication by 2, 3, 4, 5, 6 and 7 respectively, to simulate the increase in cooling intensity.
3. Results and Discussions
In this section, the results of controlling heat removal process from the casted billet in both primary cooling and secondary cooling regions are shown.
Table 4. Heat transfer coefficient (W/m2) distribution during different cases.
3.1. Primary Cooling
Liquid fraction along the billet centerline is considered in the numerical results to calculate the depth of the liquid pool and mushy zone thickness at solidification tip, where liquid fraction equals 0 for the solid, 1 for the liquid, and lay between 0 and 1 for mushy zone metal. Liquid fraction throughout a section at the mould exit is also considered to predict the thickness of solid shell at mould exit section and mushy zone thickness at the same section.
During solidification process, the length of the pool is affected by cooling in both primary and secondary cooling regions. This length will provide an evidence of cooling rate and direction. Logically, longer pool length refers to longer time of solidification for constant speed casting, and same thing can be said for thicker mushy zone. Mushy zone is solidified late below the exit section, this promise to form the desirable grain size which depends on cooling rate in secondary cooling. Whenever, solid shell region solidifies completely within mould region due to high temperature difference in the mould region which results in higher cooling rate. As a result, grain size will be small in solid shell region.
In Figure 3, heat fluxes are drawn for varying inlet water temperatures. Cooling rates are the higher at the top of the mould (y = 0.3 m), and heat exchange decreases with decreasing temperature difference between the metal and cooling water. High cooling rate at the topside of the mould results in forming hard shell with fine grain size. Cooling water inlet temperature is stepped by 5˚C for the first four cases to get reasonable change in heat flux. The step is doubled after that because the changes in shell thickness are trivial, and heat flux amount decreases with rising cooling water temperature. Where pool length and mushy zone thickness at solidification tip are very sensitive for any change in heat extracting in mould region as has been stated in previous studies [19] , and in the results below. The changes in heat flux are more significant at the upper half of the mould where the metal is partially liquid and the convective heat is more sensitive to cooling water temperature.
Approximately, pool length increases linearly with increasing cooling water inlet temperature as appears in Figure 4. However, there are some fluctuations in the trend line, but these fluctuations may belong to some numerical issues rather than physical effects.
Figure 3. Heat flux in mould region for different inlet water temperature.
Figure 4. Varying pool length with increasing inlet water temperature.
These decreasing of extraction heat flux from mould allow some superheating energy and latent heat in the molten metal to stay out of mould region. Thus pool length becomes longer and mushy zone thickness at tip increasing linearly and slightly until reach to (0.25 m) as appears in Figure 5. However, the changes in mushy zone thickness look comparatively little (one centimeter for each step of decreasing of heat flux), but these changes are significant indicator for the cooling rate in solidification process. Any little change in mushy zone thickness will give the grains of metal longer time to grow and build larger grain boundaries. The advantage of increasing pool length is to allow more amount of heat transfer in the vertical direction instead of wasting heat rapidly in radial direction. It also contributes to provide long time for solidification
Figure 5. Varying mushy zone thickness against inlet water temperature.
process and allow the grains to grow in all directions to form more likely equiaxed grain shape. This long time assisted to form coarse grain size for billet of copper. These increasing’s in length of molten metal pool and thickness of mushy at tip are desired in general, but it may cause some defect in the surface of product. These defect appear if pool length increased out of limited range, which explained in several previous literatures [20] .
At the mould exit section, the solid shell thickness doesn’t change with the variation of the mould inlet water temperature from 23˚C to 38˚C. It is about fixed value of 0.0125 m, as shown in Figure 6. However, it suddenly decreases to 0.0045 m for lower heat flux at inlet water temperature of 43˚C. Then the solid shell thickness fixed at 0.0045 m until water temperature reaches to 73˚C. Continuous decreasing in heat flux causes further solid shell thickness decreasing. Further decreasing in the shell thickness may cause breakout failure, because of the static head pressure supplied by liquid metal in the mould [5] [21] . When cooling water temperature is lower than 38˚C, heat flux in the mould is enough to produce a thick shell. Above than 38˚C, the shell thickness jumps directly to a small value due to smaller temperature differences between water and mould wall. This may refer to the role of local temperature difference between water and mould wall for the same selected heat transfer coefficient and its impact on convection process. Mushy zone thickness at mould exit section is approximately not affected significantly by the reduction of the primary cooling heat flux. However, both shell thickness and mushy zone thickness degrade clearly at (73˚C), which means that decreasing heat flux to this point definitely is not suitable for this process.
3.2. Secondary Cooling
In the first section, Heat flux extraction from mould wall is reduced by increasing water inlet temperature. The focus was on the effect of these changes on the pool length, the
Figure 6. Solid shell thickness and Mushy zone at exit section for a range of inlet water temperature Tw.
solid shell thickness and mushy zone thickness at solidification tip and exit section of the mould.
In this study, two cases of primary heat flux are selected for examining the secondary cooling zone relatively to a specified primary cooling quantity. One of these cases is selected at the mould inlet water temperature (Tw = 38˚C) (moderate primary cooling). The other case is selected at the mould inlet water temperature (Tw = 63˚C) (low primary cooling). In both cases, solid shell thickness should be enough for keeping molten metal to prevent it from diffuse to outer area. The first selected case (at Tw = 38˚C) represents point after it solid shell thickness reduced to the less acceptable thickness. Solid shell thickness and mushy zone thickness at exit mould is the same with the higher cooling rates at the mould, however it has longer pool length. The second selected case (at Tw = 63˚C) represents point at which pool length is longer than other cases as well as it represent a critical point for shell thickness. Also solid shell thickness is the same for cases that preceded it after the first selected case. After this case (at Tw = 73˚C) molten metal may be break the shell out and diffuse to the circumference of the billet.
In Figure 7, we notice the length of pool molten metal inversely proportional to the increase of heat flux extracted from the secondary cooling zone. As well as, the thickness of mushy zone at tip of solidification decreases with increasing heat flux extraction from secondary cooling zone as shown in Figure 8. However, there are significant differences between the cases of the temperature 38˚C and the second selected case of the temperature 63˚C. It is noted that the first case move into the solid phase faster than in the second case. This is because the heat that has been removed in the first case higher than in the second during the primary cooling. For low cooling fluxes (a) and (b), extraction heat flux from secondary cooling is not sufficient to dissipate all latent heat and superheating energy, thus pool length extends beyond the numerical field (>2.3 m) of the billet in both selected cases.
Figure 7. Pool length versus different heat flux intensity.
Figure 8. Mushy zone thickness at solidification tip for different secondary cooling intensity cases.
In Figure 7 and Figure 8, both pool length and mushy zone thickness are distinguished and within the computational field of this study in the cases c, d, e, f, and g. Also, solid region, molten region and mushy zone region are clear and distinct. Also show that the first case for each cooling intensity stage has shorter pool length and less mushy zone thickness compared with that of the second case for same subjected secondary cooling. However, we can notice in the figures approximately we need to increase secondary cooling by 1.5 times in second case to achieve same pool length and same mushy zone thickness of the first case. Sufficient cooling in secondary cooling is preferred to accelerate the process, but longer pool length is also important to get coarser grain size. That mean increasing the intensity of cooling in secondary cooling is achievable with enough pool length for lower cooling in primary zone. The drop in the length of pool as a result of increased heat flux extracted from the secondary cooling zone for both cases is clear in Figure 7. Pool length approaches to be constant for high cooling rates, which promises high readiness of increasing intensity of secondary cooling. Recalling that, heat flux in case (g) is 1.75 times of that in case (d). However, pool length increases by only 15 cm from case (d) to case (g) in first case and by 27 cm in the second case. In other hand, heat flux in case (d) is two times of that in case (b), but pool length difference is 40 cm in first case and more than 70 cm in the second case. In addition, the difference between the two cases is high only in the lower secondary cooling effect (cases a, b, c, and d). However, this difference decreases when secondary cooling plays greater role (cases e, f, and g). Figure 8 shows the drop in mushy zone thickness at the tip of solidification for all cases. However, mushy thickness decreases with cooling rate for both cases, but the difference between them still high with little decreasing due to the effect of primary cooling.
4. Conclusion
Primary cooling intensity reduction is applicable to increase pool length and mushy zone thickness, but it is restricted to a specific limit to avoid failure of casting process. Since, reduced primary cooling will reduce the productivity and results in a lot of casting defects like bending of the billet and high rate of surface oxidization, higher rate secondary cooling is required. Results show the applicability of higher secondary cooling intensity for reduced primary cooling. However, higher secondary cooling reduces pool length and mushy zone thickness. But by its combination with reduction of primary cooling, intensity of secondary cooling can be severely amplified. For 25˚C temperature difference between first and second case of water inlet temperature for primary cooling, secondary cooling can be magnified by (1.16 the ratio g/f) to (1.5 the ratio of c/b) in low primary cooling case (63˚C) to get pool length and mushy zone thickness not less than that of high primary cooling case (38˚C).
Conflict of Interest
Shaheed Company of copper and brass in Iraq is interested in this research and it has supported the research by technical information without any financial support.
Cite this paper
Hameed, A.H., Mohammed, A.A. and Fadhil, O.T. (2016) Effect of Cooling Intensity and Position on Solidification in Semi-Continuous Casting of Copper. Open Journal of Fluid Dynamics, 6, 182-197. http://dx.doi.org/10.4236/ojfd.2016.63015
References
- 1. Louhenkilpi, S., et al. (2005) 3D Steady State and Transient Simulation Tools for Heat Transfer and Solidification in Continuous Casting. Materials Science and Engineering: A, 413, 135-138.
http://dx.doi.org/10.1016/j.msea.2005.08.153 - 2. Kim, M.-S. and Kumai, S. (2013) Solidification Structure and Casting Defects in High- Speed Twin-Roll Cast Al-2 mass% Si Alloy Strip. Materials Transactions, 54, 1930-1937.
http://dx.doi.org/10.2320/matertrans.L-M2013824 - 3. Xu, X., Zhang, W. and Lee, P. (2002) Tree-Ring Formation during Vacuum Arc Remelting of INCONEL 718: Part II. Mathematical Modeling. Metallurgical and Materials Transactions A, 33, 1805-1815.
http://dx.doi.org/10.1007/s11661-002-0189-z - 4. Cho, K.-H. and Kim, B.-M. (2008) Numerical Analysis of Secondary Cooling in Continuous Slab Casting. Journal of Materials Science and Technology, 24, 389-390.
- 5. Janik, M. and Dyja, H. (2004) Modelling of Three-Dimensional Temperature Field inside the Mould during Continuous Casting of Steel. Journal of Materials Processing Technology, 157, 177-182.
http://dx.doi.org/10.1016/j.jmatprotec.2004.09.026 - 6. Mahapatra, R., et al. (1991) Mold behavior and Its Influence on Quality in the Continuous Casting of Steel Slabs: Part I. Industrial Trials, Mold Temperature Measurements, and Mathematical Modeling. Metallurgical Transactions B, 22, 861-874.
http://dx.doi.org/10.1007/BF02651163 - 7. Blase, T., et al. (2004) A 3D Conjugate Heat Transfer Model for Continuous Wire Casting. Materials Science and Engineering: A, 365, 318-324.
http://dx.doi.org/10.1016/j.msea.2003.09.042 - 8. Tsai, D. and Hwang, W. (2012) Numerical Simulation of the Solidification Processes of Copper during Vacuum Continuous Casting. Journal of Crystal Growth, 343, 45-54.
http://dx.doi.org/10.1016/j.jcrysgro.2011.12.074 - 9. Vynnycky, M. (2013) On the Role of Radiative Heat Transfer in Air Gaps in Vertical Continuous Casting. Applied Mathematical Modelling, 37, 2178-2188.
http://dx.doi.org/10.1016/j.apm.2012.05.005 - 10. Sahin, H.M., et al. (2006) Determination of Unidirectional Heat Transfer Coefficient during Unsteady-State Solidification at Metal Casting-Chill Interface. Energy Conversion and Management, 47, 19-34.
http://dx.doi.org/10.1016/j.enconman.2005.03.021 - 11. Thomas, B.G. (2002) Modeling of the Continuous Casting of Steel—Past, Present, and Future. Metallurgical and Materials Transactions B, 33, 795-812.
- 12. Fluent, I. (2006) Fluent 6.3 Users Guide. Fluent Documentation. ©Fluent Inc.
- 13. Bauser, M. and Siegert, K. (2006) Extrusion. ASM International, Ohio.
- 14. Hameed, A. and Abed. A. (2014) Effect of Secondary Cooling Configuration on Microstructure of Cast in Semi-Continuous Casting of Copper and Brass. Applied Mechanics and Materials, 575, 8-12.
http://dx.doi.org/10.4028/www.scientific.net/AMM.575.8 - 15. Mahmoudi, J., et al. (2003) An Experimental and Numerical Study on the Modelling of Fluid Flow, Heat Transfer and Solidification in a Copper Continuous Strip Casting Process. Materials Transactions, 44, 1741-1751.
http://dx.doi.org/10.2320/matertrans.44.1741 - 16. Ruhul Amin, M. and Mahajan, A. (2006) Modeling of Turbulent Heat Transfer during the Solidification Process of Continuous Castings. Journal of Materials Processing Technology, 174, 155-166.
http://dx.doi.org/10.1016/j.jmatprotec.2005.11.035 - 17. Kelly, J., et al. (1988) Initial Development of Thermal and Stress Fields in Continuously Cast Steel Billets. Metallurgical Transactions A, 19, 2589-2602.
http://dx.doi.org/10.1007/BF02645486 - 18. Vapalahti, S., Louhenkilpi, S. and Raisanen. T. (2006) The Effect of Fluid Flow on Heat Transfer and Shell Growth in Continuous Casting of Copper. Materials Science Forum, 508, 503-508.
- 19. Shi, Z. and Guo, Z. (2004) Numerical Heat Transfer Modelling for Wire Casting. Materials Science and Engineering: A, 365, 311-317.
http://dx.doi.org/10.1016/j.msea.2003.09.041 - 20. Hardin, R.A., et al., (2003) A Transient Simulation and Dynamic Spray Cooling Control Model for Continuous Steel Casting. Metallurgical and Materials Transactions B, 34, 297-306.
http://dx.doi.org/10.1007/s11663-003-0075-0 - 21. Lait, J., Brimacombe, J. and Weinberg, F. (1974) Mathematical Modelling of Heat Flow in the Continuous Casting of Steel. Ironmaking Steelmaking, 1, 90-97.










