Received 1 February 2015; accepted 22 February 2015; published 28 February 2015

ABSTRACT

Alcohol influences human health condition by starving red blood cells (RBCs) of oxygen, which results in poor blood circulation. Starved RBCs clump together and restrict blood flow, especially in capillaries. In this study, a finite element method-based moving mesh technique was applied to simulate the motion and deformation of a single RBC under different flow conditions. A 2-D model of a single RBC floating in plasma-alcohol solution was created using Arbitrary Lagrangian-Eule- rian (ALE) method with moving mesh for a fluid structure interaction problem. Cell deformability and stability were studied in an alcoholic plasma solution at different fluid flow conditions. Poor blood circulation was observed with RBC tending to rotate and oscillate at low flow rates. Moreover, RBC exhibited a parachute shape while moving without oscillation, which indicated improved micro-circulation at increased flow rates. In both cases, RBC exhibited a parachute shape while moving through micro-channel at increased flow rates. The simulation also showed the significant increase of RBC deformability with the increasing viscosity of plasma as a result of alcohol presence in blood.

Keywords:

Moving Mesh, Fluid Structure Interaction, Alcohol, RBC, Microvessel, Deformability, Micro-Circulation

1. Introduction

A healthy and long life is a prime concern for every human being. Among the major threats to a long lifespan are circulatory diseases, which are related to the circulation of blood and its components (i.e., blood cells and plasma) in the body. Hematocrit in human arteries is about 40%, and this value is even lower in micro-vessels, such as capillaries. An abnormality in the morphology of healthy red blood cells (RBCs) and blood flow velocity may lead to a circulatory disease, which may increase in severity at the micro-scale. Many experimental and numerical studies have been conducted to improve the current knowledge and understanding of the interaction between RBCs and plasma in micro-vessels [1] -[3] .

Under normal conditions, RBCs are biconcave-shaped discs of about 8 μm in diameter. The membrane of the cell is highly deformable to external forces and returns to its original shape after the removal of forces [4] . Blood flow rheology in micro vessels is affected considerably by RBC deformability, which may be determined by the mechanical properties of the membrane and its internal fluid. In general, the degree of RBC deformability is controlled by the flexibility of the cell membrane. Therefore, numerous measurements and simulations of cell membrane rheology have been performed on populations of RBCs and at the single-cell level [5] [6] .

Alcohol is a factor that influences human health condition; its presence in the body starves RBCs of oxygen, thickens the blood, and kills cells, resulting in poor blood circulation [7] [8] . Starved RBCs clump together and restrict the blood flow in small blood vessels and capillaries. Over time, alcohol intake reduces the production of RBCs, which are essential in maintaining oxygen supply to the skin, muscles, liver, and pancreas. Previous studies have focused on the influence of alcohol on blood flow, RBCs, and plasma [9] [10] . Experimental studies that have been conducted have focused on the effects of the mechanical properties of RBCs under alcoholic influence; however, these earlier works restricted their analysis only to RBC deformability under different alcoholic concentrations without tracking RBCs in a micro-vessel [11] . Although numerical simulation tools are fully capable of tracking RBC motion and deformation in a micro-vessel, no numerical study has ever considered the alcoholic influence on RBC motion and deformation in a microcapillary using the fluid structure interaction (FSI). Therefore, the current work aims to fill the research gap on the mechanics of RBCs under alcoholic influence in a microcapillary using FSI technique to investigate motion and deformation.

In this study, a finite element method-based moving mesh technique was applied to simulate the motion and deformation of a single RBC under different flow conditions. The effects of blood plasma viscosity and velocity due to alcohol consumption on RBC behavior and deformability while moving through a microcapillary channel were investigated. This study could provide theoretical knowledge on RBC behavior at the micro-scale level.

2. Mathematical Modeling and Governing Equations

A 2-D simulation model was created for RBC motion in plasma fluid between two parallel plates. The length of flow channel L and the distance between the plates D are 100 and 10 μm, respectively. RBC was placed 15 μm from the inlet of the channel, as shown in Figure 1.

Governing Equations

The interaction of an incompressible fluid and rigid structure belongs to the class of fluid-structure interaction problems. The equation for the motion of an incompressible Newtonian liquid is described by the Navier-Stokes equations:

(1)

(2)

where 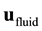is fluid velocity, 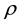is fluid density, is identity tensor, 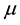is viscosity, is pressure, and 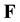is body force or volumetric force.

The behavior of the cell and membrane interaction with fluid is described by the following elastodynamic equation:

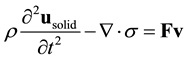(3)

where is the Cauchy stress tensor, and 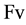represents the force per unit volume.

The hyperelastic smoothing method was used to simulate the mesh deformation:

(4)

where 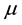and 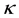are artificial shear and bulk moduli, respectively, and the invariants and are given by

(5)

The fluid and solid sub-domains of the cell can be coupled via one-way or two-way method. Coupling is one- way if the changes in one physics affect the other and in return the second physics does not influence the first one. However, if the influenced physics also affects the first one, then this is called a two-way coupling. The problem becomes more complicated if cell motion is induced by fluid flow, and at the same time, the fluid flow pattern is influenced by cell motion. Variation in the pressure and viscous forces on the particle surface leads to a rise in the forces acting on RBC and can be computed in two ways:

1) Integration of fluid stresses along the RBC contour, i.e., integration of forces acting on the vicinity of the cell.

2) Integration of all the forces and stresses along the boundaries of the computational domain, i.e., forces on the body in terms of the momentum flux far from the body, which does not require knowledge of the flow in the vicinity of the body.

A constant and uniform velocity at the inlet was applied to the RBC. At the outlet, zero pressure was applied, and a no-slip wall condition was set up along the inner walls.

3. Material Properties

The cell was assumed to have hyperelastic properties, which is defined as a material that can completely recover its original shape. The model used in the present work involves an elastic cell with a membrane structure filled with cytoplasm having plasma density and viscosity equal to 6e−3 Pa-s. The literature values for Young’s modulus of RBC vary from 26 kPa to 54 kPa; the value of 30 kPa was chosen for use in this study as an average value [12] . The value of Poisson’s ratio used during the simulation was 0.49.

The blood vessel was assumed to be rigid, and plasma was assumed as homogeneous. Incompressible Newtonian fluid was set to have viscosity of µ = 1.2e−3 Pa-s and density of ρ = 1057 kg/m³ (assuming the presence of alcohol at 1 ml/kg). The Arbitrary Lagrange-Euler (ALE) mesh was used to simulate the moving part of the fluid due to large deformation of the cell. The cytoplasm was considered to have the same density as plasma, and with viscosity of µ = 6e−3 Pa-s [13] .

4. Numerical Implementation

In solving the stated problem, a commercial code for finite element analysis known as COMSOL Multiphysics (V 4.2a) was utilized. A 2-D model with dynamic meshes was created, and a fully coupled solver was used by coupling a solid and a fluid domain together via a direct two-way coupling formulation. Thus, fluid forces deformed the solid domain, and in turn, deformed solid affected the fluid domain. Figure 1 shows the model used for simulating the motion and deformation of a single RBC.

First, a transient analysis of a single RBC in the microcapillary vessel filled with fluid was carried out by using direct computation. The movement of the cell was restricted only to a small displacement before the mesh deformed. Many inverted coordinates were present, and mesh quality became too low to ensure accurate computation. A prescribed mesh displacement methodology was used to overcome this problem. For this purpose, the cell was placed into a rectangular frame that was given a displacement, and at the same time, fluid structure interaction between the RBC and fluid was calculated inside the rectangular frame. In this case, the mesh was not skewed, and an acceptable quality remained until the end of the simulation. The forces acting on the cell were obtained by integrating the entire surface. Deformation plots were obtained using the post-processing tools. Figure 2 shows the schematic of the model with triangular meshes. Figure 2(a) illustrates the initial condition of a cell in the mesh, and Figure 2(b) represents the deformed moving cell and mesh.

5. Results and Discussion

The 2-D model of a single moving RBC through a microvessel under normal and abnormal velocities and viscosities induced by alcohol was created using ALE method for finite element analysis. Simulations with different velocity and viscosity magnitudes were performed to distinguish varied RBC behaviors during its motion through the microcapillary.

The simulation results showed that microcirculation can be improved by increasing flow velocity. With velocity of v = 0.001 m/s, RBC moved along the length of the channel with a deformed bio-concave so-called parachute shape, as shown in Figure 3(a). With a velocity of v = 0.0001 m/s, RBC started rotating with a partially deformed bio-concave shape, and after the longitudinal axis of the RBC nearly paralleled the flow direction, it began oscillating about this position, as shown in Figure 3(b). Reduced blood flow velocity results in poor microcirculation, which leads to oxygen and nutrient deficiency in tissues and organs.

In implementing the effects of alcohol-induced reduced viscosity on the behavior of RBC, the viscosity of plasma was set to 5e−3 Pa-s, and for cytoplasm, it was 6e−3 Pa-s. For the same value of velocity and with different viscosities of plasma and cytoplasm, the deformability of RBCs increases [14] . Figure 4 illustrates that by changing the cytoplasm-to-plasma viscosity ratio, RBC behavior changes. Figure 4(a) shows the total displacement of the moving cell, as well as the extent of cell deformation while moving through the vessel in case of velocity of 0.001 or 0.0001 m/s, respectively. The figures confirm the increased deformation of RBC compared with that in Figure 3(a). Figure 4(b) also presents increased cell deformation, and RBC shows more stable motion through the capillary. However, a rare part of RBC in Figure 4(a) and Figure 4(b) are smaller compared with those in Figure 3(a) and Figure 3(b).

Figure 5 and Figure 6 represent the shear rate plot at different time steps depending on the inlet velocity and viscosity of the plasma flowing through the microcapillary. For the same flow conditions, an increase in viscosity of the plasma solution decreased the shear rate by half, becoming constant after 0.03 s. On the other hand, an increase in velocity increased the shear rate up to 0.03 s for the same viscosity. These two results verify the relation between velocity and viscosity.

Figure 7 illustrates the variation of the ratio of transverse diameter over axial diameter with respect to time for different cytoplasm viscosity and plasma velocity values. Alcohol influences blood velocity. The physiological and pharmacological actions of ethanol are influenced by molecules penetrating into the membrane, which leads to changes in shape, function, and interactions of the membrane proteins [15] . The proposed model could shed light on the issue of how the different factors influence RBC behavior in a microvessel. In this approach, the RBC was represented by a 2-D viscoelastic element filled with liquid, namely, cytoplasm. The 2-D model allowed significant reduction of the calculation time and simplification of modeling. In the present model, the

moving mesh technique with physics-controlled mesh was utilized to calculate the mechanical behavior of the single RBC moving through a microcapillary. The model aided the investigation on the relationship among cell deformability and various other parameters, such as plasma viscosity, blood flow velocity, and material properties.

The model successfully represented the phenomenon of fluid structure interaction of RBC floating in plasma through a microcapillary vessel. It can be useful for simulation of fully coupled problems, such as fluid and cell interaction, as it takes into account many parameters during calculation, which is helpful in understanding the blood flow mechanism from a micro-scale point of view. Although the model is simplified, compared with developed approaches and methods, it can be extended and applied in simulating more complex and realistic problems.

6. Conclusions

A 2-D model has been developed to predict shapes and behavior of a single RBC moving in a microcapillary filled with plasma alcohol solution under different velocities and elasticity parameters. This simulation provides access to a large panel of data for better understanding of the RBC, particularly involving alcohol-influenced behavior at the micro level. Moreover, it helps to explain the consequences of pathologies related to alcohol consumption. Damaged RBCs do not clot properly because the blood becomes too thin. In terms of diameter, microvessels are about one billion times larger than RBC, which make them very important for blood circulation. As such, the rheological properties and behavior of a single RBC have great influence on blood flow. Therefore, problems related to RBC behavior, such as decreased flow velocity in the microcapillary, increased viscosity, and others, will lead to severe conditions for the entire human body.

The numerical simulations are made by utilizing a time-dependent coupling: ALE equations, Navier-Stokes equations, and structural mechanics model of RBCs with non-zero thickness membrane. The obtained results for plasma flow and biconcave RBC motion reveal that the proposed model successfully simulates RBC deformation during capillary flow, and shows RBC dependence on plasma velocity and viscosity. The deformed, so- called parachute shape of RBC has been observed in experiments. Further work on this problem will allow investigating and establishing the behavior of RBC that moves through a stenotic structure in alcohol plasma solution.

Acknowledgements

This work was supported by the Korea Research Foundation (NRF) of Korea, a grant funded by the Korean Government (MEST) (No. 2012R1A2A2A01046099), and a grant from the Priority Research Centers Program through NRF funded by MEST (No. 2010-0020089).

References

NOTES

^*Corresponding author.