Open Journal of Fluid Dynamics
Vol.04 No.04(2014), Article ID:52383,23 pages
10.4236/ojfd.2014.44029
A Computational Study of the Transformation of Global Gas Flows in the Earth’s Atmosphere over the Course of a Year
Igor V. Mingalev, Konstantin G. Orlov, Victor S. Mingalev*
Polar Geophysical Institute of the Kola Scientific Center, Russian Academy of Sciences, Apatity, Murmansk Region, Russia
Email: *mingalev@pgia.ru
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 24 October 2014; revised 13 November 2014; accepted 12 December 2014
ABSTRACT
A mathematical model, developed earlier in the Polar Geophysical Institute, is applied to investi- gate the transformation of global gas flows in the Earth’s atmosphere over the course of a year. The model is based on the numerical solution of the system of gas dynamic equations. The mathe- matical model produces three-dimensional distributions of the gas dynamic parameters of the at- mosphere in the height range from 0 to 126 km over the Earth’s surface. To investigate the sea- sonal transformation of the global circulation of the lower and middle atmosphere, simulations are performed for conditions corresponding to twelve dates, which belong to twelve different months. Results of simulations indicate that the variations of the solar illumination of the Earth’s atmosphere, conditioned by different positions of the Earth along its trajectory around the Sun, influence considerably the transformation of the planetary circulation of the lower and middle atmosphere over the course of a year.
Keywords:
Numerical Simulation, Air Flow, Lower and Middle Atmosphere

1. Introduction
Fluid dynamics may be successfully applied for solving problems of environmental sciences. To investigate gas flows in the Earth’s atmosphere with the help of the fluid dynamics, not only the theoretical and experimental but also computational studies may be applied. Several general circulation models of the lower and middle atmosphere have been developed during the last three decades (for example, see [1] - [12] ). It can be noticed that the bulk of these models are hydrostatic. Usually, the hydrostatic models include the pressure coordinate equations of atmospheric dynamic meteorology, with the vertical velocity being obtained with the help of a simple hydrostatic equation.
Not long ago, a non-hydrostatic mathematical model of the global neutral wind system of the Earth’s atmosphere has been developed in the Polar Geophysical Institute (PGI) [13] [14] . This model enables to calculate three-dimensional global distributions of the zonal, meridional and vertical components of the neutral wind at levels of the troposphere, stratosphere, mesosphere and lower thermosphere, with whatever restrictions on the vertical transport of the neutral gas being absent. Therefore, the model is non-hydrostatic. The characteristic feature of the model is that the model does not include the internal energy equation for the neutral gas. Instead, the global temperature field is assumed to be a given distribution obtained from the NRLMSISE-00 empirical model [15] .
This non-hydrostatic mathematical model has been utilized in order to investigate numerically how the horizontal non-uniformity of the atmospheric gas temperature affects the formation of the middle atmosphere global circulation [13] [14] [16] [17] . Also, this model has been utilized in order to investigate numerically how solar activity and geomagnetic activity affect the formation of the large-scale global circulation of the mesosphere and lower thermosphere [18] [19] .
The purpose of the present work is to continue these studies with the help of the non-hydrostatic model of the global neutral wind system, developed earlier in the Polar Geophysical Institute, and to investigate numerically the seasonal variations of the global circulation of the Earth’s lower and middle atmosphere which take place over the course of a year.
2. Numerical Model
The utilized model differs from the bulk of existing global circulation models of the atmosphere, on principle. Firstly, the model does not include the pressure coordinate equations of atmospheric dynamic meteorology, in particular, the hydrostatic equation. Instead, the vertical component of the neutral wind velocity is obtained by means of a numerical solution of the appropriate momentum equation, with whatever simplifications of this equation being absent. Thus, three components of the neutral wind velocity are obtained by means of a numerical solution of the generalized Navier-Stokes equation.
Secondly, the model does not include the internal energy equation for the neutral gas. Instead, the global temperature field is assumed to be a given distribution. This peculiarity proceeds from complexity and uncertainty in various chemical-radiational heating and cooling rates, resulting in a discrepancy between the simulated and observed distributions of the atmospheric temperature. On the other hand, over the last years empirical models of the global atmospheric temperature field have been successfully developed. In the present study, we take the global temperature distribution from the NRLMSISE-00 empirical model [15] and consider it to be an input parameter of the model.
The utilized model produces three-dimensional global distributions of the zonal, meridional, and vertical components of the neutral wind velocity and neutral gas density at the levels of the troposphere, stratosphere, mesosphere, and lower thermosphere. The model has the potential to describe the global neutral wind system under disturbed conditions when the vertical component of the neutral wind velocity at the levels of the lower thermosphere can be as large as several tens of meters per second [20] -[22] .
The mathematical model, utilized in the present study, is based on the numerical solution of the system of equations containing the dynamical equation and continuity equation for the neutral gas. For solving the system of equations, the finite-difference method is applied. The dynamical equation for the neutral gas in vectorial form can be written as
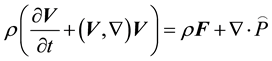 (1)
(1)
where 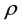 is the neutral gas density,
is the neutral gas density, 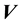 is the neutral wind velocity,
is the neutral wind velocity,  is the acceleration comprising the gravity acceleration, Coriolis acceleration, acceleration of translation, and acceleration due to elastic collisions with the ion gas, and
is the acceleration comprising the gravity acceleration, Coriolis acceleration, acceleration of translation, and acceleration due to elastic collisions with the ion gas, and 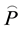 is the total stress tensor. The acceleration
is the total stress tensor. The acceleration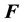 , consisting of four parts, can be written as (for example, see [23] )
, consisting of four parts, can be written as (for example, see [23] )
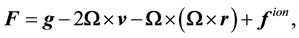 (2)
(2)
where 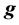 is the gravity acceleration,
is the gravity acceleration,  is the Earth’s angular velocity,
is the Earth’s angular velocity,  is a radius vector from the center of the Earth to the point where the equation is applied, and
is a radius vector from the center of the Earth to the point where the equation is applied, and 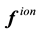 is the acceleration due to elastic collisions with the ion gas. The total stress tensor
is the acceleration due to elastic collisions with the ion gas. The total stress tensor  can be decomposed as follows:
can be decomposed as follows:
 (3)
(3)
where 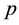 is the pressure,
is the pressure, 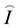 is the unit tensor, and
is the unit tensor, and 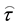 is the extra stress tensor.
is the extra stress tensor.
In the mathematical model, utilized in the present study, we use a spherical coordinate system







where 















The former tensor, 

where 


where 



The utilized mathematical model contains the continuity equation of the neutral gas which can be written as

Besides, the state equation for an ideal gas is used in the utilized mathematical model for obtaining the con- nection between the pressure and temperature of the neutral gas.
The system of equations containing the momentum equations for the vertical, meridional, and zonal components of the neutral gas velocity, Equations (4)-(6), as well as the continuity equation, Equation (10), is nu- merically solved in a layer surrounding the Earth globally. The lower boundary of this layer is the Earth’s surface, which is assumed to be an oblate spheroid whose radius at the equator is more than that at the pole. The upper boundary of this layer is the sphere lain at the altitude of 126 km at the equator.
At the lower boundary, the velocity vector is determined from the no-slip conditions on the ground. Simulation results to be presented in this paper are obtained using the following condition at the upper boundary:

The utilized mathematical model allows us to calculate three-dimensional global distributions of the vertical, meridional, and zonal components of the neutral wind and neutral gas density. As pointed out previously, the finite-difference method is applied for solving the system of equations. Complete details of the utilized finite-difference method and numerical schemes have been presented in the paper of Mingalev et al. [25] . The effect of the turbulence on the mean flow is taken into account by using the empirical subgrid-scale parameterization. The calculated parameters are determined on a 1˚ grid in both longitude and latitude. The height step is non-uniform and does not exceed the value of 1 km . More complete details of the utilized mathematical model can be found in the studies of Mingalev and Mingalev [13] and Mingalev et al. [14] .
3. Simulation Results and Discussion
The utilized mathematical model of the global neutral wind system can be used for different solar illumination and geomagnetic conditions. To investigate the seasonal transformation of the global circulation of the lower and middle atmosphere, simulations are performed for conditions corresponding to twelve dates, which belong to twelve different months. These dates are 16 January, 16 February, 16 March, 16 April, 16 May, 16 June, 16 July, 16 August, 16 September, 16 October, 16 November, and 16 December. For each enumerated day, calculations were performed for identical solar cycle and geomagnetic conditions, namely, for moderate solar activity (F10.7 = 101) and low geomagnetic activity (Kp = 1). The variations of the atmospheric parameters with time were calculated until they become stationary. The steady-state distributions of the atmospheric parameters were obtained for twelve considered dates on condition that inputs to the model are time-independent and correspondent to the identical moment (10.30 UT) for each day. The temperature distributions, corresponding to this moment, were taken for each day from the NRLMSISE-00 empirical model [15] .
Firstly, we made model calculations for the period from winter to summer in the northern hemisphere (from January to June). Secondly, the transformation of the global circulation of the lower and middle atmosphere was calculated for the period from summer to winter in the northern hemisphere (from July to December). Since the calculated transformations turned out different, it is convenient to present them separately.
3.1. Simulation Results for the Period from January to June
In the present subsection, the numerical model is applied to simulate the global distributions of the atmospheric parameters in the lower and middle atmosphere for conditions corresponding to six dates, which belong to six different months beginning from January. The steady-state distributions of the atmospheric parameters were calculated for six considered dates on condition that inputs to the model correspond to 10.30 UT for each day. The obtained simulation results are shown in Figures 1-8. The given temperature distributions, obtained for the altitude of 50 km , are shown on the top panels of Figures 1-6. It is seen that the planetary distributions of the atmospheric temperature are non-uniform and distinct in different months. Their distinctions are conditioned by different conditions of solar illumination of the Earth’s atmosphere. It is seen that the distinctions between temperatures, obtained for different considered months, can achieve a few tens of degrees at identical points of the globe.
Let us consider global distributions of the horizontal and vertical wind for conditions corresponding to six dates, which belong to six different months (Figures 1-6). Three-dimensional global distributions of the horizontal and vertical components of the neutral wind velocity, calculated with the help of the mathematical model, illustrate both common characteristic features and distinctions caused by various conditions of solar illumination.
The calculated global atmospheric circulations possess the following common features. The horizontal and vertical components of the wind velocity are changeable functions not only of latitude and longitude but also of altitude. Maximal absolute values of the horizontal and vertical components of the wind velocity are larger at higher altitudes. Horizontal domains exist where the steep gradients in the horizontal velocity field take place. The horizontal wind velocity can have various directions which may be opposite at the near points, displaced for a distance of a few steps of finite-difference approximation. Moreover, horizontal domains exist in which the vertical neutral wind component has opposite directions. As a rule, the horizontal domains, where the vertical neutral wind component is upward, are significantly extended in both latitude and longitude. On the contrary, horizontal domains having a downward vertical neutral wind component are extended in longitude but narrow in latitude. Usually, the latter domains have a configuration like a long narrow band and coincide, as a rule, with the regions, where the steep gradients in the horizontal velocity field take place. Maximal absolute values of the upward vertical wind component are less than the maximal module of the downward vertical wind component. The vertical wind velocity can achieve values of a few m/s at levels of the lower thermosphere in the horizontal domains having a configuration like a limited narrow band. At levels of the middle atmosphere, the horizontal wind velocity can achieve values of more than 100 m/s.
Let us consider simulation results, obtained for different months, and their distinctions. From Figure 1 one can see that, for winter period in the northern hemisphere, at levels of the middle atmosphere, the horizontal motion of the neutral gas is primarily eastward in the northern hemisphere and primarily westward in the southern hemisphere. On the contrary, from Figure 6, it is seen that, for the summer period in the northern hemisphere, the directions of these motions are opposite in both hemispheres.
It is know that the global atmospheric circulation can contain sometimes so called circumpolar vortices that are the largest scale inhomogeneities in the global neutral wind system. Their extent can be very large, sometimes reaching the latitudes close to the equator. It is well known from numerous observations that circumpolar vortices are formed at heights of the stratosphere and mesosphere in the periods close to summer and winter solstices, when there is no rebuilding of the atmosphere. The circumpolar anticyclone arises in the northern hemisphere under summer conditions, while the circumpolar cyclone arises in the southern hemisphere under winter conditions. On the contrary, the circumpolar cyclone arises in the northern hemisphere under winter conditions, while the circumpolar anticyclone arises in the southern hemisphere under summer conditions. Let us compare these experimental data with the simulation results, obtained for January and June conditions.
Figure 1. The distributions of the given neutral gas temperature (top panel), vector of the calculated horizontal component of the neutral wind velocity (middle panel), and calculated vertical component of the neutral wind velocity (bottom panel) as functions of longitude and latitude at the altitude of 50 km , obtained for 16 January. The temperature is given in K and wind velocities are given in m/s, with positive direction of the vertical component being upward.
Figure 2. The same as in Figure 1 but obtained for 16 February.
Figure 3. The same as in Figure 1 but obtained for 16 March.
Figure 4. The same as in Figure 1 but obtained for 16 April.
Figure 5. The same as in Figure 1 but obtained for 16 May.
Figure 6. The same as in Figure 1 but obtained for 16 June.
Figure 7. The temporal evolution of the zonal component of the neutral wind derived from simulation results for the point of the glob having the geographical coordinates of 45˚N and 22.5˚E (northern hemisphere, noon meridian) at three altitudes: 30, 50 and 70 km .
Figure 8. The same as in Figure 7 but obtained for the point of the glob having the geographical coordinates of 45˚S and 22.5˚E (southern hemisphere, noon meridian).
From Figure 1, one can see that a circumpolar cyclone is formed in the winter period in the northern hemisphere (the motion of the neutral gas is primarily eastward), and a circumpolar anticyclone is formed in the summer in the southern hemisphere (the motion of the neutral gas is primarily westward). It can be noticed that the center of the northern cyclone is displaced from the pole by approximately 10˚ in latitude.
From Figure 6, one can see that a circumpolar anticyclone is formed in the summer period in the northern hemisphere (the motion of the neutral gas is primarily westward), and a circumpolar cyclone is formed in the winter in the southern hemisphere (the motion of the neutral gas is primarily eastward). It is easy to see that the circumpolar vortices of the northern and southern hemispheres, obtained using the mathematical model at the level of the middle atmosphere for January and June conditions, correspond qualitatively to the global circulation, obtained from observations.
Incidentally, the qualitative agreement between January and June circulations of the middle atmosphere, obtained numerically and experimentally, manifests the adequacy of the distributions of atmospheric temperature, taken from the NRLMSISE-00 empirical model [15] and utilized in the numerical model.
From Figure 2, one can see that the calculated global atmospheric circulation in February is similar to that calculated in January. From Figure 3, it can be seen that the calculated atmospheric circulation in the southern hemisphere in March begins to transform considerably. Analogous transformation of the calculated atmospheric circulation in the northern hemisphere begins in April (Figure 4). From Figure 5, one can see that the calculated global atmospheric circulation in May is similar to that calculated in June. Thus, during March and April, at the levels of stratosphere and mesosphere, circumpolar vortices of the atmosphere transform significantly, with the direction of the flow becoming opposite. This transformation is illustrated by Figure 7 and Figure 8, from which one can see that the process of the transformation of the global atmospheric circulation arises in the mesosphere and continues in the stratosphere.
3.2. Simulation Results for the Period from July to December
In the present subsection, the numerical model is applied to simulate the global distributions of the atmospheric parameters in the lower and middle atmosphere for the period from summer to winter in the northern hemisphere (from July to December). Calculations were made for conditions corresponding to six dates, which belong to six different months beginning from July. In Figures 9-16, simulation results, obtained for six different months on condition that the inputs to the model and boundary conditions are time-independent and correspondent to 10.30 UT for each day, are shown. Three-dimensional global distributions of the horizontal and vertical components of the neutral wind velocity, calculated with the help of the mathematical model, illustrate both common characteristic features and distinctions caused by various conditions of solar illumination.
In essence, the common characteristic features are the same as in the previous subsection, describing the results for the period from January to June. In particular, the distinctions between given temperatures, obtained for different considered months, can achieve a few tens of degrees at identical points of the globe. It is seen that horizontal non-uniformity of the atmospheric temperature, which is distinct in different months, influences considerably on the transformation of global circulation of the lower and middle atmosphere during the period from July to December.
Let us consider simulation results, obtained for different months, and their distinctions. From simulation results, we can see that the global distributions of the neutral wind, calculated for July conditions, in particular, the large-scale circumpolar vortices, are qualitatively similar to those, calculated for June conditions and discussed in the previous subsection. It can be seen that the global distributions of the neutral wind, calculated for December conditions, in particular, the large-scale circumpolar vortices, are qualitatively similar to those, calculated for January conditions and discussed in the previous subsection. It may be recalled that these large-scale circumpolar vortices correspond qualitatively to those, obtained from observations.
Let us consider the process of transformation of the global circulation of the lower and middle atmosphere during the period from July to December. The global atmospheric circulation, computed for August conditions, is similar to that, calculated for July conditions, with maximal absolute values of the horizontal component of the wind velocity being less in August than in July.
In the northern hemisphere, in September, at the levels of stratosphere and mesosphere, the module of the neutral gas velocity is reduced but the direction of the flow remains just the same (circumpolar anticyclone). Unlike, at the levels close to the stratopause (approximately 50 km ), the direction of the flow becomes contrary
Figure 9. The distributions of the given neutral gas temperature (top panel), vector of the calculated horizontal component of the neutral wind velocity (middle panel), and calculated vertical component of the neutral wind velocity (bottom panel) as functions of longitude and latitude at the altitude of 50 km , obtained for 16 July. The temperature is given in K and wind velocities are given in m/s, with positive direction of the vertical component being upward.
Figure 10. The same as in Figure 9 but obtained for 16 August.
Figure 11. The same as in Figure 9 but obtained for 16 September.
Figure 12. The same as in Figure 9 but obtained for 16 October.
Figure 13. The same as in Figure 9 but obtained for 16 November.
Figure 14. The same as in Figure 9 but obtained for 16 December.
Figure 15. The temporal evolution of the zonal component of the neutral wind derived from simulation results for the point of the glob having the geographical coordinates of 45˚N and 22.5˚E (northern hemisphere, noon meridian) at three altitudes: 30, 50, and 70 km .
Figure 16. The same as in Figure 15 but obtained for the point of the glob having the geographical coordinates of 45˚S and 22.5˚E (southern hemisphere, noon meridian).
(circumpolar cyclone). In October, in the northern hemisphere, at the levels close to the stratopause, the circumpolar cyclone increases; at the levels of stratosphere and mesosphere the direction of the flow becomes opposite, with the circumpolar cyclone arising. Thus, during September, in the northern hemisphere, at the levels of stratosphere and mesosphere, circumpolar vortices of the atmosphere changes significantly, with the direction of the flow becoming opposite.
In the southern hemisphere, the period of rebuilding of circumpolar vortices begins in September and lasts during October, with the process starting in the mesosphere and continuing in the stratosphere.
In November, in both hemispheres, the circumpolar vortices increase and, to December, they become analogous to those observed usually in the period close to the winter solstice.
Thus, during August and September, at the levels of stratosphere and mesosphere, circumpolar vortices of the atmosphere transform significantly, with the direction of the flow becoming opposite. This transformation is illustrated in Figure 15 and Figure 16.
During the period from July to December, at the levels of 60 km , maximal absolute value of the horizontal component of the wind velocity in both hemispheres ought to be biggest in July, and that ought to be least in August.
4. Summary and Concluding Remarks
To investigate the transformations of the global circulation of the lower and middle atmosphere, conditioned by changing solar illumination of the Earth’s atmosphere over the course of a year, the mathematical non-hydrostatic model of the global neutral wind system of the atmosphere, developed earlier in the Polar Geophysical Institute, was utilized. One of the peculiarities of the utilized model consists in using the global temperature field as a given distribution, i.e., the input parameter of the numerical model. The global temperature field is taken from the NRLMSISE-00 empirical model [15] . The utilized mathematical model, based on the numerical solution of the system of gas dynamic equations, produces three-dimensional distributions of the gas dynamic parameters of the atmosphere in the height range from 0 to 126 km over the Earth’s surface.
By means of the mathematical model, the steady-state distributions were obtained of the atmospheric parameters corresponding to 16 January, 16 February, 16 March, 16 April, 16 May, 16 June, 16 July, 16 August, 16 September, 16 October, 16 November, and 16 December (all at 10.30 UT). For each enumerated day, calculations were performed for identical solar cycle and geomagnetic conditions, namely, for moderate solar activity and low geomagnetic activity.
Simulation results indicate that, for all months, the horizontal and vertical components of the wind velocity are changeable functions not only of latitude and longitude but also of altitude. Horizontal domains exist where the steep gradients in the horizontal velocity field take place. Moreover, horizontal domains exist in which the vertical neutral wind component has opposite directions. As a rule, the horizontal domains, where the vertical neutral wind component is upward, are significantly extended in both latitude and longitude. On the contrary, horizontal domains having a downward vertical neutral wind component are extended in longitude but narrow in latitude.
The results of simulation indicated that the process of transformation of the global circulation of the lower and middle atmosphere during the period from January to June possesses the following peculiarities. In the northern hemisphere, the circulation, characteristic for period close to winter solstice, ought to exist up to April. During April this circulation is weakened and a circulation, characteristic for period close to summer solstice, arises. From May to June, the arisen circulations ought to increase. An analogous transformation takes place in the southern hemisphere during the past half of March and April. The process of the transformation of the global atmospheric circulation arises in the mesosphere and then propagates downward.
The results of simulation indicated that the process of transformation of the global circulation of the lower and middle atmosphere during the period from July to December possesses the following peculiarities. In the northern hemisphere, the circulation, characteristic for period close to summer solstice, ought to exist up to September. During September this circulation is weakened and a circulation, characteristic for period close to winter solstice, arises. This transformation ought to begin from the level of the stratopause and then to propagate upward and downward. An analogous transformation takes place in the southern hemisphere during the past half of September and October. This transformation ought to begin from the level of the mesosphere and then to propagate downward. From November to December, the arisen circulations ought to increase.
To understand the cause of the significant transformation of global gas flows in the Earth’s atmosphere over the course of a year, obtained numerically in the present study, it is useful to take into account the following circumstances. It is obvious that the horizontal non-uniformity of the neutral gas temperature, which is distinct in different months, influences considerably on the transformation of global circulation of the lower and middle atmosphere. It is clear that the global temperature field depends on changing solar illumination of the Earth’s atmosphere over the course of a year. It is well known that the Earth has an elliptical orbit, with the rotational axis of the Earth having a tilt of about 67˚ to the orbit plane (Figure 17). In the northern hemisphere, the winter solstice occurs on about 22 December, summer solstice is near 22 June, spring equinox is around 21 March and autumnal equinox is about 23 September. In the southern hemisphere, the axial tilt is exactly the opposite of the direction in the northern hemisphere. Thus the seasonal effects in the south are reversed.
When the northern pole is tilted toward the Sun the day lasts longer. This results in warmer average temperatures from the increase in solar radiation reaching the surface. When the northern pole is tilted away from the Sun, the reverse is true and the climate is generally cooler. Above the Arctic Circle, an extreme case is reached where there is no daylight at all for part of the year. This effect is called a polar night. The variations in solar radiation reaching the surface (because of the direction of the Earth’s axial tilt) results in the seasons.
The ellipticity of the Earth’s orbit leads to changes of the Sun-Earth distance over the course of a year. The changing Sun-Earth distance results in an increase of about 7% in solar energy reaching the Earth at perihelion relative to aphelion. Earth’s perihelion occurs around 3 January, and the aphelion around 4 July. Since the southern hemisphere is tilted toward the Sun at about the same time that the Earth reaches the closest approach to the Sun, the southern hemisphere receives slightly more energy from the Sun than does the northern over the course of a year.
Thus, different positions of the Earth along its trajectory around the Sun, in particular the changing Sun-Earth distance, ought to affect the formation of the global atmospheric temperature field in the lower and middle atmosphere. It may be recalled that, in the utilized mathematical model, we take the global temperature distribution from the NRLMSISE-00 empirical model [15] and consider it to be an input parameter of the numerical model. It is essential that the NRLMSISE-00 empirical model represents the dependence of the global atmospheric temperature field on different positions of the Earth along its trajectory around the Sun due to the fact that
Figure 17. An exaggerated representation of the shape of Earth’s orbit. The solstices are the points in the orbit of maximum axial tilt toward or away from the Sun. The equinoxes are the points in the orbit, when the direction of the tilt and the direction to the Sun are perpendicular.
the date and universal time (UT) are the input parameters of the latter empirical model.
As pointed out previously, the circumpolar vortices of the northern and southern hemispheres, obtained using the applied mathematical model at levels of the lower and middle atmosphere, are consistent with existing observational data, in particular, for winter and summer periods. Therefore, this fact manifests the adequacy of the distributions of the atmospheric temperature, calculated with the help of the NRLMSISE-00 empirical model [15] and utilized in our simulations.
It can be noted that modern scientific facility does not allow somebody to measure global three-dimensional fields of gas dynamical parameters, in particular global neutral wind system, of the lower and middle atmosphere at the same time, unfortunately. On the other hand, scientific researches, prediction applications and other environmental activities are in need of the planetary neutral wind systems for various geophysical conditions. The global neutral wind systems, obtained with the help of computational studies, in particular the simulation results, obtained in the present study for twelve different months, may be useful for these activities.
Acknowledgements
This work was partly supported by Grant No. 13-01-00063 from the Russian Foundation for Basic Research.
References
- Manabe, S. and Hahn, D.G. (1981) Simulation of Atmospheric Variability. Monthly Weather Review, 109, 2260-2286. http://dx.doi.org/10.1175/1520-0493(1981)109<2260:SOAV>2.0.CO;2
- Cariolle, D., Lasserre-Bigorry, A., Royer, J.F. and Geleyn J.F. (1990) A General Circulation Model Simulation of the Springtime Antarctic Ozone Decrease and Its Impact on Mid-Latitudes. Journal of Geophysical Research, 95, 1883- 1898. http://dx.doi.org/10.1029/JD095iD02p01883
- Rasch, P.J. and Williamson, D.L. (1991) The Sensitivity of a General Circulation Model Climate to the Moisture Transport Formulation. Journal of Geophysical Research, 96, 13123-13137. http://dx.doi.org/10.1029/91JD01179
- Graf, H.F., Kirchner, I., Sausen, R. and Schubert, S. (1992) The Impact of Upper-Tropospheric Aerosol on Global Atmospheric Circulation. Annales Geophysicae, 10, 698-707.
- Stott, P.A. and Harwood, R.S. (1993) An Implicit Time-Stepping Scheme for Chemical Species in a Global Atmospheric Circulation Model. Annales Geophysicae, 11, 377-388.
- Christiansen, B., Guldberg, A., Hansen, A.W. and Riishojgaard, L.P. (1997) On the Response of a Three-Dimensional General Circulation Model to Imposed Changes in the Ozone Distribution. Journal of Geophysical Research, 102, 13051-13077. http://dx.doi.org/10.1029/97JD00529
- Galin, V.Y. (1997) Parametrization of Radiative Processes in the DNM Atmospheric Model. Izvestiya AN, Physics of Atmosphere and Ocean, 34, 380-389. (Russian Issue)
- Gibelin, A.L. and Deque, M. (2002) Anthropogenic Climate Change over the Mediterranean Region Simulated by a Global Variable Resolution Model. Climate Dynamics, 20, 327-339.
- Mendillo, M., Rishbeth, H., Roble, R.G. and Wroten, J. (2002) Modelling F2-Layer Seasonal Trends and Day-to-Day Variability Driven by Coupling with the Lower Atmosphere. Journal of Atmospheric and Solar-Terrestrial Physics, 64, 1911-1931. http://dx.doi.org/10.1016/S1364-6826(02)00193-1
- Harris, M.J., Arnold, N.F. and Aylward, A.D. (2002) A Study into the Effect of the Diurnal Tide on the Structure of the Background Mesosphere and Thermosphere Using the New Coupled Middle Atmosphere and Thermosphere (CMAT) General Circulation Model. Annales Geophysicae, 20, 225-235. http://dx.doi.org/10.5194/angeo-20-225-2002
- Langematz, U., Claussnitzer, A., Matthes, K. and Kunze, M. (2005) The Climate during Maunder Minimum: A Simulation with Freie Universitat Berlin Climate Middle Atmosphere Model (FUB-CMAT). Journal of Atmospheric and Solar-Terrestrial Physics, 67, 55-69. http://dx.doi.org/10.1016/j.jastp.2004.07.017
- Smith, A.K., Garcia, R.R., Marsh, D.R. and Richter, J.H. (2011) WACCM Simulations of the Mean Circulation and Trace Species Transport in the Winter Mesosphere. Journal of Geophysical Research, 116, Article ID: D20115, 17 p.
- Mingalev, I.V. and Mingalev, V.S. (2005) The Global Circulation Model of the Lower and Middle Atmosphere of the Earth with a Given Temperature Distribution. Mathematical Modeling, 17, 24-40. (In Russian)
- Mingalev, I.V., Mingalev, V.S. and Mingaleva, G.I. (2007) Numerical Simulation of Global Distributions of the Horizontal and Vertical Wind in the Middle Atmosphere Using a Given Neutral Gas Temperature Field. Journal of Atmospheric and Solar-Terrestrial Physics, 69, 552-568. http://dx.doi.org/10.1016/j.jastp.2006.10.005
- Picone, J.M., Hedin, A.E., Drob, D.P. and Aikin, A.C. (2002) NRLMSISE-00 Empirical Model of the Atmosphere: Statistical Comparisons and Scientific Issues. Journal of Geophysical Research, 107, Article ID: 1468, 16 p.
- Mingalev, I.V., Mingalev, O.V. and Mingalev, V.S. (2008) Model Simulation of Global Circulation in the Middle Atmosphere for January Conditions. Advances in Geosciences, 15, 11-16. http://dx.doi.org/10.5194/adgeo-15-11-2008
- Mingalev, I.V., Mingalev, V.S. and Mingaleva, G.I. (2012) Numerical Simulation of the Global Neutral Wind System of the Earth’s Middle Atmosphere for Different Seasons. Atmosphere, 3, 213-228. http://dx.doi.org/10.3390/atmos3010213
- Mingalev, I.V. and Mingalev, V.S. (2012) Numerical Modeling of the Influence of Solar Activity on the Global Circulation in the Earth’s Mesosphere and Lower Thermosphere. International Journal of Geophysics, 2012, Article ID: 106035, 15 p.
- Mingalev, I., Mingaleva, G. and Mingalev, V. (2013) A Simulation Study of the Effect of Geomagnetic Activity on the Global Circulation in the Earth’s Middle Atmosphere. Atmospheric and Climate Sciences, 3, 8-19. http://dx.doi.org/10.4236/acs.2013.33A002
- Wardill, P. and Jacka, F. (1986) Vertical Motions in the Thermosphere over Mawson, Antarctica. Journal of Atmospheric and Terrestrial Physics, 48, 289-292. http://dx.doi.org/10.1016/0021-9169(86)90104-2
- Crickmore, R.I., Dudeney, J.R. and Rodger, A.S. (1991) Vertical Thermospheric Winds at the Equatorward Edge of the Auroral Oval. Journal of Atmospheric and Terrestrial Physics, 53, 485-492. http://dx.doi.org/10.1016/0021-9169(91)90076-J
- Ishii, M. (2005) Relationship between Thermospheric Vertical Wind and the Location of Ionospheric Current in the Polar Region. Advances in Polar Upper Atmosphere Research, 19, 63-70.
- Mingalev, V.S. (1993) Transport Equations for the Upper Atmosphere in a Rotating Reference Frame. Geomagnetizm i Aeronomiya, 33, 106-112. (Russian Issue)
- Obukhov, A.M. (1988) Turbulence and Dynamics of Atmosphere. Hydrometeoizdat, Leningrad. (In Russian)
- Mingalev, V.S., Mingalev, I.V., Mingalev, O.V., Oparin, A.M. and Orlov, K.G. (2010) Generalization of the Hybrid Monotone Second-Order Finite Difference Scheme for Gas Dynamics Equations to the Case of Unstructured 3D Grid. Computational Mathematics and Mathematical Physics, 50, 877-889. http://dx.doi.org/10.1134/S0965542510050118
NOTES
*Corresponding author.



















