Open Journal of Fluid Dynamics
Vol.04 No.03(2014), Article ID:49695,9 pages
10.4236/ojfd.2014.43022
DNS Analysis on the Indirect Relationship between the Local Burning Velocity and the Flame Displacement Speed of Turbulent Premixed Flames
Kazuya Tsuboi, Eiji Tomita
Graduate School of Natural Science and Technology, Okayama University, Okayama, Japan
Email: tsuboi@okayama-u.ac.jp
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 16 June 2014; revised 18 July 2014; accepted 21 July 2014
ABSTRACT
The local burning velocity and the flame displacement speed are the dominant properties in the mechanism of turbulent premixed combustion. The flame displacement speed and the local burning velocity have been investigated separately, because the flame displacement speed can be used for the discussion of flame-turbulence interactions and the local burning velocity can be used for the discussion of the inner structure of turbulent premixed flames. In this study, to establish the basis for the discussion on the effects of turbulence on the inner structure of turbulent premixed flames, the indirect relationship between the flame displacement speed and the local burning velocity was investigated by the flame stretch, the flame curvature, and the tangential strain rate using DNS database with different density ratios. It was found that for the local tangential strain rate and the local flame curvature, the local burning velocity and the flame displacement speed had the opposite correlations in each density ratio case. Therefore, it is considered that the local burning velocity and the flame displacement speed have a negative correlation.
Keywords:
Local Burning Velocity, Flame Displacement Speed, Flame Stretch Rate, Tangential Strain Rate, Flame Curvature, Turbulent Premixed Flame, Direct Numerical Simulation

1. Introduction
Since the late 20th century, the possibilities of the exhaustion of fossil fuels and the alternative fuels have been discussed. In the beginning of the 21st century, however, the fossil fuels still remain the main source of energy and it can be predicted easily that the current situation will be running for at least several decades. Therefore, further enhancement of the efficiency and reduction of the environmental load are required for the combustion technology. In many combustors, turbulent combustion is mainly utilized. The local burning velocity and the flame displacement speed are the dominant properties in the mechanism of turbulent premixed combustion. The local burning velocity is the instantaneous local quantity based on the local consumption rate of an unburned mixture, while the flame displacement speed is the local quantity based on the flame normal speed, in which the flame surface, defined as the isosurface of temperature or mass fraction of an unburned mixture, moves relatively to a local flow [1] . Burning velocity should be essentially the quantity based on the chemical reaction rate because combustion is a kind of chemical reactions. Thus, the local burning velocity is considered to be the most appropriate burning velocity in turbulent premixed combustion in terms of the definition. The local burning velocity can be evaluated both theoretically and numerically; however, it is almost impossible to obtain the local burning velocity experimentally using the current technology of measurement. In addition, the flame displacement speed can be evaluated both theoretically and numerically more easily than the local burning velocity. Therefore, the flame displacement speed has been utilized not only experimentally [2] - [8] but also numerically [9] - [22] . On the other hand, the local burning velocity has been performed numerically to analyze statistically the correlations between the flame stretch rate and its elements―the tangential strain rate, the flame curvature― for the clarification of the local structure of turbulent premixed flames by Haworth and Poinsot [23] , Rutland and Trouvé [24] , and subsequently by others [12] [22] [25] - [28] .
The flame displacement speed and the local burning velocity have been investigated separately, because the flame displacement speed can be used for the discussion of flame-turbulence interactions and the local burning velocity can be used for the discussion of the inner structure of turbulent premixed flames. In this study, to establish the basis for the discussion on the effects of turbulence on the inner structure of turbulent premixed flames, the indirect relationship between the flame displacement speed and the local burning velocity was investigated by the flame stretch, the flame curvature, and the tangential strain rate using DNS database with different density ratios.
2. Numerical Analysis Method
2.1. DNS Database
DNS database with different density ratios ρu/ρb was used for the analysis of both the local burning velocity and the flame displacement speed. These database were ρu/ρb = 2.50, termed case Lm; ρu/ρb = 5.00, termed case Mm; and ρu/ρb = 7.53, termed case Hm. The simulations were carried out on the VPP700 installed at RIKEN [29] -[32] . Details of the databases are given in Table 1. The computational domain is shown in Figure 1. The governing equations for constructing the database were the conservation of mass, chemical species, energy, and momentum (compressible Navier-Stokes equations), and the equation of state for an ideal gas. The database was constructed using a sixth-order central finite difference scheme in the mean flow direction and a Fourier spectral
Table 1. The DNS database.
Figure 1. Computational domain.
collocation scheme in the directions perpendicular to the mean flow for spatial discretisation. A third-order three-step Runge-Kutta method was used for the time evolution and an overall single-step irreversible reaction, which was the Arrhenius type, was used to describe the chemical kinetics. The inflow and outflow boundaries were described on the basis of Navier-Stokes characteristic boundary conditions (NSCBC) [33] [34] , and the lateral boundaries were periodic. The computational domain was 8 mm in the mean flow direction and 4 mm in the directions perpendicular to the mean flow; 512 and 128 grid points were used in the respective directions. At the inflow boundary, preliminary calculated homogeneous isotropic turbulence with a cycle of several milliseconds was used, with a mean inflow velocity assuming Taylor’s hypothesis of frozen turbulence with a phase shift.
Initially, a laminar premixed flame was formed, which grew to form a turbulent premixed flame. The inflow velocity of the unburned mixture was adjusted while monitoring the turbulent burning velocity until the turbulent premixed flame became fully developed and stabilised. The instantaneous turbulent burning velocity varied temporally; however, the time-averaged turbulent burning velocity, which can be measured experimentally, was steady. The database was constructed without changing the inflow velocity. Each case in the database consisted of almost 200 sampled data points at 51.68 μs intervals (which was longer than the DNS time step). The conditions described in the database correspond to the boundary between wrinkled flamelets and corrugated flamelets in the turbulent combustion regime diagram [35] . Further details of the calculation method to construct the DNS database can be found in Nishiki et al. [29] - [31] and Nishiki [32] .
2.2. Definitions of Local Burning Velocity and Flame Displacement Speed
A turbulent flame surface at each sampling time was identified as the isosurface of the prescribed reaction progress variable, cT, with which the reaction rate in the planar flame takes a maximum for each case in the database, i.e., cT = 0.89 for case Lm and cT = 0.90 for the other cases. The reaction progress variable is defined as:
 , (1)
, (1)
where T is the temperature, Ta is the adiabatic flame temperature, and Tu is the temperature of the unburned mixture (300 K). Typical shapes of the turbulent flame surface are shown in Figure 2.
The local burning velocity, uc, was evaluated at the flame surface as follows:
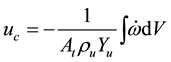 . (2)
. (2)
Substituting a normal to the local flame surface, n, for the infinitesimal volume, dV, Equation (2) can be rewritten as
 . (3)
. (3)
It follows that the local burning velocity can be evaluated by integrating the local reaction rate along the normal
Figure 2. Typical shapes of the turbulent premixed flame defined by the isosurface of the progress variable: c = 0.89 for the case Lm, and c = 0.90 for the other cases. From the top, we have cases Lm, Mm, and Hm. The figures in the left-hand-side column correspond to the minimum turbulent burning velocity uT, and those in the right-hand-side column correspond to the maximum uT for each case.
to the local flame surface. In the evaluation of the local burning velocity at a given point at the flame surface, the normal to the flame surface at the point may cross the flame surface at another point. To avoid this problem, we find the minimum distance of the normal between the point on the flame surface and the other point crossing the flame surface, and then obtain half of the distance between these points, as shown in Figure 3. For all the points where the flame surface intersected with the grid lines, the integration of Equation (3) was carried out within the obtained distance as one side of the integration range, which was at least the thickness of an unstretched flame, 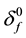 [27] .
[27] .
Using the balance equation of the reaction progress variable,
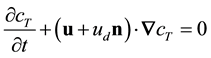 , (4)
, (4)
the flame displacement speed, ud, at each intersection on the flame surface is defined as:
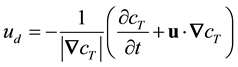 . (5)
. (5)
where n is the unit normal vector to the flame surface towards unburned mixture, u is the flow velocity vector.
Figure 3. Schematic of the integration range for the local burning velocity.
3. Results and Discussion
In order to evaluate the correlation between the local burning velocity and the flame displacement speed using the joint probability density function (joint pdf) appropriately, the both scales of the local burning velocity and the flame displacement speed must be the same. The local burning velocity is based on the consumption rate of the unburned mixture, and the flame displacement speed is based on the flame normal speed of the isosurface of the prescribed reaction progress variable defined as the flame surface. Thus, an equation of continuity:
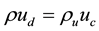 (6)
(6)
yields
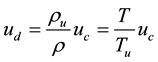 (7)
(7)
where ρ is the function of the reaction progress variable. In fact, the flame displacement speed is divided by T/Tu for the same scale of both the local burning velocity and the displacement speed. It is convenient, however, to substitute Tb for T because Tb can be measured easily in experiments when the DNS analysis is compared with experiments.
The local flame stretch rate, κ, which involves the local tangential strain rate, at, and local flame curvature, ∇×n, are defined as [36] [37] :
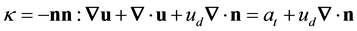 . (8)
. (8)
Joint pdfs of the local flame stretch rate with both the local burning velocity and flame displacement speed, which were reduced by 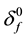 and
and
Joint pdfs of the local tangential strain rate with both the local burning velocity and flame displacement speed, which were reduced by 



From the observations above, the trend of the correlation between the local burning velocity and the flame stretch rate is caused by the facts that the local burning velocity has a very weakly negative correlation with the
Figure 4. Joint pdfs of the local flame stretch rate with both the local burning velocity (upper) and flame displacement speed (lower) for the different density ratios. From the left, case Lm, case Mm, and case Hm.
Figure 5. Joint pdfs of the local tangential strain rate with both the local burning velocity (upper) and flame displacement speed (lower) for the different density ratios. From the left, case Lm, case Mm, and case Hm.
Figure 6. Joint pdfs of the local flame curvature with both the local burning velocity (upper) and flame displacement speed (lower) for the different density ratios. From the left, case Lm, case Mm, and case Hm.
tangential strain rate and has a weakly positive correlation with the flame curvature for all density ratios. As for the correlation between the flame displacement speed and the flame stretch rate. For case Lm, the flame displacement speed had almost no correlation with the tangential strain rate and had a negative correlation with the flame curvature, as a result, these trends made the correlation between the flame displacement speed and the flame stretch rate negative. For case Mm and Hm, the flame displacement speed had weakly positive correlations with the tangential strain rate and had negative correlations with the flame curvature; as a result, these correlations lead to the insensitive trends of the flame displacement speed to the flmae stretch rate.
From the discussion above, for the tangential strain rate, the local burning velocity had very weakly negative correlations, while the flame displacement speed had almost positive correlations. For the flame curvature, the local burning velocity had weakly positive correlations, while the flame displacement speed had negative correlations. Therefore, it is considered that the local burning velocity and the flame displacement speed have a negative correlation under the conditions of this study.
4. Conclusion
The indirect relationship between the local burning velocity and the flame displacement speed was investigated using the DNS data of turbulent premixed flames with different density ratios. It was found that for the local tangential strain rate and the local flame curvature, the local burning velocity and the flame displacement speed had the opposite correlations in each density ratio case. Under the conditions of this study, it is considered that the local burning velocity and the flame displacement speed have a negative correlation.
References
- Poinsot, T., Echekki, T. and Mungal, M.G. (1992) A Study of the Laminar Flame Tip and Implications for Premixed Turbulent Combustion. Combustion Science and Technology, 81, 45-73. http://dx.doi.org/10.1080/00102209208951793
- Renou, B., Boukhalfa, A., Puechberty, D. and Trinité, M. (2000) Local Scalar Flame Properties of Freely Propagating Premixed Turbulent Flames at Various Lewis Numbers. Combustion and Flame, 123, 507-521. http://dx.doi.org/10.1016/S0010-2180(00)00180-2
- Kido, H., Nakahara, M., Nakashima, K. and Hashimoto, J. (2002) Influence of Local Flame Displacement Velocity on Turbulent Burning Velocity. Proceedings of the Combustion Institute, 29, 1855-1861. http://dx.doi.org/10.1016/S1540-7489(02)80225-5
- Gashi, S., Hult, J., Jenkins, K.W., Chakraborty, N., Cant, S. and Kaminski, C.F. (2005) Curvature and Wrinkling of Premixed Flame Kernels―Comparisons of OH PLIF and DNS Data. Proceedings of the Combustion Institute, 30, 809-817. http://dx.doi.org/10.1016/j.proci.2004.08.003
- Nakahara, M., Kido, H., Shirasuna, T. and Hirata, K. (2007) Effect of Stretch on Local Burning Velocity of Premixed Turbulent Flames. Journal of Thermal Science and Technology, 2, 268-280. http://dx.doi.org/10.1299/jtst.2.268
- Nakahara, M., Shirasuna, T. and Hashimoto, J. (2009) Experimental Study on Local Flame Properties of Hydrogen Added Hydrocarbon Premixed Turbulent Flames. Journal of Thermal Science and Technology, 4, 190-201. http://dx.doi.org/10.1299/jtst.4.190
- Tanahashi, M., Taka, S., Shimura, M. and Miyauchi, T. (2008) CH Double-Pulsed PLIF Measurement in Turbulent Premixed Flame. Experiments in Fluids, 45, 323-332. http://dx.doi.org/10.1007/s00348-008-0482-8
- Hartung, G., Hult, J., Balachandran, R., Mackley, M.R. and Kaminski, C.F. (2009) Flame Front Tracking in Turbulent Lean Premixed Flames Using Stereo PIV and Time-Sequenced Planar LIF of OH. Applied Physics B, 96, 843-862. http://dx.doi.org/10.1007/s00340-009-3647-0
- Echekki, T. and Chen, J.H. (1996) Unsteady Strain Rate and Curvature Effects in Turbulent Premixed Methane-Air Flames. Combustion and Flame, 106, 184-202. http://dx.doi.org/10.1016/0010-2180(96)00011-9
- Peters, N., Terhoeven, P., Chen, J.H. and Echekki, T. (1998) Statistics of Flame Displacement Speeds from Computations of 2-D Unsteady Methane-Air Flames. Proceedings of the Combustion Institute, 27, 833-839. http://dx.doi.org/10.1016/S0082-0784(98)80479-7
- Chen, J.H. and Im, H.G. (1998) Correlation of Flame Speed with Stretch in Turbulent Premixed Methane/Air Flames. Proceedings of the Combustion Institute, 27, 819-826. http://dx.doi.org/10.1016/S0082-0784(98)80477-3
- Chen, J.H. and Im, H.G. (2000) Stretch Effects on the Burning Velocity of Turbulent Premixed Hydrogen/Air Flames. Proceedings of the Combustion Institute, 28, 211-218. http://dx.doi.org/10.1016/S0082-0784(00)80213-1
- Im, H.G. and Chen, J.H. (2002) Preferential Diffusion Effects on the Burning Rate of Interacting Turbulent Premixed Hydrogen-Air Flames. Combustion and Flame, 131, 246-258. http://dx.doi.org/10.1016/S0010-2180(02)00405-4
- Hawkes, E.R. and Chen, J.H. (2004) Direct Numerical Simulation of Hydrogen-Enriched Lean Premixed Methane― Air Flames. Combustion and Flame, 138, 242-258. http://dx.doi.org/10.1016/j.combustflame.2004.04.010
- Chakraborty, N. and Cant, S. (2004) Unsteady Effects of Strain Rate and Curvature on Turbulent Premixed Flames in an Inflow-Outflow Configuration. Combustion and Flame, 137, 129-147. http://dx.doi.org/10.1016/j.combustflame.2004.01.007
- Chakraborty, N. and Cant, R.S. (2005) Influence of Lewis Number on Curvature Effects in Turbulent Premixed Flame Propagation in the Thin Reaction Zones Regime. Physics of Fluids, 17, 105105. http://dx.doi.org/10.1063/1.2084231
- Chakraborty, N. and Cant, R.S. (2006) Influence of Lewis Number on Strain Rate Effects in Turbulent Premixed Flame Propagation. International Journal of Heat and Mass Transfer, 49, 2158-2172. http://dx.doi.org/10.1016/j.ijheatmasstransfer.2005.11.025
- Chakraborty, N. (2007) Comparison of Displacement Speed Statistics of Turbulent Premixed Flames in the Regimes Representing Combustion in Corrugated Flamelets and Thin Reaction Zones. Physics of Fluids, 19, 105109. http://dx.doi.org/10.1063/1.2784947
- Chakraborty, N., Hartung, G., Katragadda, M. and Kaminski, C.F. (2011) Comparison of 2D and 3D Density-Weighted Displacement Speed Statistics and Implications for Laser Based Measurements of Flame Displacement Speed Using Direct Numerical Simulation Data. Combustion and Flame, 158, 1372-1390. http://dx.doi.org/10.1016/j.combustflame.2010.11.014
- Chakraborty, N., Klein, M. and Cant, R.S. (2007) Stretch Rate Effects on Displacement Speed in Turbulent Premixed Flame Kernels in the Thin Reaction Zones Regime. Proceedings of the Combustion Institute, 31, 1385-1392. http://dx.doi.org/10.1016/j.proci.2006.07.184
- Chakraborty, N., Klein, M. and Cant, R.S. (2011) Effects of Turbulent Reynolds Number on the Displacement Speed Statistics in the Thin Reaction Zones Regime of Turbulent Premixed Combustion. Journal of Combustion, 2011, Article ID: 473679. http://dx.doi.org/10.1155/2011/473679
- Han, I. and Huh, K.Y. (2008) Roles of Displacement Speed on Evolution of Flame Surface Density for Different Turbulent Intensities and Lewis Numbers in Turbulent Premixed Combustion. Combustion and Flame, 152, 194-205. http://dx.doi.org/10.1016/j.combustflame.2007.10.003
- Haworth, D.C. and Poinsot, T.J. (1992) Numerical Simulations of Lewis Number Effects in Turbulent Premixed Flames. Journal of Fluid Mechanics, 244, 405-436. http://dx.doi.org/10.1017/S0022112092003124
- Rutland, C.J. and Trouvé, A. (1993) Direct Simulations of Premixed Turbulent Flames with Nonunity Lewis Numbers. Combustion and Flame, 94, 41-57. http://dx.doi.org/10.1016/0010-2180(93)90018-X
- Hawkes, E.R. and Chen, J.H. (2006) Comparison of Direct Numerical Simulation of Lean Premixed Methane-Air Flames with Strained Laminar Flame Calculations. Combustion and Flame, 144, 112-125. http://dx.doi.org/10.1016/j.combustflame.2005.07.002
- Bell, J.B., Cheng, R.K., Day, M.S. and Shepherd, I.G. (2007) Numerical Simulation of Lewis Number Effects on Lean Premixed Turbulent Flames. Proceedings of the Combustion Institute, 31, 1309-1317. http://dx.doi.org/10.1016/j.proci.2006.07.216
- Tsuboi, K., Nishiki, S. and Hasegawa, T. (2008) An Analysis of Local Quantities of Turbulent Premixed Flames Using DNS Databases. Journal of Thermal Science and Technology, 3, 103-111. http://dx.doi.org/10.1299/jtst.3.103
- Day, M., Tachibana, S., Bell, J., Lijewski, M., Beckner, V. and Cheng, R.K. (2012) A Combined Computational and Experimental Characterization of Lean Premixed Turbulent Low Swirl Laboratory Flames: I. Methane Flames. Combustion and Flame, 159, 275-290. http://dx.doi.org/10.1016/j.combustflame.2011.06.016
- Nishiki, S., Hasegawa, T., Borghi, R. and Himeno, R. (2002) Analyzing and Modeling of Transport Properties of Turbulent Kinetic Energy and Turbulent Scalar Flux in Turbulent Premixed Flames by DNS. Journal of the Combustion Society of Japan, 48, 47-57.
- Nishiki, S., Hasegawa, T., Borghi, R. and Himeno, R. (2002) Modeling of Flame-Generated Turbulence Based on Direct Numerical Simulation Databases. Proceedings of the Combustion Institute, 29, 2017-2022. http://dx.doi.org/10.1016/S1540-7489(02)80246-2
- Nishiki, S., Hasegawa, T., Borghi, R. and Himeno, R. (2006) Modelling of Turbulent Scalar Flux in Turbulent Premixed Flames Based on DNS Databases. Combustion Theory and Modelling, 10, 39-55. http://dx.doi.org/10.1080/13647830500307477
- Nishiki, S. (2003) DNS and Modeling of Turbulent Premixed Combustion. Doctoral Thesis, Nagoya Institute of Technology, Nagoya.
- Poinsot, T.J. and Lele, S.K. (1992) Boundary Conditions for Direct Simulations of Compressible Viscous Flows. Journal of Computational Physics, 101, 104-129. http://dx.doi.org/10.1016/0021-9991(92)90046-2
- Baum, M., Poinsot, T. and Thévenin, D. (1995) Accurate Boundary Conditions for Multicomponent Reactive Flows. Journal of Computational Physics, 116, 247-261. http://dx.doi.org/10.1006/jcph.1995.1024
- Peters, N. (1999) The Turbulent Burning Velocity for Large-Scale and Small-Scale Turbulence. Journal of Fluid Mechanics, 384, 107-132. http://dx.doi.org/10.1017/S0022112098004212
- Williams, F.A. (1985) Combustion Theory. 2nd Edition, Benjamin Cummings, California.
- Candel, S.M. and Poinsot, T.J. (1990) Flame Stretch and the Balance Equation for the Flame Area. Combustion Science and Technology, 70, 1-15. http://dx.doi.org/10.1080/00102209008951608
Nomenclature
At: Turbulent flame area
at: Local tangential strain rate
cT: Reaction progress variable
Le: Lewis number
lt: Integral length scale
n: Normal to a flame surface
n: Unit normal vector to a flame surface towards unburned mixture


T: Temperature
u: Flow velocity
u: Flow velocity vector
u’: Turbulence intensity
uc: Local burning velocity
ud: Flame displacement speed
ūin: Mean inflow velocity
uL: Laminar burning velocity
uT: Turbulent burning velocity
V: Total volume of the computational domain
Y: Mass fraction
δf: Flame thickness
κ: Local flame stretch rate
λ: Taylor microscale
ρ: Density

Superscripts
0: Without flame stretch
Subscripts
a: In adiabatic condition
b: In burned product
u: In unburned mixture

























