Open Journal of Fluid Dynamics
Vol.05 No.02(2015), Article ID:56849,10 pages
10.4236/ojfd.2015.52015
The Large Scale Instability in Rotating Fluid with Small Scale Force
Michael Kopp1, Anatoly Tur2, Vladimir Yanovsky1
1National Academy of Science Ukraine, Institute for Single Crystals, Kharkiv University, Kharkov, Ukraine
2Institut de Recherche en Astrophysique et Planétologie, CNRS, Université de Toulouse [UPS], Toulouse, France
Email: anatoly.tour@irap.omp.eu
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 14 April 2015; accepted 30 May 2015; published 2 June 2015
ABSTRACT
In this paper, we find a new large scale instability in rotating flow forced turbulence. The turbulence is generated by a small scale external force at low Reynolds number. The theory is built on the rigorous asymptotic method of multi-scale development. The nonlinear equations for the instability are obtained at the third order of the perturbation theory. In this article, we explain the nonlinear stage of the instability and the generation vortex kinks.
Keywords:
Large Scale Vortex Instability, Coriolis Force, Multi-Scale Development, Small Scale Turbulence, Vortex Kinks

1. Introduction
It is well known, that the rotating effects play an important role in many practical and theoretical applications for fluid mechanics [1] and are especially important for geophysics and astrophysics [2] [3] when one has to deal with rotating objects such as Earth, Jupiter and Sun. Rotating fluids could generate different waves and vortex motions, for example, gyroscopic waves, Rossby waves, internal waves, located vortices and coherent vortex structures [4] -[7] . Among the vortex structures, the most interesting are the large scale ones, since they carry out the efficient transport of energy and impulse. The structures which have characteristic scale much more than the scale of turbulence or of the external force which generates this turbulence, are understood as large scale ones. At present, we can state that there are a lot of instabilities which generate the large scale vortex structures (see for example [8] -[14] ), in particular, in rotating fluid with the non-homogeneous turbulence [15] . In this work, we find the new large scale instability in rotating fluid, under impact of small external force which keeps up turbulent fluctuations. The nonlinear large scale helical vortex structures of Beltrami type or localized kinks with internal helical structure appear as a result of the development of this instability in rotating fluid. We can consider that external small scale force substitutes the action of small scale turbulence. It is supposed that external force is in plane (X, Y), which is perpendicular to the rotation axis, for example, axis Z is directed along the vector of angular velocity of rotation Ω. Helical 2D field of velocity Wx, Wy turns around axis Z, when Z changes in the kink which links the hyperbolic point and the stable focus (Figure 1). Moreover, this field does some turns in the kink, which links instable and stable focuses (Figure 2). The found instability belongs to the class of instabilities called hydrodynamic α-effect. For these instabilities, the positive feedback between velocity components of Wx, Wy is typical.
Figure 1. The kink which connects the hyperbolic point with stable knot with D = 1, C1 = 0.04, C2 = 0.04. When approaching the stable knot one can see rotations of velocity field.
Figure 2. The kink which connects the instable and stable focuses with D = 1, C1 = 0.04, C2 = 0.04. One can see the internal helical structure of the kink.

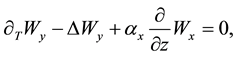
and leads to the instability. The α-effect is taking its origins from magnetic hydrodynamics, where it engenders the increase of large scale magnetic fields (see for example [16] ). It was generalized later for ordinary hydrodynamics. For the time being some examples of hydrodynamics α-effect [8] -[14] are already known. From this point of view, in this work we found a new example of α-effect. The theory of this instability is developed rigourously using the method of asymptotic multi-scale development, similar to what was done by Frisch, She and Sulem for the theory of the AKA effect [13] . This method allows finding the equations for large scale perturbations as secular equations of asymptotical theory in order to calculate the Reynolds stress tensor and to find the instability. The small parameter of asymptotical development is the Reynolds number R, . Our paper is organised as follows: in Section 2 we formulate the problem and the main equations in rotating system of coordinates; in Section 3 we examine the principal scheme of the multi-scale development and we give the secular equations. In Section 4 we calculate the velocity field of zero approximation. In Section 5 we describe the calculations of the Reynolds stress and find the large scale instability. In Section 6 we discuss the saturation of the instability and find non linear stationary vortex structures. The results obtained are discussed in the conclusions given in Section 7.
. Our paper is organised as follows: in Section 2 we formulate the problem and the main equations in rotating system of coordinates; in Section 3 we examine the principal scheme of the multi-scale development and we give the secular equations. In Section 4 we calculate the velocity field of zero approximation. In Section 5 we describe the calculations of the Reynolds stress and find the large scale instability. In Section 6 we discuss the saturation of the instability and find non linear stationary vortex structures. The results obtained are discussed in the conclusions given in Section 7.
2. The Main Equations and Formulation of the Problem
Let us examine the equations of motion for non-compressible rotating fluid with external force 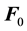 in rotating coordinates system:
in rotating coordinates system:
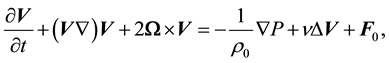 (1)
(1)
 (2)
(2)
The external force F0 is divergence-free. Here Ω-angular velocity of fluid rotation,  -viscosity,
-viscosity,  -con- stant fluid density. Let us design characteristic amplitude of force f0, and its characteristic space and time scale
-con- stant fluid density. Let us design characteristic amplitude of force f0, and its characteristic space and time scale  and
and 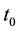 respectively.
respectively.
Then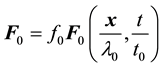 . We will design the characteristic amplitude of velocity, generated by external force as
. We will design the characteristic amplitude of velocity, generated by external force as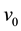 . We choose the dimensionless variables
. We choose the dimensionless variables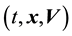 :
:
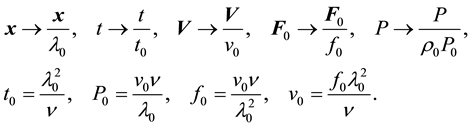
Then, in dimensionless variables the Equation (1) takes forme:




ber on scale











3. The Multi-Scale Asymptotic Development
Let us search for the solution to Equations (2) and (3) in the following form:



Let us introduce the following equalities: 




Using indicial notation, the system of equation can be written as



Substituting these expressions into the initial Equations (2) and (3) and then gathering together the terms of the same order, we obtain the equations of the multi-scale asymptotic development and write down the obtained equations up to order R3 inclusive. In the order R−3 there is only the equation

In order R−2 we have the equation

In order R−1 we get a system of equations:

The system of Equations (17) and (18) gives the secular terms

which corresponds to a geostrophic equilibrum equation.
In zero order R0, we have the following system of equations:

These equations give one secular equation:

Let us consider the equations of the first approximation R:


From this system of equations there follows the secular equations:


The secular Equations (27) and (29) are satisfied by choosing the following geometry for the velocity field (Beltrami field):

In the second order R2, we obtain the equations


It is easy to see that there are no secular terms in this order.
Let us come now to the most important order R3. In this order we obtain the equations

From this we get the main secular equation:

There is also an equation to find the pressure

4. The Velocity Field in Zero Approximation
It is clear that the most important is Equation (36). In order to obtain these equations in closed form, we need to calculate the Reynolds stresses


Let us introduce the operator

Using

Pressure 

Let us introduce designations for operatores:

and for velocities:



For simplicity, we choose the systeme of coordinates so that the axis Z coincides with the direction of angular velocity of rotation Ω. Then


It is obvious that divergence of this force us equal to zero. Thus, external force is given in plane (x, y), orthogonal to rotation axis.
The solution for equations system (34) can be found easily in accordance with Cramer’s Rule:

Here Δ is the determinant of the system (34):




After writing down the determinants in the explicit form, we obtain:




In order to calculate the expressions (40)-(43) we present the external force in complex form:

Then all operators in formulae (40)-(42) act from the left on their eigenfunctions. In particular:

To simplify the formulae, let us choose

We will designate

Before doing further calculations, we h ave to note that some components of tensors 


Taking into account the formulae (45)-(47), we can find the determinant:

In a similar way we find velocity field of zero approximation:



5. Reynolds Stress and Large Scale Instability
To close the Equations (27) we have to calculate the Reynolds stresses 

These terms are easily calculated with help of formulae (49)-(51). As a result we obtain:

Now Equations (27) are closed and take form:

We calculate the modules and write the Reynolds stresses (52) in the explicit form:

With small Wx, Wy Reynolds stresses (52) can be expanded in a series in the small parameters Wx, Wy. Taking into account the formula:
We obtain the linearized Equations (53):

We will search for the solution of linear system (55) in the form:

We substitute (56) in Equation (55) and obtain the dispersion equation:

The dispersion Equation (57) shows that equation system (55) has instable oscillatory solutions with oscillatory frequency 




6. Saturation of Instability and Nonlinear Vortex Structures
It is clear that with increasing of amplitude nonlinear terms decrease and instability becomes saturated. Consequently stationary nonlinear vortex structures are formed. To find these structures let us choose for Equations
(54) 

From Equations (58) follows:

After integrating the system of Equations (59) we obtain:

Integrals in expression (60) are calculated in elementary functions (see [17] ), which give the expression for first integral of motion J of Equations (59):
Equations (58) can be easily ca lculated numerically using standard tools. In particular, this allows to construct phase portrait of the dynamical system (58) (Figure 3) and to get the most interesting solutions which link singular points on phase plane. See for example Figure 1, where the hyperbolic singular point is connected with
Figure 3. Phase portrait of the dynamical system (58), with D = 1, C1 = −0.03, C2 = 0.03. One can see two hyperbolic singular points and stable and instable knots.
the stable knot and Figure 2, where the solution connects instable and stable focuses. All these solutions correspond to the large scale localized vortex structures of kink type with rotation, generated by the instability which has been found in this work.
7. Conclusions and Discussion of the Results
In this work we find the new large scale instability in rotating fluid. It is supposed that the small scale vortex external force in rotating coordinates system acts on fluid which maintains the small velocity field fluctuations (small scale turbulence with small Reynolds number R,
Let us note that unlike previous works about hydrodynamic α-effect in rotating fluid, the use of the asymptotic development allows constructing naturally the nonlinear theory and studying the stationary nonlinear vortex kinks.
References
- Grinspen, H.P. (1990) The Theory of Rotating Fluids. Breukelen Press, Brookline.
- Roberts, P.H. and Soward, A.M. (1978) Rotating Fluids in Geophysics. Academic Press, London.
- Clarke, C. and Carswell, B. (2007) Principles of Astrophysical Fluid Dynamics. Cambridge University Press, Cambridge. http://dx.doi.org/10.1017/CBO9780511813450
- Vallis, G.K. (2010) Atmospheric and Oceanic Fluid Dynamics. Cambridge University Press, Cambridge.
- Abramowicz, M.A., Lanza, A., Spigel, E.A. and Szuszkiewicz, E. (1992) Vortices on Accretion Disks. Nature, 356, 41-43. http://dx.doi.org/10.1038/356041a0
- Brandt, P.N., Scharmer, G.B., Ferguson, S., Shine, R.A., Tarbell, T.D. and Title, A.M. (1988) Vortex Flow in the Solar Photosphere. Nature, 335, 238. http://dx.doi.org/10.1038/335238a0
- Dritschel, G. and Legras, B. (1993) Modeling Oceanic and Atmospheric Vortices. Physics Today, 46, 44. http://dx.doi.org/10.1063/1.881375
- Moiseev, S.S., Sagdeev, R.Z., Tur, A.V., Khomenko, G.A. and Yanovsky, V.V. (1983) A Theory of Large-Scale Structure Origination in Hydrodynamic Turbulence. Soviet Physics―JETP, 58, 1149.
- Moiseev, S.S., Rutkevich, P.B., Tur, A.V. and Yanovsky, V.V. (1988) Vortex Dynamos in a Helical Turbulent Convection. Soviet Physics―JETP, 67, 294.
- Lupyan, E.A., Mazurov, A.A., Rutkevich, P.B. and Tur, A.V. (1992) Generation of Large-Scale Vortices through the Action of Spiral Turbulence of a Convective Nature. Soviet Physics―JETP, 75, 833.
- Khomenko, G.A., Moiseev, S.S. and Tur, A.V. (1991) The Hydrodynamic Alpha-Effect in a Compressible Fluid. Journal of Fluid Mechanics, 225, 355. http://dx.doi.org/10.1017/S0022112091002082
- Levina, G.V., Moiseev, S.S. and Rutkevich, P.B. (2000) Hydrodynamic Alpha-Effect in a Convective System. Advances in Fluid Mechanics, 25, 111.
- Frisch, U., She, Z.S. and Sulem, P.L. (1987) Large-Scale Flow Driven by the Anisotropic Kinetic Alpha Effect. Physica D, 28, 382. http://dx.doi.org/10.1016/0167-2789(87)90026-1
- Tur, A.V. and Yanovsky, V.V. (2013) Non Linear Vortex Structures in Stratified Fluid Driven by Small-Scale Helical Force. Open Journal of Fluid Dynamics, 3, 64. http://dx.doi.org/10.4236/ojfd.2013.32009
- Kitchatinov, L.L., Rudiger, G. and Khomenko, G. (1994) Large-Scale Vortices in Rotating Stratified Disks. Astronomy & Astrophysics, 287, 320.
- Moffat, H.K. (1978) Magnetic Field Generation in Electrically Conducting Fluids. Cambridge University Press, Cambridge.
- Gradshteyn, I.S. and Ryzhik, I.M. (2000) Table of Integrals, Series, and Prodacts. Academic Press, London.












