Open Journal of Fluid Dynamics
Vol.3 No.3(2013), Article ID:37041,13 pages DOI:10.4236/ojfd.2013.33022
Unsteady Cavitation Analysis Using Phase Averaging and Conditional Approaches in a 2D Venturi Flow
1LAMH, Université Laval, Quebec, Canada
2LEGI, UMR 5519, Grenoble, France
3LPO, UMR 6523, Brest, France
Email: stephane.barre@legi.grenoble-inp.fr
Copyright © 2013 Vincent Aeschlimann et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received June 5, 2013; revised July 4, 2013; accepted July 18, 2013
Keywords: Unsteady Cavitation; Sheet Cavity; Optical Probes; Venturi-Type Flow; Turbo Pump
ABSTRACT
The present study refers to a cavitating Venturi type section geometry characterized by a convergent angle of 18˚ and a divergent angle of about 8˚ where the sheet cavity presents typical self-oscillation behavior with quasi-periodic vapor clouds shedding. This work is an extension of previous works concerning void ratio measurements and velocity fields using double optical probe and constitutes a complete analysis of the two-phase structure of unsteady cavitating flow. This paper provides a new method based on conditional and phase averaging technique with wall pressure signal to treat experimental data in order to evaluate more precisely time-averaged and rms values of the void ratio and instantaneous velocity fields. Conditional analysis shows a different behavior of the two-phase flow dynamics leading to highlight high void ratio events linked to the break-off cycle. Unsteady phase averaging of the optical probe signal gives the evolution of the void ratio at each studied location in the venturi and shows that the fluctuations close to the wall (where the re-entrant jet is predominant) are in phase with the upper part of the cavity instead of the thickness of the cavity which is unchanged.
1. Introduction
In cryogenic rocket engines, an inducer stage is used to protect the main turbopump from cavitation. Because of the low pressure used in cryogenic fuels tanks, cavitation occurs at the inducer’s blade suction side. In this situation, cavitation has two main effects. At first, it affects the inducer performance and then the global pump performance. In a second step, it can induce several instabilities which may affect the global behavior of the entire engine fueling system (tanks, pipes, valves, pumps and combustion chamber).
A lot of experimental works (Kamijo et al. [1], De Bernardi et al. [2] and Hassan et al. [3] among others) have been performed on real inducers geometry in order to describe and classify all these cavitation instabilities. However, due to the excessive complexity of real inducer flows, it is difficult to develop a clever physical understanding of the physics of such cavitation instabilities from real inducers measurements. Then, in order to obtain a more accurate description of the cavitation sheets existing on the suction side of the inducer blade, a Venturi type geometry has been proposed. The main idea is to obtain a 2D flow which can be easily instrumented to perform more accurate diagnostics than in the real inducer geometry. It is decided to design this Venturi in such a way that the pressure field in these devices must be the same as the one existing over an inducer blade suction side (where the cavitation mainly develops). Two kinds of Venturi flows are then designed.
The first one which has a 4˚ divergent angle (Venturi 4˚) corresponds to the nominal operating point of the inducer. It features a quasi stable cavitation sheet. It has been extensively described in Stutz and Reboud [4], Stutz [5,6] and Barre et al. [7]. The main interest of these studies as compared to the one performed on real inducers relies in the fact that it permits the investigation of the cavitation sheet itself. It is then shown that the sheet, most of the time, is not composed of pure vapor. At the opposite, the majority of the sheet flow consists in a twophase mix between the vapor and the liquid phase. It has been also pointed out that it exists, even in stable cavity case such as the Venturi 4˚, a re-entrant jet in the rear part of the cavity. A lot of information concerning the void ratio distribution and some characteristics of the internal velocity field has been obtained in Venturi 4˚ flows thanks to these efforts [7].
The main consequence of these results was a great change in the physical perception of such flows which were only considered in the past as pure vapor sheets with almost no internal dynamics and no interaction with the external flow. This new approach leads to subsequent progress in numerical simulations of such flow configuration making possible a global homogeneous modelisation in RANS code (Coutier et al. [8], Reboud et al. [9], Goncalves et al. [10-12] and Decaix et al. [13]) compared to the very simplified approach used in the past.
The second Venturi flow developed was the Venturi 8˚. It corresponds to a partial flow-rate operating point for the inducer. In this case, the flow incidence on the inducer blades is quite high leading to a partial stall of these blades. In this situation, the cavitation sheet mainly consists in a detached vortical zone in which a two-phase fluid is embedded and convected downstream in a very unsteady manner. It was pointed out that this unsteadiness maybe responsible for the observed cavitation instabilities on real inducers geometry. Then, these flow configurations, and particularly, these unsteadiness characteristics, were extensively studied [14,15]. It was found that the cavity dynamics was quasi-periodic and that the void ratio values were quite low and never exceeded 25% for unsteady situations. Nevertheless, the unsteady behavior of the sheet cavity leads a major difficulty for simulations taking into account the interplay between cavitation and turbulence regarding the unsteadiness and the specific break-off cycle of the vapor phase. Indeed, the time averaged velocity profiles showed discrepancies in the cavity closure region due to the RANS approach where the turbulence-cavitation interactions were not fully taken into account. To get the unsteady behavior of quasi-peridodic cavitating structures, Large Eddy Simulations may be used to simulate the sheet/cloud cavitation phenomena. In this way, Dittakavi et al. [16] performed a LES of cavitation in a venturi nozzle in order to capture at the venture throat the specific irregular shedding of small scale vapor structures near the turbulent cavity closure region. They showed that these structures were responsible of vorticty production resulting in the formation of hair-pin vortices. De Lange et al. [17] observed that the re-entrant jet had a spanwise component which resulted in the formation of hair-pin vortices. This is the reason why it is obvious to get more insight about the physical mechanism of the shedding process using new experimental data-processing based on unsteadiness study. The main topic of this paper is to give a new insight about unsteady cavitation process in the venturi 8˚ flow type. The idea is to join phase averaging techniques and conditional measurements of the void ratio and vapor phase velocity in the sheet cavity. This technique allows a refined analysis of the cyclic phenomenon. Phase averaging process is performed using wall pressure signal as time reference.
The experimental facilities and operating conditions are presented in Section 2. The measuring techniques— dual fiber-optic probe for the dynamic characterization of the vapor phase are also described. An overview of experimental results concerning void ratio and vapor phase velocity is given in Sections 3 and 4.
2. Experimental Set-Up and Measurements
2.1. Experimental Set-Up
Experiments have been performed in a closed loop at CREMHyg lab in Grenoble and the test section is 520 mm long, 44 mm wide and 50 mm high in the inlet. The tested flow configuration corresponds to flat upper and side walls, whereas the height of the lower wall varied in order to form a convergent-divergent nozzle. In the present considered experiments, “venturi 8˚”, the convergent part of the lower wall (between inlet and throat) exhibits a 18˚ angle and the maximum angle of the divergent part was 8˚. The inlet pressure Pinlet can be tuned and was lowered until the desired cavitation number allowing a specific unsteady behavior of the sheet cavity is obtained. The cavitation number at the inlet section was defined as:
 (1)
(1)
where Pvap was the vapor pressure and Pinlet, Vinlet, were the pressure and velocity respectively at the reference section upstream of the venturi.
The divergent part was equipped with eight probe holes to take various measurements such as the instantaneous pressure, local void ratio and velocity in the sheet cavity. Specific probe locations are presented in Figure 1 for the tested case.
By fine tuning both the velocity and the pressure (Vinlet and Pinlet) it was possible to obtain several sheet cavity behaviors. The present choice leads us to tune the flow in order to obtain a sufficiently large and unstable sheet but
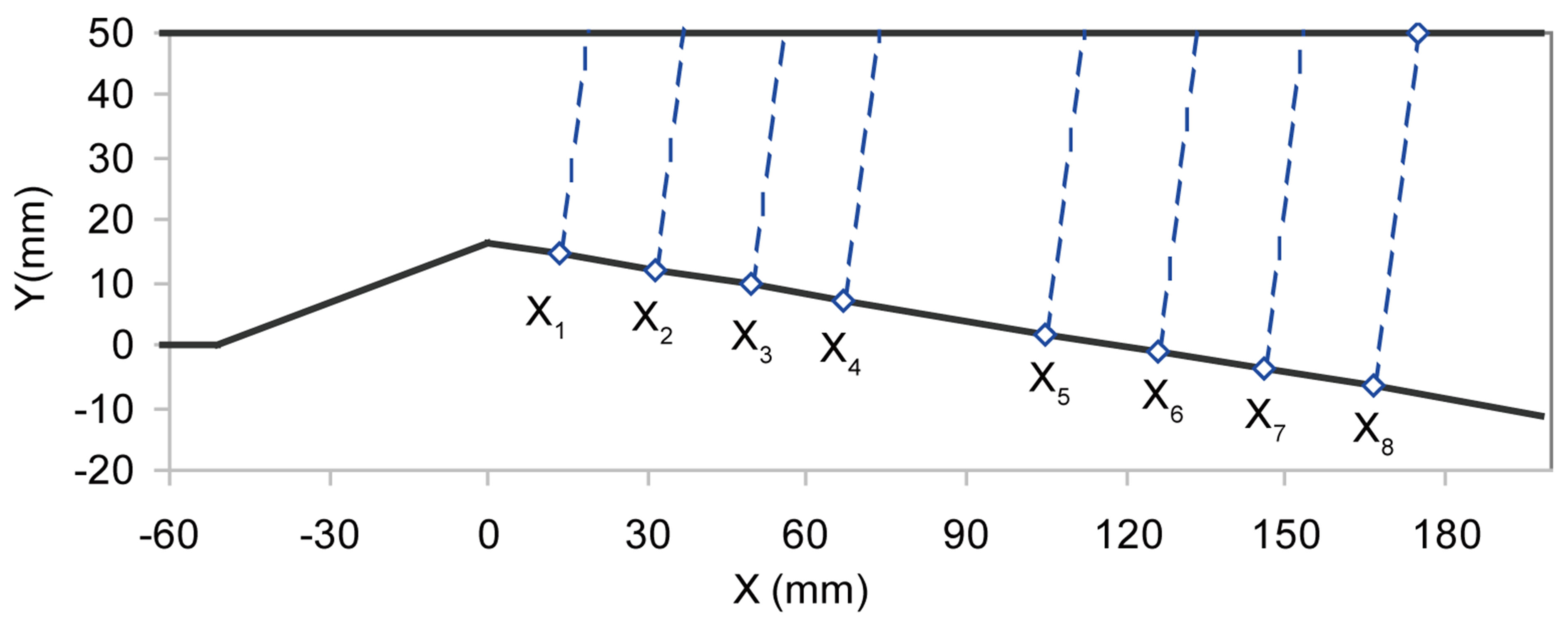
Figure 1. Venturi design and probe locations. X1 = 13.7 mm; X2 = 31.5 mm; X3 = 49.9 mm; X4 = 67.7 mm; X5 = 106 mm; X6 = 126.9 mm; X7 = 147.1 mm; X8 = 168.3 mm.
without very huge break-off cycles which may lead to unmanageable global flow-rate fluctuations of the entire testing loop. An operating point was then chosen to match all the previous constraints. Concerning the geometrical data, Lref = 224 mm is the reference length and corresponds to the distance between the inlet section and the last probed station (X8). The Reynolds number Re = 3.1 × 105 is based on Vinlet and on the test section width (44 mm). Xref is the averaged cavity length (45 mm).
With these previous parameters and according to experimental observations, cavitation sheets developed from the venturi throat. A typical self-oscillation behavior was observed with quasi-periodic vapor clouds shedding and the mean attached cavity length value was 45 ± 5 mm (»0.2 Lref). Some instantaneous pictures of the cloud shedding are presented in Figure 2.
The stream goes from right to left and the throat is located on the right side of the pictures. At the first step (Figure 2(a)) an attached cavity is observed at the throat and slightly downstream a horseshoe shaped detached cloud is observed. At the second step (Figure 2(b)), the sheet reaches its maximum length and the cavity breaks in two parts at the third step (Figure 2(c)). The detachment of the vapor phase is due to the onset of reverse flow between the cavity and the venturi wall. This reverse flow is called “re-entrant jet”. At the fourth step, the downstream part is swept along within the stream and starts to collapse while the attached part starts another cycle (Figure 2(d)). This particular behavior has been observed within various experimental studies (De lange et al. [17] and Foeth et al. [18] and). In the present case the corresponding frequency is close to 45 Hz (which corresponds roughly to »1.4Vref/Lref) leading to a classical Strouhal number of about 0.3 when based on the cavity length.
2.2. Measurements
2.2.1. Pressure Measurements
Pressure measurements were carried out using a piezoelectric sensor DRUCK model PMP4070, with a maximum range of 70000 Pa and absolute precision of ±19 Pa
 (a)
(a) (b)
(b) (c)
(c) (d)
(d)
Figure 2. Instantaneous pictures of a break off cycle. (Flow is from right to left).
and the relative precision is ±0.027%. The mean and fluctuating values of the wall pressure have been measured upstream to characterize the cavitation number and at any stations in the divergent area especially inside the vapor cavity and in its wake. In order to perform a phase averaging of the data, the pressure signal was recorded at station 5 simultaneously with the optical probe one; this signal, being periodic, was then used as a time reference for the phase averaging process. Pressure signal was recorded at a sampling rate of 50 kHz. 6 millions of samples were taken for each measurements leading to an observation time of 120 s which is sufficient to perform the mean and root mean square (rms) value computation. The cavitation number was sinlet = 1.998% ± 0.11%, where Pinlet = 0.517% ± 0.03% and Vinlet = 7 m/s, at the reference section upstream of the venturi and it was verified that the mean and the most probable values are almost even. Figures 3(a) and (b) show the longitudinal evolution of the mean and normalized rms value of the wall pressure along the venturi. The mean pressure is here presented via the ratio:
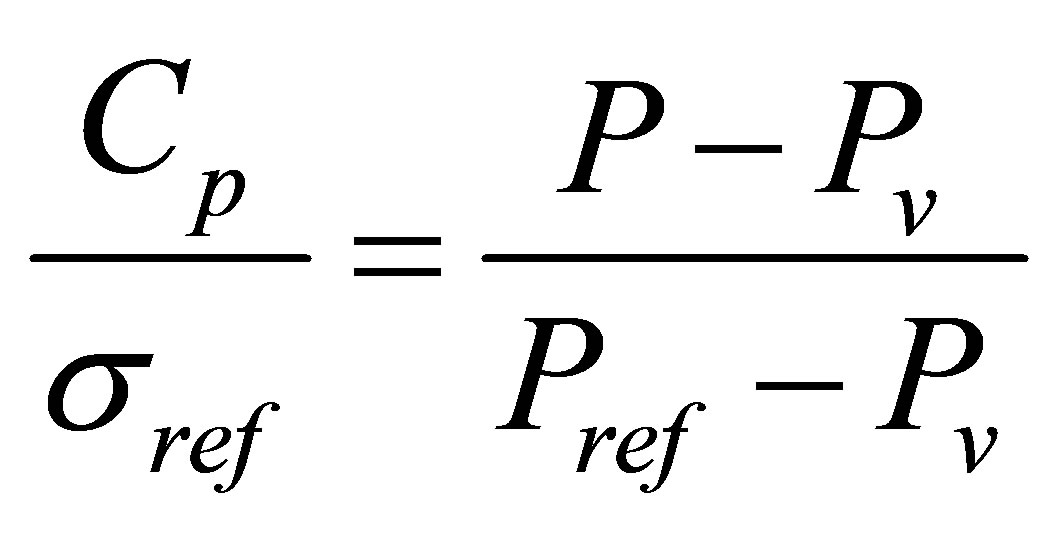 (2)
(2)
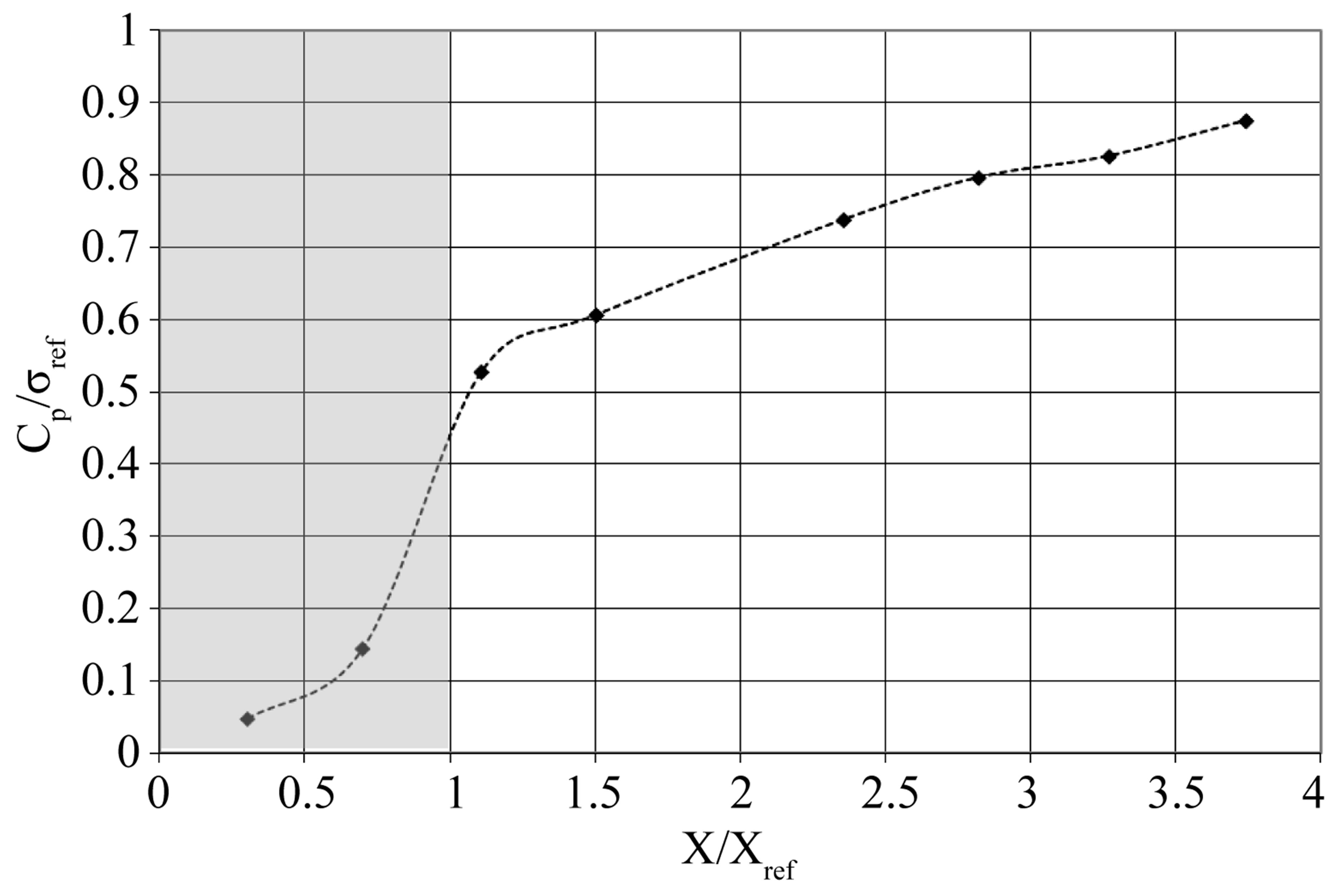
where P is the measured mean pressure value. The mean observed sheet length (Xref » 45 mm) is also represented (gray area) and the longitudinal coordinate X is normalized to Xref. The mean pressure increases continuously when going downstream. The positive pressure gradient is maximum at the sheet rear end near X/Xref » 1 corresponding to the cavity closure zone. Downstream, a quasi linear monotonic pressure increase due to the venturi geometry is observed. It is easily shown that, almost in the probed range, the mean wall pressure never reach the vapor pressure value (Pv). However, the flow is diphasic and vapor is created even if the mean pressure remains superior to Pv in almost all the sheet zone. In fact, vapor is created due to the unsteady and turbulent nature of the flow in which turbulent eddies generate unsteady low pressure zone where the vapor creation process may take place and then, this vapor is transported by those eddies in the break-off cycle process.
The maximum level of the rms value (Figure 3(b)) is reached at the first probed position with a value of PRMS/Pmean close to 20%. Further downstream, this level start to decrease quite sharply to reach an almost null value downstream of the sheet rear end (near X/Xref » 1.5). A “remanent” level of about 5% is obtained near X/Xref » 2.3 which may corresponds to some complex interaction between the shedding process and the wall itself. However it seems clear that the initial detachment process occurring upstream of the sheet leads to large pressure fluctuations which seems to be damped when going downstream.
 (a)
(a) (b)
(b)
Figure 3. (a) Longitudinal evolution of the mean wall pressure across the flow; (b) Longitudinal evolution of the normalized RMS pressure fluctuations.
2.2.2. Two Phase Flow Measurements
For the two-phase flow measurements, double optical probe was used to evaluate void ratio and velocity fields. It was constituted by two sapphire optical fibers (see Barre et al. [7] for technical details about the probe). Due to the low void ratio in this flow configuration refined data acquisitions have been carried out in order to obtain sufficiently converged statistics and to perform an unsteady phase averaging analysis of the data. The most important difference with respect to previous work15 concerns the geometry of the double optical probes and the data processing. Indeed, in the present study, we used an optical probe made of two sapphire optical fibers of 80 mm diameter and with frayed ends. The inter-tips distance is 1.05 mm ± 0.02. In previous work, the inter-tips distance was about 2 mm. The optical probe previously used was constituted of two glass fibers with a 50 mm tip diameter. This characteristic caused a lot of breaking probe problems due to the aggressiveness of the studied unsteady flow. The data acquisitions were carried out on a fast A/D data acquisition board NI-DAQ PCI-6110E. For each acquisition we recorded 4 million points per way (one way per optical probe), with a sampling rate of 100 kHz (giving 40 seconds of acquisition per measurement). For each Y position of the double optical probe in the venturi, the process was repeated 100 times in order to generate 400 million data per position in the cavity corresponding to an observation time of 4000 s per Y position which can be compared to 0.45 million data (6 s of acquisition) per probe position recorded and treated in previous study [15].
3. Processing Technique for Void Ratio and Vapor Phase Velocity
3.1. Estimation of the Local Void Ratio
The local void ratio a of a gas/liquid mixture is defined as the ratio between the cumulated time of gas phase at the tip of the probe (Tvap_i) and a given time of observation. It is given by:
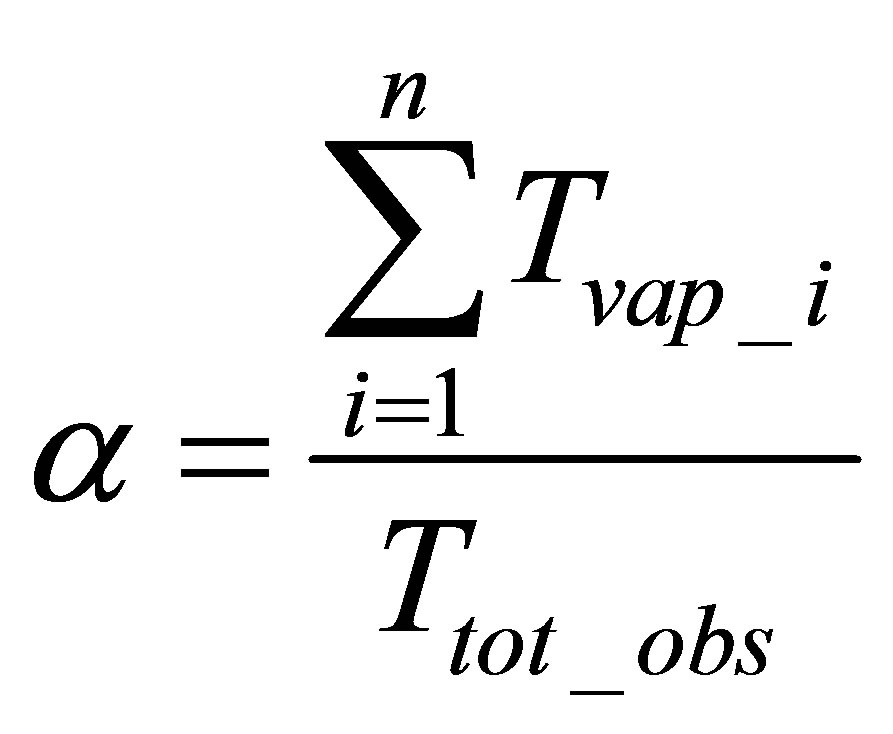 (3)
(3)
Figure 4 shows an idealized optical probe signal, the maximum value Vmax corresponds to the vapor state, and the minimal value Vmin to the liquid state. The used post-processing algorithm enables us to exploit the signal from the optical probe, by distinguishing the gas phase from the liquid phase according to the value of the measured tension. In order to estimate the local void ratio, a threshold in tension Vthreshold was chosen carefully and it allows us to determine the phase of the fluid around the probe: liquid state if V < Vthreshold and gas state if V > Vthreshold. This threshold was fixed according to the parameter:
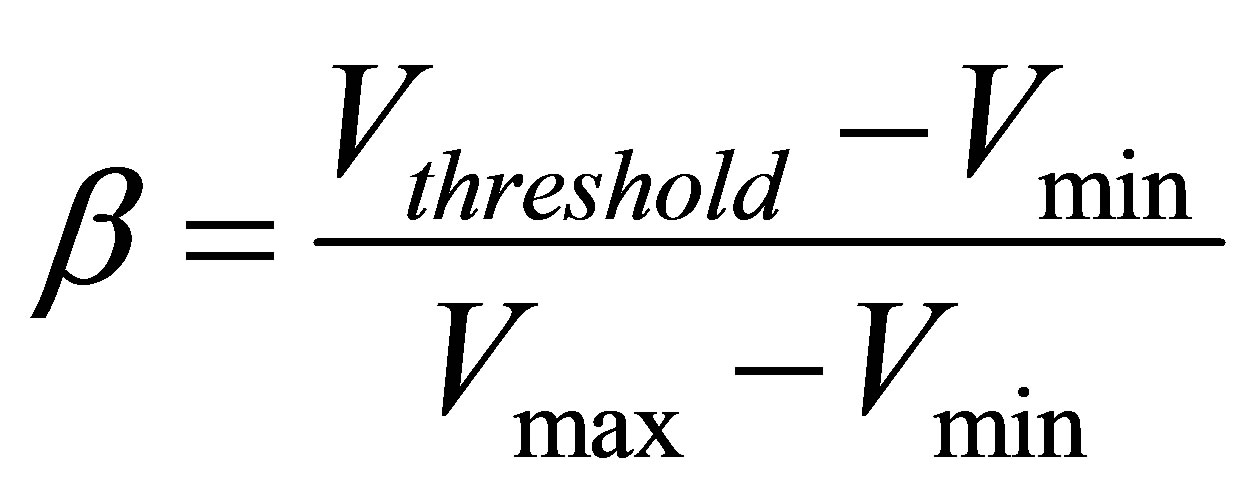 (4)
(4)
The value of this parameter was gauged in great detail for this type of flow [4-6,15]. They retained a value of b = 0.1 to give correct void ratios for this typical flow pattern. We used this value for the determination of the void ratio. For more details about the void ratio determination, see Barre et al. [7].
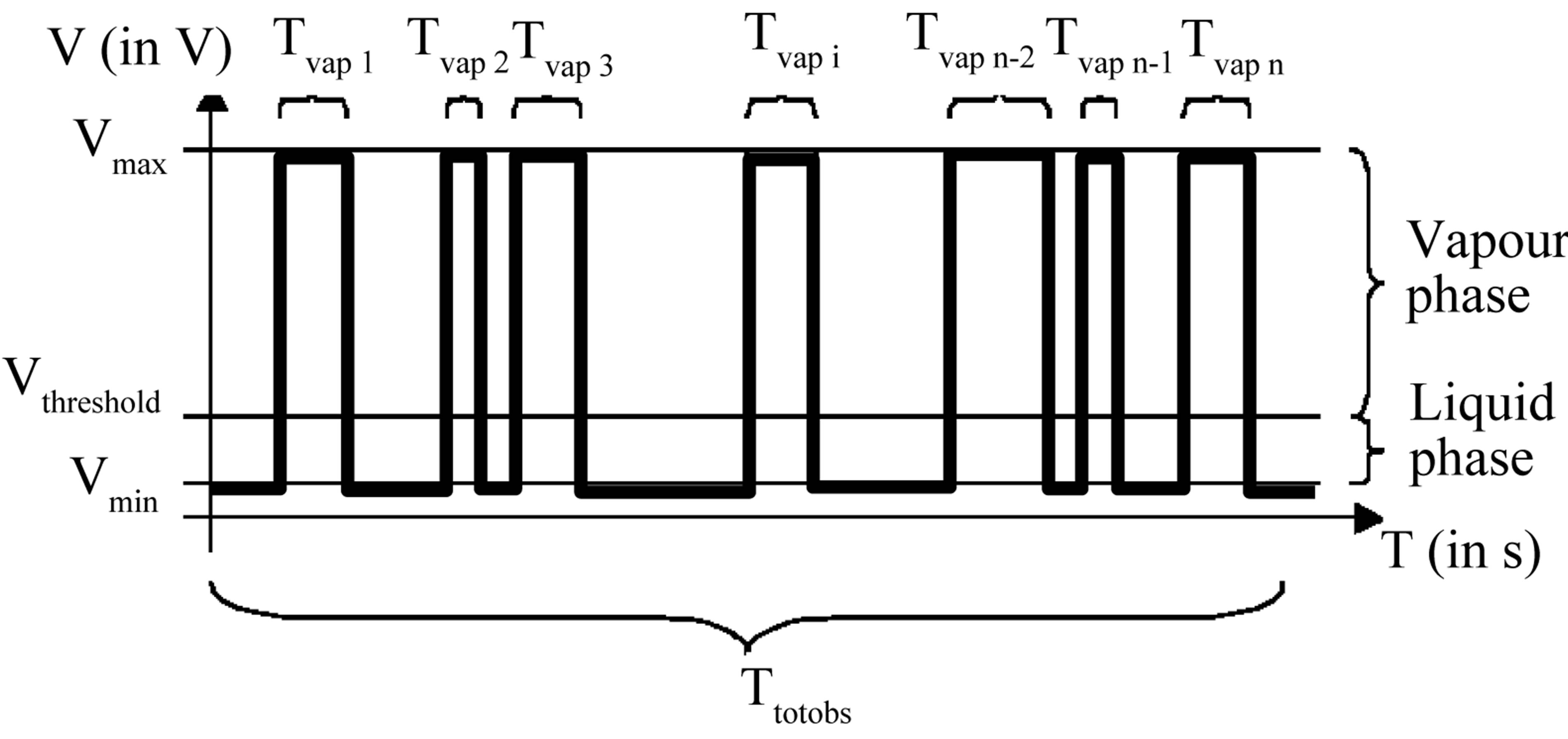
Figure 4. Schematic probe signal—Phase detection.
3.2. Estimation of the Instantaneous Local Velocity
The determination of the local velocity was based on the method detailed in Barre et al. [7]. The used double optical probe, aligned in the direction of the flow, produces two distinct signals (S1 upstream and S2 downstream). Those electric signals are thus analyzed and broken up by introducing two tension thresholds as shown in Figure 5. The low threshold Vlow, taken on the rising part of the electric signal, leads us to detect the beginning of the crossing of a vapor bubble. The high threshold Vhigh is considered to detect the end of the crossing of the bubble on the downward part of the signal (see Figure 5). A bubble is taken into account in the analysis only when these two thresholds are crossed consecutively.
The values of the low and high thresholds are defined from the imposed values of blow and bhigh with:
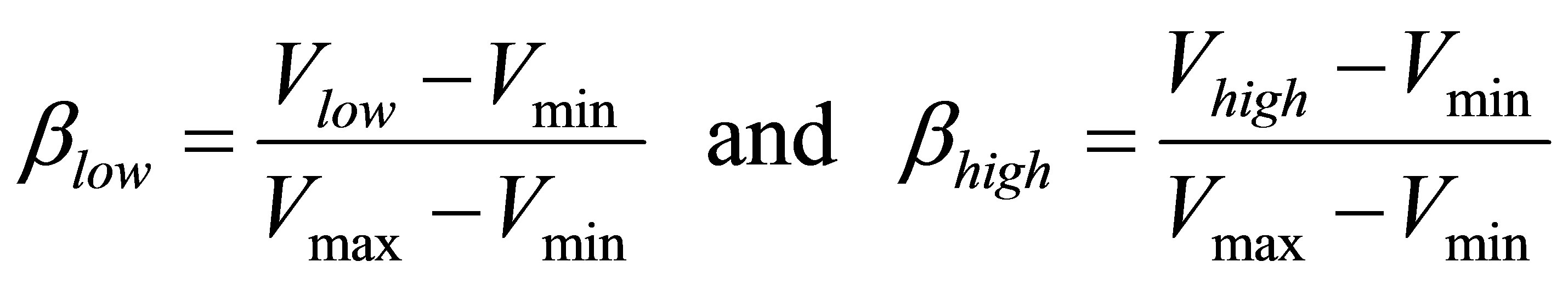 (5)
(5)
In the present study we used the value of blow = 0.2 proposed by Stutz et al. [4-6,14,15].
Concerning bhigh, its value has been reduced to 0.54 instead of 0.8 used by the same authors in order to obtain a substantial increase of the detected bubbles population. Some validations were carried out and confirm that this data rate increase is obtained without any degradation of the quality of the velocity field determination.
From these measurements, it was possible to deduce the tangential component (parallel to the profile) of the instantaneous local velocity by considering the temporal shift between the two traces provided by a bubble crossing successively the two tips of the probe. This optimal shift, called interval Itauopt, was recorded and corresponded to the number of sampling data between the considered traces as shown in Figure 6.
Then Itauopt is converted into a time interval using Tech, the sampling period (Tech = 10−5 s)
 (6)
(6)
The velocity is then deduced by:
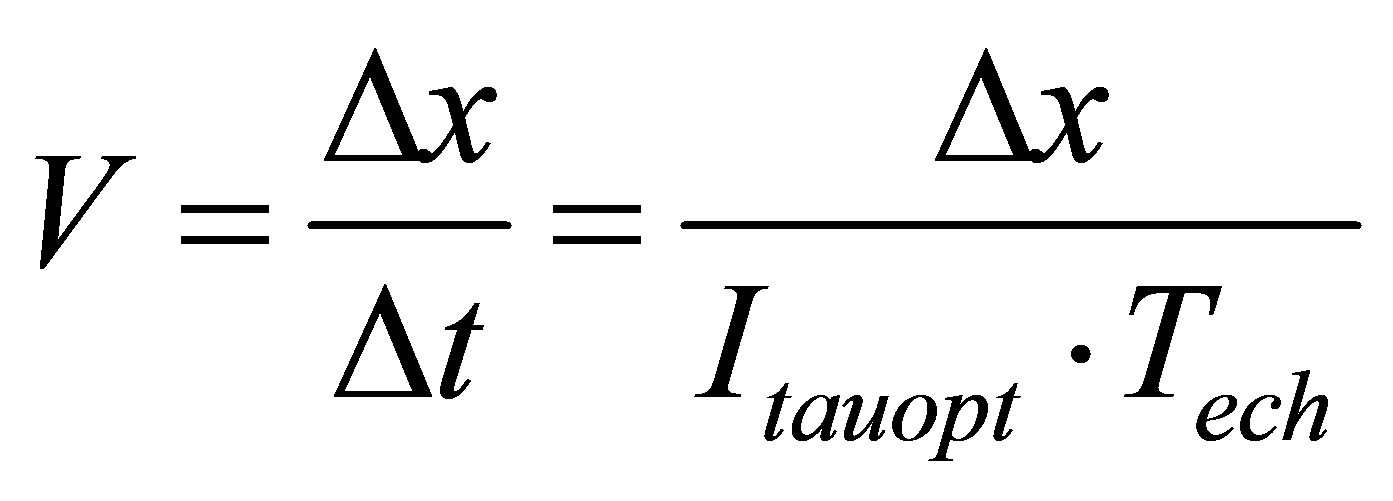 (7)
(7)
where Dx is the distance between the two probe tips (Dx = 1.05 mm).
This method which aims to obtain instantaneous velocities values was based on the determination of the convective velocity of some selected bubbles being respectively detected by the two probes. As a matter of fact, the velocity calculation algorithm rejects a lot of bubbles and then only about 10% of the detected bubbles are validated to give a useable velocity value.

Figure 5. Bubble localization using threshold method.

Figure 6. Itauopt definition.
4. Unsteady Void Ratio and Velocity Fields Description with Phase Averaging and Conditional Analysis
As described in Stutz et al. [14], the periodic fluctuations of the cavity can be characterized by a “break off cycle” where the length of the cavity grows with a mean velocity of 0.4 Vref, then the cavity is divided in two, the first part stays attached to the throat and a vapor cloud is convected downstream and collapses. In order to characterize a typical vapor cloud shedding, the choice of computing a phase averaged vapor shedding by dividing the period into five parts has been made. The pressure signal recorded downstream (at position X4 = 67.7 mm) is used as time reference because of its quasi-periodicity at 45 Hz like the “break-off cycle”. The phase averaging algorithm does not use a constant value for the pulsating period but determines, for each pulsation of the flow, the corresponding period. With this precaution, phase averaging can be done even in the present situation where the flow pulsation frequency is not perfectly constant but depends on the considered period. The main objective was then to compare the void ratio and velocity field distribution between the conditional and phase averaged methods and classical method in order to highlight the difficulties relative to the measurements of the unsteady behavior of the vapor phase. In this section, results concerning the void ratio are presented firstly followed by the velocity distributions and discussion about the physical mechanism of the break-off cycle.
4.1. Void Ratio
To describe the void ratio field dynamics, unsteady phase averaging has been performed and the evolution of the mean and standard deviation of the void ratio during a typical (phase-averaged) break-off cycle are presented on Figures 7 and 8 for each probed station. The typical period has been divided in 5 parts, each step corresponds to roughly 4.4 ms and then a phase averaging process has been performed. This phase averaging process consists, for each break-off cycle, in cutting the pressure signal in five equal parts. After that, for each time part of the cycle,

Figure 7. Phase averaged void ratio. (a) station 1; (b) station 2 and (c) station 3.

Figure 8. Standard deviation of the void ratio.
corresponding bubbles are detected on the optical probe signal. Then, these bubbles are processed in order to calculate their void ratio and a phase-averaged mean voidrate.
The standard deviation was defined as follow:
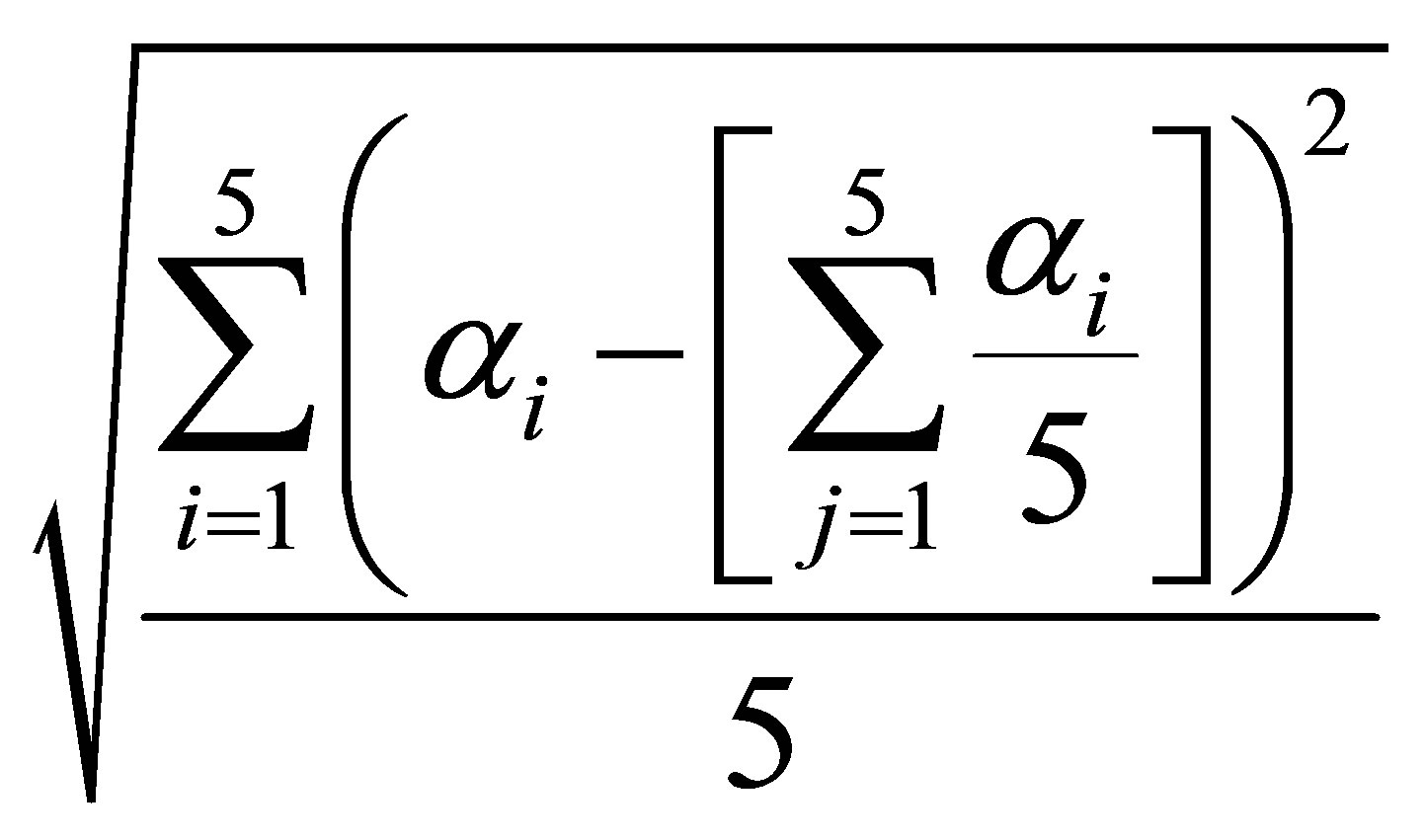 (8)
(8)
The mean phase averaged void ratio distribution inside the cavity is presented in Figure 7 for each probed station; X1 = 13.7 mm; X2 = 31.5 mm and X3 = 49.9 mm versus the transversal position. The transversal and longitudinal coordinate are reduced using respectively the local cavitating sheet thickness (Yref,i) and the mean sheet length Xref. Here Yref i are the cavity thicknesses for the considered stations: Yref 1 = 3.5 mm; Yref 2 = 8 mm; Yref 3 = 12.5 mm and Xref is the mean attached cavity length which is about 45 mm. The method for the estimation of the local sheet thickness was based on the zone determination where the void ratio was greater than 0% in the context of the spatial resolution of the void ratio measurement (0.5 mm) [7]. The classical mean values of the void ratio are superimposed to the phase averaged ones.
For stations 1 and 3, the mean phase averaged void ratio spatially oscillates in-phase and it can be seen a maximum peak value at the fifth step and a minimum value between the second and the third one. The evolution of void ratio in a given section is either growing or reducing. The fluctuations of the void ratio close to the wall (at the re-entrant jet region) and in the upper part of the cavity, are in-phase. The thickness of the cavity at each station does not change during a “break-off cycle”. We notice that, at station 2, fluctuations are low and the void ratio profile is quite steady. The station 3 is located just after the extremity of the attached part of the cavity where vapor cloud breaks away. It is important to note that the void ratio is never null over the whole section at any step. There are always few bubbles of vapor even between two clouds of vapor.
Figure 8 shows the normalized RMS evolution of the void ratio for each plotted station. Maximum relative fluctuations are obtained at station 3 because of the very low mean void ratio value inducing a strong effect on the RMS value for almost all the travelling bubbles localized in this flow region. At station No.1 the spatial repartition of the void ratio RMS fluctuations is not homogeneous and it exhibits a maximum value located near the sheet half height. This place may correspond to the maximum vapor generation area. At the opposite, for station No.2, it can be observed a very low and homogeneous fluctuation level. It then can be concluded that an almost steady situation is experienced at this station.
In order to provide a better visualization of the phase averaged fluctuations dynamics, the spatially integrated dimensionless value α* (centered and normalized) of the phase averaged void ratio has been computed using the formula:
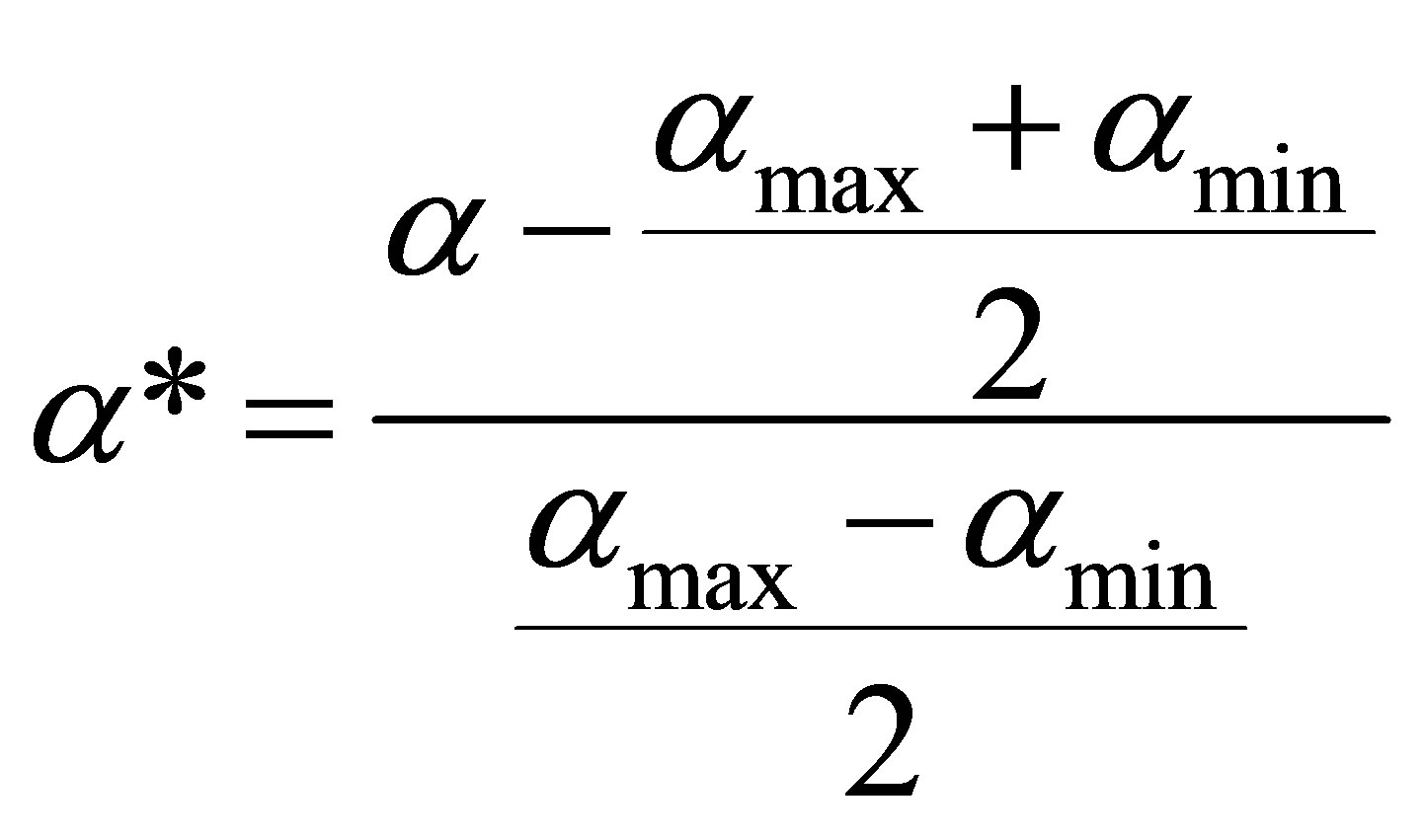 (9)
(9)
with
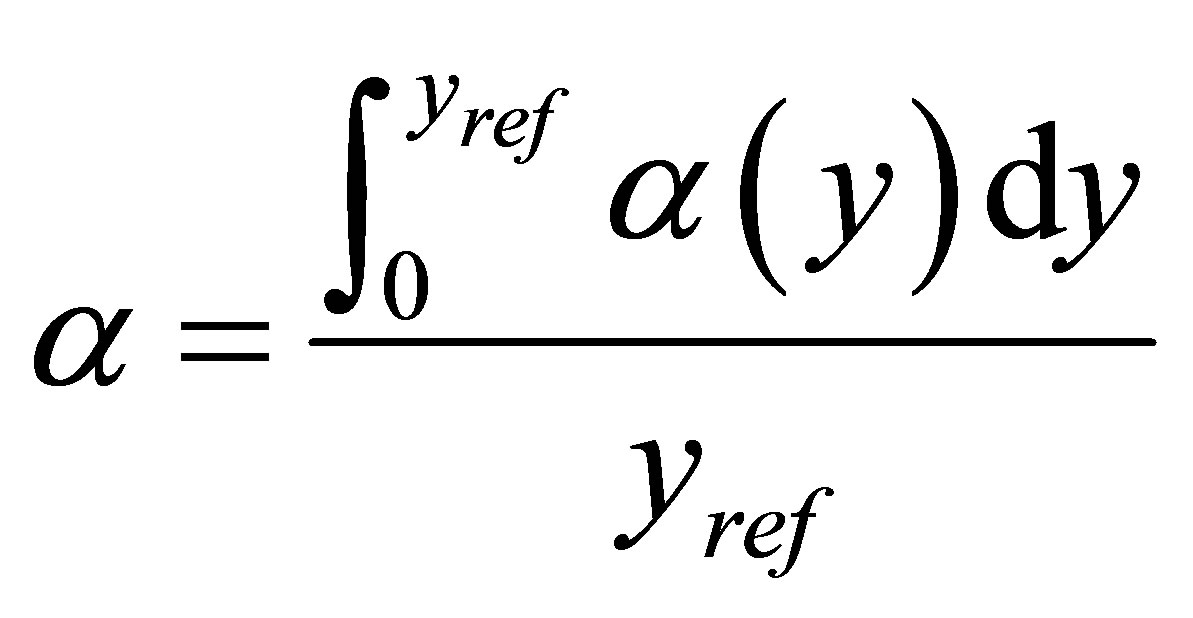 (10)
(10)
In which a is the space and phase averaged void ratio and  and
and ![]() are the spaced and phase averaged void ratio at the steps where there is respectively the maximum and the minimum amount of vapor (as an example, at station 1 and 3, the space and phase averaged void ratio is maximum at the 5th step, this is where
are the spaced and phase averaged void ratio at the steps where there is respectively the maximum and the minimum amount of vapor (as an example, at station 1 and 3, the space and phase averaged void ratio is maximum at the 5th step, this is where  is defined). Figure 9 presents the space and phase averaged void ratio evolution for each step during the breakoff cycle. For clarity purpose, this evolution is plotted over three periods.
is defined). Figure 9 presents the space and phase averaged void ratio evolution for each step during the breakoff cycle. For clarity purpose, this evolution is plotted over three periods.
It can be observed that whatever the station, the void ratio evolution is pulsated corresponding to the break-off cycle. To illustrate the relative intensity of such fluctuations in a typical cycle we compute the ratio between their root mean square and mean values over a phase averaged period. Figure 10 displays this longitudinal evolution versus X/Xref. The maximum relative void ratio fluctuations are obtained at station X3 where, at the same time, the mean void ratio value is the lowest. This illustrates the fact that the cavitation sheet closure zone is highly unsteady leading to large relative void ratio fluctuations of up to 30% of the mean value. This behavior is opposed to the one observed for the pressure fluctuations

Figure 9. Spatially and phase averaged void ratio evolution over 3 periods.
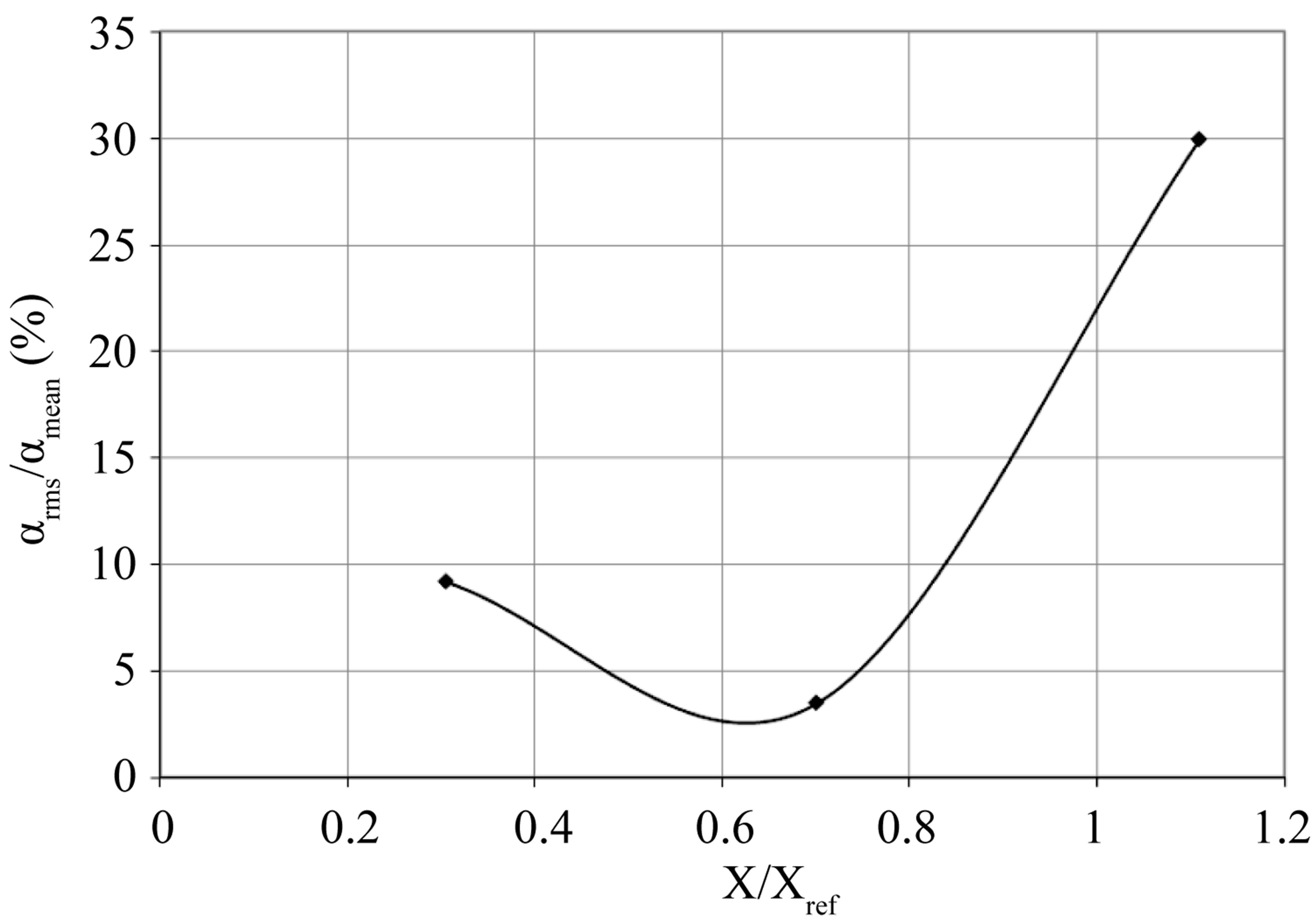
Figure 10. Normalized void ratio fluctuations over a breakoff cycle.
(see Figure 3(b)) where the maximum relative fluctuation level is obtained at X1 and then decreases sharply when going downstream. This experimental evidence may lead to some important consequence in term of cavitation modeling. It shows that a classical barotropic approach used in some cavitating flow numerical simulations (Fortes Patella et al. [19]) in which the pressure and the void ratio are linked by a direct functional dependence may not be able to reproduce the present experimental results.
4.2. Velocity Fields
In this section we firstly present the probability density function (PDF) of the velocity for each station at different vertical position in the sheet cavity. Specific transversal locations have been chosen for each station in order to take into account the longitudinal evolution of the thickness of the cavity: close to the wall, in the middle of the sheet cavity and in the cavity upper boundary. PDF are plotted on Figures 11(a), (b) and (c) and exhibit an oscillating shape between positive and negative value of the velocity except at station 3 where the velocity is mainly positive.
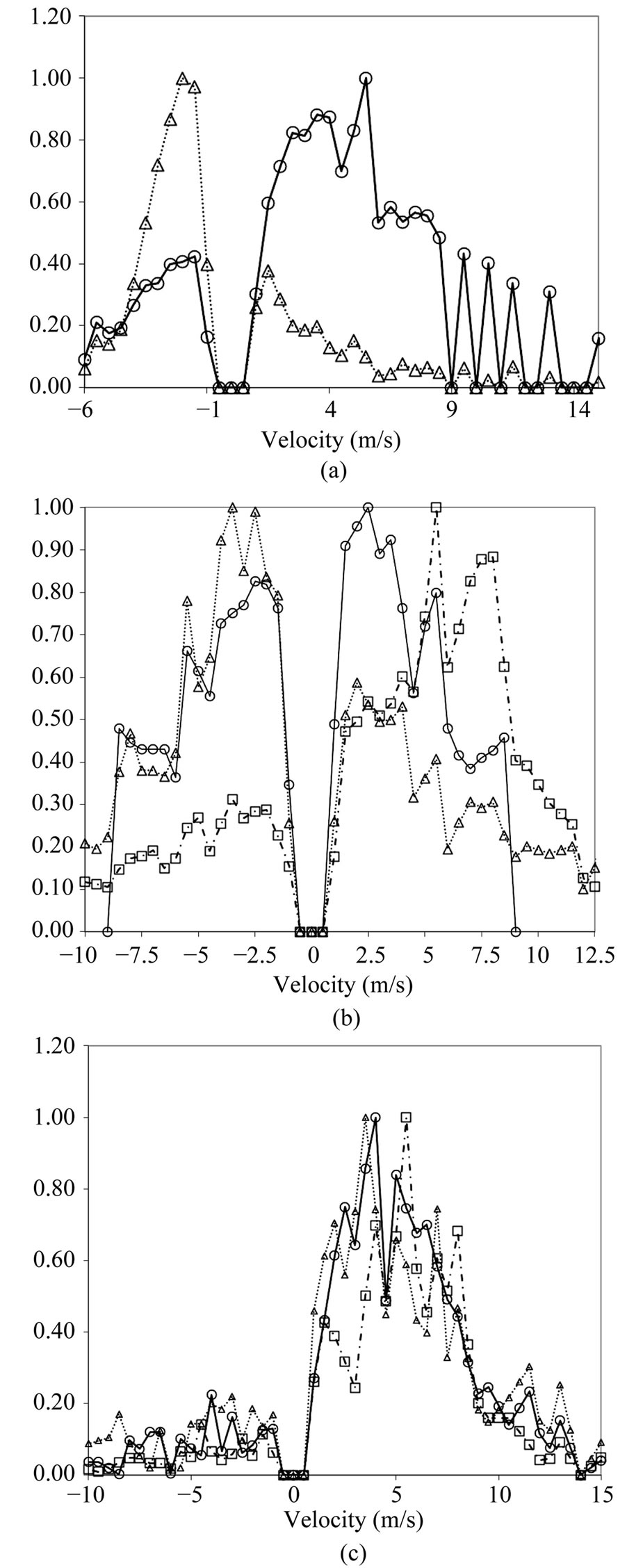
Figure 11. (a) Velocity PDF at station 1: r: Y/Yref1 = 0.28, Vmean = −1.3 m/s and Vmost-probable = −2 m/s; ™: Y/Yref1 = 0.86, Vmean = 2.72 m/s and Vmost-probable = 5.5 m/s; (b) Velocity PDF at station 2: r: Y/Yref2 = 0.125, Vmean = −1.25 m/s and Vmost-probable = −3.5 m/s; ™: Y/Yref2 = 0.375, Vmean = −0.49 m/s and Vmost-probable = 2.5 m/s; £: Y/Yref2 = 0.75, Vmean = 2.65 m/s and Vmost-probable = 5.5 m/s; (c) Velocity PDF at station 3: r: Y/Yref3 = 0.16, Vmean = 3.38 m/s and Vmost-probable = 3.5 m/s; ™: Y/Yref3 = 0.32, Vmean = 3.9 m/s and Vmost-probable = 4 m/s; £: Y/Yref3 = 0.64, Vmean = 4.5 m/s and Vmost-probable = 5.5 m/s.
At station 2 for example, when the location measurement is just up to the border of the re-entrant jet (Y/Yref2 = 0.375), it can be observed two main peaks with similar occurrences with respective most probable values of about −2.5 m/s and 2.5 m/s. In this region, the mean velocity only represents the average of those two values pondered by their probabilities of occurrence. The boundary of the re-entrant jet may then be defined by the location where occurrences of these peaks are equal. For stations 1 and 2, close to the wall, the peak with negative velocities values outweighs the one corresponding to positive ones. This behavior is characteristic of the reentrant jet. Getting away from the wall, the negative peak disappears and the positive one increases. The two peaks are even at the re-entrant jet border and then the positive peak outweighs the negative one where the fluid goes downstream. Station 3 is located in the region corresponding to the cavity closure and the velocity is always positive. As shown in the previous figures, the obtained velocity probability distributions are not Gaussian, so the mean velocity is not representative of the dynamic behavior of the fluid. This fact constitutes the main characteristic of this unsteady velocity field. From these data, we will be able to describe the velocity field inside the cavity.
Taking into account the previous results let us now consider the transversal evolutions of the longitudinal velocity for the three considered measurement stations. A particular attention is paid on the comparison between the classical mean values and the most probable values. Figure 12 exhibits the transversal evolution of both the classical mean velocity value and the most probable one. This representation is completed with the phase averaged values of the velocity obtained for both the five studied shedding cycle steps. In order to better describe the internal cavity dynamics, a phase averaging analysis has been performed on the velocity field. The data were obtained by cutting each signal period in five parts as was previously done for the void ratio. With this decomposition we can describe the typical cavity break-off cycle. Results are presented on the same figures which show the velocity profiles inside the cavity for the five steps observed during the break off cycle.
From a qualitative point of view, it can be seen for station 1 and 2 that a recirculating flow is present. It corresponds to the re-entrant jet associated with the negative velocity values shown on Figure 12. At station 3, the mean and most probable values exhibit a classical near wall turbulent boundary layer velocity profile. By comparisons, the mean value approach underestimates the extent and the intensity of the re-entrant jet, especially at station 2 where the unsteadiness is more pronounced.
Furthermore, we can observe that the velocity at the upper border of the cavity does not fluctuate in the con-
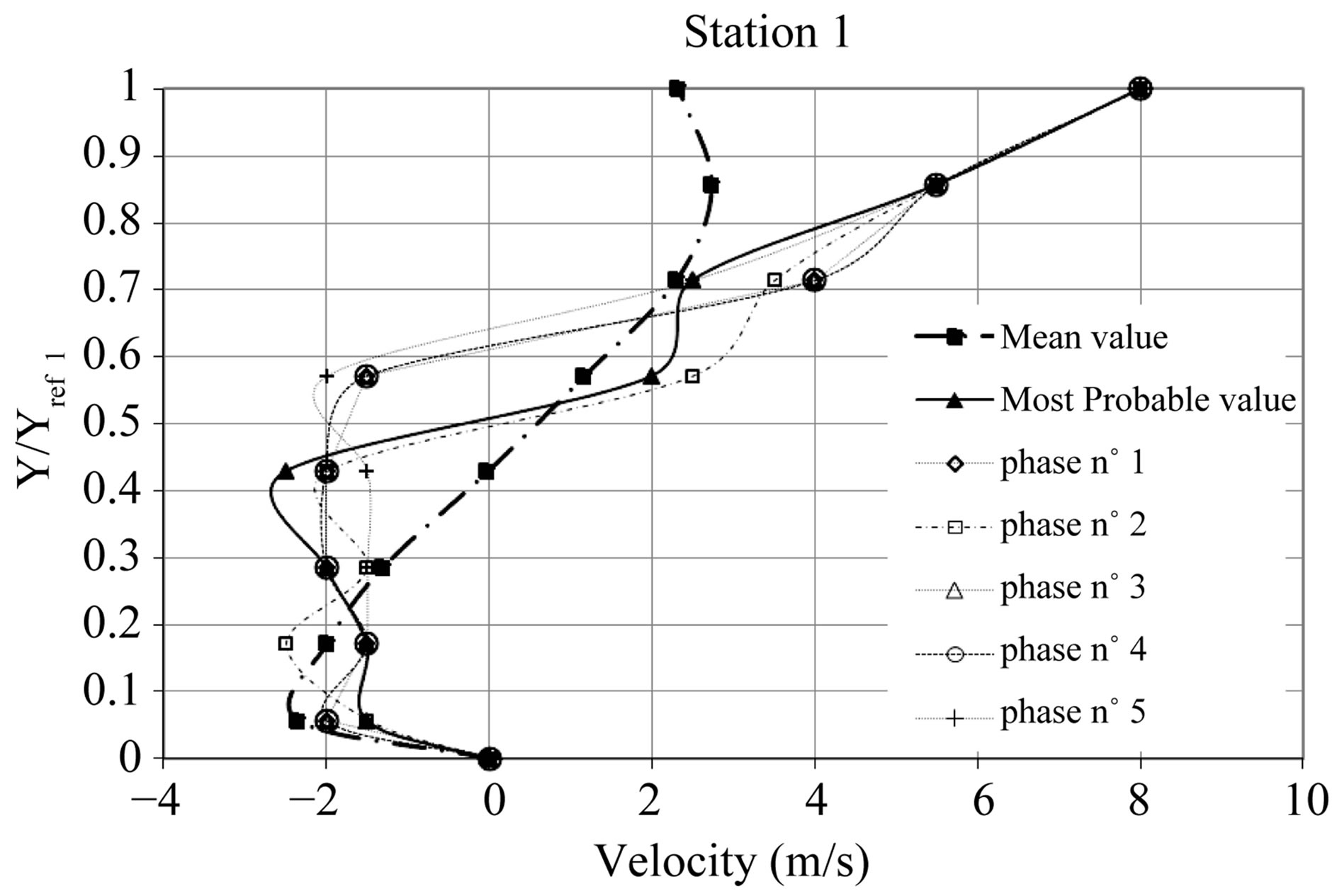
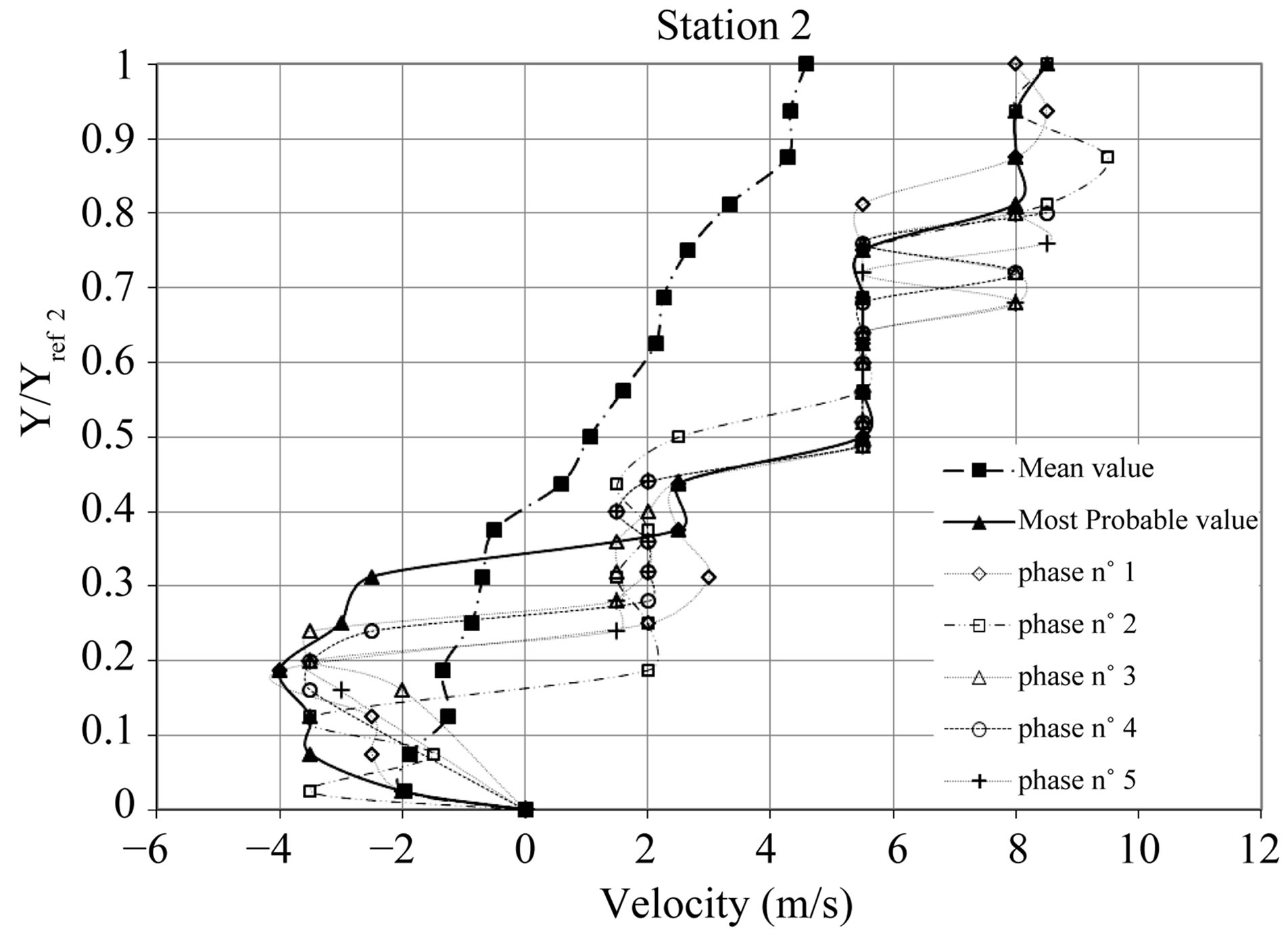
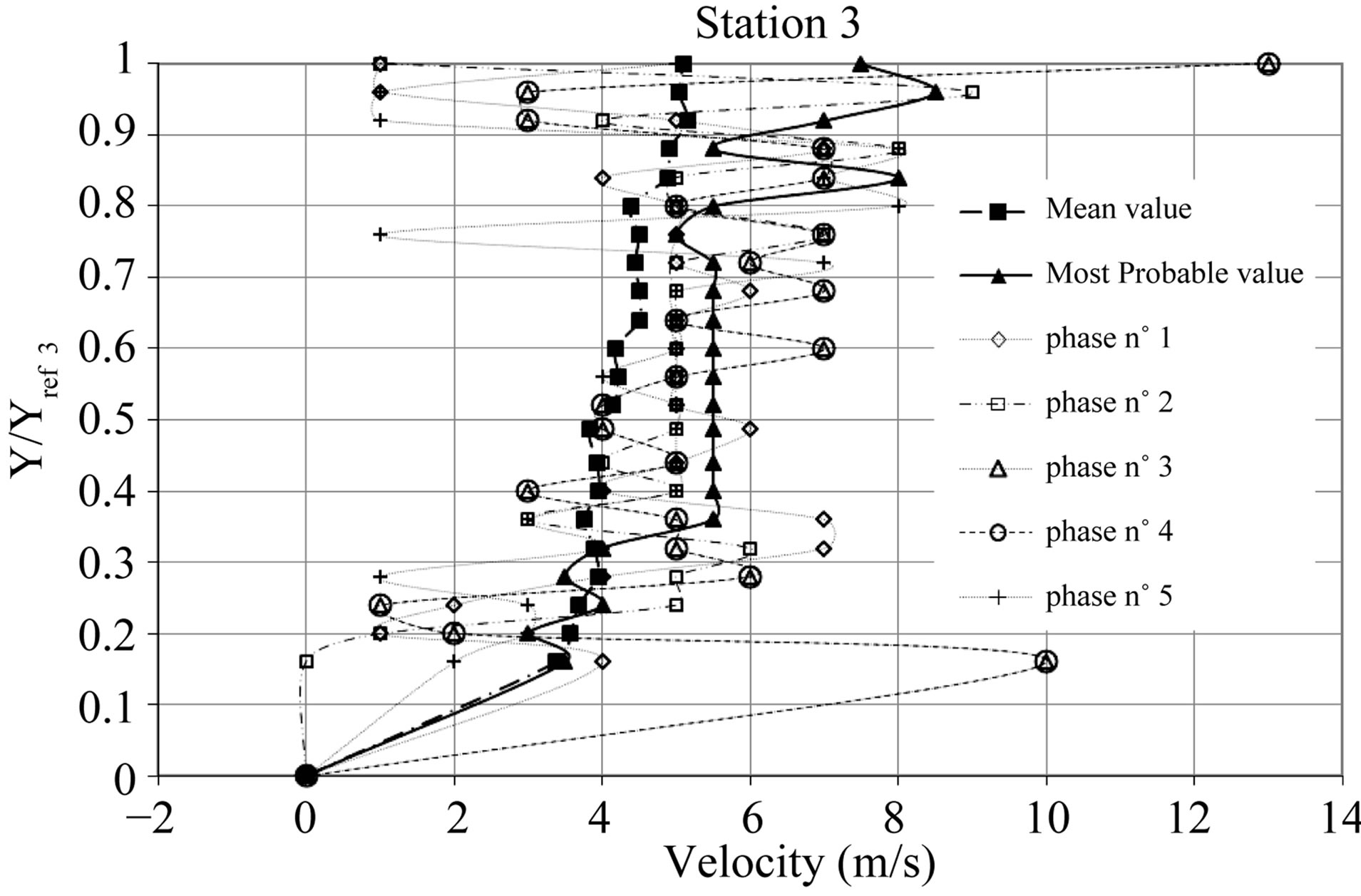
Figure 12. Velocity field inside the cavity. Comparisons with phase averaging analysis of the velocity field.
text of the present phase averaging analysis. At stations 1 and 2, the re-entrant jet is present during the whole cycle. We can also observe that the overall main feature of the cycling process relies on the fact that the re-entrant jet apparent thickness seems to evolve from one step to another. Velocity profiles lead us to describe the re-entrant jet dynamics. Indeed, the liquid gets inside the cavity from the downstream part between station 2 and 3. Then it vaporizes on the way to the throat. Finally, it changes direction and goes back swept along by the liquid above the cavity. As presented in Figure 13, the cavity can be dissected within three parts: the re-entrant jet, the upside part and convected structures.
4.3. Vapor Phase Dynamic inside the Cavity
The flow inside the cavity is turbulent, unsteady and quasi-periodic at a frequency close to 45 Hz. Fluctuations of the shape of the cavity have been observed showing that vapor clouds are convected by the liquid flow. The pressure has been measured at each station at the wall (station X1 to X8, and y = 0 mm). Pressure fluctuations are oscillating at a dominant frequency of 45 Hz for each location in the downstream part. Thanks to the pressure signal time reference it was possible to individually calculate the mean void ratio of each break-off cycle. With this data, an analysis of the void ratio field dynamics has been performed. The optical probe signals were then cut up using the pressure signal recorded in the downstream part as time reference to locate the beginning and the end of each break-off period. Figure 14 shows an example of the obtained void ratio for each period during a 40 s measurement which corresponds to about 2000 periods. In this case, the average void ratio is a = 0.64% (dotted line in Figure 15). The probability density function of the void ratio is plotted in Figure 16 for a cumulative data set of 10 measurements of 40 s each, giving a 400 s observation time.
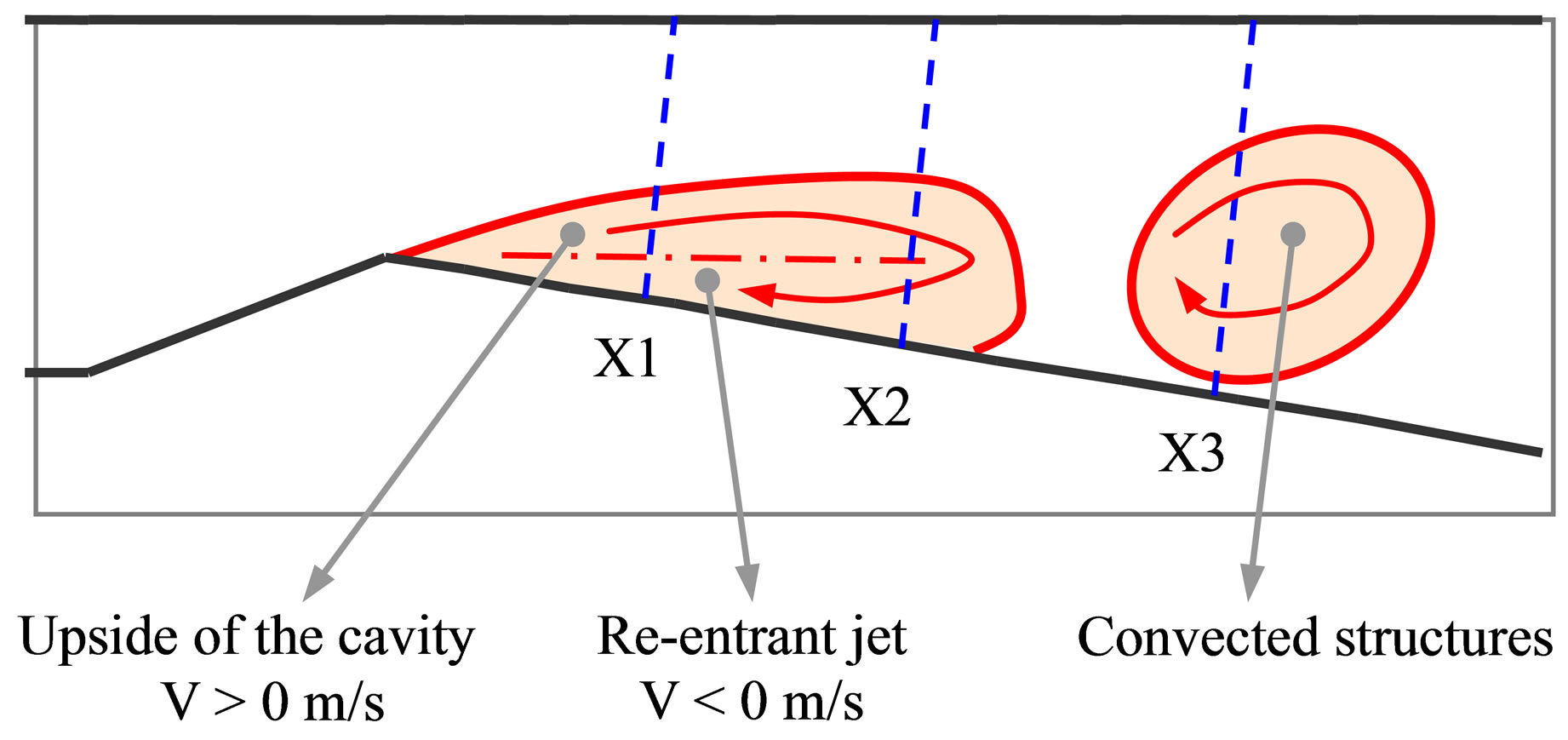
Figure 13. Sketch of the cavity structure.

Figure 14. Void ratio PDF of the period where bubbles have provided velocity measurement at location. X3 = 49.9 mm; Y = 8 mm (400 s measurement).
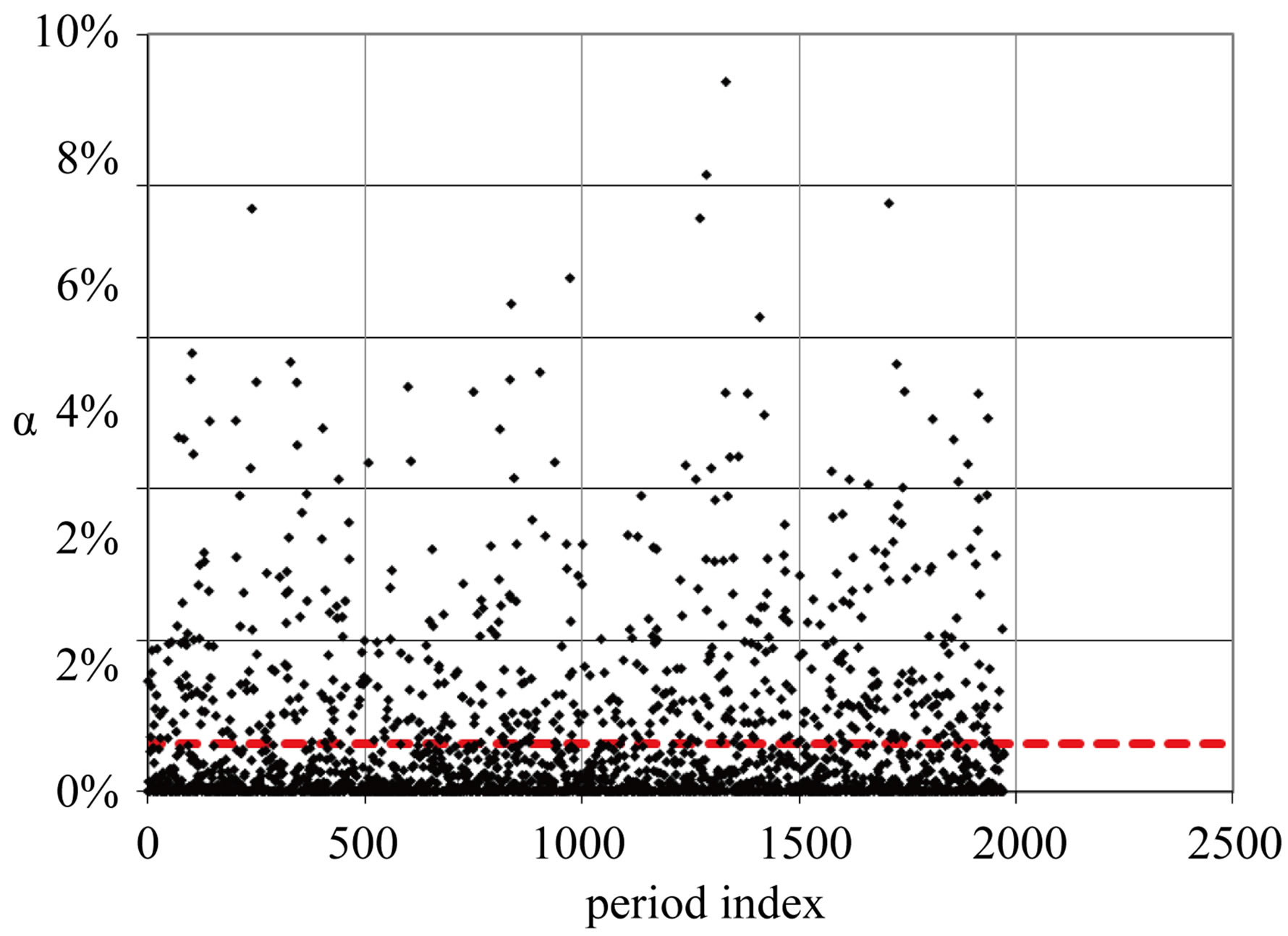
Figure 15. Period by period void ratio at location X3 = 49.9 mm; Y = 8 mm (40s measurement). - - - mean void ratio: 0.64%.

Figure 16. Period by period void ratio PDF at location X3 = 49.9 mm; Y = 8 mm (400 s measurement).
As shown in the Figures 15 and 16, period by period void ratio values cover a wide range from zero to about 10%. A sizeable number among all these periods exhibit a void ratio higher than five times the average which is 0.64%. The PDF shows that 43% of the periods have a void ratio lower than 0.1% whereas the averaged void ratio is 0.64% (dotted line in Figure 15). This conditional analysis shows that even though the pressure signal is periodic, the vapor formation is quite irregular. Nevertheless, it can be noticed that the velocity measurement method used in the present study may leads to some limitation especially during a period with a very low void fraction. Indeed, the present study was carried out with a homogeneous approach for the two phase flow. This means that the vapor and the liquid flow are supposed to run in the same direction at the same velocity (no-slip hypothesis). From that hypothesis we are able to describe the fluid velocity by measuring only the velocity of the vapor bubbles. So, more bubbles there are, more instantaneous velocity measurements are obtained. Therefore, by using our velocity measurement method, the high void ratio events provide more contribution to the velocity values determination than the others leading to a kind of bias. In order to quantitatively describe this effect we perform a conditional analysis of the void ratio field. Following this analysis, only the events (bubbles) leading to a validated velocity value (according to the method described in section 3.2 of the present paper) were used to calculate the conditional void ratio PDF. Figure 14 shows an example of this probability density function (PDF). The y-axis shows the number of bubbles which have provided a velocity value, the x-axis is the void ratio of the period where those specific bubbles have been observed. The averaged void ratio pondered by the occurrence number of velocity measurements obtained is then called the conditional void ratio.
The statistics show that no velocity measurements were obtained for period with void ratio lower than 0.1% which represents 43% of the events. Results have then to be observed carefully: velocity measurements for the studied location (X3, Y = 8 mm) seems to represent a category of events that is qualitatively different from the one obtained in the first analysis performed to compute the mean void ratio distribution. It then became questionable to characterize the behavior of the fluid inside the cavity from these data. To illustrate this, the conditional analysis has been carried out through the whole cavity.
For this purpose, the conditional void ratio has been computed for all the available measurements positions of the present experiment. Results are presented on Figures 17(a), (b) and (c) which display the conditional void ratio evolution for the three probed stations of the present study. The conditional void ratio is here compared to the continuous value obtained by a classical global averaging method as described in section 3.1 of the present paper.
This comparison shows that the estimated void ratio distributions are quite different and depend on the localization inside the cavity. It can be seen, for stations 1 and 3, a sizeable difference especially where the break-off cycle is predominant.
To sum up, the measured velocity is not representative of all events: it highlights high void ratio events. At the two first stations: velocity measurements come from events at a slightly higher void ratio than the average one. The corresponding velocity measurements are considered representative of the global dynamic behavior inside the cavity. In the third station case, a sizeable difference between the average and the conditional void ratio was observed. Therefore, the velocity field is characteristic of the events at high void ratio. It must be noticed that this study points out some limits of velocity measurements by optical probe technique in such unsteady two phases turbulent flow where void ratio is low (a < 1% at station 3).
The present measurements lead us to consider the
 (a)
(a)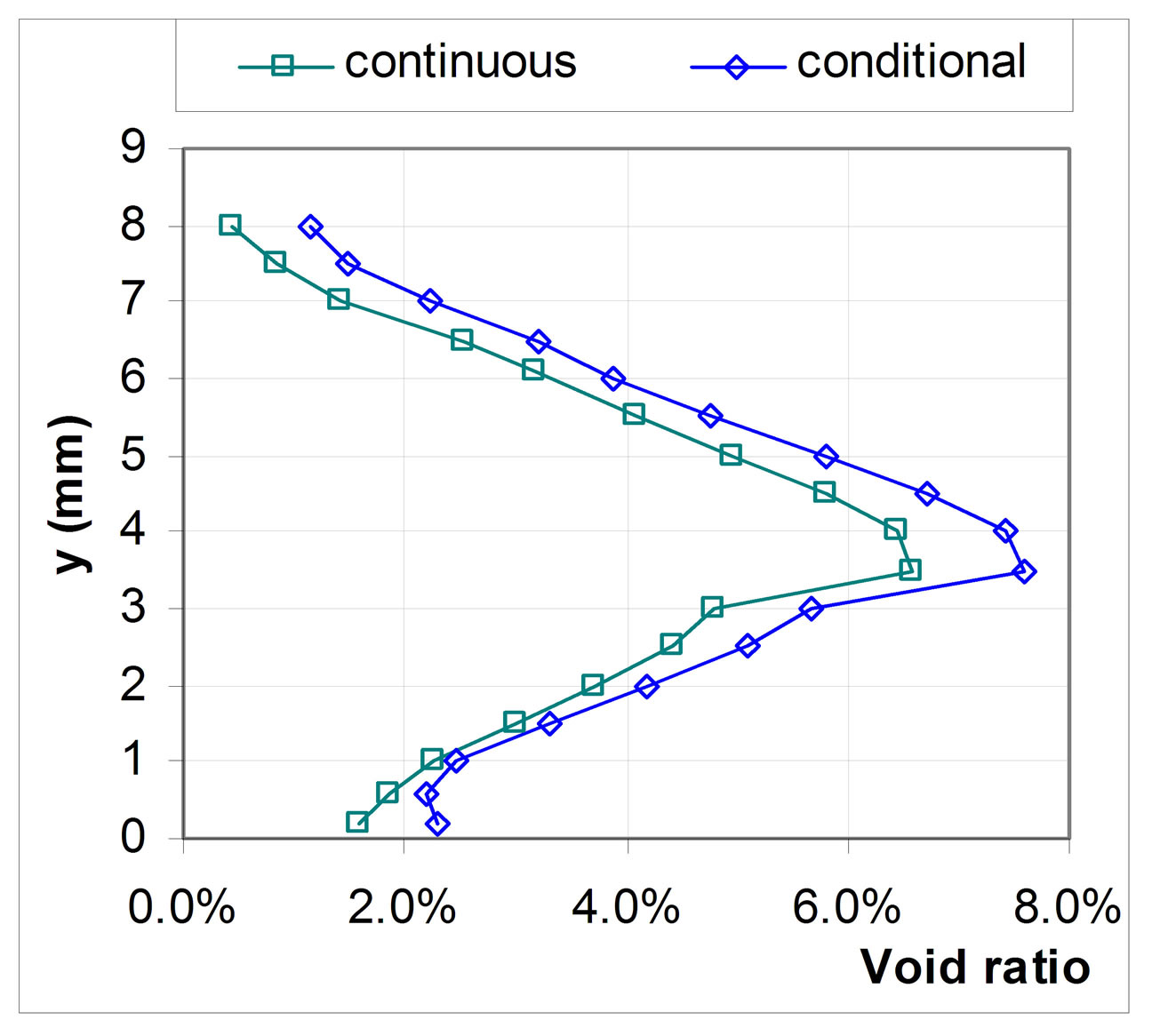 (b)
(b)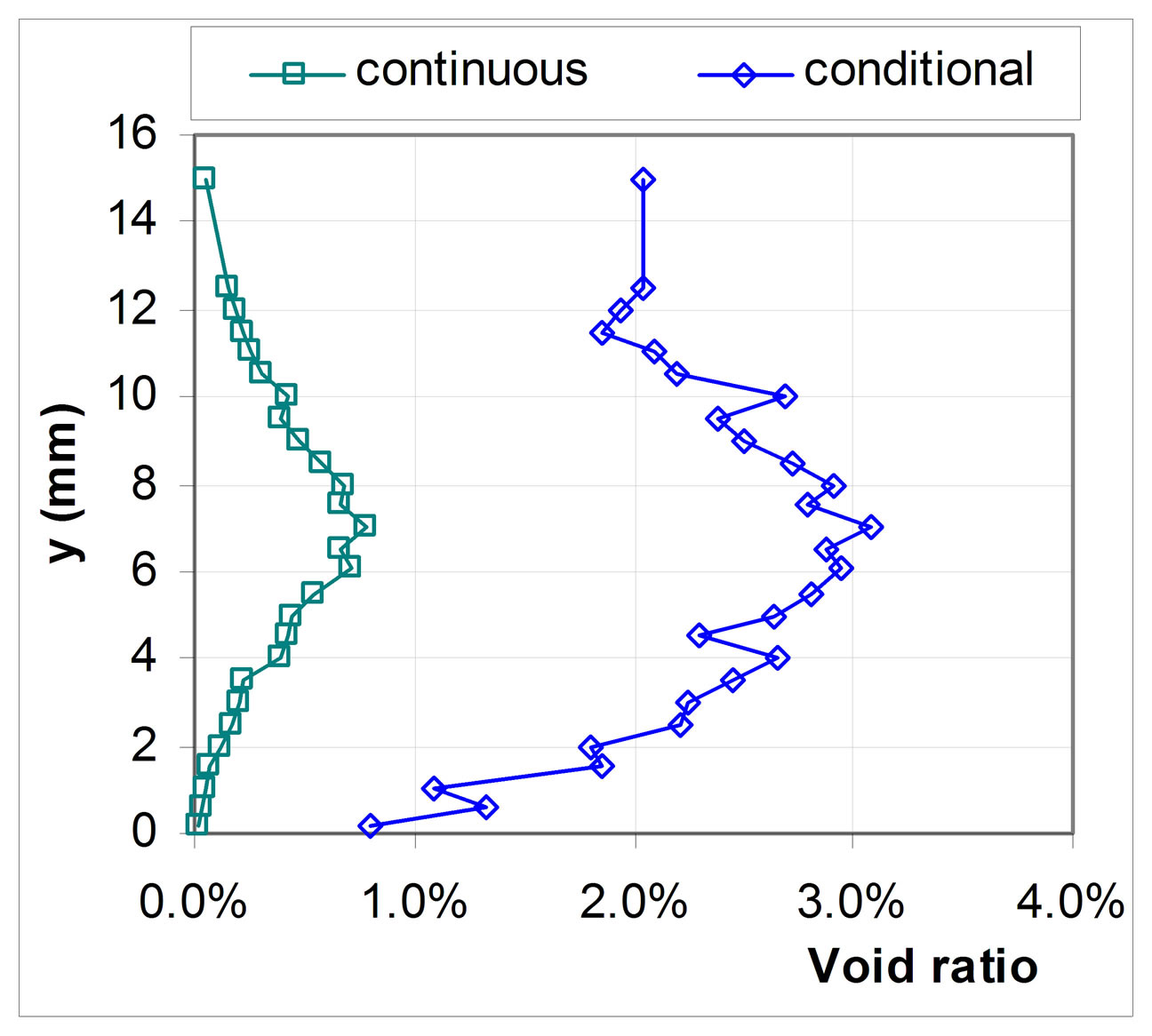 (c)
(c)
Figure 17. Comparison between mean and conditional values of the void ratio distribution.
mass and vapor flow rate inside the cavity. Indeed, from the integration of both the density and mean velocity field at a given section, we obtain the mass flow rate. For the two first sections studied, station 1 and 2, the respective values of 0.1 kg/s and 0.4 kg/s are obtained whereas at station 3 it is 2.2 kg/s (see Figure 18). When those values are compared to the mass flow rate through the whole duct, set at 15.5 kg/s, it appears that at station 1 and 2 they are negligible. It means that the re-entrant jet brings back as much fluid as the upper part of the cavity carries downstream. This behavior allows us to consider the border of the cavity as approximately a flow-line from the throat to the upper border of the cavity located

Figure 18. Illustration of the mass flow rate distribution.
at station 2.
The Figure 19 presents the vapor flow rate distribution inside the cavity which has been calculated by integration of the experimental mean velocity and the void ratio over each section. For the station 1 and 2 there are two values, one corresponding to the section in the re-entrant jet and the other one corresponds to the section where the velocity is positive.
The volume of vapor is not preserved from station 2 (4.2 cm3/s) to station 1 (2.4 cm3/s) within the re-entrant jet nor from station 1 (11.7 cm3/s) to station 2 (15.1 cm3/s) within the upper part of the cavity. So the bubbles are not carried from a station to the next one without changing size, collapsing or being created. It is also plausible that some bubbles cross the border of the re-entrant jet between station 1 and 2.
Contrary to the negligible mass flow rate in the 1st and 2nd section, the vapor flow rate is quite important: 9.3 cm3/s cumulated at station 1 and 10.9 cm3/s at station 2. The attached part of the cavity is producing vapor. From station 2 to station 3, the vapor flow rate decreases from 10.9 cm3/s to 8.1 cm3/s. This means that vapor clouds have already started to collapse when they cross the third section and probably some bubbles are re-injected inside the attached cavity by the re-entrant jet.
5. Conclusions
A quite complete experimental study of an unstable cavitation sheet in a 2D Venturi configuration has been performed by conditional and phase averaging approaches. Compared to previous works done in the same geometry, some important improvements both on the experimental method and data processing algorithms were carried out to obtain more precise and reliable results concerning void ratio and instantaneous velocity fields. A global analysis of the sheet pulsation cycle was performed and provided acceptable results. Indeed, both conditional and phase approaches led to characterize the dynamics of the void ratio topology during a break-off process and allowed us to highlight the re-entrant jet thickness and associated oscillating mechanism. Actually, the thickness of the cavity was almost constant during a break-off cycle instead of the void ratio fluctuations in
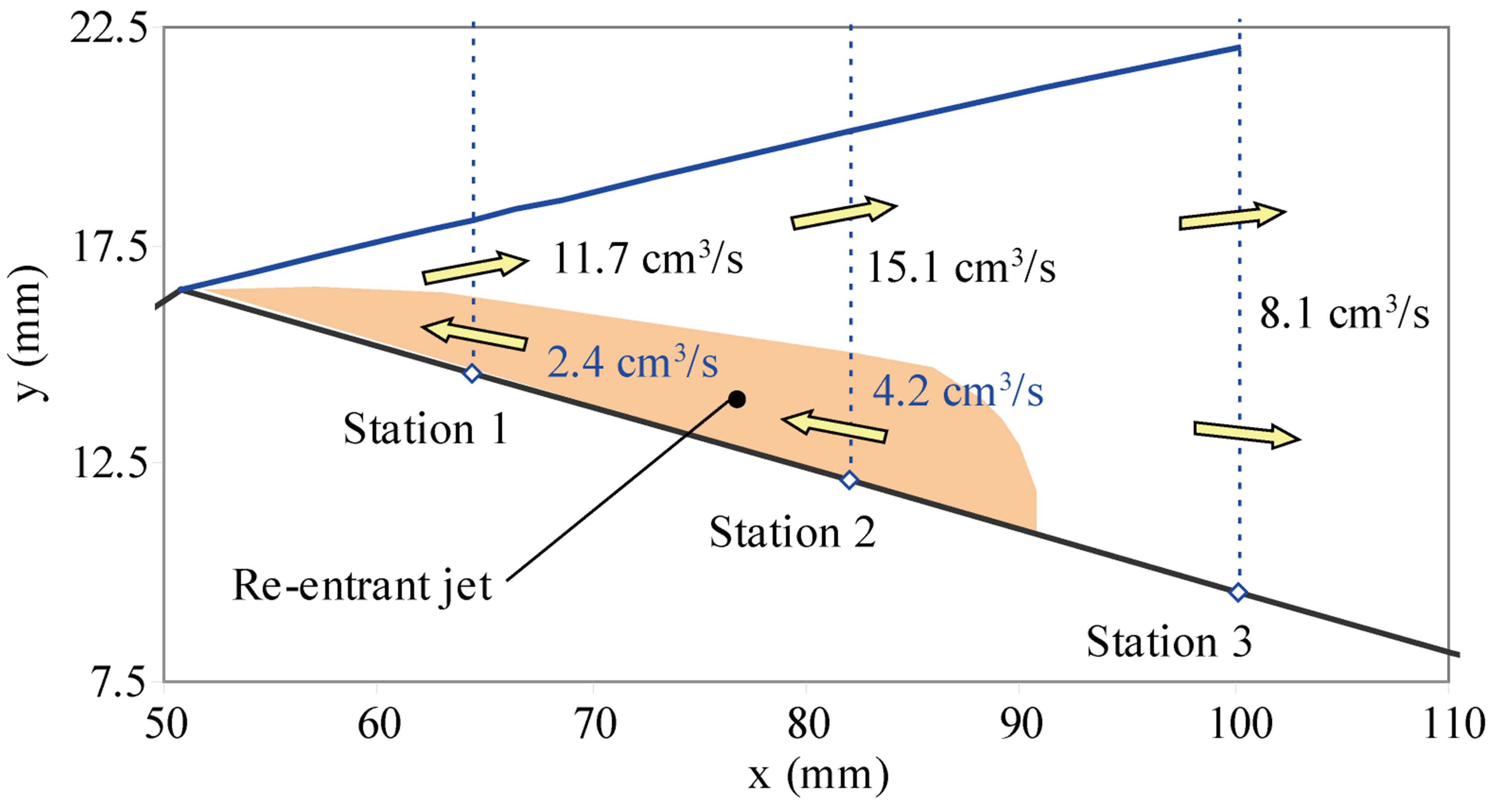
Figure 19. Illustration of the vapor flow rate repartition.
the re-entrant jet area and in the upper part of the cavity were in phase. By comparison with the classical mean estimation, the re-entrant jet is more extended where unsteadiness is more pronounced. Moreover, by performing a local and unsteady analysis of the void ratio and velocity fields, the study shows that there is no agreement between mean and conditional most probable approaches, concerning void ratio and velocity field distributions inside the attached cavitation sheet.
To conclude, each cycle of break-off mechanism of the cavity got different magnitude and the link between the void ratio and the pressure may not be direct and independent of the instantaneous transports dynamics characteristics of the flow.
As a perspective of the present work, it can be admitted that the present velocity determination method using double optical probe is found to be strongly affected by some bias when used in flows experiencing a high void ratio fluctuations level. This result leads us to completely change our measurement strategy for the next works dealing with high Reynolds number turbulent cavitating flows. PIV-LIF measurements are then developed to measure mean velocity fields and Reynolds stress tensor in this kind of flows (see Aeschlimann et al. [20]). We also move to X-Ray absorption techniques in order to measure mean and fluctuating void rate fields (see Aeschlimann et al. [21]). The future direction of this field of researches will be analyzing the spatio-temporal dynamic of the liquid and vapor phase simultaneously using optical methods. The future database will be available in order to test URANS and/or LES approaches in this class of flow where turbulence and cavitation interact.
6. Acknowledgements
The authors wish to express their gratitude to the French space agency CNES and to the SNECMA company for their continuous support.
REFERENCES
- K. Kamijo, T. Shimura and M. Watanabe, “An Experimental Investigation of Cavitating Inducer Instability,” ASME Winter Annual Meeting, Atlanta, 27 November- 2 December 1977.
- J. De Bernardi, F. Joussellin and A. Von Kaenel, “Experimental Analysis of Instabilities Related to Cavitation in Turbopump Inducer,” Proceedings of 1st International Symposium on Pumps Noise and Vibration, Paris, 7-9 July 1993, pp. 91-99.
- W. Hassan, S. Legoupil, D. Chambellan and S. Barre, “Dynamic Localization of Vapor Fraction in Turbopump Inducers by X-Ray Tomography,” IEEE-TNS (Transaction on Nuclear Sciences), Vol. 55, No. 1, 2008, pp. 656- 661.
- B. Stutz and J. L. Reboud, “Two-Phase Flow Structure of Sheet Cavitation,” Physical Fluids, Vol. 9, No. 12, 1997, pp. 3678-3686. doi:10.1063/1.869505
- B. Stutz, “Analyse de la Structure Diphasique et Instationnaire de Poches de Cavitation,” Ph.D. Thesis, INPG, CREMHYG Laboratory, Grenoble, 1996.
- B. Stutz, “Influence of Roughness One the Two-Phase Flow Structure of Sheet Cavitation,” Journal of Fluids Engeneering, Vol. 125, No. 4, 2003, pp. 652-659. doi:10.1115/1.1596240
- S. Barre, J. Rolland, G. Boitel, E. Goncalves and R. Fortes Patella, “Experiments and Modelling of Cavitating Flows in Venturi: Attached Sheet Cavitation,” European Journal of Mecanics B/Fluids, Vol. 28, No. 3, 2009, pp. 444-464.
- O. Coutier-Delgosha, J.-L. Reboud and Y. Delannoy, “Numerical Simulation of the Unsteady Behavior of Cavitating Flows,” International Journal for Numerical Methods in Fluids, Vol. 42, No. 5, 2003, pp. 527-548.
- J. L. Reboud, R. Fortes-Patella, M. Hofmann, H. Lohrberg, G. Ludwig and B. Stoffel, “Numerical and Experimental Investigations on the Self-Oscillating Behavior of Cloud Cavitation,” ASME-FEDSM 99-6755/7259, San Francisco, 1999.
- E. Goncalves and R. Fortes-Patella, “Numerical Simulation of Cavitating Flows with Homogeneous Models,” Computers & Fluids, Vol. 38, 2009, pp. 1682-1696. doi:10.1016/j.compfluid.2009.03.001
- E. Goncalves and R. Fortes-Patella, “Constraints on Equation of State for Cavitating Flows with Thermodynamic Effects,” Applied Mathematics and Computation, 2010, in Press.
- E. Goncalves, “Numerical Study of Expansion Tube Problems: Toward the Simulation of Cavitation,” Computers and Fluids, Vol. 72, 2013, pp. 1-19. doi:10.1016/j.compfluid.2012.11.019
- J. Decaix and E. Goncalves Da Silva, “Compressible Effects Modelling in Turbulent Cavitating Flows,” European Journal of Mechanics B/Fluids, Vol. 39, 2013, pp. 11-31. doi:10.1016/j.euromechflu.2012.12.001
- B. Stutz and J. L. Reboud, “Experiments One Unsteady Cavitation,” Experiments in Fluids, Vol. 22, 1997, pp 191-198.
- B. Stutz and J. L. Reboud, “Measurements within Unsteady Cavitation,” Experiments in Fluids, Vol. 29, No. 6, 2000, pp. 545-552. doi:10.1007/s003480000122
- N. Dittakavi, A. Chunekar and S. Frankel, “Large Eddy Simulation of Turbulent-Cavitation Interactions in a Venturi Nozzle,” Journal of Fluid Engineering, Vol. 132, 2010, Article ID: 121301.
- F. De Lange and J. De Bruin, “Sheet Cavitation and Cloud Cavitation, Re-Entrant Jet and Three-Dimensionality,” Applied Scientific Research, Vol. 58, No. 1-4, 1998, pp. 91-114. doi:10.1023/A:1000763130780
- E. J. Foeth and T. V. Terwisga, “The Structure of Unsteady Cavitation. Part I: Observation of an Attached Cavity on a Three-Dimensional Hydrofoil,” 6th International Symposium on Cavitation, Wageningen, 11-15 September 2006.
- R. Fortes-Patella, O. Coutier-Delgosha, J. Perrin and J.-L. Reboud, “A Numerical Model to Predict Unsteady Cavitating Flow Behavior in Inducer Blade Cascades,” Journal of Fluid Engineering, Vol. 129, No. 2, 2007, pp. 128- 135. doi:10.1115/1.2409320
- V. Aeschlimann, S. Barre and H. Djeridi, “Velocity Field Analysis in an Experimental Cavitating Mixing Layer,” Physics of Fluids, Vol. 23, 2011, Article ID: 055105.
- V. Aeschlimann, S. Barre and S. Legoupil, “X-Ray Absorption Measurements in a Cavitating Mixing Layer for Instantaneous 2D Void Ratio Determination,” Physics of Fluids, Vol. 23, 2011, Article ID: 055101.

