Open Journal of Applied Sciences
Vol.05 No.09(2015), Article ID:60017,11 pages
10.4236/ojapps.2015.59054
An Econometric Analysis of Hospital Length of Stay for Cataract Operations in Japan by the Box-Cox Transformation Model and Hausman Tests: Evaluation of the 2010 Revision of the Medical Payment System*
Kazumitsu Nawata1, Koichi Kawabuchi2
1Graduate School of Engineering, University of Tokyo, Tokyo, Japan
2Graduate School of Medical and Dental Sciences, Tokyo Medical and Dental University, Tokyo, Japan
Email: nawata@tmi.t.u-tokyo.ac.jp
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 25 August 2015; accepted 26 September 2015; published 29 September 2015
ABSTRACT
The Japanese medical costs for cataract treatments reached 270 billion yen in fiscal year 2012. Since the length of stay (LOS) in hospital is much longer than other major countries, controlling the medical costs by reducing LOS becomes an important issue in Japan. In this paper, we evaluated the effects of the 2010 revision of the Japanese medical payment system (DPC/PDPS) on LOS for cataract operations. The Box-Cox transformation model, Nawata’s estimators and Hausman tests were used in the analysis. To evaluate the effects, we analyzed a dataset obtained from 34 DPC hospitals (Hp1-34) where one-eye cataract operations were performed both before (April 2008-March 2010) and after (April 2010-March 2012) the 2010 revision and there were more than 500 patients. The dataset contained information from 32,593 patients. We did not admit the effect of the 2010 revision in this study, and there were large differences LOS among hospitals, even after removing the influences of factors such as patient characteristics and types of principal diseases.
Keywords:
Diagnosis Procedure Combination (DPC), Cataract, Length of Stay (LOS), Box-Cox Transformation Model

1. Introduction
A medical inclusive payment system based on the diagnosis procedure combination (DPC) was introduced in April 2003. The DPC classified diseases, treatments and conditions of patients by 14 digits and was originally developed in Japan. The DPC-based inclusive payment has been called the DPC/PDPS (DPC/per diem payment system) since December 2010 [1] . As of April 2013, a total of 1496 hospitals (hereafter DPC hospitals), comprising about 20% of all general hospitals in Japan, had joined the DPC/PDPS. These hospitals had 474,981 beds, more than half of the total number of beds in all general hospitals [2] . For details of the DPC/PDPS, see Nawata et al. [3] . Since DPC hospitals are required to satisfy certain rather costly conditions [4] , it is difficult for small hospitals to join the DPC/PDPS. As a result, the percentage of DPC hospitals increases as the hospital size becomes larger. For example, among small hospitals with fewer than 100 beds, just about 5% were the DPC hospitals. On the other hand, among large hospitals with 500 or more beds, nearly two thirds were the DPC hospitals [2] . The revisions of DPC/PDPS have been implemented every other year. However, sufficient evaluations of the system have not yet been conducted for these revisions. Empirical studies of hospital length of stay (LOS) using econometric models are necessary to evaluate the system correctly.
According to the Ministry of Health, Labour and Welfare [5] , the medical costs for cataract were 270 billion yen in fiscal year (April-March) 2012 in Japan. The 76,577 cataract operations were done for 48,235 cases and their direct costs were 8.03 billion yen in June 2012 [6] . In Japan, two-eye cataract operations, in which both eyes are operated on during a single period of hospitalization, are also performed. Therefore, the number of operations becomes larger than that of cases. It is estimated that about 920 thousand cataract operations costing nearly 100 billion yen are done annually. Cataract operations are usually carried out on a same-day basis, without any hospitalization in major countries ( [7] , pp. 100-101). The long LOS is one of the most noticeable characteristics of cataract operations and controlling medical costs by reducing LOS is a very important issue in Japan.
In this paper, we evaluate the effects of the 2010 revision of the DPC/PDPS on LOS for cataract operations using the Box-Cox [8] transformation model (hereafter, BC model), estimators proposed by Nawata [9] [10] and Hausman tests. The BC model is widely used to examine various econometric problems especially when the distribution has a heavy tail on the right side. For details and examples of the BC model, see Hossain [11] and Sakia [12] . The maximum likelihood estimator under the normality assumption (hereafter, BC MLE) is used for the estimation of the BC model. Since the BC model is just a simple regression model when the transformation parameter is given, it can be easily estimated by the least squares and scanning methods. However, the BC MLE is not generally consistent. Various researchers have proposed alternate methods of the BC model and BC MLE [13] -[15] . However, since their methods are rather complicated [16] , they have not been widely used. Although the BC MLE is generally inconsistent, it can be a consistent estimator if the error terms are homoscedastic and the “small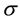 ” assumption [17] is satisfied. Nawata [9] proposed a new consistent estimator of the BC model. However, the estimator is inconsistent if the error terms are heteroscedastic. Large biases of the BC MLE under heterogeneity were reported [16] . Therefore, heteroscedasticity is a very important problem in the BC model. Especially, for the LOS, variances are often very different even among hospitals. Powell [18] proposed a semiparametric estimator based on the moment restriction. Although Powell’s estimator is consistent with heteroscedasticity, it performs quite poorly. More recently, Nawata [10] proposed an estimator that was consistent with heteroscedasticity.
” assumption [17] is satisfied. Nawata [9] proposed a new consistent estimator of the BC model. However, the estimator is inconsistent if the error terms are heteroscedastic. Large biases of the BC MLE under heterogeneity were reported [16] . Therefore, heteroscedasticity is a very important problem in the BC model. Especially, for the LOS, variances are often very different even among hospitals. Powell [18] proposed a semiparametric estimator based on the moment restriction. Although Powell’s estimator is consistent with heteroscedasticity, it performs quite poorly. More recently, Nawata [10] proposed an estimator that was consistent with heteroscedasticity.
Using Nawata’s [9] [10] estimators, Hausman [19] tests are done for the BC MLE; that is, we determine whether or not we can use the BC MLE for the estimation of the BC model. Hausman tests compare two (vectors of) estimators, 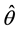 and
and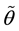 .
.  is consistent with the null hypothesis but inconsistent with alternative hypothesis, and
is consistent with the null hypothesis but inconsistent with alternative hypothesis, and 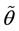 is consistent both with null and alternative hypotheses. The test statistic is given by
is consistent both with null and alternative hypotheses. The test statistic is given by 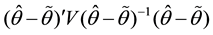 and its asymptotic distribution is the chi-square distribution with degrees of freedom
and its asymptotic distribution is the chi-square distribution with degrees of freedom  under the null hypothesis where
under the null hypothesis where  is the dimension of
is the dimension of  and
and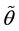 .
.
In the case of cataract operations, major changes were made concerning the DPC classifications and the inclusive payments determined by the DPC/PDPS in the 2010 revision. To evaluate these changes, we analyzed the dataset obtained from 34 DPC hospitals (Hp1-34) where one-eye cataract operations were performed both before (April 2008-March 2010) and after (April 2010-March 2012) the 2010 revision, and more than 500 patients were operated in the sample period. The dataset of 32,593 patients were used in the analysis.
2. Estimators of the BC Model
2.1. BC Model
Suppose that LOS of patient t is given by the BC model.
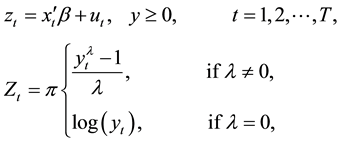 (1)
(1)
where 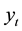 is the LOS,
is the LOS, 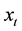 and
and 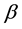 are the vectors of the explanatory variables and coefficients, respectively, and
are the vectors of the explanatory variables and coefficients, respectively, and 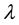 is the transformation parameter. The likelihood function under the normality assumptions is given by
is the transformation parameter. The likelihood function under the normality assumptions is given by
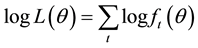 , and
, and
where 



be the true parameter values of



it is referred to as the “small
cient estimator, and “small


where

2.2. N-Estimator
Nawata [9] considered the roots of the equations,







Therefore, we get

If the third moments of 



where


2.3. Robust Estimator
The N-estimator is not consistent under heteroscedasticity. Nawata [10] proposed a robust estimator that is consistent even under heteroscedasticity if the first and third moments are zero. The estimator is obtained from the roots of the equations,



where






where


3. Hausman Tests for the BC Model
3.1. A Test of the Homoscedasticity and “Small σ” Assumptions
We first test the null hypothesis consisting of the homoscedasticity and “small


where 

Let 



we can test this assumption using 
3.2. A Test of Homoscedasticity
The N-estimator is not consistent under heteroscedasticity. Therefore, it is necessary to test the homoscedasticity assumption if the null hypothesis in the previous section is rejected. The null hypothesis is homoscedasticity. For this test, we use the N-estimator and robust estimator. Under the null hypothesis,


where c and f are the first columns of 



where



4. Data and Summary of the 2010 Revision for Cataract Operations
4.1. Data
In this study, we use data from the Section of Health Care Economics of Tokyo Medical and Dental University. The data were collected from over 100 Japanese hospitals between 2008 and 2012, from April to March of each fiscal year. Various information (nearly 200 items) for individual patients was available. More precisely, we could get information of patients’ genders and ages, dates of hospitalization, medical costs, DPC code, International Classification of Diseases 10th revision (ICD-10) codes determined by the World Health Organization (WHO) for the principal diseases, medical treatments and operations, comorbidities, complications, and placements after hospitalization [12] . The ICD-10 codes classify diseases by one alphabet and three digit numbers.
We considered only patients who underwent one-eye cataract operations without secondary treatments of article kidney. The DPC codes for this procedure were 020110xx97x0x0 and 020110xx97xxx0 before (April 2008-March 2010) and after (April 2010-March 2012) the 2010 revision. The original dataset contained information from 42,925 patients. Since the distribution of LOS had a heavy tail on the right side as shown in Figure 1, we used the BC model rather than the ordinary least squares model. Among these patients, we used the data-
set obtained from 34 DPC hospitals (Hp 1-34) where operations were performed both before and after the revision to evaluate the effect of the 2010 revision of the DPC/PDPS, and where more than 500 were operated in the sample period. These hospitals had 32,595 patients. Table 1 shows LOS by hospital. The average length of stay (ALOS) was 3.51 days and the standard deviation was 2.84 days for all 32,595 patients. The maximum ALOS by hospital was 6.12 days (Hp 23), and the minimum was 2.0 days (Hp 11). The maximum was more than 4 days longer than the minimum, and there were large differences among hospitals.
4.2. Summary of the 2010 Revision for Cataract Operations
The 2010 revision of the DPC/PDPS contained major changes for cataract operations. Before the revision, dif-
Figure 1. Distribution of LOS.
Table 1. LOS by hospital.
S.D.: Standard Deviation.
ferent DPC codes were assigned depending on the presence or absence of secondary treatments of article kidney (without secondly treatments 020110xx97x0x0; with secondly treatments: 020110xx97x1x0), and the medical payments differed accordingly. After the revision, cataract operations were categorized under just one DPC code (020110xx97xxx0) independent of the presence of secondary treatments of article kidney.
The Periods I and II and the Specific Hospitalization Period were changed, and the per diem inclusive payments were revised. The per diem inclusive payment in 2008-9 for patients without the secondary treatments was 2363 points for the first day, 1900 points for the 2nd and 3rd days, and 1615 points for the 4th-7th days. For those with the secondary treatments, the per diem inclusive payment was 2829 points up to the 2nd day, 2091 points for the 3rd and 4th days, and 1777 points for the 5th-7th days. After the revision, the per diem inclusive payment became 2237 points up to the 2nd day, 1627 points for the 3rd day, and 1464 points for the 4th-6th days for all cataract patients independent of the secondary treatments (10 yen per point are paid to a hospital.)
5. Results of Estimation
When we analyze LOS, we need to consider the characteristics of the patients and the types of principal disease
as the explanatory variables. The data of 32,923 patients without missing values in explanatory variables were used for the analysis. For the gender of patients, we used a Female dummy (1: female; 0: otherwise). The percentage of female patients was 56.3%. Costs of hospitalization (including opportunity costs) tend to decrease with patient age. Therefore, we used Age (age of a patient) as an explanatory variable. Japan has employed the public health insurance system and all Japanese have been required to attend some types of the insurances. During the sample period, percentages of direct payments by patients changed at age 70; that is, 10% for patients age 70 or older and 30% for patients younger than age 70. Therefore, we added Age 70 (1: age 70 or over; 0: otherwise) dummy. (Note that the payments of patients have been increased to 20% for patients age 70 - 74 since April 2014.) The average and standard deviation of ages were 73.6 and 10.0, respectively. For representing conditions of patients, Comorbidities (number of comorbidities), Complications (number of complications), and Non-planned (1: hospitalization was not planned in advance; 0: otherwise), Outpatient (1: patient was outpatient before hospitalization; 0: otherwise) and Other Hospital (patient was introduced by another hospital; 0: otherwise) dummies were used. 45.4% and 38.1% of patients had comorbidities and complications, respectively. The average numbers of comorbidities and complications were 1.77 and 1.40, respectively, for these patients. 0.67%, 92.4% and 45.4% of patients were non-planned hospitalizations, outpatients and introduced by other hospitals, respectively.
To analyze the impact of seasonal climates, we used Winter (1: winter, December to February; 0: otherwise) and Summer (1: summer, July and August; 0: winter) dummies. The percentages of patients treated in winter and summer were 20.9% and 22.4%, respectively. To analyze influences of the 2010 revision of the DPC/PDPS, After 2010 dummy (1: after April 2010; 0: otherwise) was used. 54.6% of patients were operated after April 2010. Trend (time trend) was added to evaluate the progress and improvement of cataract operation technologies. If the LOS exceeds the Specific Hospitalization Period, the payment system becomes the conventional fee- for-service system. Therefore, we added the Specific Period dummy (1: over the Specific Hospitalization Period, 0: otherwise) and 1.0% of patients stayed over the Specific Hospitalization Period.
Principal Disease dummies based on the ICD-10 codes were used to analyze the effects of principal diseases. The definitions and percentages of patients were as follows. H25.0: senile incipient cataract, 53.0%; H25.1: senile nuclear cataract, 16.7%; H25.2: senile cataract, morgagnian-type, 1.2%; H25.8: other senile cataract, 5.5%; H25.9: senile cataract, unspecified, 5.9%; H26.0: infantile and juvenile cataract, 6.2%; H26.9 (unspecified cataract) 8.3%; H26_other: other H26 cataracts including H26.2: complicated cataract, H26.3: drug-induced cataract, H26.4: After-cataract; H26.8: other specified cataract, 0.5%; H27: Other disorders of lens 0.9%; and H28: Diabetic cataract 1.7%. The base of the ICD-10 dummies was H25.0. Thirty four hospital dummies (1: Hp k; 0: otherwise) were used to represent the influence of the hospital. To evaluate the effects of hospitals directly, we used 34 hospital dummies and a constant term is not included.
Thus 

Tables 2-4 present the results of the estimation by the BC MLE, N-estimator and robust estimators. The estimates of the transformation parameters were








homoscedasticity was accepted at the 5% significance level. Therefore, the remainder of this paper was thus an analysis of the results of the N-estimator.
The estimate of 
Table 2. Results of estimation (BC MLE).
S.E.: Standard Error.
Table 3. Results of estimation (N-estimator).
S.E.: Standard Error; *Significant at the 5% level; **Significant at the 1% level.
For the estimates of the Hospital dummies, the maximum was 2.887 (Hp 25) and the minimum was 0.962 (Hp 5); the difference between the maximum and minimum values was 1.925 and it was much larger than the estimates of other variables except the Specific Period dummy. This indicated that there remained large differences among hospitals, even after removing the influences of factors such as patient characteristics, types of principal diseases and the revision of the DPC/PDPS. Although the medical society may express strong disapproval, it may be necessary to give hospitals additional strong incentives suggested by Nawata et al. [3] to reduce LOS in the future
Table 4. Results of estimation (robust estimator).
S.E.: Standard Error.
revision of the DPC/PDPS.
6. Conclusions
In this paper, we analyzed the effect of the 2010 revision of the DPC/PDPS on LOS for single-eye cataract operations (DPC category code 020110) in Japan using the BC model. The dataset contained information for 32,973 patients collected from 34 DPC hospitals where cataract operations were reported both before and after the 2010 revision and there were more than 500 patients. The sample period was from April 2008 to March 2012. We first performed the Hausman tests to determine whether or not we could use the BC MLE using Nawata’s [9] [10] estimators. We found that the null hypothesis consisting of the homoscedasticity and “small
Our results indicated that the factors which affected the LOS were the gender, age, comorbidities and complications, introduced by other hospitals, winter, time trend and Specific Hospitalization Period. As principal diseases, we found that H25.1, H25.2, H25.8 and H27 were significant. The ALOS values were significantly different among hospitals, even after removing the influences of patient characteristics and types of principal diseases. The estimate of After 2010 dummy was not significant, so we did not admit the effect of the 2010 revision in this study. Since the LOS of Japanese hospitals is quite long among major countries, incentives to hospitals to reduce their ALOS are very important. However, desirable incentives have not been known yet. These are subjects for future studies.
Acknowledgements
This study was supported by a Grant-in-Aid for Scientific Research on the subject of “Analyses of Large Scale Medical Survey Data and the Policy Evaluations in Japan (Grant Number: 24330067),” from the Japan Society of Science. The Institutional Review Boards of the University of Tokyo (number: KE12-7) and Tokyo Medical and Dental University (number: 839) approved the use of this dataset. We would like to thank an anonymous referee for his/her helpful comments and suggestions.
Cite this paper
KazumitsuNawata,KoichiKawabuchi, (2015) An Econometric Analysis of Hospital Length of Stay for Cataract Operations in Japan by the Box-Cox Transformation Model and Hausman Tests: Evaluation of the 2010 Revision of the Medical Payment System*. Open Journal of Applied Sciences,05,559-570. doi: 10.4236/ojapps.2015.59054
References
- 1. DPC Evaluation Division, Central Social Insurance Medical Council (2010) Heisei 24 nendo kaite ni muketa DPC seido (DPC/PDPS) no taiou ni tsuite (Concerning the Procedures for the 2012 Revision of the DPC System (DPC/PDPS)). (In Japanese)
- 2. DPC Evaluation Division, Central Social Insurance Medical Council (2013) DPC taishou hyouin junbi hyouin no gennjou ni tsuite (Current Situations of DPC Hospitals and Preparing Hospitals). (In Japanese)
- 3. Nawata, K., Ii, M., Toyama, H. and Takahashi, T. (2009) Evaluation of the Inclusive Payment System Based on the Diagnosis Procedure Combination with Respect to Cataract Operations in Japan. Health, 1, 93-103. http://dx.doi.org/10.4236/health.2009.12016
- 4. Nawata, K. and Kawabuchi, K. (2015) Evaluation of Length of Hospital Stay Joining Educational Programs for Type 2 Diabetes Mellitus Patients: Can We Control Medical Costs in Japan?” Health, 7, 256-269. http://dx.doi.org/10.4236/health.2015.72030
- 5. Ministry of Health, Labour and Welfare (2014) Hesiei 24 nendo kokumin iryouhi no gaikyou (Summaries of National Medical Expenditures in Fiscal Year 2012). (In Japanese)
- 6. Ministry of Health, Labour and Welfare (2013) Shakai iryou shinryu koui betsu chosa hesiei 24 nendo (Social Medical Surveys by Treatment Practices in Fiscal Year 2012). (In Japanese)
- 7. OECD (2013) Health at a Glance 2013. http://www.oecd-ilibrary.org/social-issues-migration-health/data/oecd-health-statistics_health-data-en
- 8. Box, G.E.P. and Cox, D.R. (1964) An Analysis of Transformations. Journal Royal Statistical Society Series B, 26, 211- 252.
- 9. Nawata, K. (2013) A New Estimator of the Box-Cox Transformation Model Using Moment Conditions. Economics Bulletin, 33, 2287-2297.
- 10. Nawata, K. (2015) Robust Estimation Based on the Third-Moment Restriction of the Error Terms for the Box-Cox Transformation Model: An Estimator Consistent under Heteroscedasticity. Economics Bulletin, 3, 1056-1064.
- 11. Hossain, M.Z. (2011) The Use of Box-Cox Transformation Technique in Economic and Statistical Analyses. Journal of Emerging Trends in Economics and Management Sciences, 2, 32-39.
- 12. Sakia, R.M. (1992) The Box-Cox Transformation Technique: A Review. The Statistician, 41, 169-178. http://dx.doi.org/10.2307/2348250
- 13. Amemiya, T. and Powell, J.L. (1981) A Comparison of the Box-Cox Maximum Likelihood Estimator and the Non- Linear Two Stage Least Squares Estimator. Journal of Econometrics, 17, 351-381. http://dx.doi.org/10.1016/0304-4076(81)90007-5
- 14. Yang, Z. (2006) A Modified Family of Power Transformations. Economics Letters, 92, 14-19. http://dx.doi.org/10.1016/j.econlet.2006.01.011
- 15. Yeo, I.K. and Johnson, R.A. (2000) A New Family of Power Transformation to Improve Normality or Symmetry. Biometrika, 87, 954-959. http://dx.doi.org/10.1093/biomet/87.4.954
- 16. Showalter, M.H. (1994) A Monte Carlo Investigation of the Box-Cox Model and a Nonlinear Least Squares Alternative. Review of Economics and Statistics, 76, 560-570. http://dx.doi.org/10.2307/2109980
- 17. Bickel, P.J. and Doksum, K.A. (1981) An Analysis of Transformations Revisited. Journal of American Statistical Association, 76, 296-311. http://dx.doi.org/10.1080/01621459.1981.10477649
- 18. Powell, J.L. (1996) Rescaled Method-of-Moments Estimation for the Box-Cox Regression Model. Economics Letters, 51, 259-265. http://dx.doi.org/10.1016/0165-1765(96)00811-7
- 19. Hausman, J. (1978) Specification Test in Econometrics. Econometrica, 46, 1251-1272. http://dx.doi.org/10.2307/1913827
- 20. Nawata, K. and McAleer, M. (2014) The Maximum Number of Parameters for the Hausman Test When the Estimators Are from Different Sets of Equations. Economic Letters, 123, 291-294. http://dx.doi.org/10.1016/j.econlet.2014.03.005
- 21. Nawata, K. and Kawabuchi, K. (2015) Financial Sustainability of the Japanese Medical Payment System: Analysis of the Japanese Medical Expenditure for Educational Hospitalization of Patients with Type 2 Diabetes. Health, 7, 1007- 1021. http://dx.doi.org/10.4236/health.2015.78118
NOTES
*How do we sustain the Japanese medical system?







