Open Journal of Applied Sciences
Vol.05 No.11(2015), Article ID:61248,8 pages
10.4236/ojapps.2015.511068
The Mixture of New Integral Transform and Homotopy Perturbation Method for Solving Discontinued Problems Arising in Nanotechnology
Kunjan Shah, Twinkle Singh
Applied Mathematics and Humanities Department, S. V. National Institute of Technology, Surat, India

Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 1 October 2015; accepted 16 November 2015; published 19 November 2015
ABSTRACT
In this paper, a reliable algorithm based on mixture of new integral transform and homotopy perturbation method is proposed to solve a nonlinear differential-difference equation arising in nanotechnology. Continuum hypothesis on nanoscales is invalid, and a differential-difference model is considered as an alternative approach to describing discontinued problems. The technique finds the solution without any discretization or restrictive assumptions and avoids the round-off errors. Comparison of the approximate solution with the exact one reveals that the method is very effective. It provides more realistic series solutions that converge very rapidly for nonlinear real physical problems.
Keywords:
New Integral Transform, Homotopy Perturbation Method, He’s Polynomials, Discretized mKDV Lattice Equation, Nanotechnology

1. Introduction
Non-linear phenomena that appear in many areas of scientific fields such as solid state physics, plasma physics, fluid mechanics, population models and chemical kinetics, can be modeled by nonlinear partial differential equations. In many different fields of science and engineering, it is important to obtain exact or numerical solution of the nonlinear partial differential equations. Searching of exact and numerical solution of nonlinear equations in science and engineering is still quite problematic that needs new methods for finding the exact and approximate solutions. Most of new nonlinear equations do not have a precise analytic solution; so, numerical methods have largely been used to handle these equations. There are also analytic techniques for nonlinear equations. Some of the classic analytic methods are Lyapunov’s artificial small parameter method [1] , d-expan- sion method [2] , perturbation techniques [3] [4] and Hirota bilinear method [5] [6] . In recent years, many research workers have paid attention to study the solutions of nonlinear partial differential equations by using various numerical methods. Among these are the Adomian decomposition method (ADM) [7] , He’s semi- inverse method [8] , the tanh method, the homotopy perturbation method (HPM), the sinh-cosh method, the differential transform method and the variational iteration method (VIM) [9] [10] .
According to E-infinity theory [11] - [13] , space at the quantum scale is not a continuum, and it is clear that nanotechnology possesses a considerable richness which bridges the gap between the discrete and the continuum [14] - [16] . On nanoscales, He et al. [17] found experimentally an uncertainty phenomenon similar to Heisen- berg’s uncertainty principle in quantum mechanics. Continuum hypothesis on the nanoscales becomes, therefore, invalid. He and Zhu [18] suggested some differential-difference models describing fascinating phenomena arising in heat/electron conduction and flow in carbon nanotubes, among which we will study the following model:
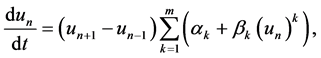 (1)
(1)
where 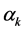 and
and 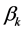 are constants. Physical interpretation is given in [18] . Equation (1) includes the well-known discretized mKdV lattice equation:
are constants. Physical interpretation is given in [18] . Equation (1) includes the well-known discretized mKdV lattice equation:
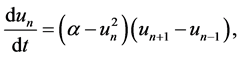 (2)
(2)
where the subscript n in Equation (1) represents the 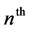 lattice. Previously such equations have been studied using the Exp-function method [19] - [21] , the variational iteration method [22] , homotopy perturbation method [23] , homotopy perturbation transform method [24] and the homotopy analysis method [25] .
lattice. Previously such equations have been studied using the Exp-function method [19] - [21] , the variational iteration method [22] , homotopy perturbation method [23] , homotopy perturbation transform method [24] and the homotopy analysis method [25] .
In this paper, we will study numerically Equation (2) using the mixture of new integral transform and homotopy perturbation method. It is worth mentioning that the proposed method is an elegant combination of the new integral transform, the homotopy perturbation method and He’s polynomials. The advantage of this technique is its capability of combining two powerful approaches for obtaining exact and approximate ana- lytical solutions for nonlinear equations. This method provides the solutions in terms of convergent series with easily computable components in a direct way without using linearization, perturbation or restrictive assumptions.
2. New Integral Transform
A new integral transform is derived from the classical Fourier integral. A new integral transform [26] was introduced by Artion Kashuri and Akli Fundo to facilitate the process of solving ordinary and partial differential equations in the time domain. Some integral transform methods such as Laplace, Fourier, Sumudu and Elzaki transforms methods, are used to solve general nonlinear non-homogenous partial differential equations with initial conditions and use fullness of these integral transform lies in their ability to transform differential equations into algebraic equations which allows simple and systematic solution procedures.
A new integral transform is defined for functions of exponential order. We consider functions in the set F defined as:
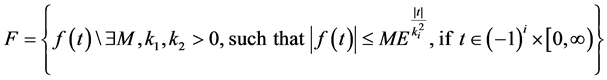 (3)
(3)
For a given function in the set F, the constant M must be finite number, 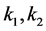 may be finite or infinite.
may be finite or infinite.
A new integral transform denoted by the operator 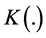 is defined by:
is defined by:
 (4)
(4)
For further detail and properties of this transform, see [26] - [28] .
3. Basic Idea of Mixture of New Integral Transform and Homotopy Perturbation Method
To illustrate the basic idea of this method, we consider a general nonlinear partial differential equation with the initial conditions of the form:
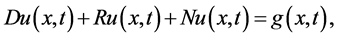 (5)
(5)
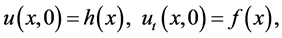 (6)
(6)
where D is the second order linear differential operator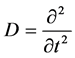 , R is the linear differential operator of less order than D, N represents the general nonlinear differential operator and
, R is the linear differential operator of less order than D, N represents the general nonlinear differential operator and 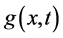 is the source term.
is the source term.
Taking the new integral transform on both sides of Equation (5), we get
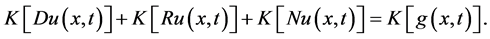 (7)
(7)
Using the differentiation property of new integral transform and above initial conditions (see Appendix), we have
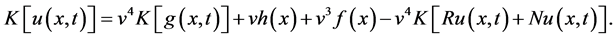 (8)
(8)
Now, applying new integral transform on both sides of Equation (8), we get

where 
According to homotopy perturbation method, we have [27]

Now, by substituting

and

for some He’s polynomials 

in Equation (10), we get

which is the mixture of the new integral transform and the homotopy perturbation method using He’s polyno- mials. Comparing the coefficient of like powers of p, the following approximations are obtained.
Then the solution is:

4. Application
In this section, we apply the mixture of new integral transform and homotopy perturbation method to solve (2), subject to the initial condition

where d is an arbitrary constant.
Applying the new integral transform on both sides of (2) subject to initial condition (16), we have

The inverse new integral transform implies that

Applying the homotopy perturbation method, we get

where 

Comparing the coefficients of like powers of p, we have
Therefore the approximate solution is

5. Numerical Result and Discussion
In this section, we calculate the numerical results of 


Figure 1. Comparison between mixture of new integral transform (- - -, blue) and exact solution (---, red).
Table 1. The results of the mixture of new integral transform homotopy perturbation method and the exact solution, when 

6. Conclusion
In this paper, we have successfully proposed the mixture of new integral transform and homotopy perturbation method for solving discontinued problems arising in nanotechnology. The result shows that the given method is a powerful and efficient technique in finding exact and approximate solutions for nonlinear differential equa- tions. Also, it can be observed that there is good agreement between the results obtained using the present method and the exact solution. It is worth mentioning that the method is capable of reducing the volume of the computational work as compared to the classical methods while still maintaining the high accuracy of the numerical result; the size reduction amounts to an improvement of the performance of the approach.
Cite this paper
Kunjan Shah,Twinkle Singh, (2015) The Mixture of New Integral Transform and Homotopy Perturbation Method for Solving Discontinued Problems Arising in Nanotechnology. Open Journal of Applied Sciences,05,688-695. doi: 10.4236/ojapps.2015.511068
References
- 1. Lyapunov, A.M. (1992) The General Problem of the Stability of Motion. International Journal of Control, 55, 531-534. http://dx.doi.org/10.1080/00207179208934253
- 2. Karmishin, A.V., Zhukov, A.I. and Kolosov, V.G. (1990) Methods of Dynamics Calculation and Testing for Thin- Walled Structures. Mashinostroyenie, Moscow.
- 3. He, J.H. (1999) Homotopy Perturbation Technique. Computer Methods in Applied Mechanics and Engineering, 178, 257-262. http://dx.doi.org/10.1016/S0045-7825(99)00018-3
- 4. Saberi-Nadjafi, J. and Ghorbani, A. (2009) He’s Homotopy Perturbation Method: An Effective Tool for Solving Nonlinear Integral and Integro Differential Equations. Computers & Mathematics with Applications, 58, 1354-1351. http://dx.doi.org/10.1016/j.camwa.2009.03.032
- 5. Hirota, R. (1971) Exact Solutions of the Korteweg-De Vries Equation for Multiple Collisions of Solitons. Physical Review Letters, 27, 1192-1194. http://dx.doi.org/10.1103/PhysRevLett.27.1192
- 6. Wazwaz, A.M. (2010) On Multiple Soliton Solutions for Coupled KdV-mkdV Equation. Nonlinear Science Letters A, 1, 289-296.
- 7. Adomian, G. (1994) Solving Frontier Problems of Physics: The Decomposition Method. Kluwer Academic Publication, Boston. http://dx.doi.org/10.1007/978-94-015-8289-6
- 8. Wu, G.C. and He, J.H. (2010) Fractional Calculus of Variations in Fractal Spacetime. Nonlinear Science Letters A, 1, 281-287.
- 9. He, J.H. (1999) Variational Iteration Method—A Kind of Nonlinear Analytical Technique: Some Examples. International Journal of Nonlinear Mechanics, 34, 699-708. http://dx.doi.org/10.1016/S0020-7462(98)00048-1
- 10. He, J.H. and Wu, X.H. (2007) Variational Iteration Method: New Development and Applications. Computers & Mathematics with Applications, 54, 881-894. http://dx.doi.org/10.1016/j.camwa.2006.12.083
- 11. El Naschie, M.S. (2007) Deterministic Quantum Mechanics versus Classical Mechanical Indeterminism. International Journal of Nonlinear Sciences and Numerical Simulation, 8, 5-10. http://dx.doi.org/10.1515/IJNSNS.2007.8.1.5
- 12. El Naschie, M.S. (2007) A Review of Applications and Results of E-Infinity Theory. International Journal of Nonlinear Sciences and Numerical Simulation, 8, 28-56.
- 13. El Naschie, M.S. (2007) Probability Set Particles. International Journal of Nonlinear Sciences and Numerical Simulation, 8, 117-119. http://dx.doi.org/10.1515/IJNSNS.2007.8.1.117
- 14. El Naschie, M.S. (2009) Nanotechnology for the Developing World. Chaos, Solitons & Fractals, 30, 769-773. http://dx.doi.org/10.1016/j.chaos.2006.04.037
- 15. Liu, Y. and He, J.H. (2007) Bubble Electrospinning for Mass Production of Nanofibers. International Journal of Nonlinear Sciences and Numerical Simulation, 8, 393-396. http://dx.doi.org/10.1515/ijnsns.2007.8.3.393
- 16. He, J.H., Wan, Y.Q. and Xu, L. (2007) Nano-Effects, Quantum-Like Properties in Electrospun Nanofibers. Chaos, Solitons & Fractals, 33, 26-37. http://dx.doi.org/10.1016/j.chaos.2006.09.023
- 17. He, J.H., Liu, Y.Y. and Xu, L. (2007) Micro Sphere with Nanoporosity by Electrospinning. Chaos, Solitons & Fractals, 32, 1096-1100. http://dx.doi.org/10.1016/j.chaos.2006.07.045
- 18. He, J.H. and Zhu, S.D. (2008) Differential-Difference Model for Nanotechnology. Journal of Physics: Conference Series, 96, Article ID: 012189. http://dx.doi.org/10.1088/1742-6596/96/1/012189
- 19. Zhu, S.D. (2007) Exp-Function Method for the Hybrid-Lattice System. International Journal of Nonlinear Sciences and Numerical Simulation, 8, 461-464. http://dx.doi.org/10.1515/ijnsns.2007.8.3.461
- 20. Zhu, S.D. (2007) Exp-Function Method for the Discrete mKdV Lattice. International Journal of Nonlinear Sciences and Numerical Simulation, 8, 465-469. http://dx.doi.org/10.1515/ijnsns.2007.8.3.465
- 21. Zhu, S.D. (2008) Discrete (2+1)-Dimensional Toda Lattice Equation via Exp-Function Method. Physics Letters A, 372, 654-657. http://dx.doi.org/10.1016/j.physleta.2007.07.085
- 22. Mokhtari, R. (2008) Variational Iteration Method for Solving Nonlinear Differential-Difference Equations. International Journal of Nonlinear Sciences and Numerical Simulation, 9, 19-24. http://dx.doi.org/10.1515/IJNSNS.2008.9.1.19
- 23. Zhu, S.D., Chu, Y.M. and Qiu, S.L. (2009) The Homotopy Perturbation Method for Discontinued Problems Arising in Nanotechnology. Computers and Mathematics with Applications, 58, 2398-2401. http://dx.doi.org/10.1016/j.camwa.2009.03.048
- 24. Singh, J., Kumar, D. and Kumar, S. (2013) A Reliable Algorithm for Solving Discontinued Problems Arising in Nanotechnology. Scientia Iranica, 20, 1059-1062.
- 25. Nik, H.S. and Golchaman, M. (2011) The Homotopy Analysis Method for Solving Discontinued Problems Arising in Nanotechnology. World Academy of Science, Engineering and Technology, 76, 891-894.
- 26. Kashuri, A. and Fundo, A. (2013) A New Integral Transform. Advances in Theoretical and Applied Mathematics, 8, 27-43.
- 27. Kashuri, A., Fundo, A. and Kreku, M. (2013) Mixture of a New Integral Transform and Homotopy Perturbation Method for Solving Nonlinear Partial Differential Equations. Advances in Pure Mathematics, 3, 317-323. http://dx.doi.org/10.4236/apm.2013.33045
- 28. Shah, K. and Singh, T. (2015) A Solution of the Burger’s Equation Arising in the Longitudinal Dispersion Phenomenon in Fluid Flow through Porous Media by Mixture of New Integral Transform and Homotopy Perturbation Method. Journal of Geoscience and Environment Protection, 3, 24-30. http://dx.doi.org/10.4236/gep.2015.34004
- 29. Ghorbani, A. (2009) Beyond Adomian’s Polynomials: He Polynomials. Chaos, Solitons & Fractals, 39, 1486-1492. http://dx.doi.org/10.1016/j.chaos.2007.06.034
- 30. Mohyud-Din, S.T., Noor, M.A. and Noor, K.I. (2009) Traveling Wave Solutions of Seventh-Order Generalized KdV Equation Using He’s Polynomials. International Journal of Nonlinear Sciences and Numerical Simulation, 10, 227- 233. http://dx.doi.org/10.1515/IJNSNS.2009.10.2.227
Appendix
Table A1. Fundamental properties of a new integral transform of partial derivatives.







