Received 6 July 2015; accepted 9 August 2015; published 12 August 2015

ABSTRACT

The penalty equation of LCP is transformed into the absolute value equation, and then the existence of solutions for the penalty equation is proved by the regularity of the interval matrix. We propose a generalized Newton method for solving the linear complementarity problem with the regular interval matrix based on the nonlinear penalized equation. Further, we prove that this method is convergent. Numerical experiments are presented to show that the generalized Newton method is effective.

Keywords:

Linear Complementarity Problem, Nonlinear Penalized Equation, Interval Matrix, Generalized Newton Method

1. Introduction

The linear complementarity problem, denoted by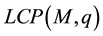, is to find a vector such that

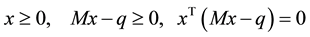(1.1)

where 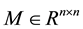is a given matrix and 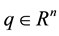is a given vector. This problem serves as a unified formulation of linear and quadratic programming problems as well as of two-person (noncooperative) matrix-games, and has several important applications in economics and engineering sciences; see Cottle, Pang, and Stone [1] and its references.

There exist several methods for solving, such as projection method, multi splitting method, interior point method, and the nonsmooth Newton method, smoothing Newton method, homotopy method etc. See [1] - [6] and its references.

In [7] , it given a nonlinear penalized Equation (1.2) corresponding to linear complementarity problem (1.1).

Find 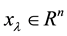such that

(1.2)

where 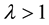is the penalized parameter, 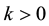, 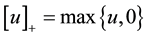and 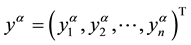for any .

The nonlinear penalized problems (1.2) corresponding to the linear complementarity problem (1.1), which its research has achieved good results. In 1984, Glowinski [1] studied nonlinear penalized Equation (1.2) in, and proved the convergence of penalized equation that matrix was symmetric positive definite. In 2006, Wang et al. [8] presented a power penalty function approach to the linear complementarity problem arising from pricing American options. It is shown that the solution to the penalized equation converges to that of the linear complementarity problem with matrix is positive definite. In 2008, Yang [7] proved that solution to this penalized Equations (1.2) converged to that of the LCP at an exponential rate for a positive definite matrix case where the diagonal entries were positive and off-diagonal entries were not greater than zero. The same year, Wang and Huang [9] presented a penalty method for solving a complementarity problem involving a second- order nonlinear parabolic differential operator, and defined a nonlinear parabolic partial differential equation (PDE) approximating the variational inequality using a power penalty term with a penalty constant, a power parameter k >0 and a smoothing parameter. And prove that the solution to the penalized PDE converges to that of the variational inequality in an appropriate norm at an arbitrary exponential rate of the form. Under some assumptions, Li [10] [11] proved that the solution to this equation converges to that of the linear complementarity problem with is a strict row diagonally dominant upper triangular P-matrix when the penalty parameter approaches to infinity and the convergence rate was also exponential. It is worth mentioning that the penalty technique has been widely used solving nonlinear programming, but it seems that there is a limited study for the LCP.

Although the studies solving for the linear complementarity problem based on the nonlinear penalized equation have good results. But there is no method that is given for solving the nonlinear penalized equation. Throughout the paper, we propose a generalized Newton method for solving the nonlinear penalized equation with under the suppose is regular. So the method can better to solve linear complementarity problem. We will show that the proposed method is convergent. Numerical experiments are also given to show the effectiveness of the proposed method.

2. Preliminaries

Some words about our notation: refers to the identity matrix, and represents the 2-norm. For, all vectors are column vectors, refers to the transpose of the, , that generalized Jacobian, where denotes diagonal matrix, On the diagonal elements with component 1.0 or corresponding to the component of which is positive , negative or zero, respectively.

The definition of interval matrix arises from the linear interval equations [12] , given two matrices and, an interval matrix, where refers to for each. is called regular if each is nonsingular.

Lemma 1: Assume that interval matrix is regular. Then for diagonal matrix and real number, is nonsingular.

Proof: By definition of, for every x, we have then

By the assumptions, we have is nonsingular. □

Lemma 2: Let. Then

Definition 1 [1] : A matrix is said to be a P-matrix if all its principal minors are positive.

Lemma 3 [1] : A matrix is a P-matrix if and only if the has a unique solution for all vectors.

3. Generalized Newton Method

In this section, we will propose that a new generalized Newton method based on the nonlinear penalized equation for solving the linear complementarity problem. Because when, penalty term of the nonlinear penalized equation (1.2) is none Lipschitz continuously, hence we only discusses a case that. So from nonlinear penalized equation (1.2), we have that

(3.1)

These case penalty problems for the continuous Variational Inequality and the linear complementarity problems are discussed in [2] [13] .

Let us note

(3.2)

Thus, nonlinear penalized equation (3.1) is equivalent to the equation.

A generalized Jacobian of is given by

where is a diagonal matrix whose diagonal entries are equal 1,0 or a real number

depending on whether the corresponding component of is positive, negative, or zero. The generalized Newton method for finding a solution of the equation consists of the following iteration:

(3.3)

Then

Since, consequently

(3.4)

Proposition 1 equivalent to, where

Proof: Since, then, we have

By [14] , its equivalent to

(3.5)

Let then. □

Proposition 2 has a unique solution if and only if the interval matrix is regular.

Proof: Since, by theorem 1.2 of [12] , if is regular, then is P-matrix, which implies that the LCP has a unique solution for any [1] , from the re-

lation between the (3.1) and the LCP (3.5), we can easily deduce that the (3.1) is uniquely solvable for any. □

Algorithm 3

Step 1: Choose an arbitrary initial point, and given, , , let;

Step 2: for the, computer by solving

(3.6)

Step 3: If, let go to step 4. Otherwise, go to step 2.

Step4: If and, terminate, is solution of LCP. Otherwise let, let, go to 2.

4. The Convergence of the Algorithm

We will show that the sequence generated by the generalized Newton iteration (3.6) converges to an accumulation point associated with. First, we establish boundness of the sequence for any generated by the Newton iterates (3.6) and hence the existence of accumulation point at each generalized Newton iteration.

Theorem 3: Suppose that the interval matrix is regular. Then, the sequence generated by Algorithm 3 is bounded. Consequently, there exits an accumulation points such that .

Proof: Suppose that sequence is unbounded, Thus, there exists an infinite nonzero subsequence such that

where is main diagonal element of diagonal matrix which is.

We know subsequence is bounded. Hence, exists convergence subsequence and assume that convergence point is, and satisfy

Letting yields

Since and the interval matrix is regular, we know that is exists and hence, contradicting to the fact that. Consequently, the sequence is bounded and there exists an accumulation point of such that

□

Under a somewhat restrictive assumption we can establish finite termination of the generalized Newton iteration at a penalized equation solution as follows.

Theorem 4: Suppose that the interval matrix is regular and holds for all sufficiently large, then the generalized Newton iteration (3.6) linearly converges from any starting point to a solution of the nonlinear penalized equation (3.1).

Proof: Suppose that is a solution of nonlinear penalized equation. By the lemma 1, is nonsingular. To simply notation, let, and since, have, , hence

since and by the lemma 2, we have

(4.2)

Letting and taking limits in both sides of the last inequality above, we have

So the iteration (3.6) linearly converges to a solution of nonlinear penalized equation (3.1). □

In here, we will focus on the convergence of Algorithm 3.

Theorem 5: Suppose M is P-Matrix and that the interval matrix is regular and holds, then Algorithm 3 linearly converges from any starting point to a solution of the (1.1).

Proof: Since M is P-Matrix, then the has a unique solution, let the solution denote, by the assumptions of the theorem, the generalized Newton iteration (3.6) linearly converges to a solution of the nonlinear penalized equation (3.1).

let, then

we have □

5. Numerical Experiments

In this section, we give some numerical results in order to show the practical performance of Algorithm 2.1. Numerical results were obtained by using Matlab R2007 (b) on a 1G RAM, 1.86 Ghz Intel Core 2 processor. Throughout the computational experiments, the parameters were set as, ,.

Example 1: The matrix of linear complementarity problem of as follows (This example appear in the Geiger and Kanzow [15] , Jiang and Qi [16] , YONG Long-quan, DENG Fang-an, CHEN Tao [17] ):

The computational results are shown in Table 1. This is initial point, is number of inner iterations, the outer iteration number is, is iteration results.

Example 2: The matrix of linear complementarity problem of as follows (This example appear in the Geiger and Kanzow [15] , Jiang and Qi [16] , YONG Long-quan, DENG Fang-an, CHEN Tao [17] ):

The computational results are shown in Table 2. This is initial point, is number of inner iterations, the outer iteration number is, is iteration results.

Supported

This work supported by the Science Foundation of Inner Mongolia in China (2011MS0114)

Cite this paper

Hai-ShanHan,Lan-Ying , (2015) An Interval Matrix Based Generalized Newton Method for Linear Complementarity Problems. Open Journal of Applied Sciences,05,443-449. doi: 10.4236/ojapps.2015.58044

References