Open Journal of Applied Sciences
Vol.05 No.07(2015), Article ID:57975,10 pages
10.4236/ojapps.2015.57035
Long Term Soil and Water Assessment Tool (SWAT) Calibration from an Ecohydrology Perspective
Sivarajah Mylevaganam1*, Raghavan Srinivasan1, Vijay P. Singh2
1Spatial Sciences Laboratory, Texas A & M University, College Station, TX, USA
2Department of Biological and Agricultural Engineering, Texas A & M University, College Station, TX, USA
Email: *sivaloga@hushmail.com
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 14 June 2015; accepted 12 July 2015; published 15 July 2015
ABSTRACT
The performance on prediction by mathematical models which represent the conceived image of a system such as hydrology is oftentimes represented through calibration and verification pro- cesses. Oftentimes a best fit between observed and predicted flows is obtained through correlation coefficient (R2) and the Nash Sutcliffe model efficiency (NSE) by minimizing the average Root Mean Square Error (RMSE) of the observed versus simulated flows. However, these days, a new paradigm is emerging wherein accounting for the flow variability for the protection of freshwater biodiversity and maintenance of goods and services that rivers provide is paramount. Therefore, from an ecohydrology perspective, it is not clear if the existing method of model calibration meets the needs of the riverine ecosystem at its best. Thus, this study investigates and proposes a methodology using entropy theory to gage the calibration of Soil and Water Assessment Tool (SWAT) from an ecohydrology perspective characterized by the natural flow-regime paradigm: Indicators of Hydrologic Alteration.
Keywords:
Principle of Maximum Entropy, Ecohydrology, Indicators of Hydrologic Alteration, Maximum Entropy Ordered Weighted Averaging, Soil and Water Assessment Tool, Calibration

1. Introduction
Mathematical models of watershed hydrology are employed to simulate the effects of various conservation programs and to determine suitable conservation programs for given watersheds and agronomic settings [1] . Soil and Water Assessment Tool (SWAT) is such model. SWAT is a basin-scale, continuous-time model and operates on a daily time step [2] . SWAT has been developed to quantify the impact of land use and management on water, sediment, and agricultural chemical yields from ungauged watersheds. The model is validated by the agreement between observed and predicted flows, using parameter values obtained by calibration.
Model calibration is the process of estimating model parameters by comparing model predictions for a given set of assumed conditions with observed data for the same conditions [3] . A number of studies have addressed model evaluation statistics [4] . Borah and Bera [5] present an excellent review of values for various statistics used in hydrologic and nonpoint-source model applications. More importantly, [1] provides guidance on acceptable ranges of values for each statistic. By far the most widely used statistics reported for hydrologic calibration are the correlation coefficient (R2) and the Nash Sutcliffe model efficiency (NSE) coefficient. The R2 value measures how well the simulated versus observed regression line approaches an ideal match and ranges from 0 to 1, with a value of 0 indicating no correlation and a value of 1 representing that the predicted dispersion equals the measured dispersion [1] [6] . The NSE ranges from −∞ to 1 and measures how well the simulated versus observed data matches the 1:1 line whose slope is equal to 1.
However, there is now a broad acceptance that it is in society’s best interests to recognize that rivers and adjacent wetlands need adequate water to sustain ecological processes and associated goods and services [7] [8] . The flow variability is important to the health of riverine ecosystems. They have to be varied at different times of the year to keep the ecosystem in good working order by mimicking the natural variability being seen in river flows. Low flows, for example, trigger migration and reproduction within different animal species. On the other hand, high flows, for example, help some riverside plants to reproduce and also ensure that river channels keep their shapes and do not silt up [9] [10] . Therefore, it is now recognized that the full range of natural intra- and inter-annual variation of hydrological regimes and associated characteristics of timing, duration, frequency and rate of change, as shown in Table 1, are critical to sustain the full native biodiversity and integrity of riverine ecosystems (the “natural flow-regime paradigm”: Indicators of Hydrologic Alteration (IHA) [9] -[11] ).
Therefore, performing the calibration process just by looking at the above discussed statistical measures of observed versus predicted flows may not portray how well the predicted system will meet the need of the riverine ecosystem that is defined as a function of temporal variations in river flows. Getting a best fit between observed and predicted flows through NSE or R2 by minimizing the average Root Mean Square Error (RMSE) of the observed versus simulated flows may lose the vital core needed to sustain the riverine ecosystem.
Moreover, in SWAT and in contemporary hydrological models, to capture the spatial variability, the watershed is subdivided into few subwatersheds/subbasins. The modeler can define as many or as few subwatersheds as desired according to the critical source area (CSA), the threshold at which stream network appears. This has been exercised as a trial and error process. Presently, there are no standard protocols for deciding what scheme to adopt to capture the spatial variability through subwatersheds. Each subwatershed is then further di-
Table 1. Summary of Hydrological Parameters Used in IHA [11] .
vided into a number of hydrologic representative units (HRU) based on unique combinations of land use and land cover (LULC), and soil types within the subwatershed. To simplify the hydrological system further, an HRU threshold is applied to remove smaller HRUs.
However, the question is whether these conventional calibrated flows at the selected spatial scales (i.e., CSA and HRU threshold) best represent the need of the riverine ecosystem that is characterized through IHA. Furthermore, which one of the considered scales has to be considered as the best model that best represent the need of the riverine ecosystem. It is also worth mentioning that such calibrated models are employed subsequently to analyze the water management scenarios to reflect the real nature. Thus, will these calibrated models mimic the nature that’s being observed at the gage location subsequently at subwatershed scale from an ecohydrology perspective? Therefore, there has to be a way to gage this to ensure that the best calibrated model reflects the need of the riverine system at its best. In other words, there has to be a way to gage the alteration on the need of the riverine system caused by the best calibrated model. Thus, it is the objective of this study to investigate the SWAT calibration at different spatial scales from an ecohydrology perspective characterized by the natural flow-regime paradigm: Indicators of Hydrologic Alteration.
2. Soil and Water Assessment Tool (SWAT)
SWAT is a river basin or watershed scale model developed by the United States Department of Agriculture(USDA)―Agricultural Research Service(ARS) to predict the impact of land-management practices on water, sediment and agricultural chemical yields in large complex watersheds with varying soils, land use and management conditions over long periods of time [2] . SWAT operates on daily time step and predicts water quality and quantity at the subwatershed level. The watershed is defined by the main watershed outlet as chosen by the user. To capture the spatial variability, the watershed is then subdivided into subwatersheds/subbasins. The modeler can define as many or as few subwatersheds as desired according to the CSA, the threshold at which stream network appears. This has been exercised as a trial and error process. Presently, there are no standard protocols for deciding what scheme to adopt to capture the spatial variability through subwatersheds. Each subwatershed is then further divided into a number of HRUs based on unique combinations of LULC, and soil types within the subwatershed. To simplify the hydrological system further, an HRU threshold is applied to remove smaller HRUs. However, these HRUs are not spatially defined within the subwatershed. They are simply accounting categories which represent the total area of the unique LULC, and soil type they represent within a subwatershed. A subwatershed contains at least one HRU, a tributary channel and a main channel or reach. Loads from the subwatershed enter the channel network in the associated reach segment. HRU-scale processes are simulated separately for each HRU and then aggregated up to the subwatershed scale and then routed through the stream system. Details of SWAT are presented by [2] .
3. Study Area
The study area is Kings Creek, a tributary of the Cedar Creek River basin, Texas (Figure 1). It has a drainage area of 614 km2 as delineated from a USGS streamflow gaging station (32.513˚N, 96.3286˚W). Its elevation ranges from 107 m to 190 m and its land use is mainly hay (34%) and range (34.5%). The remaining areas were composed of agricultural, forest-deciduous, etc. The average annual precipitation in the study area is 975 mm.
4. Methodology and Discussion of Results
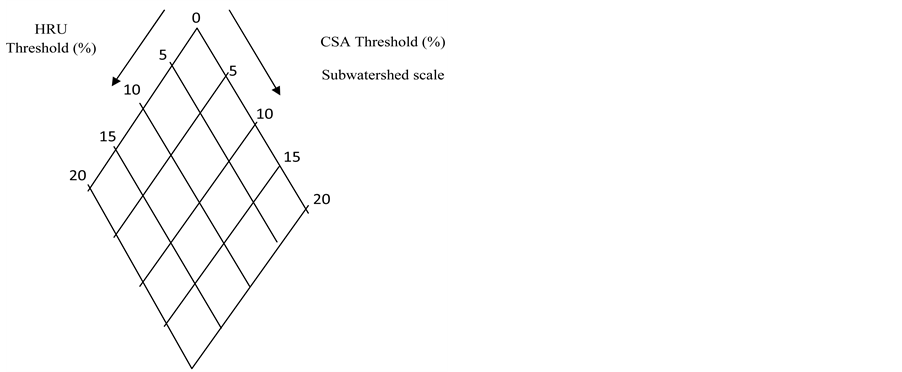
Input data on topography were extracted from a digital elevation model (DEM). The 30 m DEM used in delineating the watersheds was taken from the NHDPlus dataset, an integrated suite of application-ready geospatial data products envisioned by the U.S. Environmental Protection Agency. Soil dataset was obtained from the USDA-NRCS State Soil Geographic Data Base (STATSGO). Digital land use/land cover data for the Kings Creek watershed was obtained from the National Land Cover Dataset (NLCD). The observed daily streamflow data used for calibrating SWAT was obtained from the USGS National Water Information System (NWIS). The study area was set up to run on a daily time step. As shown in Figure 2, as presently there are no standard protocols for deciding what scheme to adopt to capture the spatial variability through subwatersheds and HRUs, SWAT was run for a particular combination of CSA and HRU threshold.
The percentile of subwatershed scale was obtained by considering the lower most CSA (1000ha) as the 0%
Figure 1. Kings Creek, a Tributary of the Cedar Creek River Basin, Texas.
Figure 2. Spatial Scale in SWAT.
and the upper most CSA (5000 ha) as the 20%. The percentile of HRU scale was obtained by considering an equal threshold on landuse and soil. In other words, a 5% HRU scale represents a 5% landuse and 5% soil. Surface runoff was calculated using the Soil Conservation Service (SCS) curve number method. The Penman- Monteith method was used to determine potential evapotranspiration. Channel water routing was performed using the Muskingum routing method.
4.1. Goodness of Fit Criteria
Manual and automatic calibration methods were combined for calibrating SWAT using the measured stream flow data at (32.513˚N, 96.3286˚W). For this analysis, twenty years, from 1 January 1963 to 31 December 1982, of meteorological and hydrometric flow data were utilized, including two years of “warm-up” period. The objective function was to minimize the RMSE of observed versus simulated flows. RMSE was defined as:
 (1)
(1)
where n is the number of time steps, Qobs,i is the observed streamflow at time i, and Qsim,i is the simulated streamflow at time i. The NSE was used to evaluate SWAT’s overall performance at calibration and validation. The NSE was defined as:
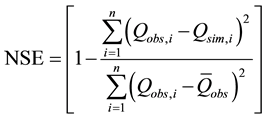 (2)
(2)
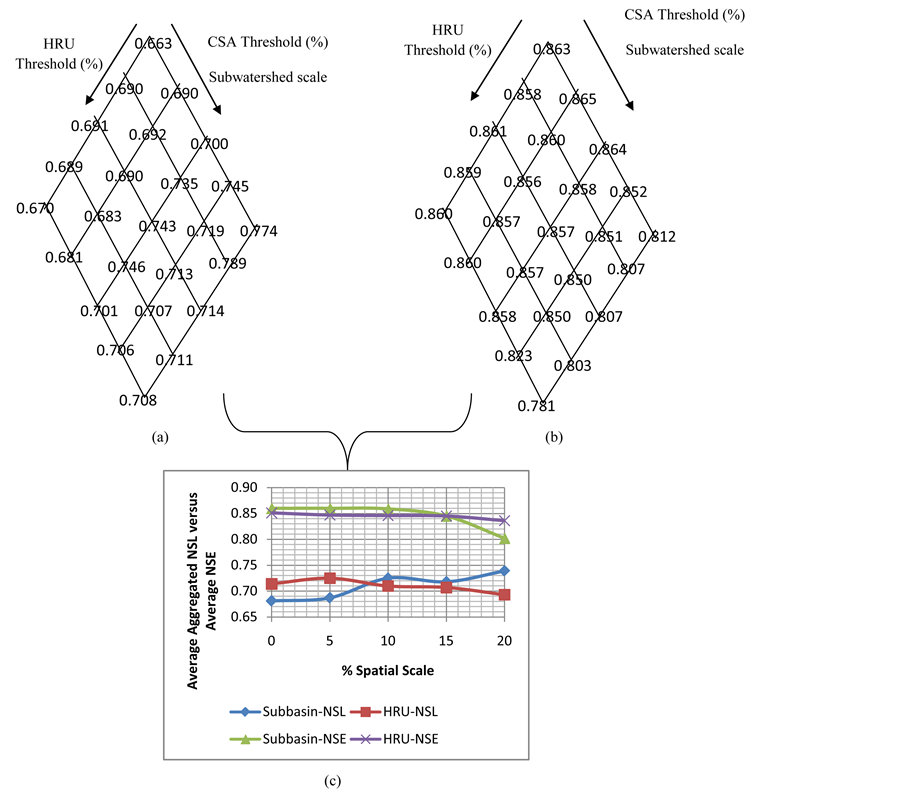
The following parameters were tuned during the calibration process: Curve Number (CN), Soil Available Water Capacity (SOIL_AWC), Soil Evaporation Coefficient (ESCO), Base-Flow Alpha Factor (ALPHA_BF), and Groundwater Revap. Coefficient (GW_REVAP). The model validation was done using the calibrated parameters. The model validation involved re-running the model using input data different from the data used in calibration. Four years of observed flow data from 01 January 1983 to 31 December, 1986, were used to validate the model. Figure 3(a) shows the NSE for monthly stream flows during the calibration for different combinations of CSA and HRU threshold as presented in Figure 2.
Among the considered spatial scales, 5% of subwatershed scale and 0% of HRU scale produced the best NSE value of 0.865 and 0.823 for the study area during the calibration and validation, respectively. Whereas 20% of subwatershed scale and 20% of HRU scale produced the lower most NSE of 0.781 and 0.727 during the calibration and validation respectively. Although the variation of NSE among the considered spatial scales was not that significant, the altered level of NSE, which is the absolute deviation with respect to the highest NSE, was high with the increased HRU scale at the high subwatershed scale as highlighted in Figure 3(b).
4.2. Determination of Least-Biased Probability Distributions of IHA Parameters
Having calibrated and validated SWAT for the combination of CSA and HRU threshold as presented in Figure 2, it was hypothesized that each of the 32 biologically relevant hydrologic parameters, proposed by [11] , could be considered as a random variable. Then, for each of the parameters, the least biased probability distribution was obtained by maximizing the Shannon entropy [12] :
 (3)
(3)
in accord with the Principle of Maximum Entropy (POME), subject to known constraints. In Equation (3) E is the Shannon entropy,
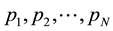 are the values of probabilities corresponding to the specific values
are the values of probabilities corresponding to the specific values
 of the biologically relevant hydrologic parameter X, and N is the number of values. These
of the biologically relevant hydrologic parameter X, and N is the number of values. These
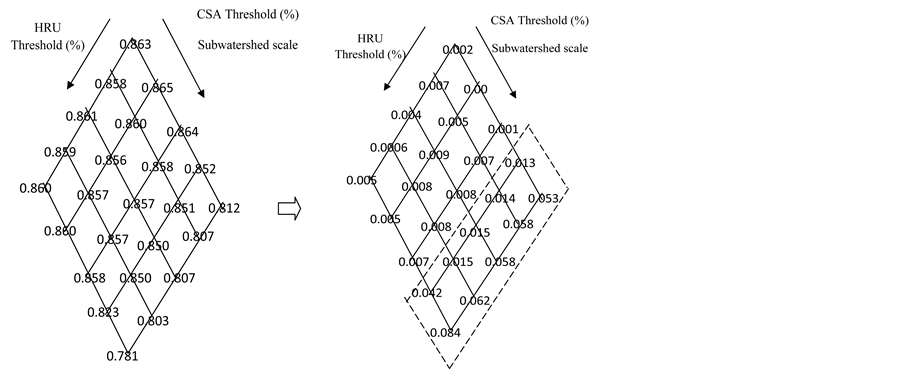
Figure 3. (a) SWAT Model Fit (NSE) for Monthly Stream Flows During the Calibration for Different Combinations of CSA and HRU Threshold; (b) The Altered Level of NSE(i.e., Absolute Deviation with Respect to the Highest NSE).
probabilities constitute the probability distribution
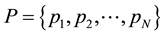 of the parameter
of the parameter
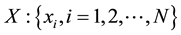 in question. For maximization, the constraints on X can be expressed in terms of averages or expected values of the parameter reflecting the state of the ecosystem as
in question. For maximization, the constraints on X can be expressed in terms of averages or expected values of the parameter reflecting the state of the ecosystem as
 (4)
(4)
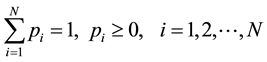 (5)
(5)
where Cj is the jth constraint, m is the number of constraints, and
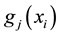 is the jth function of x. Using the method of Lagrange multipliers, the maximization of E would lead to the least biased P expressed as [12] :
is the jth function of x. Using the method of Lagrange multipliers, the maximization of E would lead to the least biased P expressed as [12] :
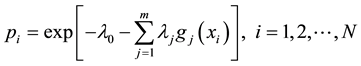 (6)
(6)
In practical applications, functions
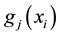 are expressed as simple moments and the number of constraint is kept to two or three. Thus, the first constraint would be the average and the second constraint would be the second moment or variance. Once the least biased probability distribution is determined using Equation (6), it is inserted in Equation (3) to obtain the maximum entropy. This process was carried out for each of the IHA parameters and for each spatial scale as shown in Figure 2.
are expressed as simple moments and the number of constraint is kept to two or three. Thus, the first constraint would be the average and the second constraint would be the second moment or variance. Once the least biased probability distribution is determined using Equation (6), it is inserted in Equation (3) to obtain the maximum entropy. This process was carried out for each of the IHA parameters and for each spatial scale as shown in Figure 2.
4.3. Computation of Deviation (Non-Satisfaction Level)
Non-Satisfaction Level (NSL) for an “nth” parameter was defined as
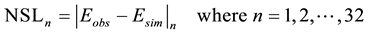
where

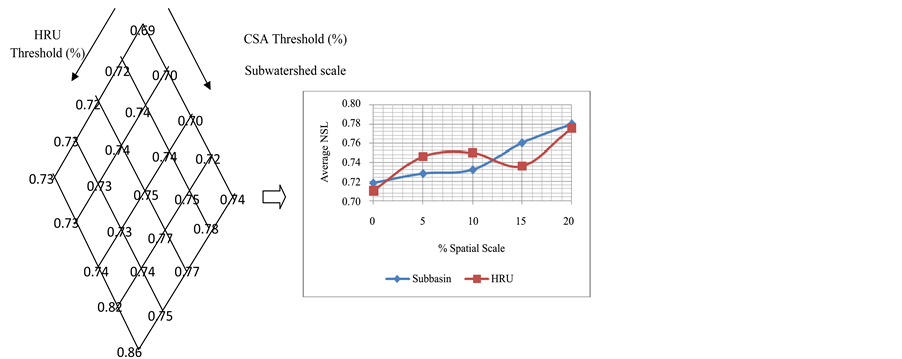
The computed values of average NSL for IHA group-1 which provides the general measure of habitat availability or suitability and an expression of environmental contingency [11] is shown in Figure 5. The value of the average NSL at the best spatial scale (i.e., 5% of CSA threshold and 0% of HRU threshold) which gave the highest NSE was relatively low compared to the others even though it did not yield the lowest average NSL. Furthermore, as the subwatershed threshold increased the alteration on IHA group-1 increased too.
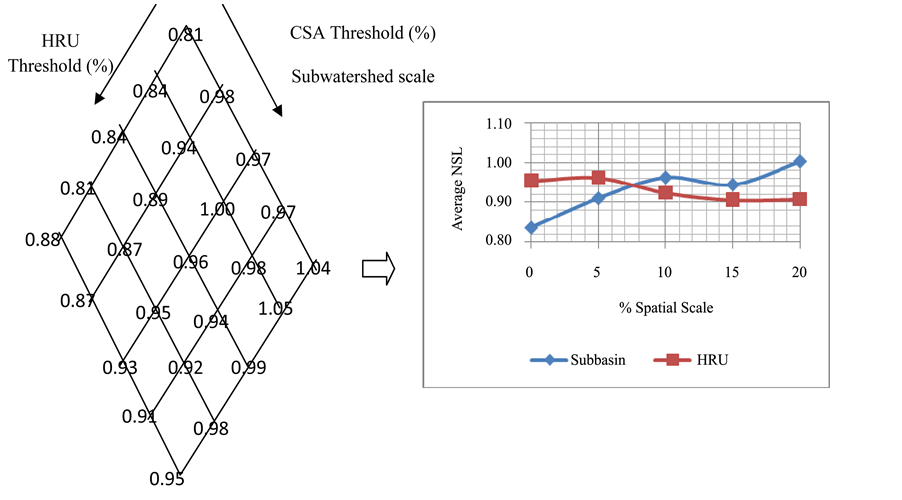
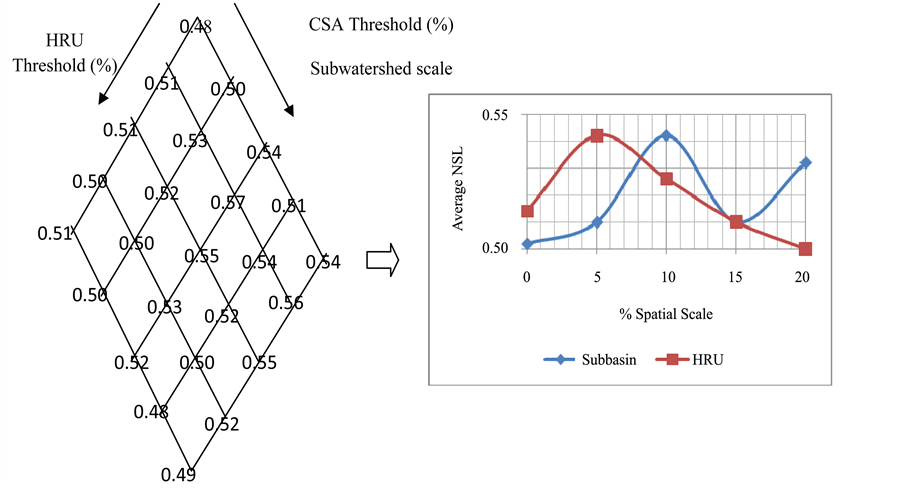
The average NSL for IHA group-2 which measures the structuring of river channel morphology, physical habitat conditions, and aquatic ecosystems by abiotic versus biotic factors [11] was relatively higher than the average NSL for IHA group-1 as shown in Figure 6. The average NSL at the best spatial scale (i.e., 5% of CSA threshold and 0% of HRU threshold) which gave the highest NSE was relatively high. Furthermore, the tendency of the model to reduce the impact on IHA group-2 increases as the HRU scale increases. This is in contrast to what was observed for the IHA group-1. As shown in Figure 7, the average NSL for IHA group-3 which measures the key life cycle phases [11] was lower than the average NSL for the IHA group-1 and IHA group-2.
However, it is reasonable to say that these NSLs of 32 parameters may have priorities among themselves. Some of the parameters may not be of important, even though they define the underlying riverine ecosystem. Thus, there has to be a way to consider this to reflect the overall status of the alteration on ecohydrology with the SWAT simulation, which could go in parallel with the NSE.
4.4. Aggregated Non-Satisfaction Level
The values of NSLs of biological parameters were aggregated based on [13] finding such that the final aggregation maximized the information associated with each biological parameter. The Ordered Weighted Averaging (OWA) operator introduced by [13] is a general type operator that provides flexibility in the aggregation process such that the aggregated value is bounded between minimum and maximum values of input parameters. The OWA operator is defined as
Figure 4. Evaluation of Non-Satisfaction Level.
Figure 5. Average NSL for IHA Group-1.

where the computed value of entropy for each of the 32 parameters is the argument (ai), bj is the jth largest of ai,
and wj are a collection of weights such that wj ?[0,1] and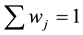
Figure 6. Average NSL for IHA Group-2.
Figure 7. Average NSL for IHA Group-3.

The methodology used for obtaining the OWA weighting vector was based on [13] . This approach, which only requires the specification of just the Orness value (1-Andness), generates a class of OWA weights that are called Maximum Entropy Operator Weighted Averaging (ME-OWA) weights. The determination of these weights
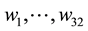
maximize:
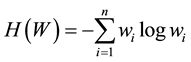
subject to:
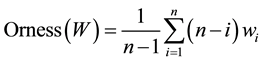

The Orness characterizes the degree to which the aggregation is like an “OR” operator. For the analysis an Orness value of 0.75 was assumed in this study to ensure that the impact of all the IHA parameters is considered in the index development and to avoid assigning equal weights as some of the parameters may have more influence on defining the underlying ecosystem. Then, an array of weights wj was generated using Equations (10) and (11).
As shown in Figure 8, the value of the aggregated NSL at the best spatial scale (i.e., 5% of CSA threshold
Figure 8. (a) Aggregated NSL for Different Combinations of CSA and HRU Threshold; (b) NSE for Different Combinations of CSA and HRU Threshold; (c) Average Aggregated NSL versus Average NSE.
and 0% of HRU threshold) which gave the highest NSE was relatively low even though it did not yield the lowest aggregated NSL. Furthermore, the lowest aggregated NSL was observed at 0% subwatershed scale and 0% HRU scale. In other words, the lowest aggregated NSL occurs with the hydrological system without any simplification on HRU. Moreover, the ability of the model to reflect the need of the riverine ecosystem tends to decrease as the subwatershed scale increased. This is justified with the average NSE that tends to decrease as the subwatershed scale increased.
5. Conclusions and Recommendations
This study shows how the conventional calibration process by minimizing the RMSE of the observed versus simulated flows of a hydrological model like SWAT can be gauged on its ability to retain the need of the riverine ecosystem characterized by the natural flow-regime paradigm: Indicators of Hydrologic Alteration. The outcome of this study shows the followings:
1) The ability of the calibrated model to reflect the need of the riverine ecosystem tends to decrease as the subwatershed scale (i.e., CSA threshold) increased.
2) The best calibrated model does not yield the best result for the selected study area from an ecohydrology perspective. However, the deviation is not that significant.
3) The model without any simplifications on HRU and CSA threshold gives the best result for the selected study area from an ecohydrology perspective.
4) The proposed methodology can be used as a surrogate when there is a tie to select the best simulation along with spatial scales.
Acknowledgements
The authors would like to thank Texas Water Resources Institute and U.S. Geological Survey for providing the financial support to conduct this research.
Cite this paper
SivarajahMylevaganam,RaghavanSrinivasan,Vijay P.Singh, (2015) Long Term Soil and Water Assessment Tool (SWAT) Calibration from an Ecohydrology Perspective. Open Journal of Applied Sciences,05,344-354. doi: 10.4236/ojapps.2015.57035
References
- 1. Moriasi, D.N., Arnold, J.G., Van Liew, M.W., Bingner, R.L., Harmel, R.D. and Veith, T.L. (2007) Model Evaluation Guidelines for Systematic Quantification of Accuracy in Watershed Simulations. Transactions of the ASABE, 50, 885- 900.
http://dx.doi.org/10.13031/2013.23153 - 2. Gassman, P.W., Reyes, M.R., Green, C.H. and Arnold, J.G. (2007) The Soil and Water Assessment Tool: Historical Development, Applications, and Future Research Directions. Transactions of the ASABE, 50, 1211-1250. http://dx.doi.org/10.13031/2013.23637
- 3. Balascio, C.C., Palmeri, D.J. and Gao H. (1998) Use of a Genetic Algorithm and Multi-Objective Programming for Ca- libration of a Hydrologic Model. Transactions of the ASAE, 41, 615-619. http://dx.doi.org/10.13031/2013.17229
- 4. Wang, X. and Melesse, A.M. (2005) Evaluation of the SWAT Model’S Snowmelt Hydrology in a Northwestern Minnesota Watershed. Transactions of the ASABE, 48, 1359-1376.
http://dx.doi.org/10.13031/2013.19194 - 5. Borah, D.K. and Bera, M. (2004) Watershed-Scale Hydrologic and Nonpoint-Source Pollution Models: Review of Applications. Transactions of the ASAE, 47, 789-803.
http://dx.doi.org/10.13031/2013.16110 - 6. Krause, P., Boyle, D.P. and Base, F. (2005) Comparison of Different Efficiency Criteria for Hydrological Model Assessment. Advances in Geosciences, 5, 89-97.
http://dx.doi.org/10.5194/adgeo-5-89-2005 - 7. Naiman, R.J., Bunn, S.E., Nilsson, C., Petts, G.E., Pinay, G. and Thompson, L.C. (2002) Legitimizing Fluvial Ecosystems as Users of Water: An Overview. Environmental Management, 30, 455-467. http://dx.doi.org/10.1007/s00267-002-2734-3
- 8. Postel, S. and Richter, B.D. (2003) Rivers for Life: Managing Water for People and Nature. Island Press, Washington DC.
- 9. Poff, N.L., Allan, J.D., Bain, M.B., Karr, J.R., Prestegaard, K.L., Richter, B.D., Sparks, R.E. and Stromberg, J.C. (1997) The Natural Flow Regime: A Paradigm for River Conservation and Restoration. BioScience, 47, 769-784. http://dx.doi.org/10.2307/1313099
- 10. Lytle, D.H. and Poff, N.L. (2004) Adaptation to Natural Flow Regimes. Trends in Ecology and Evolution, 19, 94-100. http://dx.doi.org/10.1016/j.tree.2003.10.002
- 11. Richter, B.D., Baumgartner, J.V., Powel, J. and Braun, D.P. (1996) A Method for Assessing Hydrologic Alteration within Ecosystems. Conservation Biology, 10, 1163-1174.
http://dx.doi.org/10.1046/j.1523-1739.1996.10041163.x - 12. Singh, V.P. (1998) The Use of Entropy in Hydrology and Water Resources. Hydrological Processes, 11, 587-626.
http://dx.doi.org/10.1002/(SICI)1099-1085(199705)11:6<587::AID-HYP479>3.0.CO;2-P - 13. Yager, R.R. (1999) Induced Ordered Weighted Averaging Operators. IEEE Transactions on Systems, Man and Cybernetics, 29, 141-150. http://dx.doi.org/10.1109/3477.752789
NOTES
*Corresponding author.