Open Journal of Applied Sciences
Vol.05 No.05(2015), Article ID:56298,7 pages
10.4236/ojapps.2015.55021
On Solution of the Problem of Bending of Orthotropic Plates on the Basis of Bimoment Theory
Makhamatali K. Usarov
Institute of Seismic Stability of Structures, Academy of Sciences of Uzbekistan, Tashkent, Uzbekistan
Email: umakhamatali@mail.ru
Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 15 April 2015; accepted 8 May 2015; published 13 May 2015
ABSTRACT
This paper is devoted to the development of new theory of orthotropic thick plates with account of internal forces, moments and bimoments. An equation of motion of plates is described by two systems with nine equations each. Boundary conditions depended on displacements, forces, moments and bimoments are given. An exact solution of the bending of thick plate under the effect of sine load is built. Numerical results for maximal values of displacements and stresses of the plate are obtained.
Keywords:
Plate, Orthotropy, Isotropy, Force, Moment, Bimoment, Equation of Motion, Exact Solution

1. Introduction
Specified theories of plates are widely used in analysis of structure elements. Review and general technique for constructing a specified theory can be found in [1] [2] . In spatial case of bending and vibrations along the thickness of the plate, the displacements vary according to nonlinear law, and classical theories of plates and shells become unacceptable. In general case the field of displacement of thick plates does not obey to any simplifying hypotheses. It is necessary to take into account all the components of the tensor of stress and strain: 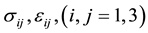 ; by them we will introduce tensile and crosscutting forces, bending and torsion moments and the concept of bimoments [3] , generated due to nonlinear law of distribution of displacements in cross-sections of the plate.
; by them we will introduce tensile and crosscutting forces, bending and torsion moments and the concept of bimoments [3] , generated due to nonlinear law of distribution of displacements in cross-sections of the plate.
This article briefly describes a method of constructing a theory of plates with bimoments. Determinant correlations of forces, moments, bimoments and the equations of motion in relation to these types of force factors are given.
2. Statement of the Problem
Consider orthotropic thick plate of constant thickness 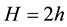 and dimensions
and dimensions 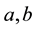 in plan. Introduce the signs:
in plan. Introduce the signs: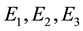 ―elasticity modulus and
―elasticity modulus and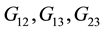 ―shear modulus;
―shear modulus;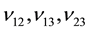 ―Poisson’s ratio of plate material.
―Poisson’s ratio of plate material.
Introduce Cartesian system of coordinates 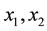 and z. Axis
and z. Axis 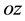 is directed vertically downwards. Let distributed surface normal and tangential loads are applied to the lower and the upper face surfaces of the plate
is directed vertically downwards. Let distributed surface normal and tangential loads are applied to the lower and the upper face surfaces of the plate
 and
and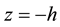 . Normal loads in
. Normal loads in 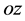 axis we will designate as
axis we will designate as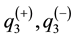 , tangential loads in direction
, tangential loads in direction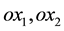 ?
?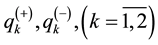 . Vlasov B. F. [4] has built an exact analytical solution of this problem in trigono-
. Vlasov B. F. [4] has built an exact analytical solution of this problem in trigono-
metric series.
Components of the vector of displacement are determined by the functions of three spatial coordinates and time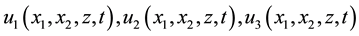 . Components of the tensor of strain are determined by Cauchy correlation. The plate is considered as a three-dimensional body, its material obeying Hooke’s generalized law:
. Components of the tensor of strain are determined by Cauchy correlation. The plate is considered as a three-dimensional body, its material obeying Hooke’s generalized law:
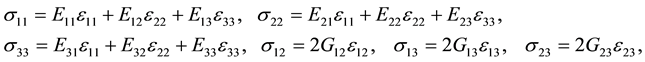 (1)
(1)
where
As an equation of motion of the plate we will use three-dimensional equations of motion of the theory of elasticity:

here
Boundary conditions on the lower and the upper surfaces 



3. Method of Solution
Methods of constructing a bimoment theory of plates is based on displacements expansions in infinite series, Hooke’s generalized law (1), three-dimensional equations of the theory of elasticity (2) and boundary conditions on face surfaces (3). Components of the vector of displacements are expanded in Macloren’s series in the form [3] - [7] :


here

Offered bimoment theory of plates [5] - [8] is described by two unrelated problems, each of which is formulated on the basis of nine two-dimensional equations with corresponding boundary conditions. It should be noted that proposed bimoment theory of plates presents a two-dimensional theory of elastic orthotropic layer, which is deformed in general three-dimensional form.
The first problem is described by two equations relative to longitudinal and tangential forces, by four additionally constructed equations in relation to bimoments and three equations obtained from the boundary conditions (3) on the basis of expansion (4). The forces, moments and bimoments of the plate are determined by nine unknown kinematic functions from relationships [5] - [8] :


We will get the equations of equilibrium relative to longitudinal and tangential forces by integrating two first equations of the theory of elasticity in coordinate z (2):

where




On the basis of force expression (7) two Equations (6) include three unknown functions




Introduce intensities of transversal bimoments 




Introduce intensities of normal bimoments 




Equations in relation to longitudinal and transversal bimoments, acting in plate plane are obtained in the form:


By using series (4) and Formulas (5) are obtained expressions for series’ (4) coefficients 



Equations (6), (11), (12) and (13) make a combined system of differential equations of motion, which consists of nine equations relative to nine unknown functions:
The second problem is described by two equations of moments, one equation of crosscutting forces, three equations of bimoments and three equations, obtained from boundary conditions (3) on the bases of expansion (4). Here forces, moments and bimoments are determined relative to nine unknown kinematic functions in the form [5] - [8] :


The first three of these equations are the ones relative to bending, torsion moments and an equation relative to crosscutting forces, the rest three equations are derived in relation to bimoments.
Multiplying the first and the second equations of the theory of elasticity by coordinate z and integrating it by z, we will obtain an equation of equilibrium in moments and forces:

Integrating the third equation of the theory of elasticity by coordinate z (2), we will obtain an equation of equilibrium in forces:

Bending and torsion moments are determined in the form:



Expressions for crosscutting forces have the form:

In Equations (15) terms with external load are determined by the following formula:
To derive other equations we will introduce the following bimoments, generated at bending and shear of the plate. Bimoments 



Intensity of transversal tangential and normal bimoments 



Equations relative to bimoments at bending and transversal shear are derived in the form:


From expressions for series (4) and Formulas (14) relations for series’ coefficients 



The system of differential equations of motion (15), (20), (21) and (22) makes combined system of nine equations relative to nine unknown functions
Formula to determine the displacements and stresses in the layers of the plate 


Thus, two unrelated problems of bimoment theory of thick plates are formulated in the paper. An accuracy of bimoment theory is defined in dependence on the number of held terms of the series (4). In construction of equations of equilibrium eight terms are held, while for expressions (13) and (22) six terms of each series are held (4). The first equation in (13) and the second equation in (22) are built up to the fourth order relative to small
parameter of the plate
order relative to the parameter.
4. Solution of Tests Problem
As an example consider the problem of static bending of the plate, loaded by normal load:









The values 


here
Solution of the Equations (6), (11), (12) and (13), satisfying boundary conditions (24), is written in the form:

where
Solution of the Equations (15), (20), (21) and (22), satisfying boundary conditions (24), has the form:

Substituting solution (27) into Equations (6), (11), (12) (13), we will obtain the system of linear algebraic equations relative to nine unknown constants
Analysis for orthotropic square plate with elastic characteristics is conducted [1] :
Table 1 and Table 2 give dimensionless numerical results of calculations of displacements and stresses in upper and lower layers of the plate. Maximal values of displacements and stresses of the plate are reached in face surfaces of the pate and are determined by solutions of the first and the second problems.
Table 3 and Table 4 give dimensionless numerical results of displacements and stresses in the middle surface. It should be noted that coefficients of the series with zero indices are displacements
and kinematic functions
Analysis has shown that the values of normal displacement 
Table 1. Values of displacements and stresses in the upper layer of the plate.
Table 2. Values of displacements and stresses in the lower layer of the plate.
Table 3. Values of displacements and rotary angle of a normal in middle surface of the plate.
Table 4. Values of stresses in middle surface of the plate.
5. Conclusion
So on the basis of expansion method, a theory of plates is improved by consideration of bimoments. In the case of spatial deformation of the plate along its thickness, there nonlinear laws of displacements distribution occur, without any simplifying hypotheses. Consequently, existing specified theories of plates and shells, built with a number of simplifying hypotheses could not be used in development of methods of calculation of stresses and displacements of thick plates and shells under the effect of various types of external influences. Calculations of thick plates from anisotropic materials with low strength characteristics could not be made on the basis of classical or specified existing theory. In such cases it is advisable to conduct calculations based on rigorous methodologies developed on the basis of the theory of plates and shells, which takes into account all the components of stress and strain tensor
References
- Ambartsumyan, S.A. (1987) Theory of Anisotropic Plates. Nauka, Moscow, 360 p.
- Galimov, Sh.K. (1976) Specified Theories of Design of Rectangular Theory of Orthotropic Plate under Transversal Load. Studies on the Theory of Plates and Shells, Collection of Papers, Issue ХII, Kazan, 78-84.
- Vlasov, V.Z. (1958) Thin-Walled Spatial System. Gosstroyizdat, Moscow, 503 p.
- Usarov, M.K. (2011) Problem of Bending of Thick Orthotropic Plate in Three-Dimensional Statement. Engineering- Construction Journal, 4, 40-47.
- Usarov, M.K. (2014) Theory of Thick Plates with Consideration of Bimoments. Scientific-Technical Journal of FerPI, 3, 44-50.
- Usarov, M.K. (2014) Analysis of Thick Orthotropic Plates on the Basis of Bimoment Theory. Uzbek Journal of Problems in Mechanics, 2, 41-44.
- Usarov, M.K. (2014) Analysis of Orthotropic Plates on the Basis of Bimoment Theory. Uzbek Journal of Problems in Mechanics, 3-4, 37-41.
- Usarov, M.K. (2014) Bimoment Theory of Bending and Vibrations of Thick Orthotropic Plates. Reports of National University of Uzbekistan, 2/1, 127-132.













