Open Journal of Applied Sciences
Vol.4 No.5(2014), Article ID:44896,9 pages DOI:10.4236/ojapps.2014.45025
New Exact Explicit Solutions of the Generalized Zakharov Equation via the First Integral Method
Yuhuai Sun, Hanlei Hu, Jian Zhang
Institute of Mathematics and Software Science, Sichuan Normal University, Chengdu, China
Email: sunyuhuai63@163.com
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


Received 1 March 2014; revised 3 April 2014; accepted 10 April 2014
ABSTRACT
The generalized Zakharov equation is a coupled equation which is a classic nonlinear mathematic model in plasma. A series of new exact explicit solutions of the system are obtained, by means of the first integral method, in the form of trigonometric and exponential functions. The results show the first integral method is an efficient way to solve the coupled nonlinear equations and get rich explicit analytical solutions.
Keywords:Generalized Zakharov Equation, First Integral Method, Exact Explicit Solutions

1. Introduction
The generalized Zakharov equation have been the focus of many researchers due to two facts: the system is a classic nonlinear mathematic model in plasma physics; the exact solutions to the system are widely applied in many scientific and engineering fields. The generalized Zakharov equation is a coupled equation written as [1]
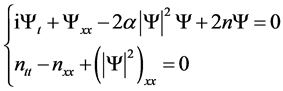 (1)
(1)
where  is the envelope of the high-frequency electric field,
is the envelope of the high-frequency electric field,  is the plasma density measured from its equilibrium value,
is the plasma density measured from its equilibrium value, 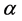 is a real coefficient, x and t are 1-dimensional space and time coordinate, respectively. Up to now, many methods have been used to solve the exact solution of the system (1) such as rational auxiliary equation method [2] , F-expansion method [3] , and Li et al. obtained the generalized solitary solutions by exp-function method [4] [5] , Hong got the doubly periodic solutions by the generalized Jacobi elliptic function expansion method [6] , M. Javidi constructed dark and bright solitary wave solutions by a variational iteration method [7] . Besides, Guo discussed the existence and uniqueness of smooth solution [8] , Gambo investigates the dynamical behavior [9] , S. Abbasbandy solved the numerical solutions [10] of the system (1).
is a real coefficient, x and t are 1-dimensional space and time coordinate, respectively. Up to now, many methods have been used to solve the exact solution of the system (1) such as rational auxiliary equation method [2] , F-expansion method [3] , and Li et al. obtained the generalized solitary solutions by exp-function method [4] [5] , Hong got the doubly periodic solutions by the generalized Jacobi elliptic function expansion method [6] , M. Javidi constructed dark and bright solitary wave solutions by a variational iteration method [7] . Besides, Guo discussed the existence and uniqueness of smooth solution [8] , Gambo investigates the dynamical behavior [9] , S. Abbasbandy solved the numerical solutions [10] of the system (1).
The first integral method is based on the ring theory of commutative algebra, the pioneer work can be traced to Feng, he first proposed the first integral method for solving Burgers-KdV equation [11] and then further developed it. Recently, Bin Lu applied this method to construct travelling wave solutions of the (2 + 1)-dimensional BKK system and (3 + 1)-dimensional Burgers equation [12] , Hodsein et al. also reported new solutions of the Davey-Stewartson equation by using this method [13] , the method has also been successfully adopted for solving some important complex partial differential equations in [14] -[23] .
In order to explore new analysis solutions to the system (1), we attempted to use the first integral method to solve the generalized Zakharov equation for the first time. The rest of the paper proceeds as follows: In Section 2, we briefly introduce the first integral method. In Section 3, we apply the method to the generalized Zakharov equation, and give the exact explicit solutions under two different cases. Finally, some conclusions are given in Section 4.
2. The First Integral Method
Consider the nonlinear partial differential equation (NLPDE) in the form:
 (2)
(2)
where 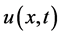 is the solution of Equation (2).
is the solution of Equation (2).
First, we use the travelling wave transformation
 (3)
(3)
where c is a constant to be determined later, then the NLPDE is reduced to a nonlinear ordinary differential system
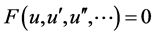 (4)
(4)
where the prime denotes the differential with respect to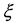 .
.
Next, we introduce new independent variables
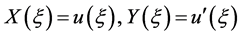 (5)
(5)
then (4) can be converted to a system of the nonlinear ordinary differential system as follows
 (6)
(6)
According to the qualitative theory of ordinary differential equations, the general solutions to (6) can be solved directly if we can find two integrals to (6) under the same conditions. However, it is really difficult to realize this even for one first integral, because for a given autonomous system, there is no systematic theory about how to find its first integral, nor is there a logical way could tell what these first integrals are. A key idea of our approach here is to apply the Division Theorem to obtain one first integral to (6) which reduces (4) to a first-order integrable ODE, then the exact solutions for (2) will be obtained by solving this equation. Now, let’s recall the Division Theorem.
Division Theorem Suppose that 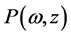 are polynomials in complex domain
are polynomials in complex domain , and
, and 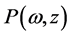 is irreducible in
is irreducible in . If
. If 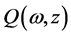 vanishes at all zero points of
vanishes at all zero points of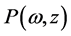 , then there exists a polynomial
, then there exists a polynomial  in
in 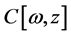 such that
such that 
3. New Exact Explicit Solutions of the Generalized Zakharov Equation
In order to seek the exact solutions of system (1), we assume
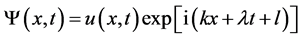 (7)
(7)
Substituting (7) into (1) and yields:
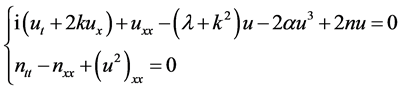 (8)
(8)
Using the transformations
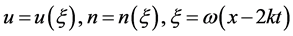 (9)
(9)
where 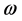 is a nonzero constant, then (8) further reduced to
is a nonzero constant, then (8) further reduced to
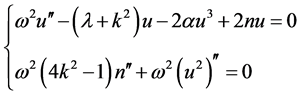 (10)
(10)
where “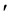 ” denotes
” denotes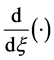 .
.
Integrating Equation (10b) with respect to , and taking the integration constant as zero yields
, and taking the integration constant as zero yields
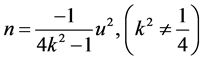 (11)
(11)
Substituting (11) into (10a) and yields:
 (12)
(12)
Now, we introduce new independent variables  which change Equation (12) to a dynamical system given by
which change Equation (12) to a dynamical system given by
 (13)
(13)
Applying the Division Theorem to seek the first integral to (13). Suppose that ,
,  are nontrivial solutions to (13), and
are nontrivial solutions to (13), and 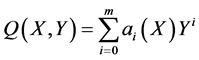 is an irreducible polynomial such that
is an irreducible polynomial such that
 (14)
(14)
where  are polynomials of X and all relatively primes,
are polynomials of X and all relatively primes,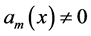 . Equation (14) is called the first integral to (13). Note that
. Equation (14) is called the first integral to (13). Note that 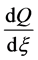 is a polynomial of X and Y, and
is a polynomial of X and Y, and 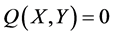 implies
implies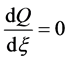 . Due to the Division Theorem, there exists a polynomial
. Due to the Division Theorem, there exists a polynomial  such that
such that
 (15)
(15)
We will take two different cases into consideration in the following, assuming that 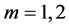 in Equation (15).
in Equation (15).
Case A:
Suppose that , by equating the coefficients of
, by equating the coefficients of  on both sides of (15), we have
on both sides of (15), we have
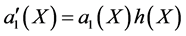 (16a)
(16a)
 (16b)
(16b)
 (16c)
(16c)
Since  are polynomials in
are polynomials in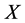 , then from (16a) we deduce that
, then from (16a) we deduce that 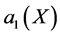 is a constant and
is a constant and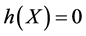 . For simplicity, we take
. For simplicity, we take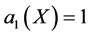 . Balancing the degrees of
. Balancing the degrees of 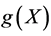 and
and  in (16b), we conclude that
in (16b), we conclude that 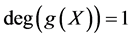 only. Suppose that
only. Suppose that  then from Equation (16b) we find
then from Equation (16b) we find
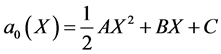 (17)
(17)
where C is an arbitrary integration constant.
Substituting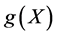 ,
, 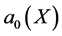 and
and  into Equation (16c) and setting all the coefficients of powers x to be zero, we obtain a system of nonlinear algebraic equations
into Equation (16c) and setting all the coefficients of powers x to be zero, we obtain a system of nonlinear algebraic equations
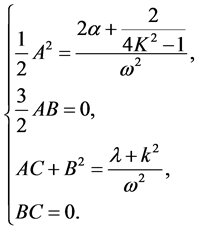 (18)
(18)
By solving it, we obtain
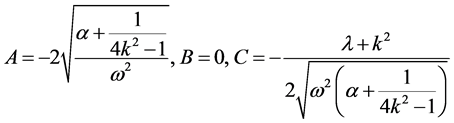 (19a)
(19a)
 (19b)
(19b)
Using the conditions (19a), (19b) in (14) respectively, we obtain
 (20a)
(20a)
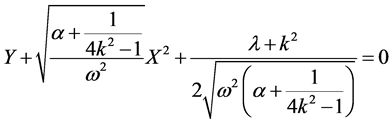 (20b)
(20b)
Combining (20a) with (13), we obtain the exact solutions to (13) as follows
 (21)
(21)
where 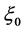 is an arbitrary constant.
is an arbitrary constant.
Then the exact solutions to the system (1) can be written as
 (22)
(22)
Similarly, in the case of (20b), we obtain
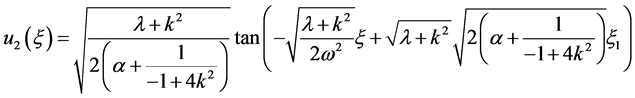 (23)
(23)
where  is an arbitrary constant.
is an arbitrary constant.
Then the exact solutions to the system (1) are given by
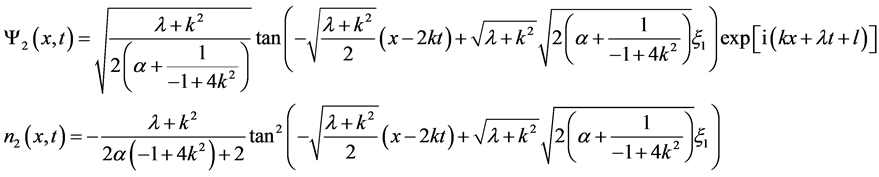 (24)
(24)
We can get distinctive solutions by giving different values to .
.
Case B:
Suppose that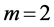 , by equating the coefficients of
, by equating the coefficients of  on both sides of (15), we have
on both sides of (15), we have
 (25a)
(25a)
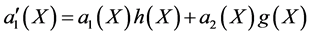 (25b)
(25b)
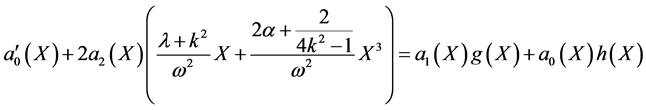 (25c)
(25c)
 (25d)
(25d)
Since 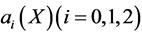 are polynomials, then from (25a) we deduce that
are polynomials, then from (25a) we deduce that  is a constant and
is a constant and . For simplicity, we take
. For simplicity, we take . Balancing the degrees of
. Balancing the degrees of ,
, 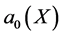 and
and , we conclude that
, we conclude that 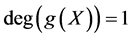 or
or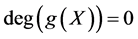 . Actually, if
. Actually, if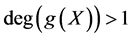 , suppose that
, suppose that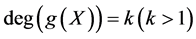 , then from (25b)-(25c), we know
, then from (25b)-(25c), we know ,
, 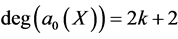 , and from (25d), we have
, and from (25d), we have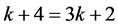 , and then
, and then 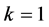 which is contrary to
which is contrary to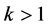 .
.
Case 1 When , we take
, we take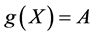 , then from (25b)-(25c), we find
, then from (25b)-(25c), we find

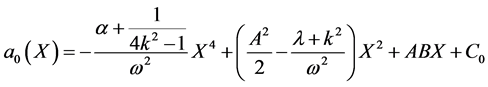
where B, C0 is arbitrary integration constant.
Substituting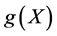 ,
,  and
and 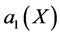 into (25d) and setting all the coefficients of powers of X to be zero, we obtain a system of nonlinear algebraic equations
into (25d) and setting all the coefficients of powers of X to be zero, we obtain a system of nonlinear algebraic equations
 (26)
(26)
By solving it, we obtain
 (27)
(27)
where  is an arbitrary constant.
is an arbitrary constant.
Using the conditions (27) in (14), we obtain
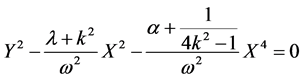 (28)
(28)
Combining (28) with (13), we obtain the exact solutions to (13) as follows
 (29a)
(29a)
 (29b)
(29b)
Then the exact solutions to the generalized Zakharov equation can be written as
 (30)
(30)
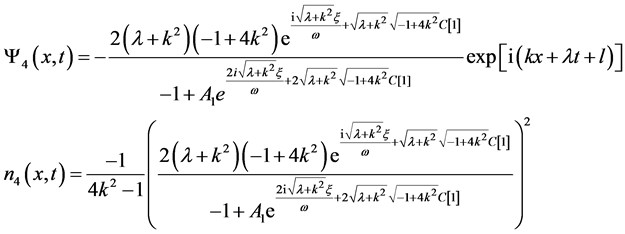 (31)
(31)
Comparing the results with the works studied before, it can be seen these are new results for the system (1).
Case 2 When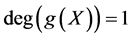 , take
, take , then from (25b)-(25c), we find
, then from (25b)-(25c), we find
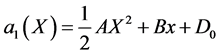
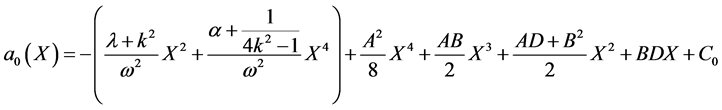
Substituting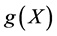 ,
, 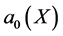 and
and  into (25d), and setting all the coefficients of powers of X to be zero, we obtain a system of nonlinear algebraic equation
into (25d), and setting all the coefficients of powers of X to be zero, we obtain a system of nonlinear algebraic equation
 (32)
(32)
By solving it, we obtain
 (33a)
(33a)
 (33b)
(33b)
Using the conditions (33a), (33b) in (14) respectively, we obtain
 (34)
(34)
i.e.
 (35)
(35)
Combining (35) with (13), we obtain the exact solutions to (13) which were same with the case m = 1.
4. Conclusion
In this paper, we discussed how to construct the exact solutions for the generalized Zakharov equation by using the first integral method. Many new exact explicit solutions with arbitrary constant, peaked wave solutions are obtained, they may be important for the explanation of some practical physical problems. The performance of the method shows it is reliable and effective to give more exact solutions, we deduce that the method can be extended to solve many systems of nonlinear PDE which are arising in the theory of soliton and other fields.
Acknowledgements
This study was technically supported by the National Natural Science Foundation of China under Grant No. 11371267 and the Scientific Research Foundation of the Education Department of Sichuan Province of China under Grant No. 12ZA135.
References
- Malomed, B., Anderson, D., Lisak, M., Quiroga-Teixeiro, M.L. and Stenflo, L. (1997) Dynamics of Solitary Waves in the Zakharov Model Equations. Physical Review E, 55, 962-968. http://dx.doi.org/10.1103/PhysRevE.55.962
- Layeni, O.P. (2009) A New Rational Auxiliary Equation Method and Exact Solutions of a Generalized Zakharov System. Applied Mathematics and Computation, 215, 2901-2907. http://dx.doi.org/10.1016/j.amc.2009.09.034
- El-Wakil, S.A., Degheidy, A.R., Abulwafa, E.M., Madkour, M.A., Attia, M.T. and Abdou, M.A. (2009) Exact Travelling Wave Solutions of Generalized Zakharov Equations with Arbitrary Power Nonlinearities. International Journal of Nonlinear Science, 7, 455-461.
- Li, Y.-Z., Li, K.-M. and Lin, C. (2008) Exp-Function Method for Solving the Generalized-Zakharov Equations. Applied Mathematics and Computation, 205, 197-201. http://dx.doi.org/10.1016/j.amc.2008.05.138
- Borhanifar, A., Kabir, M.M. and Maryam Vahdat, L. (2009) New Periodic and Soliton Wave Solutions for the Generalized Zakharov System and (2 + 1)-Dimensional Nizhnik-Novikov-Veselov System. Chaos, Solitons and Fractals, 42, 1646-1654. http://dx.doi.org/10.1016/j.chaos.2009.03.064
- Hong, B.j., Zhu, W.G. and Lu, D.C. (2012) New Explicit Exact Solutions to the Generalized Zakharov Equations. Journal of Anhui University (Natural Science Edition), 36, 37-42.
- Javidi, M. and Golbabai, A. (2007) Construction of a Solitary Wave Solution for the Generalized Zakharov Equation by a Variational Iteration Method. Computers and Mathematics with Applications, 54, 1003-1009. http://dx.doi.org/10.1016/j.camwa.2006.12.044
- Guo, B.L., Zhang, J.J. and Pu, X.K. (2010) On the Existence and Uniqueness of Smooth Solution for a Generalized Zakharov Equation. Journal of Mathematical Analysis and Applications, 365, 238-253. http://dx.doi.org/10.1016/j.jmaa.2009.10.045
- Betchewe, G., Thomas, B.B., Victor, K.K. and Crepin, K.T. (2010) Dynamical Survey of a Generalized-Zakharov Equation and Its Exact Travelling Wave Solutions. Applied Mathematics and Computation, 217, 203-211. http://dx.doi.org/10.1016/j.amc.2010.05.044
- Abbasbandy, S., Babolian, E. and Ashtiani, M. (2009) Numerical Solution of the Generalized Zakharov Equation by Homotopy Analysis Method. Communications in Nonlinear Science and Numerical Simulation, 14, 4114-4121. http://dx.doi.org/10.1016/j.amc.2010.05.044
- Feng, Z.S. (2002) The First Integral Method to Study the Burgers-Korteweg-de Vries Equation. Journal of Physics A: Mathematical and General Physics, 35, 343-349.
- Lu, B., Zhang, H.Q. and Xie, F.D. (2010) Travelling Wave Solutions of Nonlinear Partial Equations by Using the First Integral Method. Applied Mathematics and Computation, 216, 1329-1336. http://dx.doi.org/10.1016/j.amc.2010.02.028
- Jafari, H., Sooraki, A., Talebi, Y. and Biswas, A. (2012) The First Integral Method and Traveling Wave Solutions to Davey-Stewartson Equation. Nonlinear Analysis: Modelling and Control, 17, 182-193.
- Ke, Y.-Q. and Yu, J. (2005) The First Integral Method to Study a Class of Reaction-Diffusion Equations. Communications in Theoretical Physics, 43, 597-600.
- Hosseini, K., Ansari, R. and Gholamin, P. (2012) Exact Solutions of Some Nonlinear Systems of Partial Differential Equations by Using the First Integral Method. Journal of Mathematical Analysis and Applications, 387, 807-814. http://dx.doi.org/10.1016/j.jmaa.2011.09.044
- Kheiri, H., Hajizadeh, R. and Abbasnezhad, N. (2010) The First Integral Method for Solving Some Nonlinear Equations. Armenian Journal of Physics, 3, 82-97.
- Taghizadeh, N. and Mirzazadeh, M. (2011) The First Integral Method to Some Complex Nonlinear Partial Differential Equations. Journal of Computational and Applied Mathematics, 235, 4871-4877. http://dx.doi.org/10.1016/j.cam.2011.02.021
- El-Sabbagh, M.F. and El-Ganaini, S.I. (2012) The First Integral Method and Its Applications to Nonlinear Equations. Applied Mathematical Sciences, 6, 3893-3906.
- Lu, B. (2012) The First Integral Method for Some Time Fractional Differential Equations. Journal of Mathematical Analysis and Applications, 395, 684-693. http://dx.doi.org/10.1016/j.jmaa.2012.05.066
- Taghizadeh, N., Mirzazadeh, M. and Tascan, F. (2012) The First-Integral Method Applied to the Eckhaus Equation. Applied Mathematics Letters, 25, 798-802. http://dx.doi.org/10.1016/j.aml.2011.10.021
- Rostamy, D., Zabihi, F., Karimi, K. and Khalehoghli, S. (2011) The First Integral Method for Solving Maccari’s System. Applied Mathematics, 2, 258-263. http://dx.doi.org/10.4236/am.2011.22030
- Deng, X.J. (2008) Exact Peaked Wave Solution of CH-γ Equation by the First-Integral Method. Applied Mathematics and Computation, 206, 806-809. http://dx.doi.org/10.1016/j.amc.2008.09.039
- Tascan, F., Bekir, A. and Koparan, M. (2009) Travelling Wave Solutions of Nonlinear Evolution Equations by Using the First Integral Method. Communications in Nonlinear Science and Numerical Simulation, 14, 1810-1815. http://dx.doi.org/10.1016/j.cnsns.2008.07.009

