Open Journal of Applied Sciences
Vol. 3 No. 4 (2013) , Article ID: 35005 , 6 pages DOI:10.4236/ojapps.2013.34040
A Laminar Flow Model for Mucous Gel Transport in a Cough Machine Simulating Trachea: Effect of Surfactant as a Sol Phase Layer
Department of Mathematics, BITS Pilani Hyderabad Campus, Hyderabad, India
Email: dipak@hyderabad.bits-pilani.ac.in, aramu@hyderabad.bits-pilani.ac.in
Copyright © 2013 Dipak Kumar Satpathi, Addepalli Ramu. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received June 3, 2013; revised July 3, 2013; accepted July 10, 2013
Keywords: Mucous gel; Sol Phase; Surfactant; Laminar flow; Trachea; Voigt element
ABSTRACT
In this paper, a planar three layer quasi-steady laminar flow model is proposed in a cough machine which simulates mucous gel transport in model trachea due to mild forced expiration. The flow is governed by the time dependent pressure gradient generated in trachea due to mild forced expiration. Mucous gel is represented by a viscoelastic Voigt element whereas sol phase fluid and air are considered as Newtonian fluids. For fixed airflow rate, it is shown that when the viscosity of mucous gel is small, mucous gel transport decreases as the elastic modulus increases. However, elastic modulus has negligible effect on large gel viscosity. It is also shown that for fixed airflow rate and fixed airway dimension, mucous gel transport increases with the thickness of sol phase fluid and this increase is further enhanced as the viscosity of sol phase fluid decreases. The effect of surfactant is studied by considering sol phase as surfactant layer which causes slip at the wall and interface of sol phase and mucous gel. It is found that in the presence of surfactant mucous gel transport is enhanced.
1. Introduction
Mucociliary clearance is an important pulmonary defense mechanism that serves to remove inhaled substances from the lung. It depends upon the relationship between cilia, mucus and periciliary fluid. The mucociliary function is depressed by a variety of water soluble atmospheric pollutants such as SO2 and NO2 [1]. The presence of surfactant in the mucoserous lining of airways helps in increasing the mucus transport and has been investigated experimentally [2-5]. It was pointed out that surfactant caused relative increase in transport rate [2]. It was also showed that in presence of surfactant mucus transport is more [3,5]. Bronchial surfactant is essential for bronchoalveolar transport mechanisms including ciliary and non-ciliary mucus transport [4]. In [5], Rubin et al. showed that surfactant therapy appears to improve mucus clearability.
In the case of pulmonary diseases (cystic fibrosis, chronic bronchitis, etc.) excessive amount of mucus is formed in the respiratory tract, which is transported mainly by coughing or forced expiration. This transport also depends upon the depths of mucus and serous layers and the rheological properties of mucus [6]. Mucus transport in a cough machine has been studied by a group of investigators under external applied pressure gradient [6-13]. In [7,8], Scherer and Burtz conducted fluid mechanical experiments relevant to coughing, using air and liquid blown out of a straight tube by turbulent jet. They showed that the liquid transport decreases as the viscosity of liquid increases by assuming that the flow is quasi-steady and turbulent stress of air is equal to viscous stress in the liquid. In [9-11], King and co-investigators in their experiments have shown that the transport increases with the increase in the thickness of mucous gel air flow rate and with the decrease in its elastic modulus. It was observed that mucous gel transport in a simulated cough machine increases as the viscosity of serous layer simulates decreases [6,12,13].
It may be noted that no mathematical model is developed so far to explain the above experimental observations, particularly with surfactant as a sol phase layer. In view of this, in this paper, we present a quasi-steady state three layer laminar flow model (mucous gel as viscoelastic Voigt element, air and surfactant sol phase fluid as Newtonian fluids) for mucous gel transport in a cough machine simulating trachea by considering the surfactant sol phase as serous layer. Due to the presence of surfactant, the slip effects at the boundaries of the surfactant layer are taken into account in the model. It is assumed that the gel transport is caused by a time dependent pressure gradient due to mild forced expiration.
2. Modelling and Solution
We consider the quasi-steady state simultaneous laminar flow of surfactant sol phase fluid, viscoelastic mucous gel and air in a rectangular channel, relevant to mucous gel transport in a cough machine simulating a model trachea. The flow assumed to be caused by a time dependent pressure gradient generated by air motion simulating mild forced expiration in trachea. The flow geometry is shown in Figure 1, where surfactant sol phase fluid 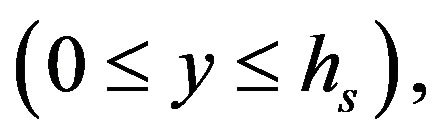 mucous gel
mucous gel 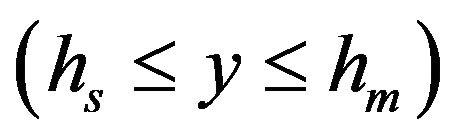 and air
and air 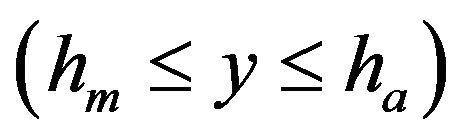 regions are indicated.
regions are indicated.
The equations governing the laminar flow of surfactant sol phase fluid, viscoelastic mucous gel and air under quasi-steady state condition can be written as follows:
Region I 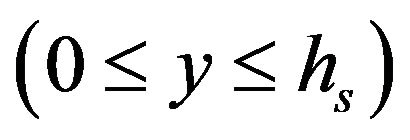 surfactant sol phase
surfactant sol phase
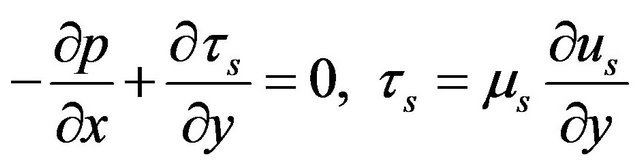 (1)
(1)
Region II 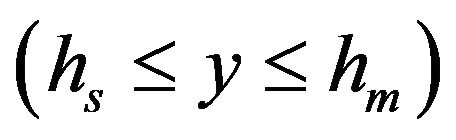 mucous gel
mucous gel
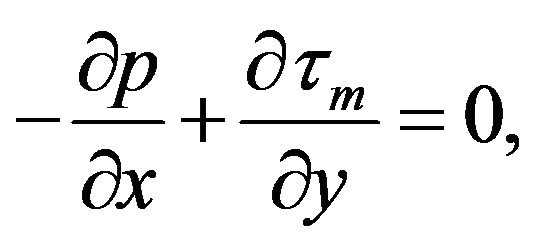 (2)
(2)
 (3)
(3)
Region III 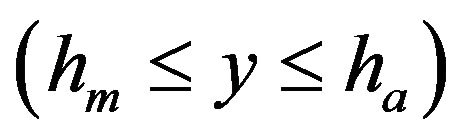 air
air
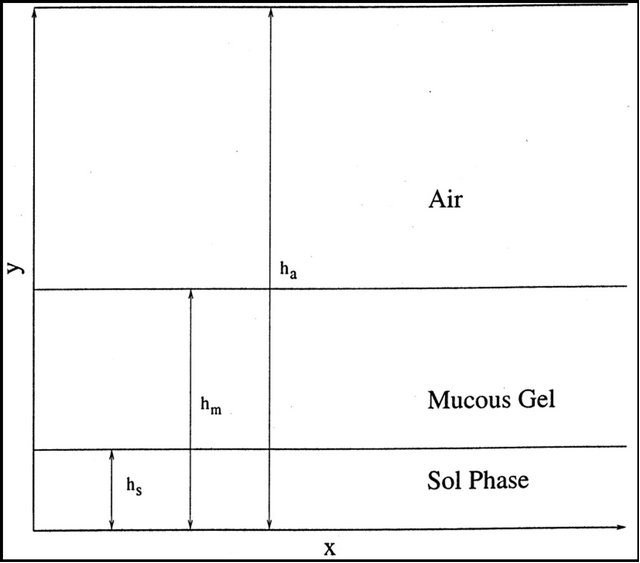
Figure 1. Flow geometry.
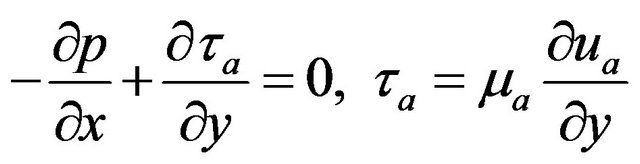 (4)
(4)
where  is the time,
is the time, ![]() is the coordinate in the direction of the flow,
is the coordinate in the direction of the flow, ![]() is the co-ordinate perpendicular to fluid flow,
is the co-ordinate perpendicular to fluid flow, ![]() is the pressure;
is the pressure;  are the velocity components of sol phase fluid, mucous gel and air in the flow direction;
are the velocity components of sol phase fluid, mucous gel and air in the flow direction; 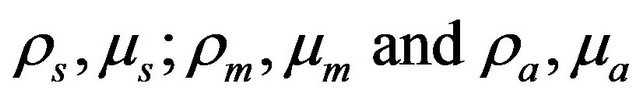 are their respective densities and viscosities, G is the elastic modulus of mucous gel and
are their respective densities and viscosities, G is the elastic modulus of mucous gel and 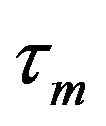 is the shear stress in the mucous gel layer;
is the shear stress in the mucous gel layer; 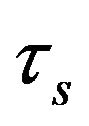 is the shear stress in the sol phase layer and
is the shear stress in the sol phase layer and 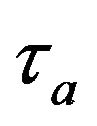 is the shear stress in the air region. It is assumed that mucous gel behaves like a viscoelastic Voigt element whose constitutive equation is given by equation (3) [14].
is the shear stress in the air region. It is assumed that mucous gel behaves like a viscoelastic Voigt element whose constitutive equation is given by equation (3) [14].
Mild forced expiration is a short time phenomena and a time dependent pressure gradient is generated in trachea. Therefore, we assume that
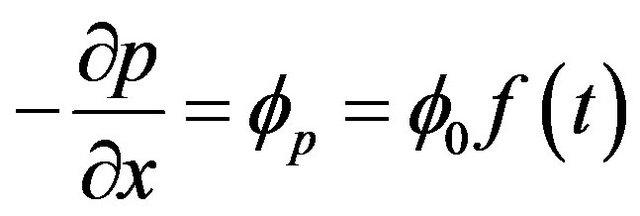 (5)
(5)
and 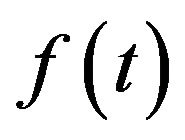 is given by
is given by
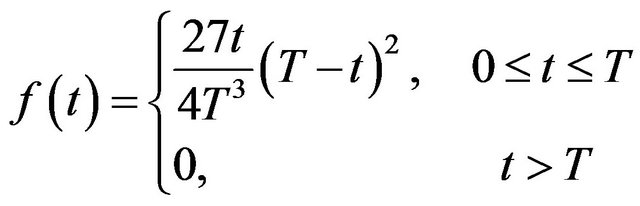
where  is the time, T is the duration of mild forced expiration and
is the time, T is the duration of mild forced expiration and 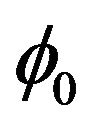 is a constant (independent of time). The function
is a constant (independent of time). The function 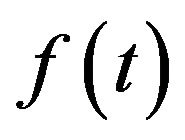 is plotted in Figure 2 for various T.
is plotted in Figure 2 for various T.
Since initially there is no pressure gradient, one can assume that the velocities and stresses are zero, therefore, the initial conditions are
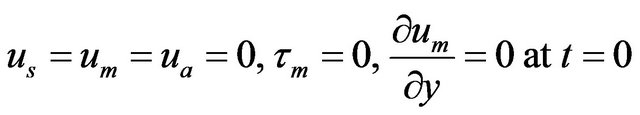 (6)
(6)
The boundary and matching conditions for the system (1) - (4) can be written as follows:
Boundary conditions:
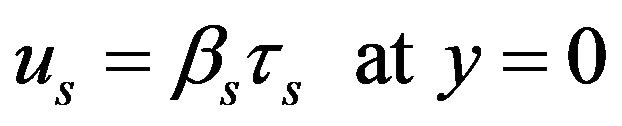 (7)
(7)
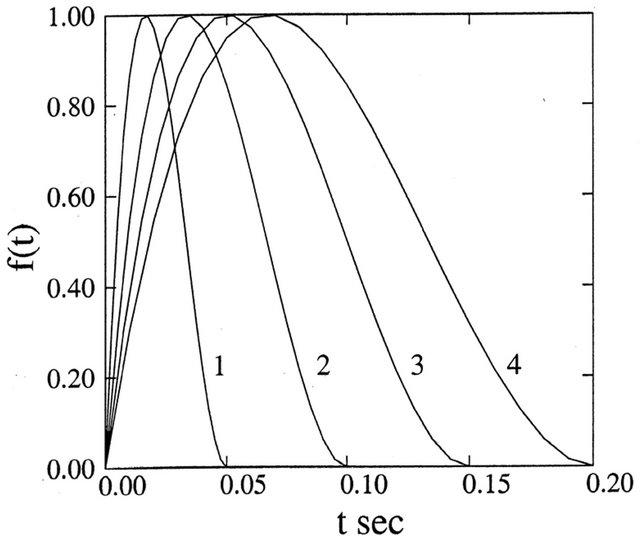
Figure 2. Graph of 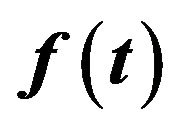 for various
for various![]() .
.
 (8)
(8)
Matching conditions:
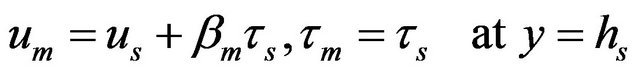 (9)
(9)
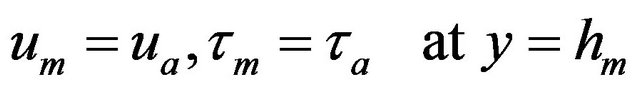 (10)
(10)
In equation (7) the right hand side represents the slip velocity at the surface 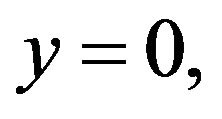 which is caused by the slipperiness of the surfactant sol phase. Similarly in equation (9), the second term on the right hand side represents slip velocity at the interface
which is caused by the slipperiness of the surfactant sol phase. Similarly in equation (9), the second term on the right hand side represents slip velocity at the interface 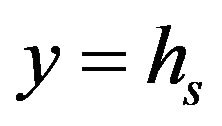 and thus the condition of the continuity of the velocities at the interface
and thus the condition of the continuity of the velocities at the interface  is still valid.
is still valid. 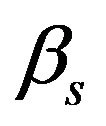 and
and 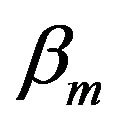 in equations (7) and (9) are called the slip coefficients [15]. The corresponding slip velocities increase as slip coefficients increase. In a particular case, when
in equations (7) and (9) are called the slip coefficients [15]. The corresponding slip velocities increase as slip coefficients increase. In a particular case, when 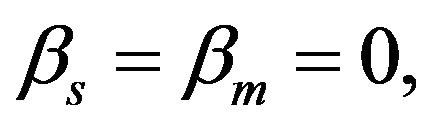 the conditions (7) and (9) reduce to usual no-slip conditions.
the conditions (7) and (9) reduce to usual no-slip conditions.
Calculation of Flow Rates
Solving the equations (1)-(4) along with the initial, boundary and matching conditions (6)-(10), the expressions for the velocity components can be found as the following.
 (11)
(11)
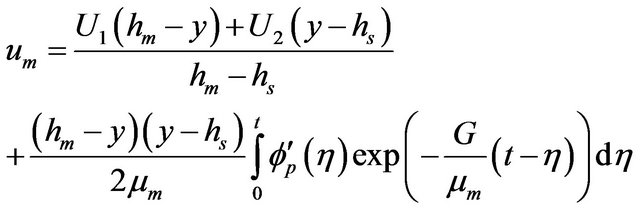 (12)
(12)
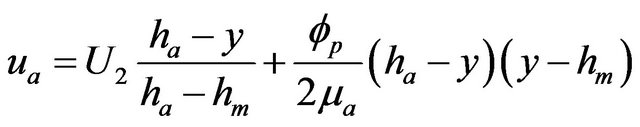 (13)
(13)
here,  denotes the differentiation of
denotes the differentiation of 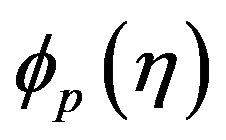 with respect to
with respect to 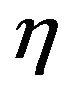 and the expressions for
and the expressions for 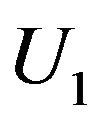 and
and  are given by the following.
are given by the following.
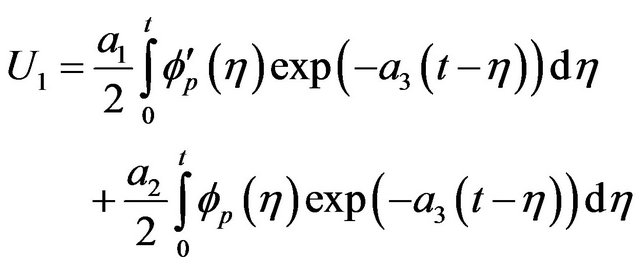 (14)
(14)
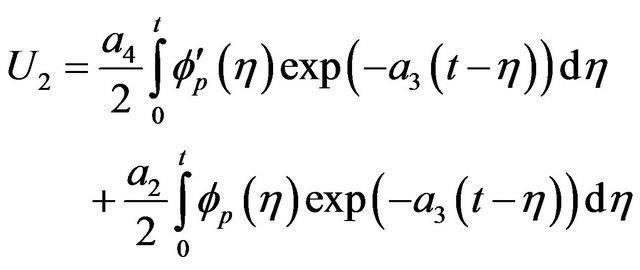 (15)
(15)
where
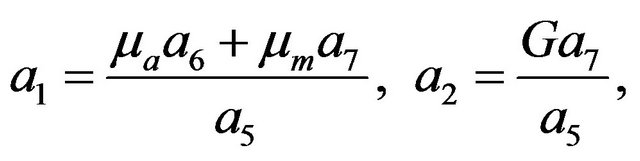

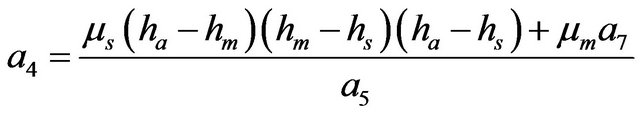
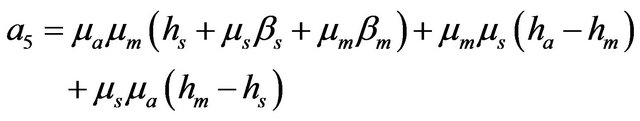

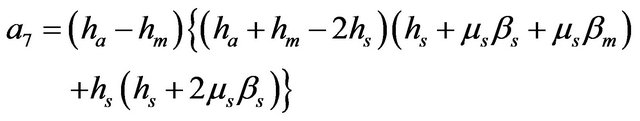
The Volumetric flow rates per unit thickness in each of the layer are
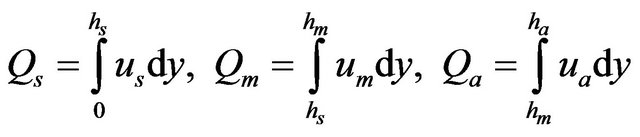
which after using equations (11)-(13) can be found as
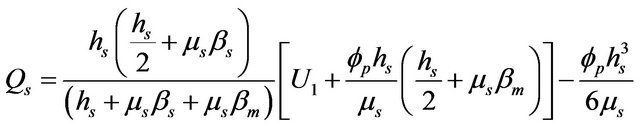
(16)
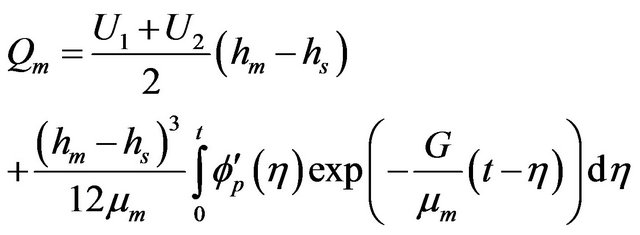 (17)
(17)
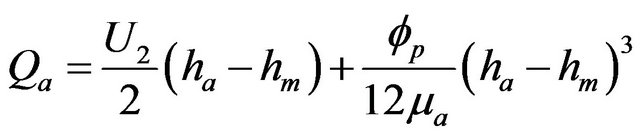 (18)
(18)
The average flow rates in each layer can be defined as

which after using equations (16)-(18) can be written as
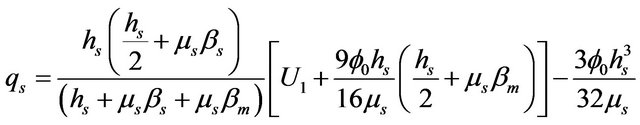 (19)
(19)
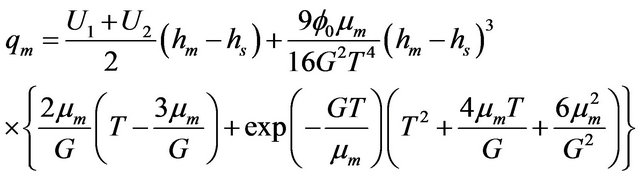 (20)
(20)
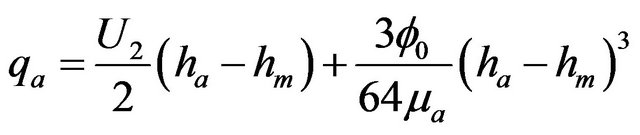 (21)
(21)
Where,
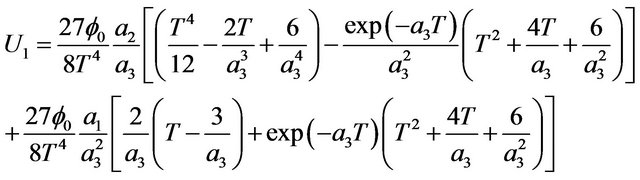
(22)
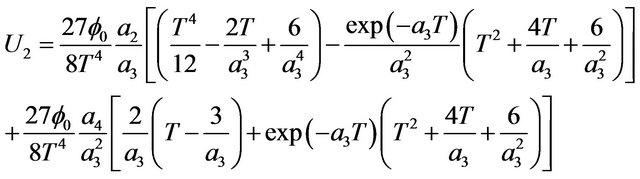
(23)
In a particular case, when mucus behaves as a Newtonian fluid i.e.  the expressions for
the expressions for 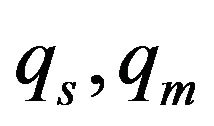 and
and 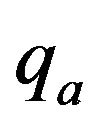 reduce to
reduce to
 (24)
(24)
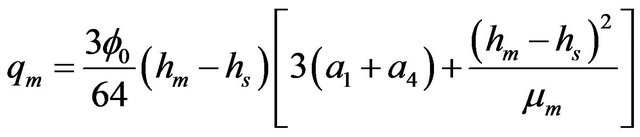 (25)
(25)
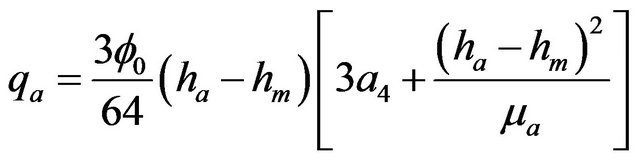 (26)
(26)
3. Results and Discussion
The effects of rheological properties of mucous gel and its thickness, viscosity and thickness of sol phase fluid, slipperiness caused by surfactant sol phase and air flow rate on mucous gel flow rate are shown by plotting the expressions for 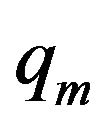 given by equation. (20) in Figures 3-6( after eliminating
given by equation. (20) in Figures 3-6( after eliminating 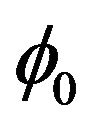 with the help of equation (21)). The values of various parameters are taken as in the following [6,10,16-20].
with the help of equation (21)). The values of various parameters are taken as in the following [6,10,16-20].
Diameter of model trachea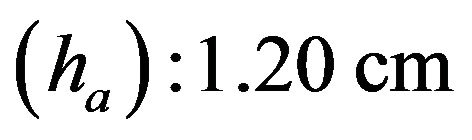 .
.
Thickness of mucous gel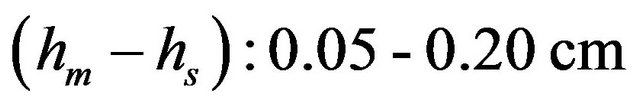 .
.
Thickness of sol phase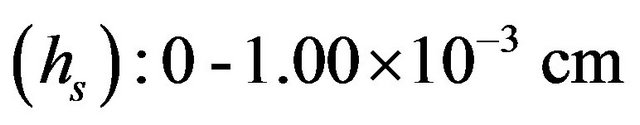 .
.
Viscosity of air .
.
Viscosity of mucous gel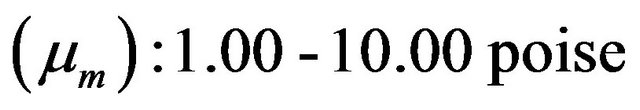 .
.
Viscosity of sol phase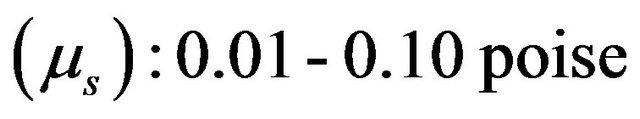 .
.
Elastic modulus of mucous gel (G):
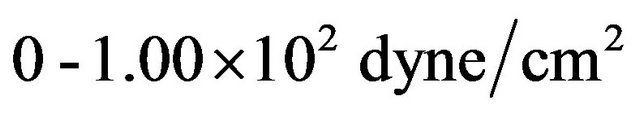 .
.
 (a)
(a)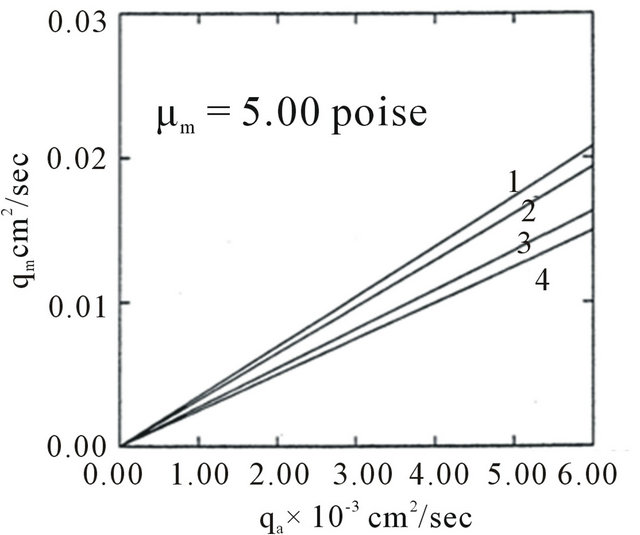 (b)
(b) (c)
(c)
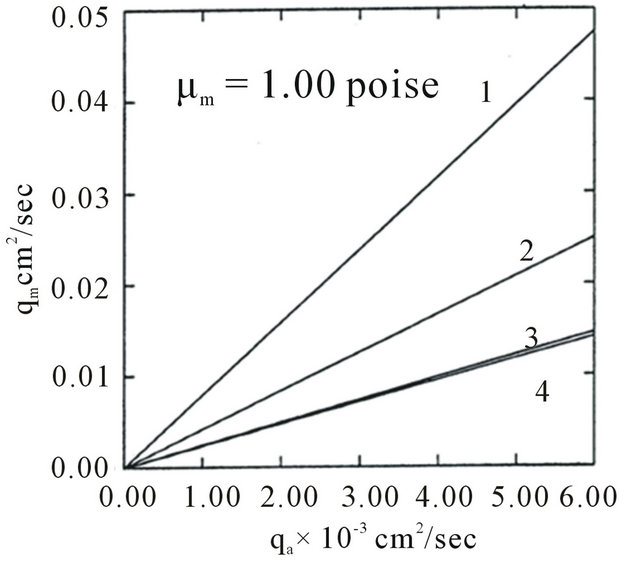
Figure 3. Variation of 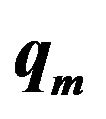 with
with 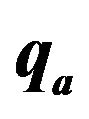 for different
for different 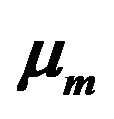 and
and 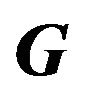 (1, 2, 3, 4 correspond to G = 0.10, 50, 100 units respectively).
(1, 2, 3, 4 correspond to G = 0.10, 50, 100 units respectively).
In our calculation, we assume
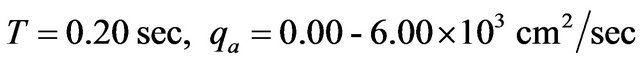 and
and .
.
Figure 3 is a plot of mucous gel flow rate versus airflow rate for different  From this figure, it is observed that the effect of elastic modulus depends upon the magnitude of the viscosity of mucous gel. For less viscous mucous gel, Figure 3(a) shows that the gel flow rate decreases as the elastic modulus increases. This implies that the flow rate decreases when mucous gel becomes more elastic, suggesting that the efficient transfer
From this figure, it is observed that the effect of elastic modulus depends upon the magnitude of the viscosity of mucous gel. For less viscous mucous gel, Figure 3(a) shows that the gel flow rate decreases as the elastic modulus increases. This implies that the flow rate decreases when mucous gel becomes more elastic, suggesting that the efficient transfer
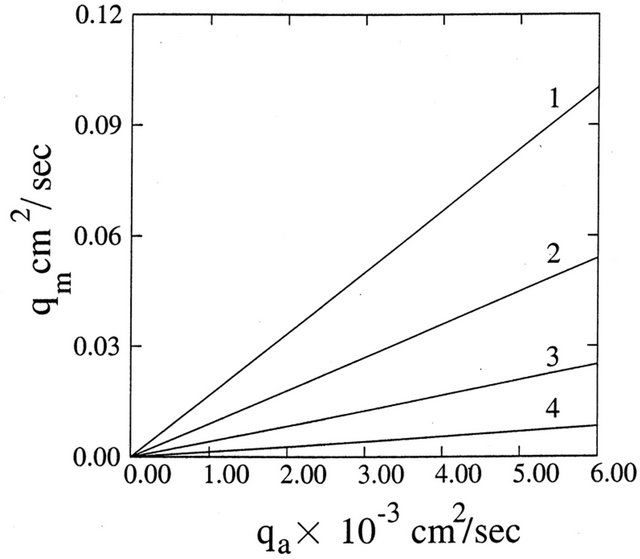
Figure 4. Variation of 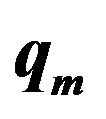 with
with 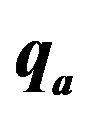 for different
for different  (1, 2, 3, 4 correspond to
(1, 2, 3, 4 correspond to  units respectively).
units respectively).
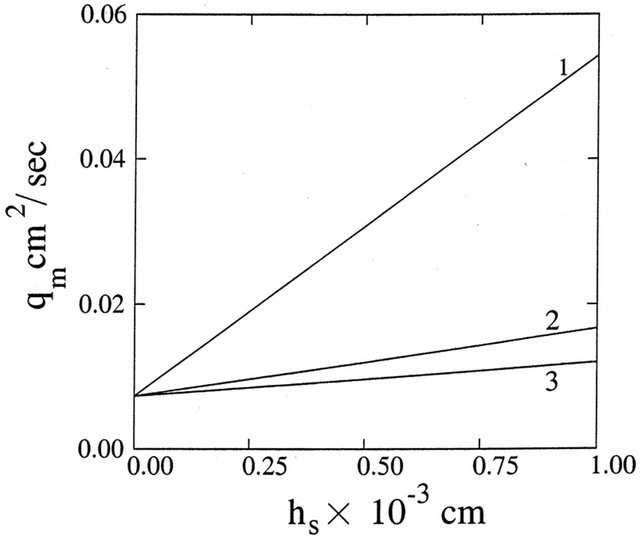
Figure 5. Variation of 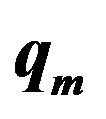 with
with 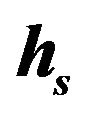 for different
for different 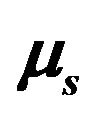 (1, 2, 3, 4 correspond to
(1, 2, 3, 4 correspond to 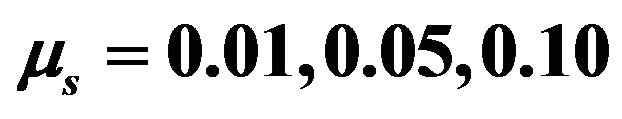 units respectively).
units respectively).

Figure 6. Variation of 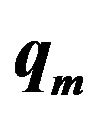 with
with 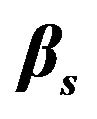 for different
for different 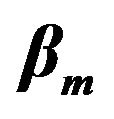 (1, 2, 3 correspond to
(1, 2, 3 correspond to 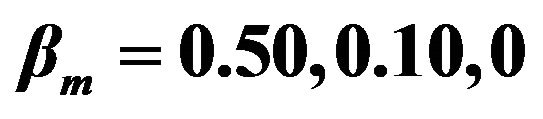 units respectively).
units respectively).
of energy from the air flow to the mucous gel is impeded by the elastic recoil behavior of the mucous gel [9,10]. However for large gel viscosity, from Figure 3(c) it is observed that there is negligible effect of elastic modulus on mucous gel flow rate. Therefore, if mucous gel is represented by a Voigt element, gel transport will be more in the Newtonian case than that of viscoelastic case for less viscous mucous gel [21]. Again comparing Figures (a)-(c), it is noted that mucous gel flow rate decreases as its viscosity increases for small elastic modulus of mucous gel, but viscosity has negligible effect for large elastic modulus of mucous gel. The former result is in conformity with the experimental observations of [7,8,11], who noted that gel flow rate decreases as its viscosity increases. Figure 3 also shows that mucous gel flow rate increases with the flow rate of air [9,10]. It may be remarked here that due to the assumption of laminar flows of air and mucous gel, only a lower limit of mucous gel flow rate is obtained by our model as in the case of simulated cough machine (where turbulent flow of air occurs).
The effects of mucous gel thickness and sol phase fluid on mucous gel flow rate are shown in Figures 4 and 5 for fixed dimensions of model trachea. From Figure 4 it is observed that mucous gel flow rate increases with its thickness. This is in conformity with the experimental observations of [6,9,11,22] and analytical observations of [20,23]. Figure 5 demonstrates the role of sol phase on mucous gel flow rate. This figure shows that the gel flow rate increases as the depth of sol phase increases and this increase is further enhanced as the viscosity of sol phase decreases [6,12,13,21].
The effect of slipperiness caused by surfactant sol phase is shown in Figure 6. This figure shows that gel flow rate increases with the increase of slip coefficients. Therefore, in the presence of surfactant sol phase, the gel flow rate is more. Thus, it is reasonable to speculate that a lubricant introduced between the mucous layer and walls of the airways could increase the mucus flow rate during forced expiration. Thus, the role of surfactant is to spread and cover the entire surface of the relevant airway and thereby serve as an adhesive forming an interface or interlayer between mucus and the airway wall [24,25].
4. Conclusion
From the above discussion, it is concluded that the mucous gel transport increases as the slip velocity at boundary surfaces of surfactant sol phase layer increases. Therefore the role of surfactant in the mucous gel transport can be speculated as a lubricating agent acting as a serous layer and reducing the friction between the mucus layer and the surfaces of the epithelium embedded with cilia. It also observed that the gel flow rate increases with the air flow rate. For fixed airflow rate, the effect of elastic modulus on mucous gel transport depends upon the magnitude of mucous gel viscosity. For small viscosity, it increases as the elastic modulus decreases. However, elastic modulus has negligible effect on large viscosity of mucous gel. Mucous gel transport also increases with its thickness for fixed dimension of trachea and air flow rate. For fixed dimension of trachea and mucus thickness, mucous gel flow rate increases as the thickness of surfactant sol phase fluid increases for a given value of the air flow rate. This increase is further enhanced as the viscosity of sol phase fluid decreases and as the thickness of mucous gel layer increases. We hope that this study will throw some light on the role of surfactant in mucus transport in the airways due to forced expiration or cough.
REFERENCES
- Wanner, “Clinical Aspects of Mucociliary Transport,” American Review of Respiratory Disease, Vol. 116, No. 1, 1977, pp. 73-125.
- L. Allegra, R. Bossi and P. Barga, “Influence of Surfactant on Mucociliary Transport,” European Journal of Respiratory Diseases, Vol. 67, Suppl. 142, 1985, pp. 71-76.
- H. Kai, M. Saito, K. Furuswa, Y. Oda, Y. Okano, K. Takahama and T. Miyata, “Protective Effect of Surface Active Phospholipids against the Acid inducing Inhibitions of the Tracheal Mucociliary Transport,” The Japanese Journal of Pharmacology, Vol. 49, No. 3, 1989, pp. 375- 380. doi:10.1254/jjp.49.375
- Lachmann, “Possible Function on Bronchial Surfactant,” European Journal of Respiratory Diseases, Vol. 67, No. 142, 1985, pp. 49-60.
- K. Rubin, O. Ramirez and M. King, “Mucus Rheology and Transport in Neonatal Respiratory Distress Syndrome and the Effect of Surfactant Therapy,” Chest, Vol. 101, No. 4, 1992, pp. 1080-1085. doi:10.1378/chest.101.4.1080
- M. Agarwal, M. King, B. K. Rubin and J. B. Shukla, “Mucus Transport in a Miniaturized Simulated Cough Machine: Effect of Constriction and Serous Layer Simulant,” Biorheology, Vol. 26, No. 6, 1989, pp. 977-988.
- P. W. Scherer and L. Burtz, “Fluid Mechanical Experiments Relevant to Coughing,” Journal of Biomechanics, Vol. 11, No. 4, 1978, pp. 183-187. doi:10.1016/0021-9290(78)90011-8
- P. W. Scherer, “Mucus Transport by Cough,” Chest, Vol. 80, Suppl. 6, 1981, pp. 830-833. doi:10.1378/chest.80.6.830
- M. King, “The role of Mucus Viscoelasticity in Cough Clearance,” Biorheology, Vol. 24, No. 6, 1987, pp. 589- 597.
- M. King, G. Brock and C. Lundell, “Clearance of Mucus by Simulated Cough,” Journal of Applied Physiology, Vol. 58, No. 6, 1985, pp. 1176-1182.
- M. King, J. M. Zahm, D. Pierrot, S. Vaquez-Girod and E. Puchelle, “The Role of Mucus Gel Viscosity, Spinability and Adhesive Properties in Clearance by Simulated Cough,” Biorheology, Vol. 26, No. 4, 1989, pp. 737-745.
- J. M. Zahm, D. Pierrot, C. Duvivier, M. King and E. Puchelle, “Influence of Airway Surface Liquid (Sol Phase) on Clearance by Cough,” Biorheology, Vol. 26, No. 4, 1989, pp. 747-752.
- M. Agarwal, M. King and J. B. Shukla, “Mucous Gel Transport in a Simulated Cough Machine: Effects of Longitudinal Grooves Representing Spacing between Arrays of Cilia,” Biorheology, Vol. 31, No. 1, 1994, pp. 11-19.
- W. L. Wilkinson, “Non-Newtonian Fluids,” Pergamon Press, London, 1960.
- A. H. P. Skelland, “Non-Newtonian Flow and Heat Transfer,” John Wiley and Sons Inc., New York, 1967.
- S. S. Davis and J. E. Dippy, “The Rheological Properties of Sputum,” Biorheology, Vol. 6, No. 1, 1969, pp. 11-21.
- S. M. Ross and S. Corssin, “Results of an Analytical Model of Mucociliary Pumping,” Journal of Applied Physiology, Vol. 37, No. 3, 1974, pp. 333-340.
- A. Silberberg, “Biorheological Matching: Mucociliary Interaction and Epithelial Clearance,” Biorheology, Vol. 20, No. 2, 1983, pp. 215-222.
- B. Yeates, “Mucus Rheology,” In: R. G. Crystal and J. B. West, Eds., The lung: Scientific Foundations, Raven, New York, 1991, pp. 197-203.
- D. K. Satpathi, B. V. Rathish Kumar and P. Chandra, “Unsteady Sate Laminar Flow of Viscoelastic Gel and Air in a Channel: Application to Mucus Transport in a Cough Machine Simulated Trachea,” Mathematical and Computer Modeling, Vol. 38, No. 1-2, 2003, pp. 63-75. doi:10.1016/S0895-7177(03)90006-9
- D. K. Satpathi, “Mathematical Modeling of Mucus Transport in the Lung under Pathological and Normal Conditions,” PhD thesis, Indian Institute of Technology, Kanpur, 1998.
- P. Camner, B. Mossberg, K. Philipson and G. Strandberg, “Elimination of Test Particles from Human Tracheobronchial Tract by Voluntary Coughing,” Scandinavian Journal of Respiratory Diseases, Vol. 60, No. 2, 1979, pp. 56- 62.
- A. Saxena, A. P. Tyagi and R. Saxena, “Mathematical Modeling of Mucus Transport in the Lung Due to Prolonged Cough: Effect of Resistance to Flow by Serous Fluid in Cilia Bed,” International Journal of Mathematical Science, Vol. 10, No. 1-2, 2011, pp. 9-20.
- H. Rensch and H. Von Seefeld, “Surfactant Mucus Interaction in Pulmonary Surfactant,” In: B. Robertson, L. M. G. Von Golde and J. J. Batunberg, Eds., Pulmonary Surfactant: From Molecular Biology to Clinical Practice, Elsevier Science Publishers, Amsterdam, 1984, pp. 203- 214.
- R. Banerjee and R. R. Puniyani, “Analysis of Dynamic Surface Properties of Therapeutic Surfactants and Lung Phospholipids,” Journal of Biomaterials Applications, Vol. 14, No. 3, 2000, pp. 243-272. doi:10.1106/9D4B-L6PP-7CTF-BY8G

