ABSTRACT

This paper is to extend the Poincar’e Lemma for differential forms in a bounded, convex domain [1] in Rⁿ to a more general domain that, we call, is deformable to every point in itself. Then we extend the homotopy operator T in [1] to the domain defromed to every point of itself.

1. Introduction

In [2], we have the Converse of the Poincar’e Lemma:

Lemma 1.1. Let U be a domain in 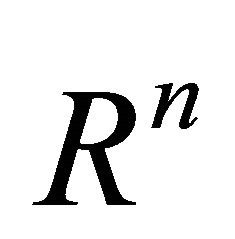which can be deformed to a point P. Let ω be a (p+1)-form on U such that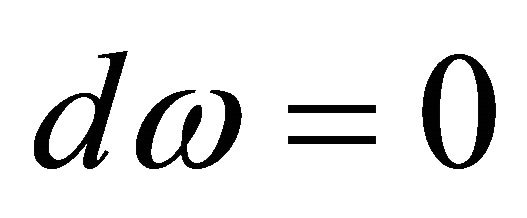. Then there is a p-form in U such that

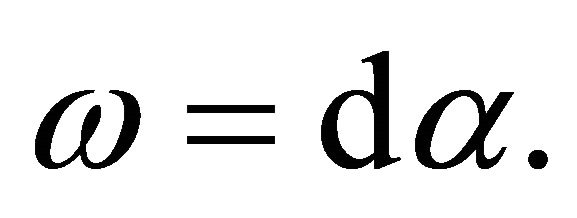(1)

And in [1] we have Lemma 1.2. Let D be a bounded, convex domain in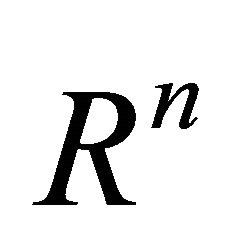. To each 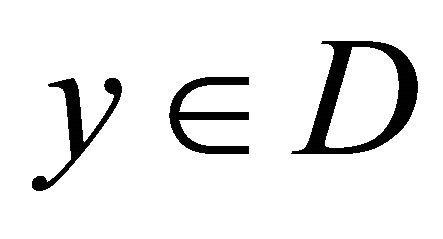there corresponds a linear operator defined by

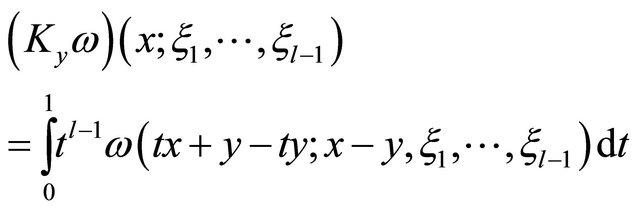(2)

and the decomposition

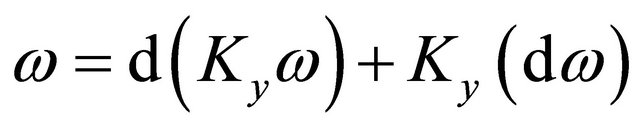(3)

holds at any point y in D.

In this paper, we extend the results of both of them. First we extend the bounded, convex domain D to the domain that deformed to every interior point. Then we not only gain that the closed form is the exact form, but every form can be decomposited to two parts where one of them is an exact form and another is a form related to the exterior differential of the form.

2. Preliminaries

It’s well-known that differential forms are the generalizations of the functions and have been applied to many fields such as potential theory, partial differential equations, quasiconformal mappings, nonlinear analysis, electromagnetism and control theory. First, we introduce some notations and preliminaries about differential forms. Let U denote an open subset of 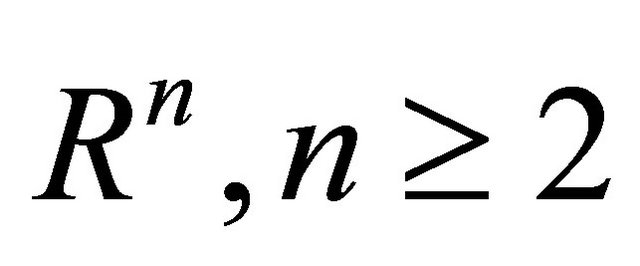and. Let 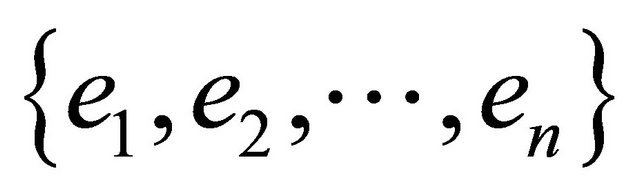denote the standard orthogonal basis of Rⁿ. 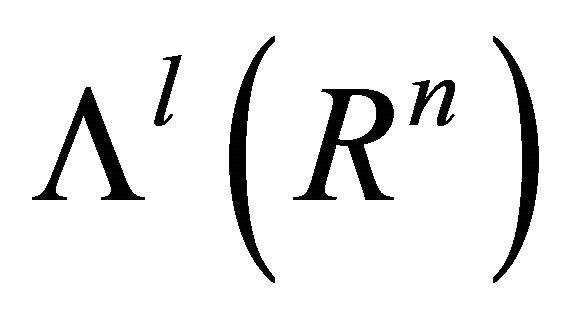is the linear space of l-covectors, generated by the exterior products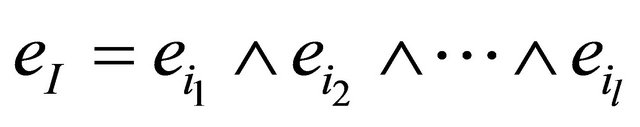, corresponding to all ordered l-tuples . The Grassman algebra 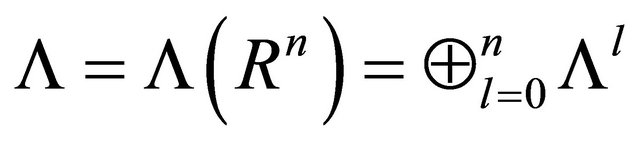is a graded algebra with respect to the exterior products.

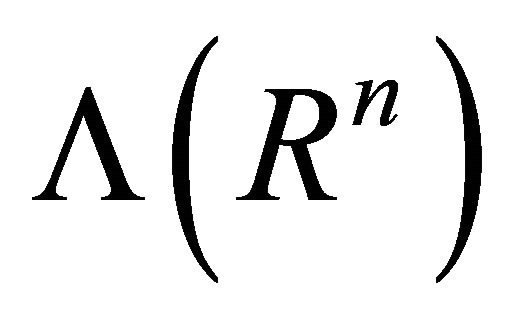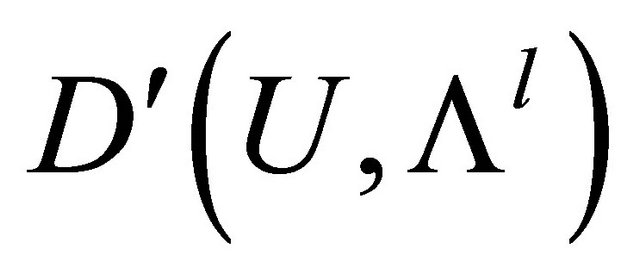A differential l-form ω on U is a Schwartz distribution on U with values in. Let denote the space of all differential l-forms and the class of infinitely differentiable l-forms on U by.

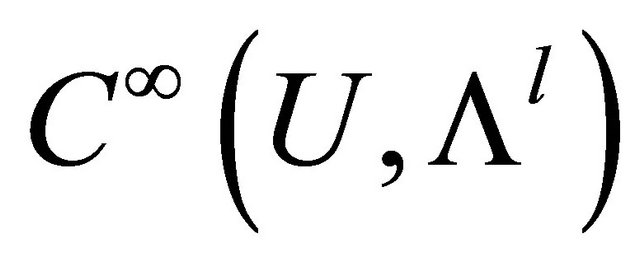Then we define the mapping f^* for a smooth mapping f on U into V, where U is a domain in 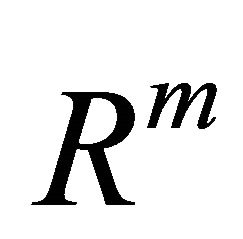and V is a domain in, that is

(4)

We denote by the coordinates of R^m and by the coordinates of Rⁿ. Then we can write

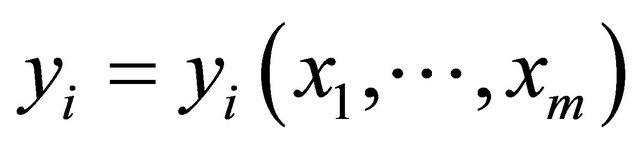(5)

to show that the point with coordinates x is transformed by f to the point with coordinated y. The function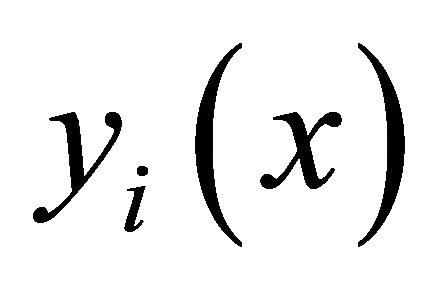 are smooth. Now we define the map f^* taking l-forms on V to l-forms on U:

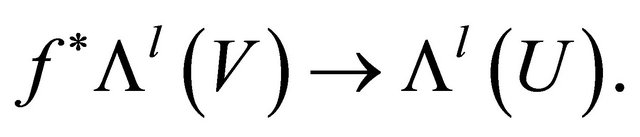(6)

And there are basic properties for the mapping we’ll use in the following statement.

Lemma 2.1. If ω is a l-form on V, then

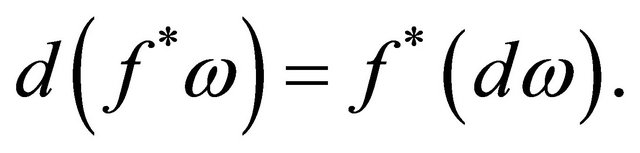(7)

Lemma 2.2. If and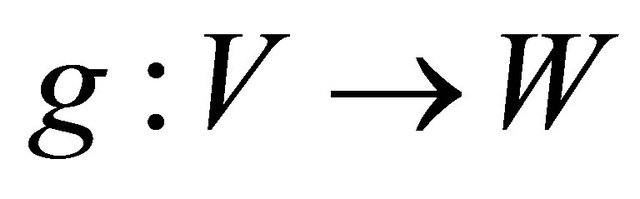, then

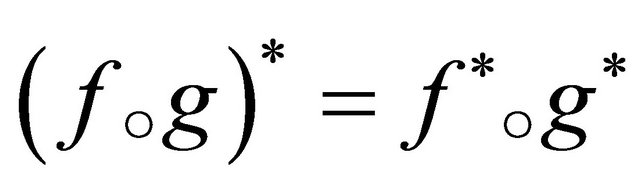(8)

More essential properties for 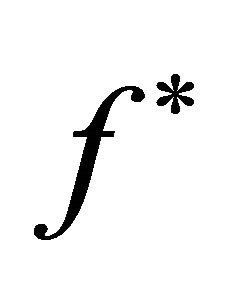can be found in [3]. More preliminaries of differential forms and their applications can be found in [1-15].

Then we define another important mapping:

Definition 2.1. Given a function 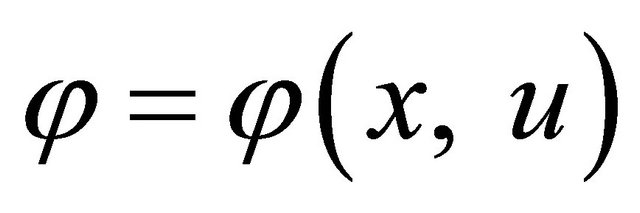is a continuous for (x, u) [3]. We call a domain U is deformable to a point p if there exists such that

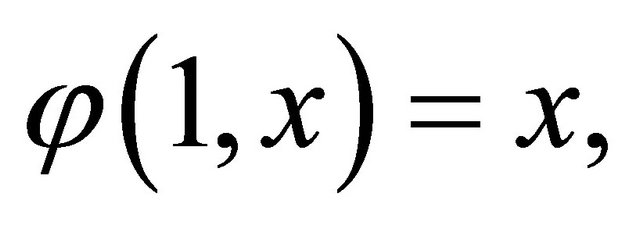(9)

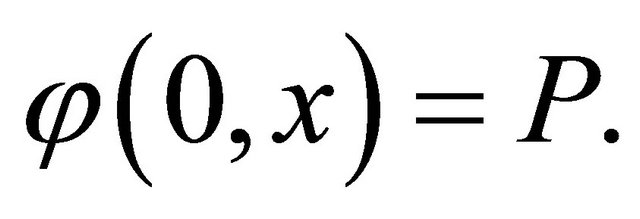(10)

Then we can analogously define that a domain is deformable to any point, and denote the function 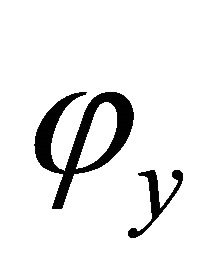as for every y.

3. Main Results and Proofs

First, we introduce the “cylinder construction”. Let U be a domain in 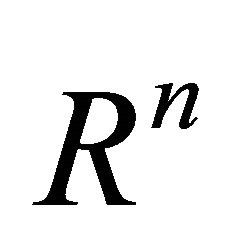that is deformable to any 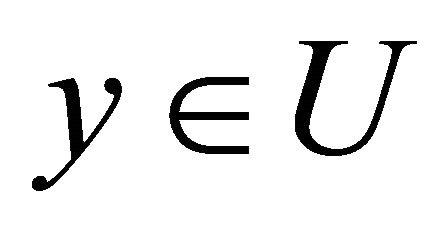just like we have defined. We denote by [0, 1] the unit interval on the t-axis and consider the cylinder or product space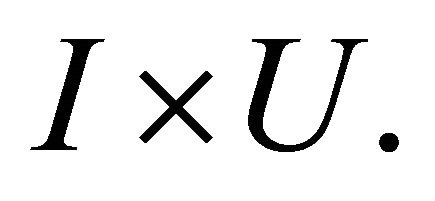

This consists of all pairs (t, x) where and x runs over points of U. We point out the two maps which identify U with the top and bottom of the cylinder, that is

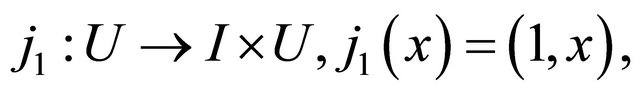(11)

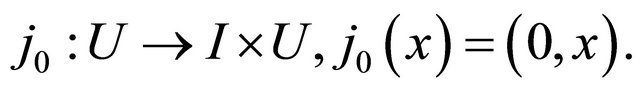
Thus

(12)

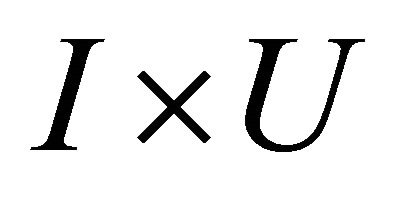For example, to form where ω is a form on, we simply replace t by 1 wherever it occurs in ω (and dt by 0 correspondingly). Now we form a new operation 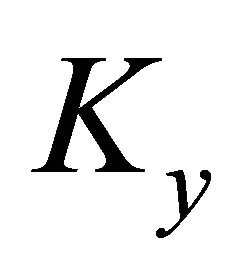for any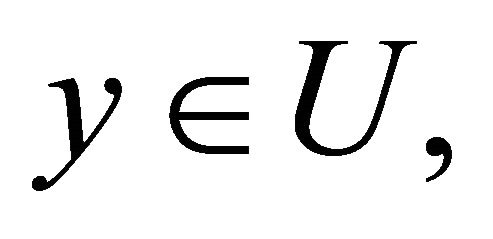

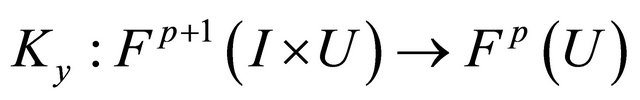(13)

is defined on monomials by the formulas:

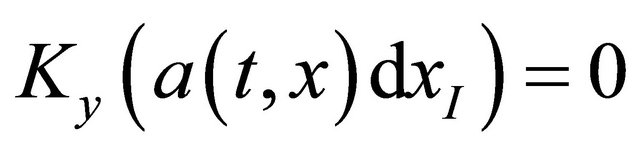(14)

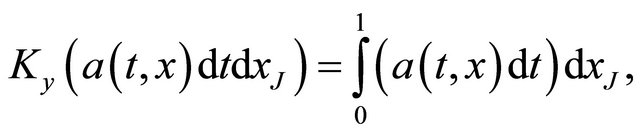(15)

and on general differential forms by summing the results on the monomial parts. Here is the basic property of: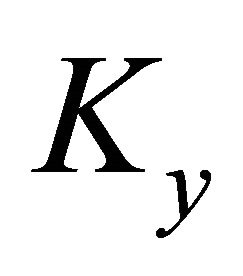

Lemma 3.1. If ω is any (p+1)-form on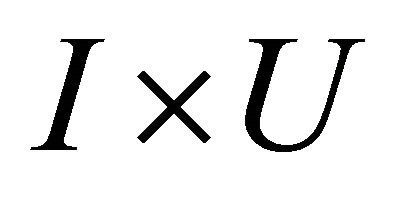, then

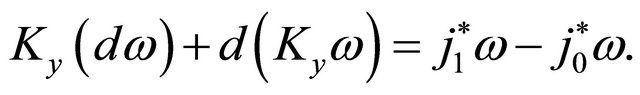(16)

Proof: We only need to check this for monomials.

Case 1.

We have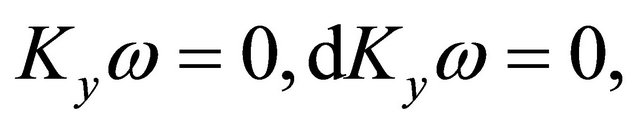

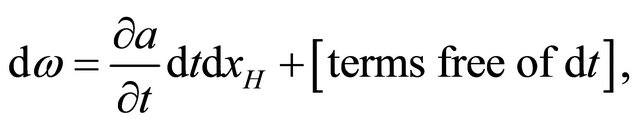(17)

(18)

But 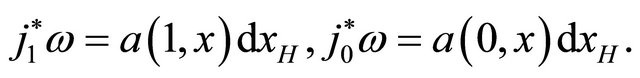So the formula is valid .

Case 2.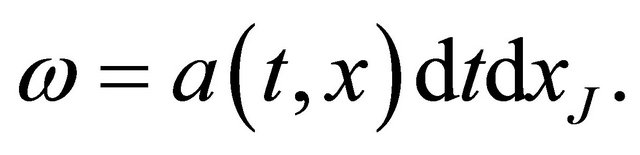

First notice 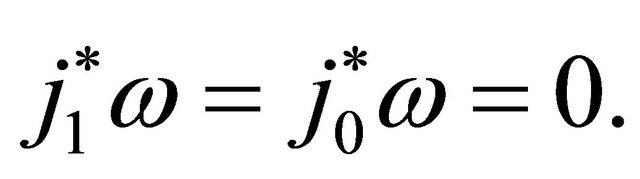Next we have

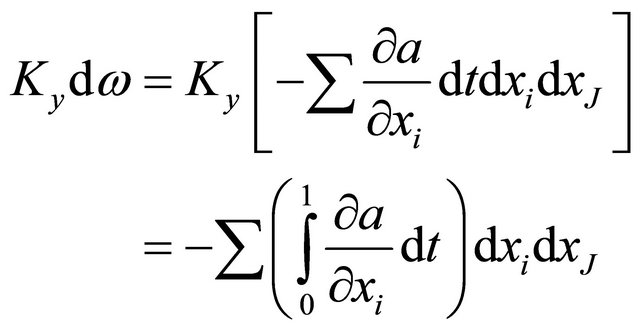, (19)

(20)

So the formula works, again.

We can easily get the following conclusion:

Lemma 3.1. For the mapping, the boundary conditions may be interpreted in terms of the as follows:

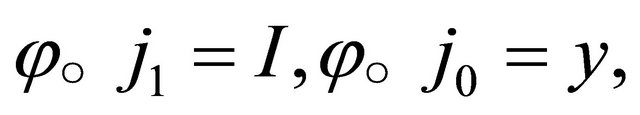(21)

if U is deformable to the point y.

For an (l +1)-form ω on U we have

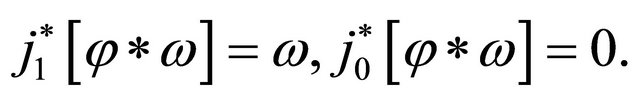(22)

Now we state and prove the main result.

Theorem 3.1. Assume U is a domain in which can be deformed to every point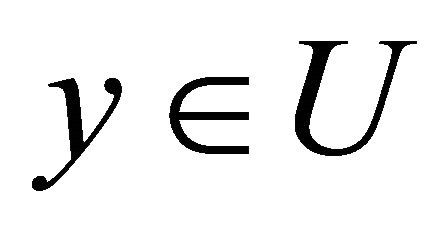. Let ω be an (l + 1)-form on U. Then there is

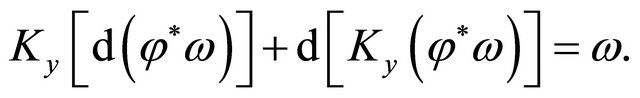(23)

Proof: We only substitute in the above formula of Lemma 3.1. And with Equation (22), we finish the proof.

Thus we finish the extension. It’s interesting to see if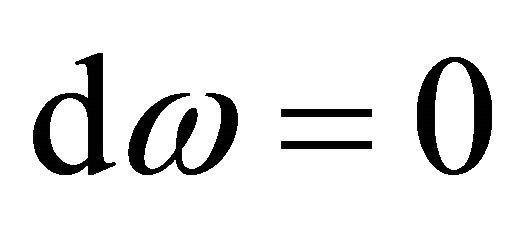, then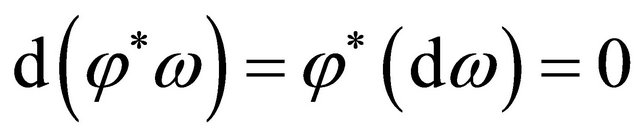. Hence with the formula above we hav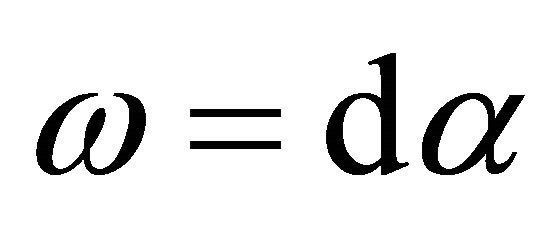e where This is just the generalization of the converse of the Poincar’e Lemma in [3], which shows that closed form is an exact form.

Corollary 3.1. Assume U is a domain in 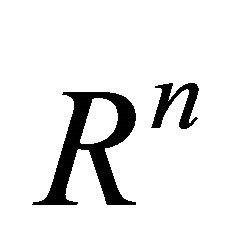which can be deformed to every point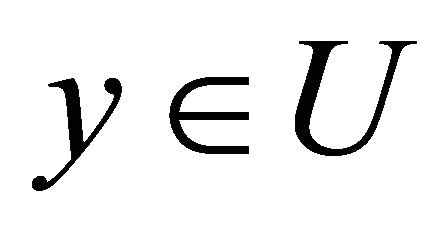. If ω is a closed (l+1)-form on U, then it is an exact form. Then we can construct a homotopy operator 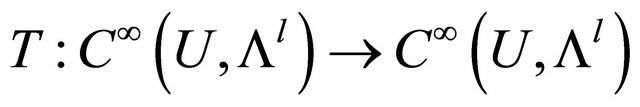by averaging 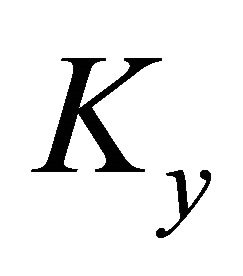over all points:

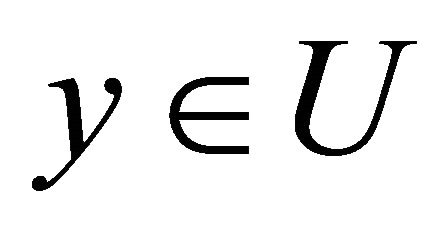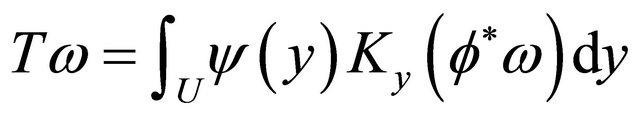(24)

where 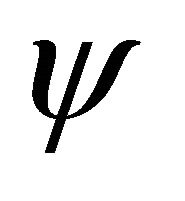in 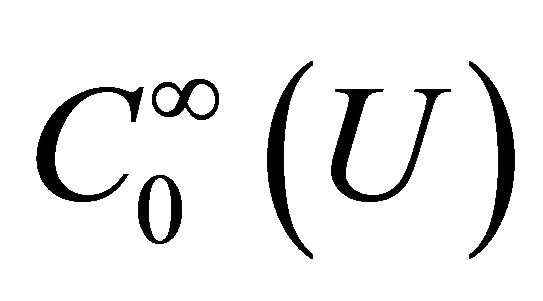is normalized so that

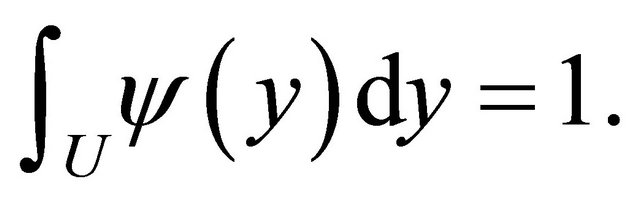It is obvious that the main result of this article remains valid for the operator T:

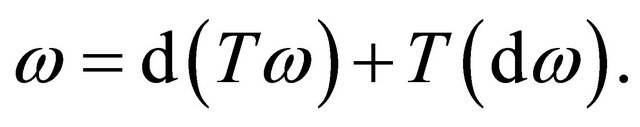(25)

We begin with the equation of Lemma 3.1

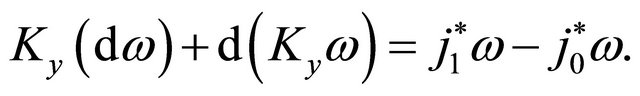(26)

Multiplying 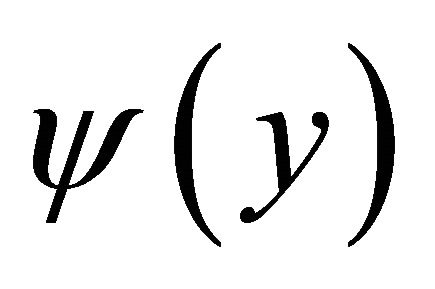to it and integraling on U, we have

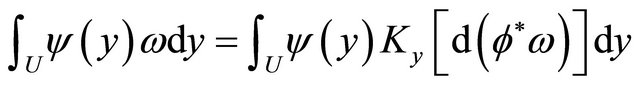(27)

Then with 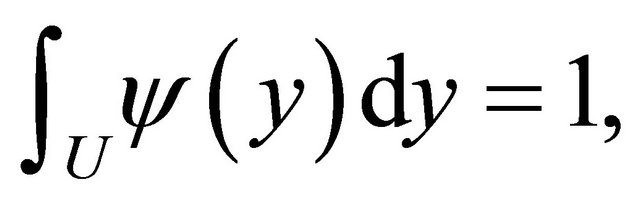we obtain

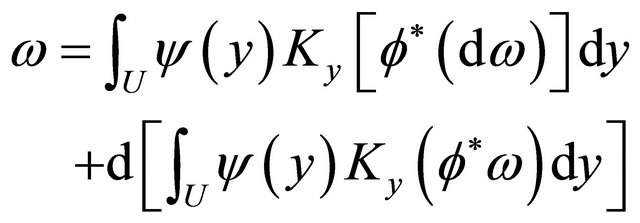(28)

which yields the above formula.

4. Conclusion

We have obtained an extension of the Poincar’e Lemma for differential forms in a bounded, convex domain in Rⁿ to a more general domain. Then we have extended the homotopy operator T to the domain defromed to every point of itself. So all of the conclusions about the homotopy operator T can be extended to the deformed domain.

5. Acknowledgements

The research of the author was supported by the Fundamental Research (2010) of NUDT (NO. JC10-02-02).

REFERENCES