Advances in Linear Algebra & Matrix Theory
Vol.4 No.2(2014), Article
ID:45920,4
pages
DOI:10.4236/alamt.2014.42007
A Further Result on the Cyclic Subspace
Huailei Wang
State Key Laboratory of Mechanics and Control for Mechanical Structures, Nanjing University of Aeronautics and Astronautics, Nanjing, China
Email: whlay@nuaa.edu.cn
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 28 February 2014; revised 28 March 2014; accepted 4 April 2014
ABSTRACT
Based on the geometric theories of vector space, a Cross-Identity theorem is proved for the relationship between the power kernels and power images of linear map  on its cyclic subspace. By this result, a new approach of proof is found for the fact that a square matrix with only one eigenvalue and one-dimensional eigenspace is similar to a Jordan block matrix.
on its cyclic subspace. By this result, a new approach of proof is found for the fact that a square matrix with only one eigenvalue and one-dimensional eigenspace is similar to a Jordan block matrix.
Keywords:Power Kernel, Power Image, Cyclic Subspace, Jordan Block Matrix, Linear Map

1. Introduction
Linear algebra has a wide range of application in most scientific and technological areas. As a fundamental part, the theory of vector space and linear map has developed to be a nearly perfect subject since nineteenth century. In the viewpoint of the author, when applying the theory to diverse problems, the more the detailed aspects of the knowledge one is in possession of, the more proficient one will become in dealing with those related problems. For example, in one of the excellent dynamical system monographs “Differential equations, Dynamical Systems, and an Introduction to Chaos” [1] , the authors put a separate chapter named “Higher Dimensional Linear Algebra” to help the readers recall some relevant linear algebra knowledge needed for the analysis of differential equations and dynamical systems, despite so many linear algebra monographs available for reference, such as [2] -[8] to name a few. Although it is just a brief review of higher dimensional linear algebra, the authors presented therein a distinct method to prove that a ![]() matrix can be transformed by a similarity transformation to a Jordan block matrix when it has only one eigenvalue and one-dimensional eigenspace. The essence of the method resides in a subtle analysis of the dimension of the kernel and the image of the matrix. Motivated by this method, this study is intended to generalize the results to the
matrix can be transformed by a similarity transformation to a Jordan block matrix when it has only one eigenvalue and one-dimensional eigenspace. The essence of the method resides in a subtle analysis of the dimension of the kernel and the image of the matrix. Motivated by this method, this study is intended to generalize the results to the  matrix. For this purpose, it is found that it is necessary to gain a deep insight into some geometric properties of the
matrix. For this purpose, it is found that it is necessary to gain a deep insight into some geometric properties of the 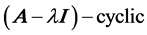 subspace, which finally leads to a more specific relationship discovered between the power-m kernel and the power-m image of linear map
subspace, which finally leads to a more specific relationship discovered between the power-m kernel and the power-m image of linear map![]() , which is reffered to as the Cross-Identity theorem below. As a corollary of this theorem, we proved the fact that a
, which is reffered to as the Cross-Identity theorem below. As a corollary of this theorem, we proved the fact that a  square matrix with only one eigenvalue and one eigenvector is similar to a Jordan block matrix.
square matrix with only one eigenvalue and one eigenvector is similar to a Jordan block matrix.
The paper is organized as follows. In Section 2, some basic facts will be recalled as preliminaries for the good understanding of the work. Section 3 presents the main results of this paper with some lemmas preceding the Cross-Identity theorem. Some conclusions are drawn finally in Section 4.
2. Preliminaries
Let ![]() be a n-dimensional vector space over the complex numbers, and
be a n-dimensional vector space over the complex numbers, and  be the set of all linear maps mapping the vector space
be the set of all linear maps mapping the vector space ![]() into itself, and let
into itself, and let ![]() and
and ![]() denote the kernel (null space) and the image (range) of a linear map
denote the kernel (null space) and the image (range) of a linear map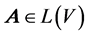 , respectively, then it is well known that if the characteristic polynomial of
, respectively, then it is well known that if the characteristic polynomial of ![]() is factorized as
is factorized as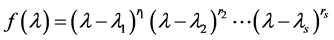 ,
,  being its distinct eigenvalues, then the vector space
being its distinct eigenvalues, then the vector space ![]() can be decomposed into the direct sum of some subspaces, i.e.
can be decomposed into the direct sum of some subspaces, i.e.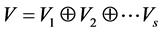 , where
, where  with
with  denoting the identity map. Moreover, it can also be proved by using the primary decomposition that each of the above subspace
denoting the identity map. Moreover, it can also be proved by using the primary decomposition that each of the above subspace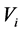 , and hence the whole vector space
, and hence the whole vector space![]() , can be further expressed as a direct sum of
, can be further expressed as a direct sum of 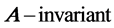 cyclic subspaces [3] . Because the transformation matrix of a linear map under a cyclic basis takes on a Jordan normal form, the above decomposition theories lead straightforward to a geometric approach of proof for the fact that any square matrix
cyclic subspaces [3] . Because the transformation matrix of a linear map under a cyclic basis takes on a Jordan normal form, the above decomposition theories lead straightforward to a geometric approach of proof for the fact that any square matrix ![]() can be brought into Jordan normal form through a similarity transformation with a change-of-basis matrix (another way leading to this result is through the elementary divisor theory [7] ).
can be brought into Jordan normal form through a similarity transformation with a change-of-basis matrix (another way leading to this result is through the elementary divisor theory [7] ).
From the above viewpoint, the cyclic subspace of a vector space shall be an important concept in the field of linear algebra. For the convenience of reference, some preliminary concepts are presented below, for which one can also refer to [3] .
Definition 2.1 Cyclic vector Let 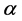 be a complex number, let
be a complex number, let![]() ,
, ![]() , then
, then 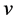 is called
is called  if there exists an integer
if there exists an integer  such that
such that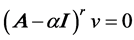 . The smallest positive integer
. The smallest positive integer  having this property will then be called a period of
having this property will then be called a period of 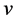 relative to
relative to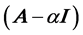 .
.
Definition 2.2 Cyclic space The vector space ![]() will be called cyclic if there exists some number
will be called cyclic if there exists some number  and an element which is
and an element which is  and
and 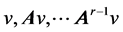 generate
generate![]() .
.
Theorem 2.3 if ![]() is
is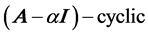 , with period
, with period , then
, then 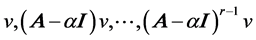 are linearly independent.
are linearly independent.
Definition 2.4 Cyclic basis if ![]() is
is , with period
, with period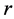 , then
, then 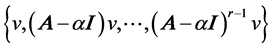 is called a cyclic basis or Jodan basis for the cyclic space
is called a cyclic basis or Jodan basis for the cyclic space ![]() it generates.
it generates.
Definition 2.5 Jordan block matrix A matrix is called a Jordan block matrix if it has the same number ![]() on the diagonal, 1 above the diagonal, and 0 everywhere else.
on the diagonal, 1 above the diagonal, and 0 everywhere else.
Theorem 2.6 Let ![]() be a linear map defined on a
be a linear map defined on a 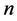 -dimensional cyclic space
-dimensional cyclic space![]() , then the associated matrix
, then the associated matrix 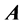 with respect to the cyclic basis
with respect to the cyclic basis 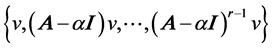 is equal to a Jordan block matrix.
is equal to a Jordan block matrix.
Hence, it has only one eigenvalue ![]() and one-dimensional eigenspace.
and one-dimensional eigenspace.
Definition 2.7 Fan and Fan basis By a fan of linear map A in vector space ![]() , we shall mean a sequence of subspaces
, we shall mean a sequence of subspaces  such that
such that  is contained in
is contained in  for each
for each , such that
, such that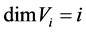 , and finally such that each
, and finally such that each 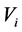 is
is . By a fan basis, we shall mean a basis
. By a fan basis, we shall mean a basis 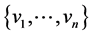 of
of ![]() such that
such that 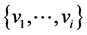 is a basis for
is a basis for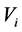 .
.
3. Cross-Identity Theorem
To state the results of this paper, some more notations need to be introduced. As is known, the customary eigenspace of a linear map 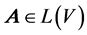 associated with eigenvalue
associated with eigenvalue ![]() is equivalent to
is equivalent to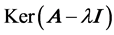 , and the corresponding generalized eigenspaces are the union set of
, and the corresponding generalized eigenspaces are the union set of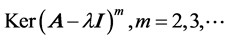 . For convenience, we refer to
. For convenience, we refer to 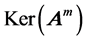 and
and 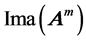 as power-m kernel and power-m image with respect to linear map
as power-m kernel and power-m image with respect to linear map ![]() , respectively. In this case, the customary eigenspace and the generalized eigenspaces associated with eigenvalue
, respectively. In this case, the customary eigenspace and the generalized eigenspaces associated with eigenvalue ![]() are the power-one kernel and the higher power kernels of linear map
are the power-one kernel and the higher power kernels of linear map![]() .
.
Since a vector space can be expressed as a direct sum of  cyclic subspaces, we only consider one of its
cyclic subspaces, we only consider one of its 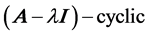 subspace, or without loss of generality, suppose
subspace, or without loss of generality, suppose ![]() entirely is a
entirely is a 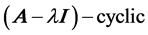 space hereafter. In this situation, according to Theorem 2.6,
space hereafter. In this situation, according to Theorem 2.6, ![]() has only one eigenvalue and one-dimensional eigensapce. In addition, according to the direct sum decomposition of the
has only one eigenvalue and one-dimensional eigensapce. In addition, according to the direct sum decomposition of the 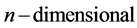 vector space, there shall be
vector space, there shall be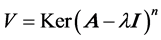 , which means
, which means ![]() is nilpotent on cyclic space
is nilpotent on cyclic space![]() . In what follows, we will show step by step that in this situation, there is a concise relationship between the corresponding power kernels and power images of linear map
. In what follows, we will show step by step that in this situation, there is a concise relationship between the corresponding power kernels and power images of linear map![]() . For simplicity, the following abbreviations of notations are introduced:
. For simplicity, the following abbreviations of notations are introduced:
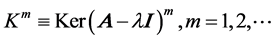

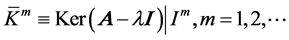
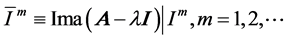
where 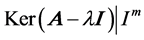 means the restricted eigenspace in subspace
means the restricted eigenspace in subspace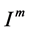 , and
, and 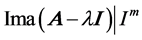 means the restricted image of
means the restricted image of ![]() on
on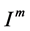 . In what follows, the power 1 will be omitted when
. In what follows, the power 1 will be omitted when![]() , i.e.
, i.e. ,
,  ,
,  ,
, . Then it is easy to verify that
. Then it is easy to verify that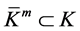 ,
, 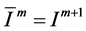 ,
,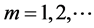 . The above analysis also readily yields that
. The above analysis also readily yields that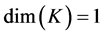 ,
,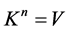 .
.
Now, it is ready to present some further results for a cyclic space as follows.
Lemma 3.1 If![]() , then
, then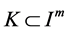 ,
,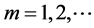 .
.
Proof Note that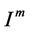 ,
,  are all
are all 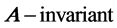 subspaces, then since
subspaces, then since ,
, ![]() must have an eigenvector in
must have an eigenvector in , which implies
, which implies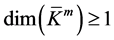 ,
,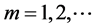 . Recall that
. Recall that 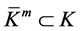 and
and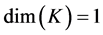 , it leads straightforward to
, it leads straightforward to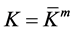 . Note
. Note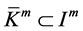 , then we have
, then we have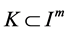 .
.
Lemma 3.2 If , then
, then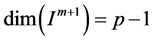 ,
,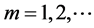 .
.
Proof  implies
implies![]() , then from Lemma 3.1 there will be
, then from Lemma 3.1 there will be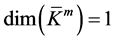 ,
, . Let
. Let , then it follows
, then it follows

which results in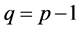 , i.e.
, i.e. .
.
From Lemma 3.2, one can see that for a cyclic subspace, the sequence of the dimensions of power images  decrease with step one, and hence, the sequence of dimensions of power kernels
decrease with step one, and hence, the sequence of dimensions of power kernels 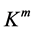 will increase with step one.
will increase with step one.
Corollary 3.3 .
.
Proof Note that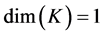 , there must be
, there must be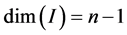 . By Lemma 3.2, it follows that
. By Lemma 3.2, it follows that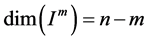 . Since
. Since , then we have
, then we have .
.
Theorem 3.4 (Cross-Identity Theorem) The power kernels and power images of linear map ![]() on a cyclic space have the following Cross-Identity relationship, i.e.
on a cyclic space have the following Cross-Identity relationship, i.e.
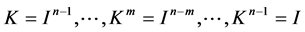
Proof By Corollary 3.3, we can know readily that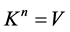 ,
,![]() . Moreover, according to the definition of
. Moreover, according to the definition of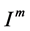 ,
, 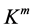 , it is easy to verify the following inclusion sequence.
, it is easy to verify the following inclusion sequence.

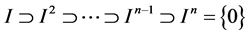
We give the proof in what follows by two steps. The first step is to prove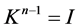 . Since
. Since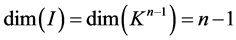 , so for
, so for , there is a
, there is a ![]() such that
such that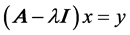 , which yields
, which yields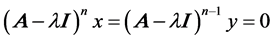 . Hence,
. Hence, 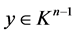 , and therefore
, and therefore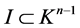 . Because
. Because  and
and 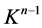 have the same dimension, there must be
have the same dimension, there must be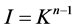 . Then we have
. Then we have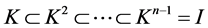 . Next step is to prove
. Next step is to prove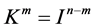 ,
,![]() . For
. For , we have
, we have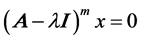 . Since
. Since![]() , then
, then . Hence, there must exist an
. Hence, there must exist an 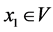 such that
such that 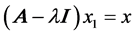 with
with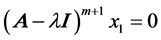 . Since
. Since![]() , then
, then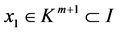 , which means there must exit an
, which means there must exit an  such that
such that 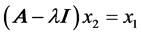 with
with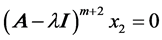 . Carrying on with this procedure, one can find an
. Carrying on with this procedure, one can find an 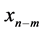 such that
such that  with
with  . Now it can be deduced from above that
. Now it can be deduced from above that , i.e.
, i.e. , which implies
, which implies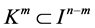 . According to Corollary 3.3,
. According to Corollary 3.3,  , thus, we can readily contend that
, thus, we can readily contend that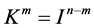 .
.
Corollary 3.5 Suppose matrix 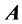 has only one eigenvalue, and the corresponding eigenspace v is one dimensional, then there must exist a transformation matrix
has only one eigenvalue, and the corresponding eigenspace v is one dimensional, then there must exist a transformation matrix 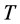 such that
such that 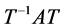 is a Jordan block matrix.
is a Jordan block matrix.
Proof Let matrix 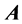 be the associated matrix of a linear map
be the associated matrix of a linear map 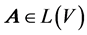 under a basis
under a basis . Since
. Since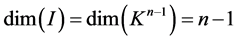 , then there must be an
, then there must be an ![]() such that
such that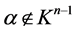 , i.e.
, i.e. . Let
. Let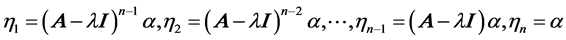 , then it is easy to verify that
, then it is easy to verify that  constitutes a fan basis of
constitutes a fan basis of![]() . Thus, it is available to define an invertible linear transformation
. Thus, it is available to define an invertible linear transformation 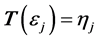 with an invertible transformation matrix T, such that
with an invertible transformation matrix T, such that
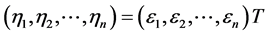
Notice that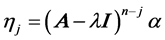 , we have
, we have , i.e.
, i.e.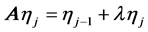 . Then,
. Then, . From the above transformation we can contend that
. From the above transformation we can contend that 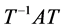 is a Jordan block matrix with the following form
is a Jordan block matrix with the following form
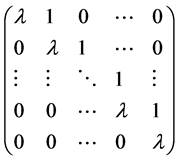
4. Conclusion
This paper studies some special properties of cyclic subspaces. Although it is well known that the dimensions of the power kernels of a linear map on a vector space are decreasing, and the corresponding power images are increasing, i.e. 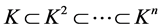 and
and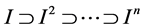 , we show in this paper that for a cyclic subspace, the sequence of the dimensions of power kernels increases with step one, and the sequence of dimensions of power images decreases with step one. Besides, we find a Cross-Identity relationship between the power kernels and the power images, which is peculiar to cyclic subspaces. Another contribution of this paper is that we find a new way, by the application of the cross-identity theorem, to prove that a square matrix with only one eigenvalue and one-dimensional eigenspace is similar to a Jordan block matrix.
, we show in this paper that for a cyclic subspace, the sequence of the dimensions of power kernels increases with step one, and the sequence of dimensions of power images decreases with step one. Besides, we find a Cross-Identity relationship between the power kernels and the power images, which is peculiar to cyclic subspaces. Another contribution of this paper is that we find a new way, by the application of the cross-identity theorem, to prove that a square matrix with only one eigenvalue and one-dimensional eigenspace is similar to a Jordan block matrix.
Acknowledgements
This work is supported by the National Natural Science Foundation of China (Grant No. 11172126). We also would like to thank the referees for their comments and suggestions.
References
- Hirsch, M.W., Smale, S. and Devaney R.L. (2004) Differential Equations, Dynamical Systems, and an Introduction to Chaos. 2nd Edition, Elsevier Academic Press, San Diego.
- Greub, W.H. (1967) Linear Algebra. 3rd Edition, Springer, Berlin.
- Lancaster, P. and Tismenetsky, M. (1985) The Theory of Matrices: With Applications. Academic Press Inc., San Diego.
- Lang, S. (1987) Linear Algebra. 3rd Edition, Springer, New York. http://dx.doi.org/10.1007/978-1-4757-1949-9
- Axler, S. (1997) Linear Algebra Done Right. Springer, New York. http://dx.doi.org/10.1007/b97662
- Lax, P.D. (2007) Linear Algebra and Its Applications. 2nd Edition, John Wiley & Sons Inc, Hoboken, New Jersey.
- Roman, S. (2008) Advanced Linear Algebra. 3rd Edition, Springer, New York.
- Xu, Y.C. (2008) Linear Algebra and Matrix Theory. 2nd Edition, High Education Press, Beijing (in Chinese).

