American Journal of Analytical Chemistry
Vol.08 No.07(2017), Article ID:77574,21 pages
10.4236/ajac.2017.87036
Reliable Method for Steady-State Concentrations and Current over the Diagnostic Biosensor Transducers
Kurunatha Perumal Thevar Preethi1*, Velmurgan Meena2, Rajaram Poovazhaki1*
1Department of Mathematics, E.M.G. Yadava Women’s College, Madurai, India
2Department of Mathematics, Madurai Kamaraj University Constitutional College, Madurai, India

Copyright © 2017 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: April 19, 2017; Accepted: July 9, 2017; Published: July 12, 2017
ABSTRACT
A mathematical modelling of diagnostic biosensors system at three basic types of enzyme kinetics is discussed in the presence of diffusion. Enzyme kinetics is adopted to be first order, Michaelis-Menten and ping-pong mechanism. In this paper, approximate analytical solutions are obtained for the non-linear equations under steady-state conditions by using the new Homotopy perturbation method. Simple and closed forms of analytical expressions for concentrations of substrate, product and co-substrate and corresponding current response have been derived for all possible values of parameters. Furthermore, the numerical simulation of the problem is also reported here by using Matlab program. Good agreement between analytical and numerical results is noted.
Keywords:
Diagnostic Biosensor, Bio Fuel, Enzyme, Kinetic, Non Linear Equations, Reaction/Diffusion Equation, Homotopy Perturbation Method

1. Introduction
A biosensor is an analytical device used for the detection of an analyte that combines a biological component with a physicochemical detector [1] [2] . The earlier biosensors were catalytic systems that integrated especially enzymes with transducers that converted the biological response into an electronic signal. The next generation of biosensors, took advantage of different biological elements, such as antibodies, receptors (natural or synthetic), or nucleic acids [3] [4] .
Biosensors for environmental application include the detection of harmful bacteria or pesticides in air, water, or food. New technologies are likely to encompass all-printed systems capitalising on the printed electronics revolution and systems with high compatibility with future mobile technology such as tablets and 4G phones [5] .
Rangelova et al. [6] [7] [8] described the models in biosensors and investigated the influence of the diffusion and kinetic parameters on the response of the biosensor. Tothil et al., [9] deals with the recent developments in biosensors and their potential use in the agricultural diagnostic market. Mishra et al. [10] reviewed various cancer biomarkers in saliva and compared the biomarkers efficacy with traditional diagnostics and state-of-the-art bioelectronics. Cortina et al. [11] presented the development and validation of a portable, robust and inexpensive electrochemical magnetic biosensor.
Lawal et al. [12] summarized the fabrication of carbon nanotubes-based electrochemical biosensors. They also discussed the synthesis, along with the application of carbon nanotubes to the assembly of carbon nanotube-based electrochemical sensors, its analytical performance and future expectations. Recently Gruhl et al. [13] described the latest applications of biosensors in diagnostic applications. In this paper the current state and future trends of biosensors are presented. Also Mascini et al. [3] reviewed the application of biosensor sin medical diagnostics, taking into account several crucial features.
The numerical method of solving the system of partial differential equations is to make calculation at all intervals of substrates concentration and at different diffusion and enzymatic reaction rates. The diffusion equations [14] , containing a nonlinear term related to the enzymatic reaction, are carried out using the implicit difference scheme [15] . In recent years, analytical solutions are reported for various types of biosensors [16] [17] [18] [19] . The analytical results of diagnostic biosensor are relevant because their solutions describe important applications such as bioreactors and biofuel cells, among others [20] [21] .
To the researcher’s knowledge no rigorous analytical solution of substrate concentration product with concentration profiles co-substrate concentration and corresponding current response has been derived for all possible values of parameters under steady-state conditions [22] . The purpose of this communication is to derive approximate analytical expressions for the steady-state concentrations and current over the diagnostic of biosensor transducers for first order, Michaelis-Menten and ping-pong kinetics using Homotopy perturbation method.
2. Mathematical Description of the Boundary Value Problem
Only biosensors systems will be investigated in the active membrane, because it is known that the concentrations of substrate , Product
, Product 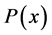 and co-substrate
and co-substrate 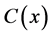 in other two membranes are changed linearly. Biosensors are function under diffusion control. It is assumed that the electrode has symmetrical geometry and the enzyme is homogeneously distributed in the active membrane. The diffusion is one dimensional in space and is described with the second Fick’s law. The two parameters diagnostic biosensor transducers are based on oxygen electrode. The steady-state reaction-diffusion equation for biosensor systems in the dynamic mode has the following form [22] :
in other two membranes are changed linearly. Biosensors are function under diffusion control. It is assumed that the electrode has symmetrical geometry and the enzyme is homogeneously distributed in the active membrane. The diffusion is one dimensional in space and is described with the second Fick’s law. The two parameters diagnostic biosensor transducers are based on oxygen electrode. The steady-state reaction-diffusion equation for biosensor systems in the dynamic mode has the following form [22] :
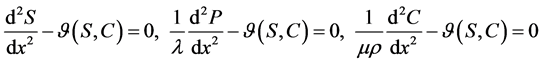 (1)
(1)
The non-dimensional coordinates, variables and parameters are as follows:
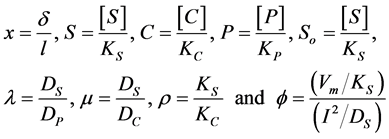 (1a)
(1a)
where 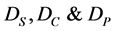 are diffusion coefficients for substrate, co-substrate and product.
are diffusion coefficients for substrate, co-substrate and product.  denotes the reaction constant for concentration profiles (
denotes the reaction constant for concentration profiles (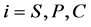 ), respectively.
), respectively.  is the enzyme rate and
is the enzyme rate and  represents the coordinate distance. The diagnosis of the biosensor system depends on the enzyme kinetics and the enzyme reaction as well as on the basic transducer. The kinetics is distinguished in to three kinds:
represents the coordinate distance. The diagnosis of the biosensor system depends on the enzyme kinetics and the enzyme reaction as well as on the basic transducer. The kinetics is distinguished in to three kinds:
First order kinetic:
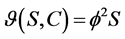 (2)
(2)
Michaelis-Menten kinetic:
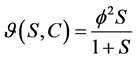 (3)
(3)
Two substrateping-pong kinetic:
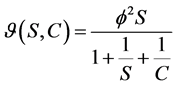 (4)
(4)
The three types of biosensors can be described with the following system of differential equations:
Equations (5)-(13) are subjected to the following boundary conditions:
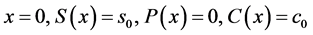
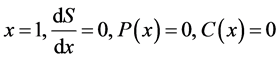 (14)
(14)
where 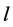 represents the thickness of active membrane,
represents the thickness of active membrane, 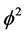 is the Thiele Module,
is the Thiele Module, 





where 


Analytical Solutions of Concentrations of Substrate, Product and Co-Substrate under Steady-State Condition Using the New Homotopy Perturbation Method
Recently, many authors have applied the HPM to solve the various non-linear problem in engineering sciences [23] - [28] . This method is a combination of Homotopy in topology and classic perturbation techniques. The HPM has uniqueness in its applicability, accuracy, and efficiency. Recently, a new approach of HPM with zeroth iteration has been applied to solve the nonlinear problem. In this work, a new approach to Homotopy perturbation method is used (Appen- dix A and Appendix B) to solve the nonlinear differential Equations (5)-(13). Using this method, the analytical expression of the concentration of substrate


The first order kinetic Equations (18)-(20) represent the simple and closed form of analytical expressions of concentrations of substrate, product and co- substrate for all possible values of the parameters. By using Equations (5)-(7) with boundary conditions (14), the following relation is also obtained:
First order kinetic
The Michaelis?Menten kinetic Equations (24)-(26) represent the simple and closed form of analytical expressions of concentrations of substrate, product and co-substrate for all possible values of the parameters. By using Equations (8)-(10) with boundary conditions (14), the following relation is also obtained:
Michaelis-Menten kinetic:
The Ping pong kinetic: Equations (30)-(32) represent the simple and closed forms of analytical expressions of concentrations of substrate, product and co- substrate for all possible values of the parameters. By using Equations (11)-(13) with boundary conditions (14), the following relation is also obtained:
Ping pong kinetic:
where

3. Numerical Simulation
The system of non-linear differential Equations (5)-(13) with boundary conditions (14) have been solved numerically using MATLAB software. A MATLAB script pdex4 is provided in Appendix C. In Figure 4, Tables 1-3 the numerical solutions are compared with the analytical results. The maximum average relative error between our analytical and numerical result is 0.94% for first order kinetic, 0.91% for Michaelis?Menten kinetic and 1.54% for Ping pong kinetic.
4. Results and Discussion
The dinensonless non-linear differential equations are solved using a new Homotopy perturbation method. Equations (18)-(20), (24)-(26) and (30)-(32) re- present the analytical expression of the concentrations of substrate, product and co-substrate for various values of Thiele modulus 
Table 1. Comparison of dimensionless concentrations 

Table 2. Comparison of dimensionless concentrations 

Table 3. Comparison of dimensionless concentrations 

Figures 1-3 show the plots of all the concentrations versus dimensionless distance 



The substrate concentration 




Figure 4 focuses the concentration on the first-order kinetics, Michaelis- Menten kinetics, and ping-pong kinetic mechanism of the substrate


Figure 5 represents the concentration of the substrate, product and co-sub- strate vursus distance for the first-order kinetics, Michaelis?Menten kinetics, and ping-pong kinetic mechanism for particular values of parameters. From this figure, it is inferred that the concentration of the ping-pong kinetics largely corresponds to the other two mechanisms. But for the co substrate, the concentration does not show much difference. From these Figure, it is concluded that the dimensionless concentration of substrate and co-substrateis greater for the Ping-Pong than the first order and M-M kinetics.
Figure 6 and Figure 7 represent the dimensionless current profiles of product and co-substrate for various values of dimensionless parameters. The current depends on the product and co-substrate gradient at the electrode surface. 




4. Conclusion
In this work, a mathematical model that describes the steady-state response of a two parameters diagnostic of biosensor is discussed. Anew Homotopy perturbation method is employed to solve the system of steady-state non-linear differential equations for three types of kinetics. Analytical expressions corresponding to substrate, product and co-substrate concentrations are derived as the function of dimensionless parameters. For all different concentrations, the analytical results match well with the simulated results. The analytical results provided in this work are useful to understand the behaviour of the system. The extension



Figure 1. (a)-(f) Plot of dimensionless concentrations of the substrate









Figure 2. Plot of dimensionless concentrations of the substrate









Figure 3. (a)-(f) Plot of dimensionless concentrations of the substrate









Figure 4. Concentration of substrate





Figure 5. Concentration of substrate





Figure 6. Generalised graph of the dimensionless current for product 

Figure 7. Generalised graph of the dimensionless current for co-substrate product 

of the procedure to other systems nonlinear equation in various type of biosensor seems to be possible.
Cite this paper
Preethi, K.P.T., Meena, V. and Poovazhaki, R. (2017) Reliable Method for Steady-State Concentrations and Current over the Diagnostic Bio- sensor Transducers. American Journal of Analytical Chemistry, 8, 493-513. https://doi.org/10.4236/ajac.2017.87036
References
- 1. Thevenot, D.R., Toth, K., Durst, R.A. and Wilson, G.S. (2001) Electrochemical Biosensors: Recommended Definitions and Classification. Biosensors and Bioelectronics, 16, 121-131.
- 2. Newman, J.D., Tigwell, L.J., Turner, A.P.F. and Warner, P.J. (2004) Biosensors—A Clearer View. Cranfield University Publication.
- 3. Mascini, M. and Tombelli, S. (2008) Biosensors for Biomarkers in Medical Diagnostics. Biomarkers, 13, 637-657.
https://doi.org/10.1080/13547500802645905 - 4. Zhang, Y., Yang, D., Weng, L. and Wang, L. (2013) Early Lung Cancer Diagnosis by Biosensors. International Journal of Molecular Sciences, 14, 15479-15509.
https://doi.org/10.3390/ijms140815479 - 5. Turner, A.P. (2013) Biosensors: Sense and Sensibility. Chemical Society Review, 42, 3184-3196.
- 6. Rangelova, V., Katsarova, P. and Iliev, K.J. (2007) Influence of Parameters over Biosensors Response in Dynamic Mode at Different Enzyme Kinetic. Annals of the Faculty of Engineering Hunedoara—Journal of Engineering, 5, 105-112.
- 7. Rangelova, V. (2006) Modeling Amperometric Biosensor with Cyclic Reaction. Annals of the Faculty of Engineering Hunedoara—Journal of Engineering, 5, 116-122.
- 8. Rangelova, V., Pandelova, A. and Stoiyanov, N. (2011) Inhibitor Multienzyme Biosensor System in Dynamic Mode—Phosphate Measurement. Annals of the Faculty of Engineering Hunedoara—Journal of Engineering, 9, 83-86.
- 9. Tothill, I.E. (2001) Biosensors Developments and Potential Applications in the Agricultural Diagnosis Sector. Computers and Electronics in Agriculture, 30, 205-218.
- 10. Mishra, S., Saadat, D., Kwon, O., Lee, Y., Choi, W.S., Kim, J.H. and Yeo, W.H. (2016) Recent Advances in Salivary Cancer Diagnostics Enabled by Biosensors and Bioelectronics. Biosensors and Bioelectronics, 81, 181-197.
- 11. Cortina, M.E., Melli, L.J., Roberti, M., Mass, M., Longinotti, G., Tropea, S., Lloret, P., Serantes, D.A.R., Salomón, F., Lloret, M., Caillava, A.J., Restuccia, S., Altcheh, J., Buscaglia, C.A., Malatto, L., Ugalde, J.E., Fraigi, L., Moina, C., Ybarra, G., Ciocchini, A.E. and Comerci, D.J. (2016) Electrochemical Magnetic Microbeads-Based Biosensor for Point-of-Care Sero-Diagnosis of Infectious Diseases. Biosensors and Bioelectronics, 80, 24-33.
- 12. Lawal, A.T. (2016) Synthesis and Utilization of Carbon Nanotubes for Fabrication of Electrochemical Biosensors. Materials Research Bulletin, 73, 308-350.
- 13. Gruhl, F.J., Rapp, B.E. and Lange, K. (2013) Biosensors for Diagnostic Applications. In: Seitz, H. and Schumacher, S., Eds., Molecular Diagnostics. Advances in Biochemical Engineering/Biotechnology, Vol. 133, Springer, Berlin, Heidelberg, 115-148.
https://doi.org/10.1007/10_2011_130 - 14. Baronas, R., Ivanauskas, F. and Kulys, J. (1999) Modelling a Biosensor Based on the Heterogeneous Microreactor. Journal of Mathematical Chemistry, 25, 245-252.
https://doi.org/10.1023/A:1019192618843 - 15. Ames, W.F. (1977) Numerical Methods for Partial Differential Equations. 2nd Edition, Academic Press, New York.
- 16. Meena, A. and Rajendran, L. (2010) Mathematicalmodeling of Amperometric and Potentiometric Biosensors and System of Nonlinear Equations—Homotopy Perturbation Approach. Journal of Electroanalytical Chemistry, 644, 50-59.
- 17. Loghambal, S. and Rajendran, L. (2011) Mathematical Modeling in Amperometric Oxidase Enzyme-Membrane Electrodes. Journal of Membrane Science, 373, 20-28.
- 18. Manimozhi, P., Subbiah, A. and Rajendran, L. (2010) Solution of Steady-State Substrate Concentration in the Action of Biosensor Response at Mixed Enzyme Kinetics. Sensors and Actuators B: Chemical, 147, 290-297.
- 19. Venugopal, K., Eswari, A. and Rajendran, L. (2011) Mathematical Model for Steady State Current at PPO-Modified Micro-Cylinder Biosensors. Journal of Biomedical Science and Engineering, 4, 631-641.
https://doi.org/10.4236/jbise.2011.49079 - 20. Kirthiga, O.M. and Rajendran, L. (2015) Approximate Analytical Solution for Non-Linear Reaction Diffusion Equations in a Mono-Enzymatic Biosensor Involving Michaelis-Menten Kinetics. Journal of Electroanalytical Chemistry, 751, 119-127.
- 21. Saravanakumara, K., Rajendrana, L. and Sangaranarayananb, M.V. (2015) Current-Potential Response and Concentration Profiles of Redoxpolymer-Mediated Enzyme Catalysis in Biofuel Cells—Estimation of Michaelis-Menten Constants. Chemical Physics Letters, 621, 117-123.
- 22. Katzarova, P., Rangelova, V. and Kuneva, S. (2006) Two Parameters Diagnostic of Biosensor Transducers. Biotechnology & Biotechnological Equipment, 20, 190-194.
https://doi.org/10.1080/13102818.2006.10817331 - 23. Ozis, T. and Yildirim, A. (2007) A Comparative Study of He’s Homotopy Perturbation Method for Determining Frequency-Amplitude Relation of a Nonlinear Oscillator with Discontinuities. International Journal of Nonlinear Sciences and Numerical Simulation, 8, 243-248.
https://doi.org/10.1515/IJNSNS.2007.8.2.243 - 24. Mousa, M.M. and Ragab, S.F. (2008) Application of the Homotopy Perturbation Method to Linear and Nonlinear Schrodinger Equations. Zeitschrift fur Naturforschung, 63, 140-144.
- 25. He, J.H. (1999) Homotopy Perturbation Technique. Computer Methods in Applied Mechanics and Engineering, 178, 257-262.
- 26. Rajendran, L. and Anitha, S. (2013) Reply to “Comments on Analytical Solution of Amperometric Enzymatic Reactions Based on HPM”. Electrochimica Acta, 102, 474-476.
- 27. Meena, V., Indira, K., Kumar, S. and Rajendran, L. (2014) A New Mathematical Model for Effectiveness Factors in Biofilm under Toxic Conditions. Alexandria Engineering Journal, 53, 917-928.
- 28. Meena, A. and Rajendran, L. (2010) Mathematical Modeling of Amperometric and Potentiometric Biosensors and System of Nonlinear Equations—Homotopy Perturbation Approach. Journal of Electroanalytical Chemistry, 644, 50-59.
Appendix A
Approximate analytical solutions for Equations (8)-(10) (Michaelis-Men- ten kinetic) using HPM:
In order to solve Equation (8-10) by means of the new HPM, first the Zeroth order deformation equation is constructed.



The approximate solutions of Equations (A1), (A2) and (A3) are as follows

Substituting (A4) in Equation (A1) and equating the like powers of p, we get


Substituting (A4) in Equation (A2) and equating the like powers of p, we get


Substituting (A4) in Equation (A3) and equating the like powers of p, we get


The boundary conditions in Equation (14) becomes

and

Now by applying the boundary conditions (A11) in (A5), (A7) and (A9), we get



Substituting the values of 




Adding Equations (A13) and (A16), we get Equation (24) in the text. Similarly, Equation (25) and Equation (26) are got in the text.
Appendix B
Approximate analytical solutions for Equations (11-13) (ping-pong kinetic) using HPM:
In order to solve Equations (11-13) by means of the new HPM, first the Zeroth order deformation equation is constructed.



The approximate solutions of Equations (B1), (B2) and (B3) are as follows

Substituting (B4) in Equations (B1) and equating the like powers of p, we get


Substituting (B4) in Equation (B2) and equating the like powers of p, we get


Substituting (B4) in Equation (B3) and equating the like powers of p, we get


The boundary conditions in Equation (14) becomes

and

Now by applying the boundary conditions (B11) in (B5), (B7) and (B9), we get



Substituting the values of 




Adding Equations (B13) and (B16), we get Equation (30) in the text. Similarly, Equation (31) and Equation (32) are got in the text.
Appendix C
Scilab/Matlab program for the numerical solution of the system of non- linear Equations (5-13).
function pdex4
m = 0;
x = linspace(0,1);
t=linspace(0,100000);
sol = pdepe(m,@pdex4pde,@pdex4ic,@pdex4bc,x,t);
u1 = sol(:,:,1);
u2 = sol(:,:,2);
u3 = sol(:,:,3);
figure
plot(x,u1(end,:))
title('u1(x,t)')
xlabel('Distance x')
ylabel('u1(x,2)')
%------------------------------------------------------------------
figure
plot(x,u2(end,:))
title('u2(x,t)')
xlabel('Distance x')
ylabel('u2(x,2)')
% --------------------------------------------------------------
figure
plot(x,u3(end,:))
title('u3(x,t)')
xlabel('Distance x')
ylabel('u3(x,2)')
%--------------------------------------------------------------
function [c,f,s] = pdex4pde(x,t,u,DuDx)
c = [1; 1; 1];
f = [1; 1; 1] .* DuDx;
l=0.1;mu=0.5;q=1;p=5;
F=-q^2*u(1);
F1=l*q^2*u(1);
F2=-mu*p*q^2*u(1);
s=[F; F1; F2];
% --------------------------------------------------------------
function u0 = pdex4ic(x);
u0 = [1; 1; 1];
% --------------------------------------------------------------
function [pl,ql,pr,qr]=pdex4bc(xl,ul,xr,ur,t)
pl = [ul(1)-1;ul(2)-0;ul(3)-1];
ql = [0; 0; 0];
pr = [0; ur(2)-0;ur(3)-0];
qr = [1;0; 0];
Nomenclature
Symbol


















Greek symbols






Subscripts



















