American Journal of Analytical Chemistry
Vol.06 No.04(2015), Article ID:54483,11 pages
10.4236/ajac.2015.64027
The True Value of a Sample Composition Is There
Hong Yi1, Wei Yi2
1Division of Metrology in Chemistry, National Institute of Metrology, Beijing, China
2Department of Biology, New York University, New York, USA
Email: grandyi@outlook.com, futureyiwei@hotmail.com
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 1 February 2015; accepted 3 March 2015; published 10 March 2015
ABSTRACT
The core objective of a chemical composition measurement is to determine its true value. However, when measuring the composition of a macroscopic sample with a large number of atoms or molecules, realizing the true value of the measurand at both the macroscopic and microscopic levels remains an unsolved theoretical problem. We find that the true value of a sample composition exists in any subsample of a homogeneous molecular population of the sample. Here, we propose the Central Law of Measurement of the Amount of Substance: “The homogeneity of a sample molecular population represents the measurement accuracy of the sample composition in an analytical procedure”. The Central Law is based on a homogeneous molecular population axiom in which the molecular composition of a sample is identical for any homogeneous subsample. Furthermore, we point out that, at the microscopic scale, Avogadro’s law does not hold true.
Keywords:
Amount of Substance, Avogadro Constant, Mole, Accuracy, Homogeneity, Central Law

1. Introduction
The determination of a sample composition means the measurement of the amount of chemical elements. The International System of Quantities defines the quantity, the “amount of substance”, to be proportional to the number of specified elementary entities in a sample. The measurement of the amount of substance implies not only the determination of the size (number) of moles at the macroscopic scale but also the determination of the number of elementary entities at the microscope scale. In chemical composition measurement one’s concern focused on the uncertainty of the measured value for the reliability of measurement results [1] [2] . In the paper the objective of measurement focuses on the true value of a sample composition as a function of chemical measurement process.
Measurements of the amount of substance play a critical role in the understanding of a range of topics from particle physics to practical applications, such as biomedical testing, environmental monitoring, and quality control in industrial production. Each day, millions of such measurements are carried out worldwide, forming the bases for many important medical, environmental, economic, and legal decisions which rely on their accuracy [3] [4] . The “true value” is the philosophical basis of accurate measurement [5] . The objective of measurement (the true value of the measurand) in the Error Approach and the Uncertainty Approach is different [2] [6] : “in the Error Approach the objective of measurement is to determine an estimate of the true value that is as close as possible to that single true value, and in practice the true quantity value is considered unknowable. The International Electrotechnical Commission (IEC) does not use the concept to describe this objective. In the Guide to the Expression of Uncertainty in Measurement (GUM), the concept of true value is kept for describing the objective of measurement. The objective of measurement in the Uncertainty Approach is not to determine a true value as closely as possible. Rather, it is assumed that the information from measurement only permits assignment of an interval of reasonable values to the measurand. Additional relevant information may reduce the range of the interval of values that can reasonably be attributed to the measurand”. In the International Vocabulary of Metrology (VIM), the concept of the true value is retained because of common usage and the importance of the concept, and true value of a quantity is consistent with the definition of a quantity [6] .
In general, the true value of the measurand is elusive and unknown [7] -[9] . William John Youden stated that, in a chemical composition measurement, “There is no solution to the problem of devising a single number to represent the accuracy of a procedure” [9] [10] . In practical measurement, the uncertainty and traceability of measurement results tend to be emphasized, whereas the object of realizing the true value of the measurand is evaded. The traceability of results of a chemical measurement has been questioned [11] . Furthermore, the theoretical exploration of the accurate measurement of the amount of substance is neglected. Indeed, for the measurement of the amount of substance, how to realize the true value of a sample composition on a solid theoretical basis remains unsolved. In this paper, the concept of the true value of a sample composition is consistent with the definition of the sample composition at atomic and molecular level. Once a sample is chosen, its atomic and molecular constituents remain unchanged i.e. the numbers of the atoms and molecules remain unchanged, and thus, the sample composition, the ratio of the number of atoms of an analyte element to the total number of atoms of all elements in a sample exists. According to the entry 2.11 of the VIM [6] : “true value of a quantity consistent with the definition of a quantity”, the true value of a sample composition exists. We find that the true value of a sample composition exists in any subsample of the homogeneous molecular population of a sample. We investigate the true value of the sample composition as well as the corresponding sample’s molecular population as a function of a chemical measurement process.
2. Central Law of Measurement of the Amount of Substance
A central question for the measurement of the amount of substance is to search for the true value of a sample composition in the chemical measurement process at both the microscopic and macroscopic scales. In the context of the accurate determination of the Avogadro constant, we have formulated the amount of substance measurement homogeneity principle [12] . A consequence of this principle is that the accuracy of a measurement of the amount of substance is limited by the homogeneity of the sample’s molecular population. In the determination of the silicon molar mass of a single crystal, we found that the degree of heterogeneity of the chemical compositions of the sample is the determining factor to measure silicon molar mass with a relative uncertainty of the order of 10−8. Due to the limit of chemical measurement method and measurement instrument, the assessment limitation of homogeneity is not better than the sensitivity and resolution of a measurement method, and quantitative analytical chemistry to this level of accuracy was not readily available. Theoretically when a sample is chosen, if an analytical procedure does not disturb the sample composition and no measurement error occurs, then the true value can be determined.
By definition, for a homogeneous molecular population in a sample, we know that the molecular composition is identical for any homogeneous subsample. Based on the homogeneous molecular population axiom, if we mix all the molecules in a sample to afford a homogeneous molecular population, then any homogeneous subsample can represent the composition of the whole sample. Therefore, in order to realize the true value of the sample composition, we must maintain the molecular composition of the sample as unchanged and homogeneous in every analytical procedure. The homogeneous molecular population axiom is the theoretical basis of the Central Law. Accordingly, to measure the amount of substance, the measurement process must be performed such that the sample’s molecular population in each operational step is directly related to the true value of the measurand.
Starting from the homogeneous molecular population axiom for a sample―“the molecular composition of the sample is identical for any of its homogeneous subsamples”―we can conceive a homogenization thought experiment, as shown in Figure 1. Here, an original sample is changed into a virtual homogeneous original sample. Therefore, the true value of the original sample composition is equal to the composition of any homogeneous subsample of the virtual homogeneous original sample. Thus, the true value of a sample composition embodying the entire molecular population exists in any homogeneous molecular population of the sample. The true value of a sample composition is there. This is the essence of the Central Law. Figure 1 illustrates the invariant “true value” of the amount-of-substance fraction in the homogeneous molecular population of a sample. The very existence of the true value of a sample composition constitutes the theoretical basis of the Central Law of Measurement of the Amount of Substance as well as the amount-of-substance measurement homogeneity principle.
It is well known that matter consists of atoms and molecules. The measurement of the sample composition strives to determine the atomic and molecular constituents of a sample, i.e. to measure the atomic and molecular population(s). Therefore, the results of measuring the sample composition reflect the molecular population of the sample constituents. From the relationship between a sample molecular population and the measurement result of the sample composition, we can prove that the homogeneity of a sample’s molecular population represents the measurement accuracy of the sample composition in an analytical procedure. This is an important point for understanding accurate measurement of the amount of chemical elements on both the microscopic and macroscopic scales.
For clarity, some of the vocabulary and terminology used in this paper is explained here. According to the International Vocabulary of Metrology, “accuracy” is defined as the “closeness of agreement between a measured quantity value and a true quantity value of a measurand” [6] . Similarly, the “homogeneity of the sample molecular population” is defined as “the closeness of agreement between a sample molecular population and the homogeneous molecular population of a sample”. We discuss the homogeneity of a sample itself for all the atoms and molecules of the sample, regardless of the measurement method. The more homogeneous the sample, the smaller will be the sample size required to represent the true value of the total molecular population of the sample. From the viewpoint of the measurement result of the amount of substance relative to a molecular population of a sample, a measured quantity value should correspond to the molecular population of any sample taken from that population. Under the condition of a homogeneous molecular population, any subsample of the homogeneous molecular population of a sample will be representative of the true value of the sample composition, as shown in Figure 2. Therefore, the homogeneity of a sample molecular population represents the measurement accuracy of the sample composition.
Figure 2 shows the relationship between the sample molecular population (microscopic scale) and measurement results (macroscopic scale) for the determination of a sample composition. It demonstrates that the true value of a sample composition is related to the homogeneous molecular population of the sample, and a measured value of a sample composition is related to a molecular population of the sample of the measured value acquired. Thus, the homogeneity (the closeness of agreement between a sample molecular population and the homogeneous molecular population of a sample) of the sample molecular population corresponds to the measurement accuracy (the closeness of agreement between a measured quantity value and the true quantity value of
Figure 1. Maintaining the true value of a sample composition in the homogeneous molecular population.
Figure 2. Schematic showing the relationship between the sample molecular population (microscopic scale) and measurement results (macroscopic scale).
the measurand) of the sample composition.
3. Mathematical Proof Combined with a Homogenization Thought Experiment
In order to prove the Central Law mathematically, the amount-of-substance fraction of a sample composition should be expressed and measured in terms of the number of microscopic elementary entities. Suppose a sample S contains all the possible, though not necessarily all, stable elemental substances in the periodic table of the elements [13] , and each element has k isotopes. Once the sample S is chosen, its elemental composition remains unchanged and no element decay processes occur. For a sample S composed of the isotopic element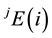 , all
, all
the isotopic elements are identical, and the atom number of this element 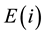 is given by
is given by , where
, where 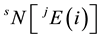 is the number of atoms of the element
is the number of atoms of the element 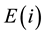 with the jth isotope in sample S. Then, the total atom number of all elements is
with the jth isotope in sample S. Then, the total atom number of all elements is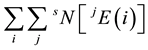 . By the definition of the amount-of-substance fraction, the amount-of-substance fraction
. By the definition of the amount-of-substance fraction, the amount-of-substance fraction 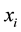 for the element
for the element  is given by
is given by 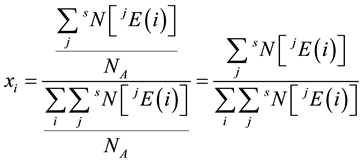 [14] ,
[14] ,
where 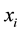 is the amount-of-substance fraction with respect to element
is the amount-of-substance fraction with respect to element 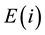 in sample S, and NA is the Avogadro constant.
in sample S, and NA is the Avogadro constant.
According to the entry 2.11 of the VIM [6] , the true value of the amount-of-substance fraction  for the element
for the element 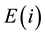 is consistent of the definition of the amount-of-substance fraction
is consistent of the definition of the amount-of-substance fraction  with respect to element
with respect to element


Hence,
As shown in equation (1), the true value of the amount-of-substance fraction of an analyte element is the ratio of the number of atoms of the analyte element to the total number of atoms of all elements.
When a chemical measurement procedure consists of a homogenization process of sample S, the molecular population of sample S will become homogeneous at the molecular level. For any subsample H of the homogeneous molecular population, the number of atoms of the element 




where the subscript hmp stands for any homogeneous molecular population of the sample.
Due to the homogeneous molecular population axiom, in which the molecular composition of a sample is identical for any homogeneous subsample, we have

Hence,

Consequently, in a sample, the true value of the amount-of-substance fraction of an element exists in the entire molecular population of the sample as well as in any homogeneous molecular population of the sample. The true value of a sample composition is invariant for the homogeneous molecular population, as shown in equation (3). Then, the amount-of-substance fraction of the subsample H is equal to the amount-of-substance fraction of the original sample S, i.e. the true value of the sample composition.
Conversely, consider the chemical measurement process consisting of n steps: in the first step the amount-of-
substance fraction for the element 





If we assume that

i.e. the true value of the amount-of-substance fraction 




When a chemical measurement procedure leads to a change in the true value of the sample composition, it simultaneously changes the corresponding sample molecular population. In such an operation, if a measured value 

of a measured sample M, where the atom number of the measured element 



Combining equation (3) with equation (5), we arrive at

Equation (6) is a mathematical expression of the Central Law of Measurement of the Amount of Substance. The left hand side of the Equation (6) represents the measurement accuracy of the sample composition, and the right hand side of the Equation (6) represents the homogeneity of a sample molecular population. Therefore, the homogeneity of a sample molecular population represents the measurement accuracy of the sample composition. We thus answer Youden’s scientific question!
4. Discussion
The Central Law of Measurement of the Amount of Substance tells us whether or not a sample is a homogeneous molecular population after the sample is chosen. To obtain the true value of a sample composition, we must measure all the molecules of the sample, or homogenize the sample at the molecular level and maintain this homogeneity in every measurement procedure. In this way, we can measure a sample composition with the highest accuracy at both the microscopic and macroscopic scales. Accordingly, an accurate chemical measurement process should also be a sample homogenization procedure. Successful homogenization depends on the related molecular properties and the pattern of the chemical conversion as well as the experimental capability and method.
By Equation (3) we know that for a chemical measurement process any change to the numerator or the denominator or the ratio between the numerator and the denominator will have an effect on the true value of a sample’s composition. Here, we notice that all influence factors and sources of uncertainty in a chemical composition measurement will lead the changes of the true value of a sample’s composition. That is why all the sources of uncertainty should be taken into account in the evaluation of overall uncertainty of the measurement results. Therefore, it is essential for obtaining reliable analytical results that the general demand on sampling or chemical preparation or instrument measurement is to maintain the true value of a sample composition, and Equation (3) is a theoretical basis of principle of sampling [15] .
For a multistep analytical procedure, the degree of inhomogeneity of every step of the measurement process will become a sampling error in the next measurement step, and the result reflects the propagation of error over many analytical procedures. Furthermore, in chemical analysis the composition of a sample will be changed by the additional analyte from a preparative reaction process or by the analyte losses in a purifying extraction process. Therefore, the measured value of a sample composition will deviate from the true value of the sample composition. Thus, if we do not ensure a representative sampling, or if we do not obtain a homogeneous sample, then to obtain the true value of a sample composition we must measure the entire sample, i.e. all the molecules of the sample. However, the entire molecular population is rarely measured because of the cost or technical limitations. Accordingly, it is crucial to maintain the homogeneity of a sample’s molecular population. Additionally, the chemical measurement process may itself change the sample’s molecular population and thereby alter the true value of the composition of the original sample.
4.1. Impact of the Chemical Measurement Process on the Molecular Population of the Sample
The impact of a chemical measurement process on the molecular population of the sample and the sample composition is examined as follows. The molecular population of a sample can be influenced in two ways for a chemical measurement process. The first artificially introduces additional analyte and matrix molecules, changing the original composition. Alternatively, some analyte and matrix components may be lost, which may also change the sample’s molecular population. In general, a chemical measurement procedure may include preparative reaction and purifying extraction processes, as well as detection and calibration steps, that can alter the composition of the original sample. For example, in a preparative reaction process, it is not only possible to change the sample’s molecular distribution, but the process may also be a source of additional analyte from the reagents or the environment. Consequently, these factors can change the population of the analyte molecules. However, the changes that result from contamination can be corrected for by accurately measuring the composition of the contaminant. Likewise, the changes from the recovery of the analyte can also be corrected for by accurately measuring the amount-of-substance fraction of the analyte loss in a purifying extraction process.
Let us assume that the number of atoms of the element 



In the purifying extraction process, some loss of analyte may occur and alter the population of the analyte molecules. If the number of lost atoms of the element 




The detection step involves a kinetic detection process and detector response determination. During the kinetic process, the population of the analyte molecules may further change: contaminants from other reagents and the environment may be present and there may be some loss of the analyte. To calibrate the detection results, we need a calibration sample that is homogeneous at the molecular level, and the detection process and conditions for the calibration sample should be the same as those used during sample assessment [12] [16] . The best measured value will be achieved if we can maintain the homogeneity of the sample’s molecular population in every measurement step; accurately measure the analyte in the sample taken; correct the results for contaminant interference from the reagents and environment as well as the loss of the analyte in the analytical procedure (Equation (7)); and calibrate the instrument using homogeneous molecular population samples.
Figure 3 schematically illustrates the measurement characteristics of a sample composition at both the microscopic and macroscopic levels.
The Central Law of Measurement of the Amount of Substance provides the theoretical basis for seeking the true value of a sample composition in the development of new measurement methods and techniques.
4.2. Manipulating the Entities and Counting the Number of Entities
The accurate measurement of the amount of substance ultimately involves the accurate measurement of the number of entities. A mole is defined as “the amount of substance of a system which contains as many elementary entities as there are atoms in 0.012 kilogram of the isotope carbon 12” [17] [18] . The number of elementary entities in one mole is known as the Avogadro number and has the value 6.02214129(27) × 1023 [19] . Unbound atoms of carbon 12, at rest and in their ground state, are understood. The Avogadro constant NA relates any quantity on the atomic scale to its corresponding macroscopic scale: a macroscopic quantity is NA times its corresponding microscopic quantity [20] .
To count the entities accurately, first one must correctly identify the entities to be counted. Even for larger en-
Figure 3. Schematic representation of the measurement of a sample composition.
tities such as cells, it was reported that 20% of the published work using human cell lines was misidentified due to cell line cross-contamination [21] [22] . To identify an elementary entity, one must know its microscopic quantum state and physical properties. Since detectors may incorrectly identify different types of atoms in similar quantum states as being the same types of atoms, or discern the same types of atoms in different quantum states as being different types of atoms, distinguishing between the different quantum states of the same atoms would enhance the counting uncertainty. Therefore, the same microscopic parameters of the measured atoms are a prerequisite for identifying and counting the exact number of atoms. That is, in order to realize the exact determination of the Avogadro constant through identical entities, all the identical entities should be in the same quantum state. Counting such a huge number of atoms individually within an acceptable timeframe is clearly impossible [23] [24] . The homogeneity of the microscopic entity population is an indispensible condition for the accurate determination of the amount of substance at both the macroscopic and microscopic scales.
In chemical analysis it is more difficult to correctly detect the sample molecular population for a complex sample. Matrices, for example, may affect the analyte molecular distribution of the sample during the kinetic process of detection, and may also interfere with the detector response [25] [26] . Consequently, the process of detection may further alter the true value of a sample composition. If one obtains the sample molecular constituents in an uncontrolled atomic or molecular detection process, the measurement result of the sample composition will have some uncertainty. Therefore, the compositional measurement of a complex sample should seek a balance between maintaining the homogeneity of the molecular population and minimizing interference with the detector response. Moreover, the instrument sensitivity and resolution do not always meet the individual requirements for measuring different entities. At that moment, the measurement results of the amount of substance have a certain uncertainty. The true value of a sample’s composition can only be realized without uncertainty if the detection result is achieved by correctly identifying the atoms one by one. Otherwise, this value would only be a statistical result. Counting the number of atoms or molecules is difficult, and the manipulation and control of these atoms or molecules before counting is even more difficult. There can be no exact counting of the number of atoms without atomic manipulation. In fact, chemical measurements directly reflect our capability to manipulate the sample molecules.
The most widely used method for the measurement of the mole is to weigh pure material according to the equation

where n is the amount of substance, m is the mass of the pure material, and 
4.3. Some Remarks on the Mole
Early in 1811, the Italian chemist Amedeo Avogadro stated that “equal volumes of gases at the same temperature and pressure contain the same number of molecules regardless of their chemical nature and physical properties”. This principle is known as Avogadro’s law or Avogadro’s hypothesis. Avogadro’s great contribution was to introduce the concept of molecules two hundred years ago. Approximately one hundred years later, the French physicist Jean Baptiste Perrin experimentally verified the existence of molecules. The concept of the mole originates in the “gram-molecule”, which refers to an amount of a compound equal to its molecular weight expressed in grams. Perrin explained the term “gram-molecule” as follows [28] [29] : “any two gram-molecules contain the same number of molecules. This invariable number N is a universal constant, which may appropriately be designated Avogadro’s Constant”. Here, we suggest that, at the microscopic scale, Avogadro’s law is a false proposition. Let us falsify the hypothesis.
In fact, temperature and pressure are macroscopic descriptions of properties in thermal equilibrium. These thermodynamic state quantities are defined (and measurable) only at equilibrium [30] . The physical quantities which describe a macroscopic body in equilibrium are, almost always, very nearly equal to their mean values, but deviations and/or fluctuations do occur. Even though they are generally small, the very presence of fluctuations is of great physical significance [31] [32] . For an ideal gas system at thermodynamic equilibrium, the relative fluctuation of the number of particles is just the reciprocal square root of the mean number of particles [32] [33] :

where Na is the number of particles of the system, 
If Na = 1023, then the relative root-square fluctuation in the number of particles of the given system is on the order of 10−12 and, hence, negligible (small at macroscopic level). But the fluctuation in the number of particles of the given system is of the order of 1011 (big at microscopic level). This is to say for an ideal gas thermodynamic equilibrium system of a certain macroscopic temperature, pressure and volume with particle numbers 1023, because the fluctuation in the number of particles is of the order of 1011, the number of particles is not unique, it has a set of values. However, Avogadro’s law stated that equal volumes of gases at the same temperature and pressure contain the same number of molecules (i.e. the number of particles is unique). That’s not true. In a gas thermodynamic equilibrium system the macroscopic quantities such as temperature, pressure and volume cannot define the unique number of microscopic molecules. Actually, the number of particles has a set of values with equal volumes of gases at the same temperature and pressure. Due to fluctuations, the measurement of a change smaller than the fluctuations is impractical. Theoretically, based on a thermal equilibrium system, the uncertainties of the measurement results for the thermodynamic quantities are not better than their fluctuations.
Since Avogadro’s law is an experimental law, when
the microscopic molecules are in fact indistinguishable, according to the macroscopically measured values such as pressure, temperature, and volume, which exhibit uncertainties that are much higher than 1 × 10−12. The measured number of molecules is meaningful only within the uncertainties of the measurement results of these macroscopic thermodynamic state quantities. It is impossible to define a unique number of molecules in a thermodynamic equilibrium system, in the case in which there are the thermodynamic fluctuations of the number of molecules. In summary, at the microscopic scale, Avogadro’s law does not hold.
Therefore, the Avogadro constant based on this law is not actually a physical constant, and the theoretical uncertainty of the number of molecules is no less than its fluctuation. Based on the 1971 definition of the mole and the 1980 supplement [17] , the Avogadro constant became a real physical constant. The relationship between a macroscopic sample mass and a certain number of molecules is the essential characteristic of the mole concept, and the inherent basis of this relationship is the homogeneous molecular population of the macroscopic sample. Avogadro’s constant is the very bridge between the macroscopic quantity and the microscopic quantity. By the 1971 definition of the mole, we have

where n is the amount of substance, N is the number of specified elementary entities, and NA is the Avogadro constant.
To ensure the accurate measurement of the amount of chemical elements, the definition and the method for realizing the true value of a sample composition should be consistent. The key issue is to measure the number of molecules of a sample composition at the microscopic scale. Unfortunately, in the measurement of the amount of substance, the results of a sample composition are usually achieved through a macroscopic measured quantity without ensuring the homogeneity of the sample molecular population. Moreover, the uncertainty of the macroscopic measured quantity is far from the requirement for an exact determination of the number of molecules.
5. Conclusion
Recognizing that matter is composed of atoms and molecules, a measurement result as displayed on a chemical detector reflects the molecular population reaching the detector at a given time. For an accurate measurement of the amount of substance at both the macroscopic and microscopic levels, the homogeneity of the sample at the molecular level is essential. The true value of a sample composition is preserved in any homogeneous molecular population of the sample as well as in the total molecular population of the sample. By its very nature, measurement should always aim for the true value of the measurand. To realize this objective, one must maintain the true value unchanged in every analytical procedure. In essence, the measurement of the amount of substance is not a simple problem of atomic or molecular counting, but whether or not one can sufficiently manipulate and control the large number of atoms and molecules to be measured. The true value of a sample composition can only be realized if we have the capability to correctly identify atoms individually. Without this capability, we can only obtain a best value of a sample composition with some statistical uncertainty. The homogeneous molecular population of a macroscopic sample inherently underlies the exact relationship between a certain number of molecules and a physical quantity of the molecular constituents, regardless of the number of molecules of a homogeneous subsample. Assuring the homogeneity of a sample’s molecular population is the microscopic mechanism by which to maintain the measurement accuracy of the sample composition. Manipulating and controlling the molecules of a sample are prerequisites to guarantee the realization of the true value of the sample composition. The Central Law of Measurement of the Amount of Substance is a fundamental law for the accurate measurement of the amount of substance at the macroscopic and microscopic levels.
Acknowledgements
The authors would like to thank Dr. Robert Wielgosz for inviting Hong Yi to present this work at CCQM/BIPM workshop on “The redefinition of the mole: A new era of chemical metrology” in April 2012. We are grateful to Prof. Dr. Paul De Bievre for his valuable comments on an earlier draft of this paper. All errors remain the authors’ responsibility.
References
- De Bièvre, P. and Günzler, H. (2003) Measurement Uncertainty in Chemical Analysis. Springer-Verlag, Berlin. http://dx.doi.org/10.1007/978-3-662-05173-3
- BIPM, IEC, IFCC, ILAC, ISO, IUPAC, IUPAP and OIML (2008) Guide to the Expression of Uncertainty in Measurement (GUM). JCGM 100:2008. http://www.bipm.org/utils/common/documents/jcgm/JCGM_100_2008_E.pdf
- De Bievre, P., Kaarls, R., Peiser, H.S., Rasberry, S.D. and Reed, W.P. (1996) Measurement Principles for Traceability in Chemical Analysis. Accreditation and Quality Assurance, 1, 3-13. http://dx.doi.org/10.1007/s007690050026
- Cali, J.P. (1974) A Systematic Approach to Accuracy in Clinical Chemistry. Medical instrumentation, 8, 17-21.
- Dorsey, N.E. and Eisenhart, C. (1953) On Absolute Measurement. The Scientific Monthly, 77, 103-109.
- BIPM, IEC, IFCC, ILAC, ISO, IUPAC, IUPAP and OIML (2012) International Vocabulary of Metrology-Basic and General Concepts and Associated Terms (VIM). 3rd Edition, JCGM 200:2012. http://www.bipm.org/utils/common/documents/jcgm/JCGM_200_2012.pdf
- Cali, J.P. and Reed, W.P. (1976) The Role of the National Bureau of Standards Standard Reference Materials in Accurate Trace Analysis. National Bureau of Standards Special Publication, 422, 41-63.
- De Bievre, P. and Taylor, P.D.P. (1997) Traceability to the SI of Amount of Substance Measurements: From Ignoring to Realizing, a Chemist’s View. Metrologia, 34, 67-75.
- Youden, W.J. (1961) How to Evaluate Accuracy. Materials Research & Standards, 1, 268-271.
- Kadis, R. (2002) Analytical Procedure in Terms of Measurement (Quality) Assurance. Accreditation and Quality Assurance, 7, 294-298. http://dx.doi.org/10.1007/s00769-002-0484-9
- Price, G. (2011) Failures of the Global Measurement System Part 1: The Case of Chemistry. Accreditation and Quality Assurance, 15, 421-427. http://dx.doi.org/10.1007/s00769-010-0655-z
- Yi, H., Li, T.J., Wang, X., Zhang, F.S., Huo, W.G. and Yi, W. (2012) Amount of Substance Measurement Homogeneity Principle: The Discrepancy between XRCD and Watt Balance Results. Metrologia, 49, 62-69. http://dx.doi.org/10.1088/0026-1394/49/1/010
- http://www.iupac.org/fileadmin/user_upload/news/IUPAC_Periodic_Table-1Jun12.pdf
- Mills, I., Cvitaš, T., Homann, K., Kallay, N. and Kuchitsu, K. (1993) IUPAC Green Book: IUPAC Quantities, Units and Symbols in Physical Chemistry. 2nd Edition, Blackwell Scientific Publications, Oxford.
- Danzer, K. (2007) Analytical Chemistry Theoretical and Metrological Fundamentals. Springer, Berlin, 15.
- Cuadros-Rodriguez, L., Gamiz-Gracia, L., Almansa-Lopez, E. and Laso-Saènchez, J. (2001) Calibration in Chemical Measurement Processes: I. A Metrological Approach. Trends in Analytical Chemistry, 20, 195-206. http://dx.doi.org/10.1016/S0165-9936(00)00093-5
- BIPM (2006) The International System of Units (SI). 8th Edition, BIPM, Paris. http://www.bipm.org/utils/common/pdf/si_brochure_8.pdf
- Milton, M.J.T. (2011) A New Definition for the Mole Based on the Avogadro Constant: A Journey from Physics to Chemistry. Philosophical Transactions of the Royal Society A, 369, 3993-4003. http://dx.doi.org/10.1098/rsta.2011.0176
- http://physics.nist.gov/cgi-bin/cuu/Value?na|searchfor=avogadro+constant
- Becker, P. (2001) History and Progress in the Accurate Determination of the Avogadro Constant. Reports on Progress in Physics, 64, 1945-2008. http://dx.doi.org/10.1088/0034-4885/64/12/206
- MacLeod, R.A.F., Dirks, W.G., Matsuo, Y., Kaufmann, M., Milch, H. and Drexler, H.G. (1999) Widespread Intraspecies Cross-Contamination of Human Tumor Cell Lines Arising at Source. International Journal of Cancer, 83, 555- 563. http://dx.doi.org/10.1002/(SICI)1097-0215(19991112)83:4<555::AID-IJC19>3.0.CO;2-2
- Drexler, H.G., Dirks, W.G., Matsuo, Y. and MacLeod, R.A. (2003) False Leukemia-Lymphoma Cell Lines: An Update on Over 500 Cell Lines. Leukemia, 17, 416-426. http://dx.doi.org/10.1038/sj.leu.2402799
- Wheatley, N. (2011) On the Dimensionality of the Avogadro Constant and the Definition of the Mole. Metrologia, 48, 71-82. http://dx.doi.org/10.1088/0026-1394/48/3/001
- Milton, M.J.T. and Quinn, T.J. (2001) Primary Methods for the Measurement of Amount of Substance. Metrologia, 38, 289-296. http://dx.doi.org/10.1088/0026-1394/38/4/1
- Prichard, E. and Barwick, V. (2007) Quality Assurance in Analytical Chemistry. John Wiley & Sons Ltd., England, 70-73. http://dx.doi.org/10.1002/9780470517772
- Matuszewski, B.K., Constanzer, M.L. and Chavez-Eng, C.M. (2003) Strategies for the Assessment of Matrix Effect in Quantitative Bioanalytical Methods Based on HPLC-MS/MS. Analytical Chemistry, 75, 3019-3030. http://dx.doi.org/10.1021/ac020361s
- Andreas, B., Azuma, Y., Bartl, G., Becker, P., Bettin, H., Borys, M., et al. (2011) Counting the Atoms in a 28Si Crystal for a New Kilogram Definition. Metrologia, 48, S1-S13. http://dx.doi.org/10.1088/0026-1394/48/2/S01
- Milton, M.J.T. (2013) The Mole, Amount of Substance and Primary Methods. Metrologia, 50, 158-163. http://dx.doi.org/10.1088/0026-1394/50/2/158
- Perrin, J.B. (1910) Brownian Movement and Molecular Reality. Taylor and Francis, London.
- Greiner, W., Neise, L. and Stocker, H. (1995) Thermodynamics and Statistical Mechanics. Springer, New York, 6. http://dx.doi.org/10.1007/978-1-4612-0827-3
- Pathria, R.K. and Beale, P.D. (2011) Statistical Mechanics. 3rd Edition, Elsevier, Singapore, 583-586. http://dx.doi.org/10.1016/B978-0-12-382188-1.00015-3
- Landau, L.D. and Lifshitz, E.M. (1986) Statistical Physics Part 1. 3rd Edition, Elsevier, Singapore, 333-345.
- Schwabl, F. (2006) Statistical Mechanics. 2nd Edition, Springer, Berlin, 494-496.




