American Journal of Analytical Chemistry
Vol.4 No.8(2013), Article ID:35444,8 pages DOI:10.4236/ajac.2013.48048
Adsorption of Natural Aluminium Dye Complex from Silk-Dyeing Effluent Using Eucalyptus Wood Activated Carbon
School of Chemical Engineering, Institute of Engineering, Suranaree University of Technology, Nakhon Ratchasima, Thailand
Email: *chaiyot@sut.ac.th
Copyright © 2013 Saowanee Chuyingsakuntip, Chaiyot Tangsathitkulchai. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received May 17, 2013; revised June 20, 2013; accepted July 15, 2013
Keywords: Adsorption; Activated Carbon; Dyeing Effluent; Eucalyptus Wood
ABSTRACT
Two activated carbons with controlled pore size were prepared from Eucalyptus wood by physical activation with carbon dioxide, giving the BET surface area and pore volume of 738 m2/g and 0.39 cm3/g, and 921 m2/g and 0.53 cm3/g for the carbon sample AC1 and AC2, respectively. These activated carbons were then used to remove the residual dye left after the silk-dyeing process. The dye solution used for adsorption study was a cationic aluminium dye complex of [Al(brazilein)2]+ derived from a mixture of alum and extract of the heartwood of Ceasalpinia sappan Linn., with initial dye concentration of 220 mg/l. Effects of adsorbent dosage, adsorption time and temperature in the range of 25˚C - 40˚C on dye adsorption were investigated. It was found that the adsorption kinetics of this dye complex was best described by the pseudo-second order model. Adsorption isotherms of this dye complex were well fitted by Langmuir isotherm equation. The adsorption capacities for the uptake of this dye complex at 25˚C, 30˚C and 40˚C were 718.7, 1240.4 and 1139.5 mg/g and 1010.5, 1586.1 and 1659.0 mg/g for carbon sample AC1 and AC2, respectively. From these results, it can be concluded that activated carbon containing a higher proportion of mesopores gave better dye removal efficiency, emphasizing the fact that a proper pore size distribution of carbon adsorbent is crucial for the effecttive removal of relatively large size of the dye molecules. Thermodynamic parameters, including free energy, enthalpy and entropy of adsorption, were also determined. The adsorption enthalpies for the removal of this dye complex of AC1 and AC2 were 105.3 and 55.6 kJ/mol, respectively, indicating that the adsorption is an endothermic process. It was found that the adsorption of this dye complex is spontaneous at the temperatures under investigation.
1. Introduction
The aqueous extract from the heartwood of Ceasalpinia. Sappan Linn. is traditionally used for the dyeing of silk by villagers in the northeast of Thailand. The extracted dye, which consists mainly of brazilein (see Figure 1(a)), imparts a beautiful red or pink color to the silk [1]. An alum mordant is generally added to the dye solution to form a cationic dye complex of [Al(brazilein)2]+ (see Figure 1(b)) which helps improve the fastness property of dye onto silk. The effluent left from the silk dyeing exhibits high color and the discharge can cause a serious problem and concern to the environment. There are various methods available for treating dyeing effluents such as membrane separation [2], eletrochemical method [3], coagulation/flocculation [4], and biological processes [5-7] etc., with each method having its own limitation in terms of cost and effectiveness. Of these treatment processes, adsorption is an attractive separation process for removing a number of pollutant species from wastewater, due to its process simplicity, low energy operation and capability of adsorbent regeneration [8,9]. Among commercial adsorbents, activated carbon is most widely used for liquid-phase adsorption because of its many advantages such as low cost, large internal area (typically 1000 m2/g) and the required pore size distribution can be easily achieved by controlling the preparation conditions [10-12].
 (a)
(a) (b)
(b)
Figure 1. Chemical structure of (a) Brazilein and (b) [Al(brazilein)2]+ complex.
In this study, activated carbons prepared from eucalyptus wood by physical activation with carbon dioxide were used to remove residual cationic dye of [Al(brazilein)2]+ from real silk-dyeing effluent. The effect of carbon porous structure on the kinetics, equilibrium, and thermodynamics of dye adsorption was investigated.
2. Materials and Methods
2.1. Activated Carbon Preparation and Characterization
Eucalyptus wood (Eucalyptus camaldulensis Dehn.) in the form of shaving was milled and sieved to obtain a size fraction of 20 × 30 mesh (0.714 mm average size). The wood sample was then dried in an oven at 110˚C for 24 h to remove excess moisture. Next, about 7 g of the dried sample was placed in a ceramic boat and carbonized in a tube furnace (Carbolite, UK) at 400˚C under the flow of N2 (100 cm3/min) for 60 min. The derived char was further activated with carbon dioxide at a rate of 100 cm3/min in a stainless steel packed-bed reactor (2.5 cm I.D. and 10 cm long) inserted in a tube furnace. Two activation conditions, 800˚C for 60 min and 900˚C for 90 min, were employed to produce activated carbon with different porous structure and the resulting carbons were designated as AC1 and AC2, respectively.
The eucalyptus wood was characterized for proximate analysis and lignocellulosic compositions using the procedures outlined by Tangsathitkulchai et al. [13]. Specific surface area and pore volume of activated carbon were determined from nitrogen adsorption isotherms obtained at −196˚C provided by an automated adsorption apparatus (Micromeritics ASAP2010). Adsorption theories and models required for calculating porous properties of activated carbon from isotherm data are well documented by Rouquerol et al. [14].
2.2. Preparation of Dye-Complex Solution
The heartwood of Ceasalpinia sappan Linn. was collected from plantation areas in Nakhon Ratchasima province, Thailand. The wood was reduced into small sizes (~0.3 cm × 3 cm) and boiled in deionized water, using the ratio of 1 g wood per 100 ml water, for 2 h at 80˚C - 90˚C. The aqueous extract was filtered and dewatered by a rotary evaporator (R-210, Buchi), followed by drying in a vacuum freeze dryer (DW3 Drywinner, Hito) to give the extract in powder form.
Next, the alum-dye complex solution for silk dyeing was prepared by mixing the stock solution of dye powder (5 × 10−4 M, 100 mL) with alum [KAl(SO4) 12.H2O] (5 × 10−4 M, 200 mL), giving alum-to-dye mole ratio of 2:1. The dye complex formed is present in the dye bath as a cationic complex, [Al(brazilein)2]+ or [Al(C16H14O5)2]+, which has a molar mass of 599 g/mol [1]. The existence of this aluminium dye complex in the dye solution was ascertained by the application of electrospray ionization mass spectrometry (ESI-MS); the details of measurement and results can be found elsewhere [15]. The dyeing was performed by mixing 5 g of silk yarn with 50 mL of the prepared dye-complex solution and shaken in a water-bath shaker at room temperature for 2 h. The dye solution left after the dyeing process was further diluted with water to obtain the dye solution with initial concentration of 220 mg of dye/L solution and was used for the subsequent adsorption experiments.
2.3. Adsorption Experiments
Tests were carried out to obtain adsorption isotherms of the dye complex by AC1 and AC2 as follows. For each run, 25 mL of dye solution (220 mg/L) was mixed with a fixed amount of activated carbon and shaken at a set temperature (25˚C, 30˚C and 40˚C) in a thermostat shaking bath until the equilibrium was reached (~72 h). The amount of carbon used was varied from 0.005 - 0.025 g. The equilibrium concentration of dye in the solution was determined from a calibration curve constructed based on the measured absorbance of standard dye solutions, using a UV-visible spectrophotometer (model 8453, Agilent) run at the wavelength (λmax) of 509 nm. The amount of dye adsorbed can be calculated from the following equation.
 (1)
(1)
where qe is the amount of dye adsorbed at equilibrium (mg/g carbon), Co and Ce are the dye concentration (mg/L) at time t = 0 and at equilibrium, respectively, V is the solution volume (L) and W is the amount of carbon used (g). Experiments were also performed to study the effect of time (adsorption kinetics), carbon dosage, and temperature on the adsorption of this Al-dye complex from aqueous solution. Since the primary purpose of this work was to study the effect of pore texture of activated carbon on dye adsorption but not the effect of surface chemistry, no attempt was made at this stage to investigate the influence of solution pH on the dye removal. Therefore, dye solution with the initial natural pH of 4.0 was used throughout the adsorption experiments.
3. Results and Discussion
3.1. Material Characterization
Table 1 shows the proximate analysis and lignocellulosic composition of eucalyptus wood studied in this work. The results indicate that eucalyptus wood contains a high proportion of volatile matters but with relatively low ash content. The fixed carbon content is comparable to other biomass materials used for the production of activated carbon, for example, corn cob (16.1%) [16], coconut shell (18.6%) [17], and pistachio nut shell (21.6%) [18]. Eucalyptus wood studied in the present work is classified as hard wood type, based on the following range of lignocellulosic contents for hard wood: cellulose (57% - 62%), hemicellulose (12% - 16%) and lignin (25%) [19].
The porous properties of prepared activated carbons are listed in Table 2. It is observed that sample AC2 has

Table 1. Chemical analysis of eucalyptus wood.

Table 2. The porous properties of activated carbon.
larger average pore size, higher surface area and pore volume and contains greater mesopore volume than those of sample AC1. Figure 2 shows the nitrogen adsorption isotherms of the two carbons used for the pore characterization. As seen, the isotherm of sample AC1 shows Type I isotherm, typical of microporous adsorbent, while AC2 displays Type II isotherm with small hysteresis loop which is indicative of a mesoporous adsorbent. It has been reported that the pore structure of activated carbon plays a significant role in determining its adsorbed capacity and the transport of adsorbate molecules within the pores can be strongly limited by the steric effect due to the molecular size and shape of adsorbate relative to the pore size [20].
Figure 3 shows SEM images of carbon samples AC1 and AC2. Visually, sample AC2 possesses larger pore size as compared with AC1, in accord with the pore texture results reported in Table 2.
3.2. Effect of Adsorbent Dosage
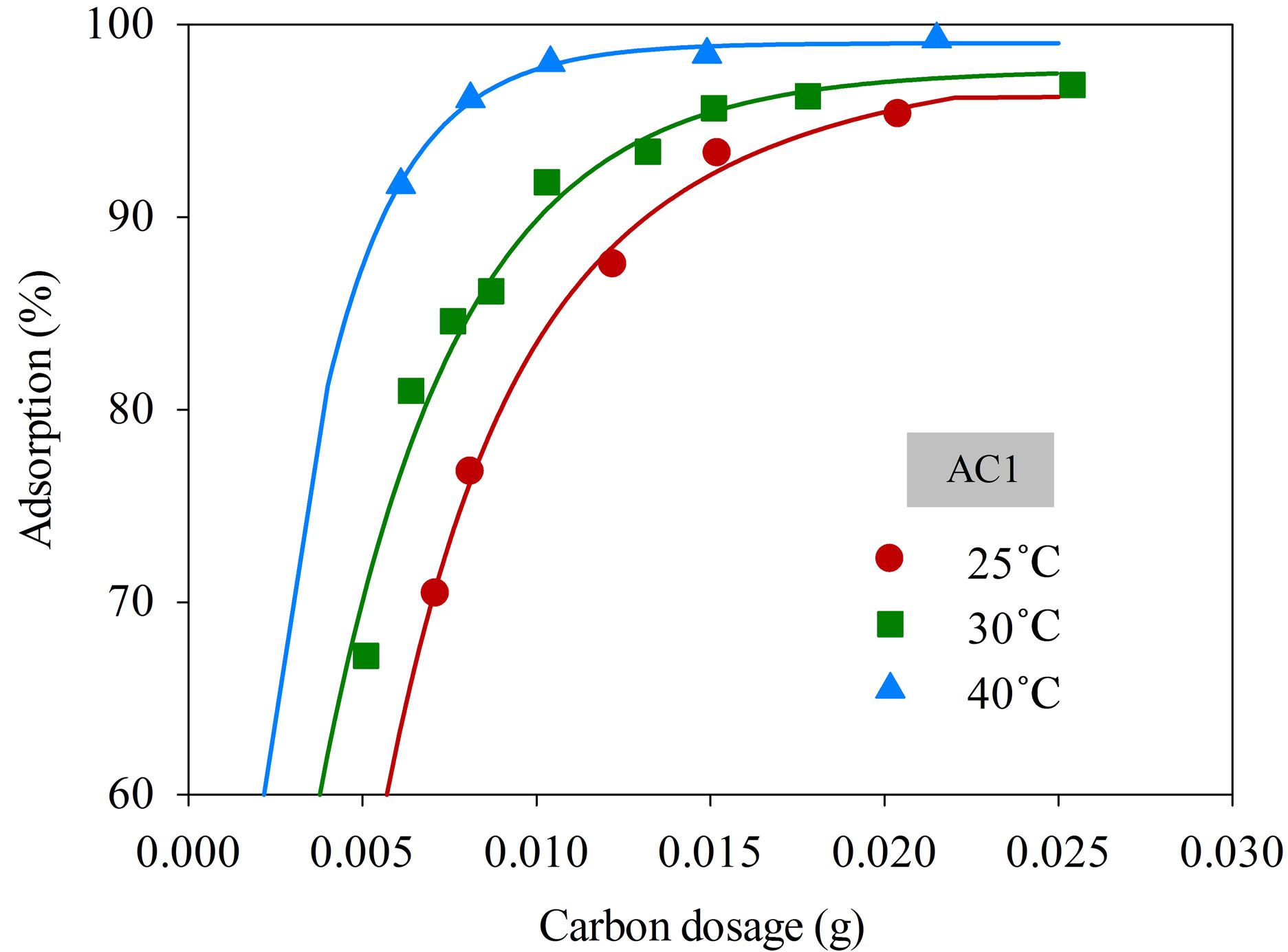
Figure 4 shows the effect of adsorbent dosage on the percentage removal of dye complex with samples AC1 and AC2 at different adsorption temperatures from 25˚C to 40˚C, using initial dye concentration and solution volume of 220 mg/L and 25 mL, respectively. It is seen that the amount of dye adsorbed was increased with increasing adsorbent dosage from 0.005 to 0.025 g. More than 95% adsorption efficiency could be achieved using the carbon amount of 0.025 g for both the AC1 and AC2 at all adsorption temperatures. The results indicate that the uptake of this cationic dye by these two activated carbons depends directly on the amount of adsorbent used. Obviously, the increased adsorption should arise from the increased number of active sites for adsorption with increasing amount of adsorbent used. Consequently,

Figure 2. Adsorption (closed symbols) and desorption (open symbols) isotherms of N2 at 77 K of tested activated carbons.
 (a)
(a) (b)
(b)
Figure 3. SEM photographs of AC1 and AC2 activated carbons.
a fixed amount of activated carbon of 0.025 g was employed for the kinetic study of dye adsorption in this work.
3.3. Adsorption Kinetics
The effect of time on the adsorption of dye complex is shown in Figure 5" target="_self"> Figure 5. The amount of dye adsorbed increased rapidly for the first 500 min, followed by a slow increase and finally attained the equilibrium at around 4000 min. The relatively long equilibrium time reflects the slow diffusion of large molecular size of the dye complex and possibly by the hindering among the dye molecules. It is also noted that the adsorption is favored by the increasing of temperature. This could be attributed to the increased mobility of the dye molecules inside the pores and the lowering in the liquid viscosity as the temperature is increased [21].
The adsorption kinetics of natural dye complex by eucalyptus based activated carbons was analyzed using the pseudo first-order model [22], the pseudo secondorder model [23] and the pore diffusion or intra-particle diffusion model [24]. These kinetic equations are given as follows:
Pseudo first-order kinetic model:
 (2)
(2)
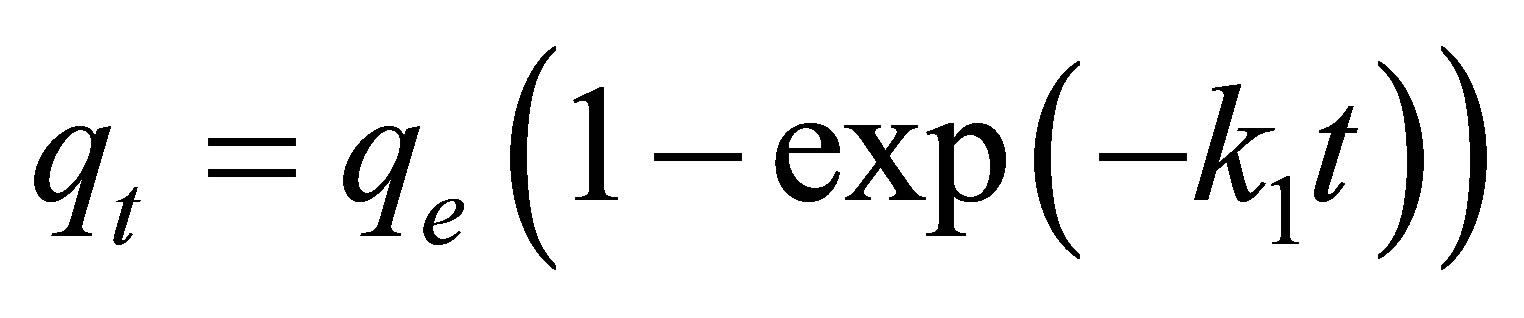 (3)
(3)
 (a)
(a) (b)
(b)
Figure 4. Effect of adsorbent dosage on the adsorption efficiency of dye complex onto AC1 and AC2 (initial dye concentration 220 mg/L, dye solution volume 25 mL).
Pseudo second-order kinetic model:
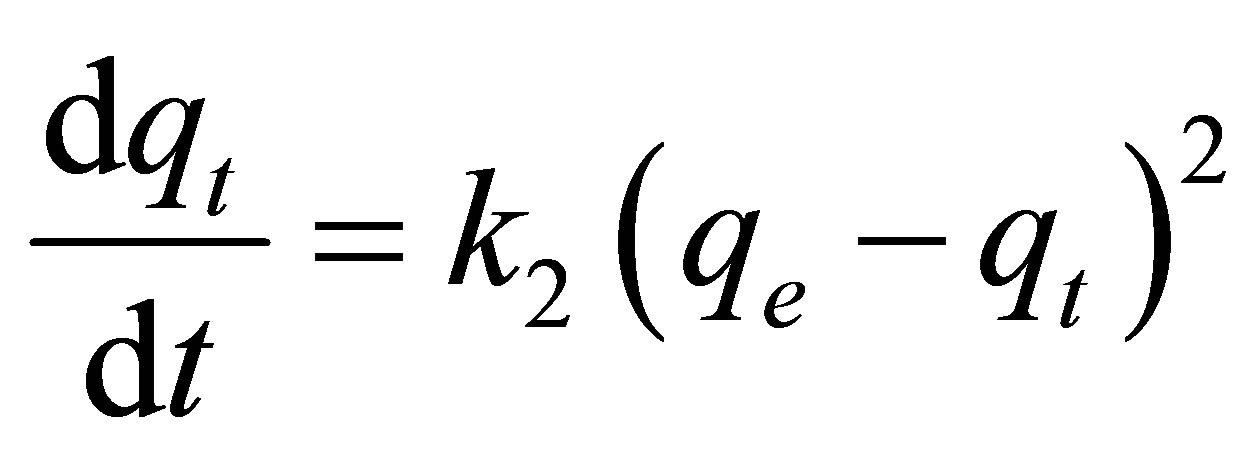 (4)
(4)
 (5)
(5)
Pore diffusion model:
 (6)
(6)
where qe and qt (mg/g carbon) are the amount of dye adsorbed at equilibrium and at any time t (min), respecttively, k1 (min−1) and k2 (g/mg-min) are the rate constants of the pseudo first-order and pseudo second-order model, respectively. De is the effective pore diffusivity in cm2/s when the time t is in second, and Rp is the radius of the assumed spherical shape adsorbent, taken as 0.036 cm.
Table 3 lists the values of kinetic parameters of the
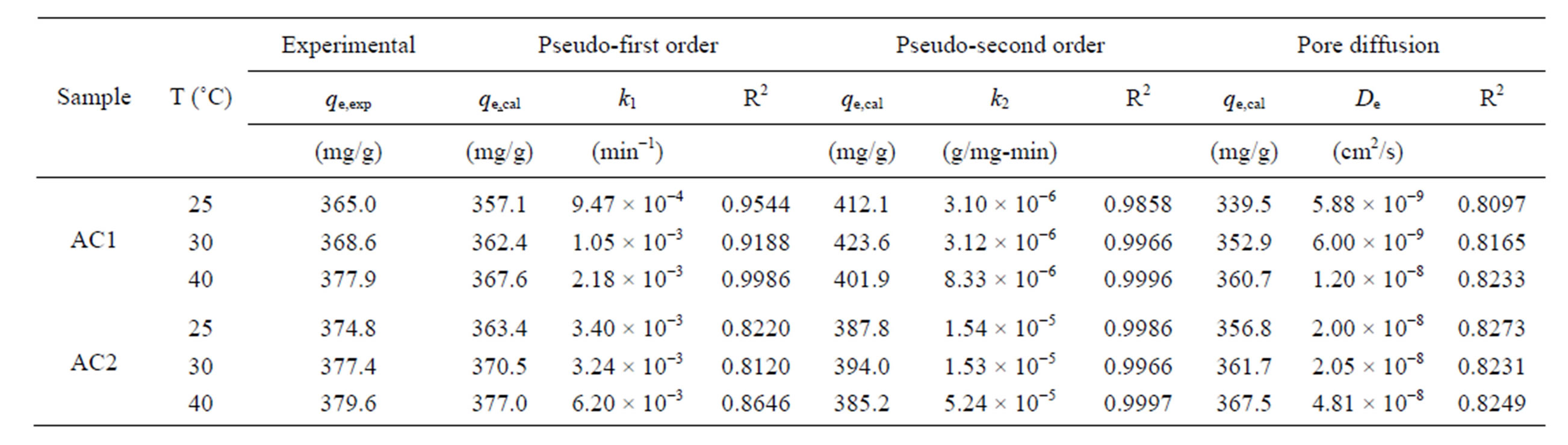
Table 3. Kinetic parameters for the adsorption of natural dye complex with eucalyptus based activated carbons.
 (a)
(a) (b)
(b)
Figure 5. Kinetics of natural dye complex adsorption using eucalyptus activated carbon (initial dye concentration 220 mg/L, dye solution volume 25 mL, carbon dosage 0.025 g).
three models for AC1 and AC2 obtained by a non-linear curve fitting, along with the values of regression coefficients (R2). Based on the values of R2, the pseudo second-order model appears to give the best fit for all conditions, followed by the pseudo first-order model and the pore diffusion model, respectively. The values of the rate constants, k1 and k2, were found to increase with increasing in the adsorption temperature concomitant with the favorable effect of increasing temperature on the amount of dye adsorbed. These results conform to the results of pore diffusion model in that the intraparticle diffusivity (De) also increases with the increase of temperature, indicating the increased transport rate of adsorbate molecules through the pore network to the adsorption sites. The values of De of the two eucalyptus activated carbons vary in the range from 5.88 × 10−9 to 4.81 × 10−8 cm2/s as compared with the values of 1.8 × 10−9 to 3.8 × 10−9 cm2/s of coconut shell activated carbon used to adsorb the same dye complex [25]. It appears that the dye molecules can transport at a faster rate in eucalyptus activated carbon than in coconut shell activated carbon and this should result from the difference in their internal pore structures.
3.4. Adsorption Isotherms
Langmuir isotherm equation [26], proposed based on the monolayer adsorption on a homogeneous surface (constant heat of adsorption), was used to describe the adsorption of dye complex onto activated carbon from eucalyptus wood. The equation reads
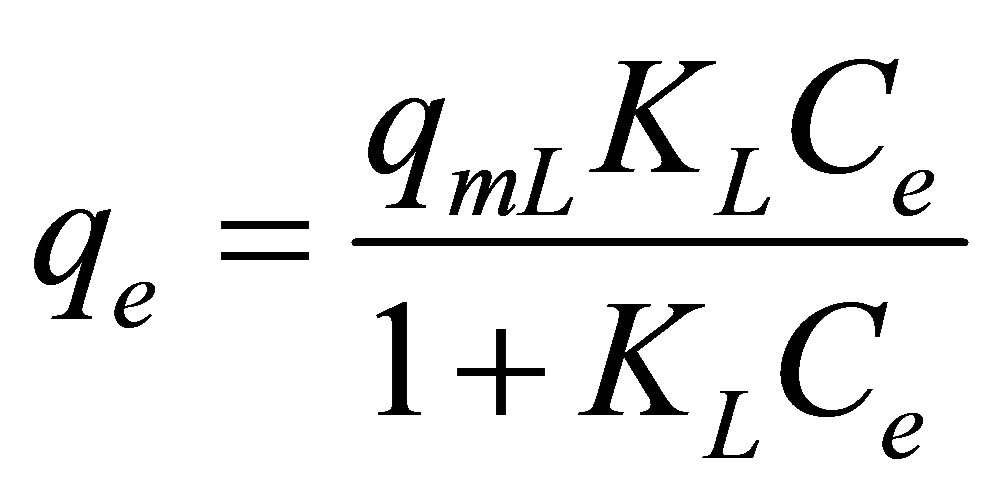 (7)
(7)
where Ce (mg/L) is the concentration of dye complex in the dye solution at equilibrium, qe (mg/g) is the amount of dye adsorbed at equilibrium, and qmL (mg/g) and KL (L/mg) are Langmuir constants related to maximum adsorption capacity and adsorption affinity, respectively.
Freundlich isotherm equation [27], developed based on the adsorption on a heterogeneous surface with distribution of adsorption energy, was also tested and is expressed by
 (8)
(8)
where KF and nF are Freundlich adsorption constants.
The adsorption isotherms of aluminium dye complex for the two activated carbons are displayed in Figure 6 as a function of temperature. It is clear that the dye adsorption is favored by an increase of adsorption temperature, indicating that the adsorption of this cationic dye complex by eucalyptus based activated carbon is an endothermic process. Since the dye complex is a large molecule with long benzene ring structure, it is hypothesized that with increasing in temperature the dye molecules can acquire high enough energy to arrange themselves and adsorbed more on the carbon surface to attain the most stable condition. The increase in adsorption
 (a)
(a)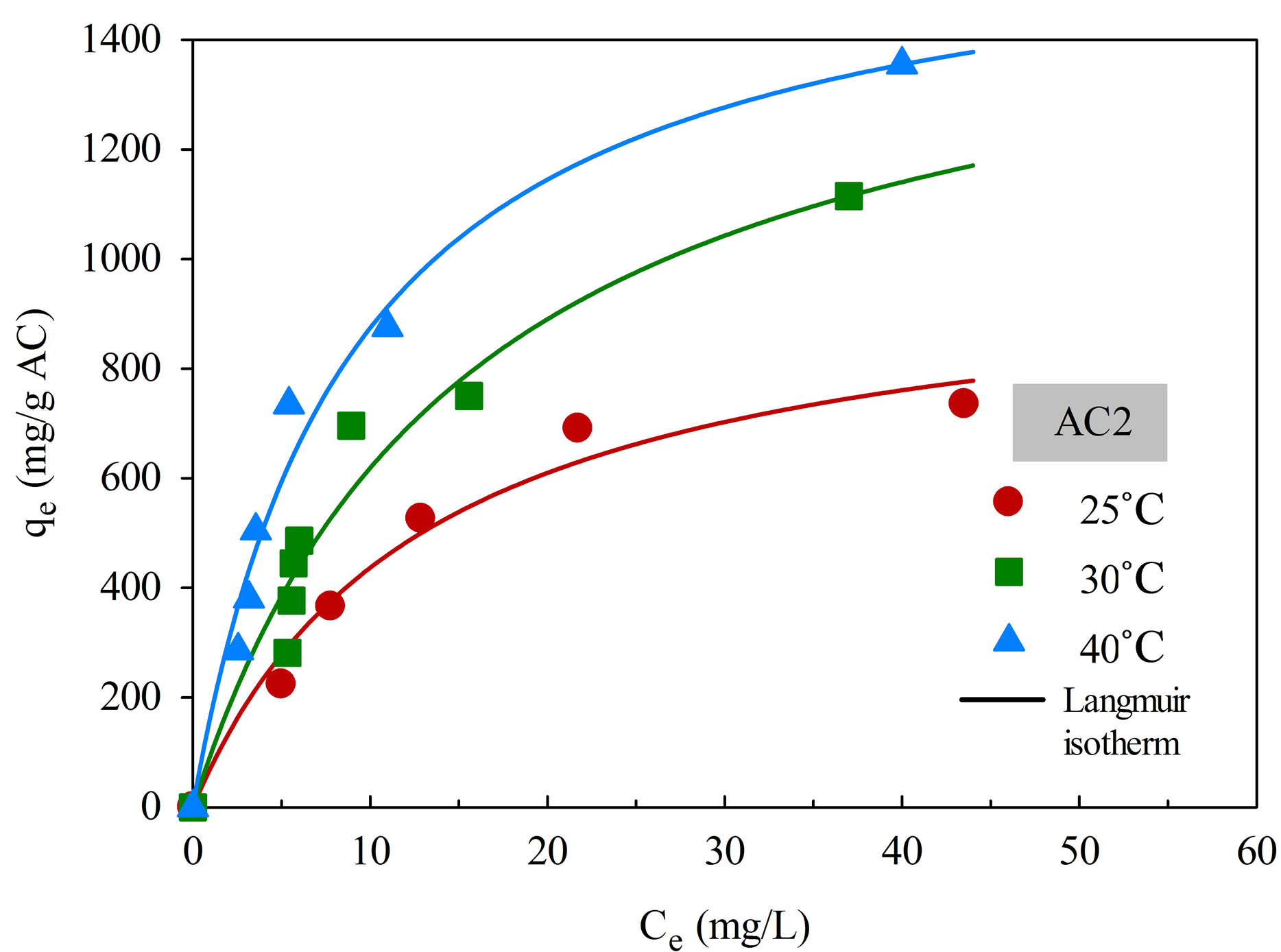 (b)
(b)
Figure 6. Adsorption isotherms of natural dye complex onto AC1 and AC2 as a function of temperature.
capacity with increasing temperature has been reported by several investigators for both the basic and acidic dyes [28,29].
There is also a clear indication that the adsorption capacity of AC2 is higher than that of AC1 at all temperatures. The adsorption of dye molecules on a hydrophobic activated carbon surface is by dispersive attraction between the π electrons of carbon graphitic plane and π electrons in the aromatic ring of the dye molecule [25].
As a result, activated carbon with large pore size, which facilitates the transport of large dye molecules, and with greater pore volume and surface area will be able to accommodate more adsorbed dye molecules on the carbon surface.
Table 4 shows the fitting parameters of the isotherm models. By considering the values of R2, Langmuir equation was found to give the better fit of isotherm data at all temperatures for both carbons, in comparison with the application of Freundlich equation. As expected, both qmL and KF, which reflect the adsorption capacity of activated carbon, are found to increase with increasing in temperature. There is also a general trend for KL, which is a measure of surface affinity, to increase with the temperature. However, there is no definite trend as to the effect of temperature on the value of nF which indicates the degree of surface heterogeneity and the non-linearity of the isotherm.
3.5. Adsorption Thermodynamics
Thermodynamic parameters of dye adsorption process including the standard enthalpy (ΔHo), standard free energy (ΔGo) and standard entropy (ΔSo) can be obtained from the following equations by plotting KL against 1/T on a semi-log scale [30],
 (9)
(9)
where R (8.314 J/mol-K) is the universal gas constant, T (K) is the absolute solution temperature, and KL (L/mg) is the Langmuir affinity constant. The slope and intercept of the straight line plot are used to calculate ΔHo and

Table 4. Parameters of Langmuir and Freundlich equations for dye complex adsorption with eucalyptus activated carbons.
ΔSo, respectively. ∆Go is calculated using the following relation:
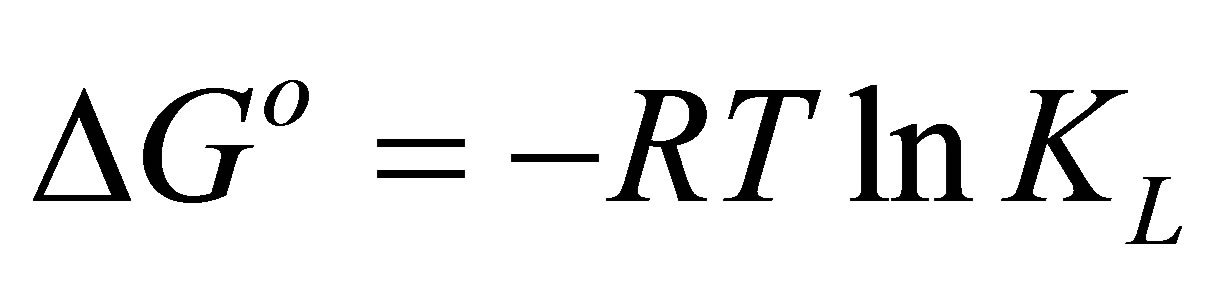 (10)
(10)
Arrhenius equation is applied to examine the effect of temperature on the rate constant, k2, of the pseudo second-order kinetic model. The equation is in the following form
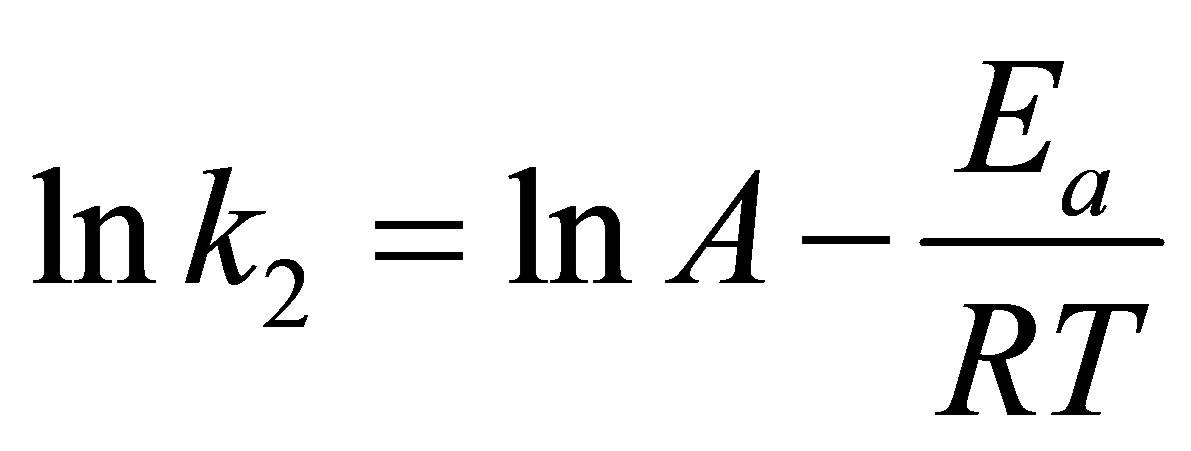 (11)
(11)
where k2 (g/mg-min) is the rate constant of the pseudo second-order model, Ea (kJ/mol) is the Arrhenius activetion energy of adsorption and A is the Arrhenius preexponential factor in g/mg-min.
Table 5 lists the derived thermodynamic parameters for the dye adsorption process. The positive values of Ea and ∆Ho indicate, respectively, that the adsorption is an activated process and the adsorption of the dye complex by eucalyptus activated carbon in this work is an endothermic process. The positive value of ∆So indicates the affinity of the dye complex towards AC1 and AC2 and the increasing randomness at the solid-solution interface during the adsorption process. The negative free energy change (∆Go < 0) indicates that dye complex adsorption is a spontaneous and favorable process at all temperatures studied.
4. Conclusion
The results from this study showed that two activated carbons (AC1 and AC2) prepared from eucalyptus wood, with surface area and pore volume of 738 m2/g and 0.39 cm3/g and 921 m2/g and 0.53 cm3/g, respectively, are effective for the removal of residual natural dye of [Al(brazilein)2]+ from silk dyeing process. It was found that the adsorption efficiency of this dye complex was dependent on adsorption time, porous properties of activated carbon used, adsorbent dosage and temperature of solution. The adsorption kinetics of this dye was best described by the pseudo second-order model, while equilibrium adsorption isotherms were best fitted with

Table 5. Thermodynamic parameters for the adsorption of dye complex with eucalyptus activated carbons.
Langmuir isotherm equation. The maximum adsorption capacities at 25˚C, 30˚C and 40˚C were 718.7, 1240.4 and 1139.5 mg/g, and 1010.5, 1586.1 and 1659.0 mg/g for AC1 and AC2, respectively. The positive adsorption enthalpies for the removal of this dye complex were 105.3 and 55.6 kJ/mol for AC1 and AC2, respectively, indicating that the adsorption of this natural dye is an endothermic process.
5. Acknowledgements
The financial support of this work from Suranaree university of Technology is gratefully acknowledged.
REFERENCES
- K. Wongsooksin, S. Rattanaphani, M. Tangsathtikulchai, V. Rattanaphani and J. Bremner, “Study of an Al(III) Complex with the Plant Dye Brazilein from Ceasalpinia sappan Linn.,” Suranaree Journal of Science and Technology, Vol. 15, No. 2, 2008, pp. 159-165.
- G. Ciardelli, L. Corsi and M. Marcucci, “Membrane Separation for Wastewater Reuse in the Textile Industry,” Resources, Conservation and Recycling, Vol. 31, No. 2, 2001, pp. 189-197. doi:10.1016/S0921-3449(00)00079-3
- G. R. P. Malpass, D. W. Miwa, S. A. S. Machado and A. J. Motheo, “Decolourisation of Real Textile Waste using Electrochemical Techniques: Effect of Electrode Composition,” Journal of Hazardous Materials, Vol. 156, No. 1- 3, 2008, pp. 170-177. doi:10.1016/j.jhazmat.2007.12.017
- A. Alinsafi, M. Khemis, M. N. Pons, J. P. Leclerc, A. Yaacoubi, A. Benhammou and A. Nejmeddine, “Electro-Coagulation of Reactive Textile Dyes and Textile Wastewater,” Chemical Engineering and Processing: Process Intensification, Vol. 44, No. 4, 2005, pp. 461-470. doi:10.1016/j.cep.2004.06.010
- K. Kumari and T. E. Abraham, “Biosorption of Anionic Textile Dyes by Nonviable Biomass of Fungi and Yeast,” Bioresource Technology, Vol. 98, No. 9, 2007, pp. 1704- 1710. doi:10.1016/j.biortech.2006.07.030
- T. Akar, A. S. Ozcan, S. Tunali and A.Ozcan, “Biosorption of a Textile Dye (Acid Blue 40) by Cone Biomass of Thuja orientalis: Estimation of Equilibrium, Thermodynamic and Kinetic Parameters,” Bioresource Technology, Vol. 99, No. 8, 2008, pp. 3057-3065. doi:10.1016/j.biortech.2007.06.029
- A. R. Khataee, F. Vafaei and M. Jannatkhah, “Biosorption of Three Textile Dyes from Contaminated Water by Filamentous Green Algal Spirogyra sp.: Kinetic, Isotherm and Thermodynamic Studies,” International Biodeterioration & Biodegradation, Vol. 83, 2013, pp. 33-40. doi:10.1016/j.ibiod.2013.04.004
- P. S. Kumar, S. Ramalingam, C. Senthamarai, M. Niranjanaa, P. Vijayalakshmi and S. Sivanesan, “Adsorption of Dye from Aqueous Solution by Cashew Nut Shell: Studies on Equilibrium Isotherm, Kinetics and Thermodynamics of Interactions,” Desalination, Vol. 261, No. 1-2, 2010, pp. 52-60. doi:10.1016/j.desal.2010.05.032
- N. M. Mahmoodi, B. Hayati, M. Arami and C. Lan, “Adsorption of Textile Dyes on Pine Cone from Colored Wastewater: Kinetic, Equilibrium and Thermodynamic Studies,” Desalination, Vol. 268, No. 1-3, 2011, pp. 117- 125. doi:10.1016/j.desal.2010.10.007
- C. Pelekani and V. L. Snoeyink, “Competitive Adsorption between Atrazine and Methylene Blue on Activated Carbon: The Importance of Pore Size Distribution,” Carbon, Vol. 38, No. 10, 2000, pp. 1423-1436. doi:10.1016/S0008-6223(99)00261-4
- Y. Guo, S. Yang, W. Fu, J. Qi, R. Li, Z. Wang and H. Xu, “Adsorption of Malachite Green on Microand Mesoporous Rice Husk-based Active Carbon,” Dyes and Pigments, Vol. 56, No. 3, 2003, pp. 219-229. doi:10.1016/S0143-7208(02)00160-2
- R. L. Tseng and S. K. Tseng, “Pore Structure and Adsorption Performance of the KOH-Activated Carbons Prepared from Corncob,” Journal of Colloid and Interface Science, Vol. 287, No. 2, 2005, pp. 428-437. doi:10.1016/j.jcis.2005.02.033
- C. Tangsathitkulchai, Y. Ngernyen and M. Tangsathitkulchai, “Surface Modification and Adsorption of Eucalyptus Wood-based Activated Carbon: Effects of Oxidation Treatment, Carbon Porous Structure and Activation Method,” Korean Journal of Chemical Engineering, Vol. 26, No. 5, 2009, pp. 1341-1352. doi:10.1007/s11814-009-0197-4
- F. Rouquerol, J. Rouquerol and K. Sing, “Adsorption by Powders and Porous Solids: Principles, Methodology and Applications,” Academic Press, San Diego, 1999.
- K. Wongsooksin, “Adsorption of Homoisoflavonoid and Extracted Dye from Heartwood of Ceasalpinia sappan Linn. On Silk Fibers and Treatment of Dye Effluent by Activated Carbons,” Ph.D. Thesis, Suranaree University of Technology, 2008.
- C. F. Chang, C. Y. Chang and W. T. Tsai, “Effects of Burn-Off and Activation Temperature on Preparation of Activated Carbon from Corn Cob Agrowaste by CO2 and Steam,” Journal of Colloid and Interface Science, Vol. 232, No. 1, 2000, pp. 45-49. doi:10.1006/jcis.2000.7171
- W. M. A. W. Daud and W. S. W. Ali, “Comparison on Pore Development of Activated Carbon Produced from Palm Shell and Coconut Shell,” Bioresource Technology, Vol. 93, No. 1, 2004, pp. 63-69. doi:10.1016/j.biortech.2003.09.015
- T. Yang and A. C. Lua, “Characteristics of Activated Carbons Prepared from Pistachio-Nut Shells by Physical Activation,” Journal of Colloid and Interface Science, Vol. 267, No. 2, 2003, pp. 408-417. doi:10.1016/S0021-9797(03)00689-1
- J. Colman, “Acacia-Wattle,” 2001. http://www.janinesgarden.com/plants/A/acacia.html
- M. Valix, W. H. Cheung and G. McKay, “Preparation of Activated Carbon using Low Temperature Carbonisation and Physical Activation of High Ash Raw Bagasse for Acid Dye Adsorption,” Chemosphere, Vol. 56, No. 5, 2004, pp. 493-501. doi:10.1016/j.chemosphere.2004.04.004
- D. Suteu and T. Malutan, “Industrial Cellolignin Wastes as Adsorbent for Removal of Methylene Blue Dye from Aqueous Solutions,” BioResources, Vol. 8, No. 1, 2013, pp. 427-446.
- Y. S. Ho and G. McKay, “Kinetic Models for the Sorption of Dye from Aqueous Solution by Wood,” Process Safety and Environmental Protection, Vol. 76, No. 2, 1998, pp. 183-191. doi:10.1205/095758298529326
- Y. S. Ho and G. McKay, “Pseudo-Second Order Model for Sorption Processes,” Process Biochemistry, Vol. 34, No. 5, 1999, pp. 451-465. doi:10.1016/S0032-9592(98)00112-5
- D. D. Do, “Analysis of Adsorption Kinetics in a Single Homogeneous Particle,” In: D. D. Do, Ed., Adsorption Analysis: Equilibria and Kinetics, Imperial College Press, 1998, pp. 521-545.
- M. Tangsathitkulchai, C. Tangsathitkulchai, K. Wongsooksin and S. Chuyingsakuntip, “Removal of Residual Aluminium-Dye Complex and Aluminium Ion from Spent Natural-Dye Solution Using Activated Carbons,” Engineering Journal, Vol. 16, No. 5, 2012, pp. 29-44. doi:10.4186/ej.2012.16.5.29
- I. Langmuir, “Adsorption of Gases on Plain Surfaces of Glass Mica Platinum,” Journal of American Chemical Society, Vol. 40, No. 9, 1918, pp. 1361-1403. doi:10.1021/ja02242a004
- H. Freundlich, “Adsorption Solution,” Zeitschrift für Physikalische Chemie, Vol. 57, 1906, pp. 384-470.
- M. F. R. Pereira, S. F. Soares, J. J. M. Orfao and J. L. Figueiredo, “Adsorption of Dyes on Activated Carbons: Influence of Surface Chemical Groups,” Carbon, Vol. 41, No. 4, 2003 pp. 811-821. doi:10.1016/S0008-6223(02)00406-2
- A. A. Attia, W. E. Rashwan and S. A. Khedr, “Capacity of Activated Carbon in the Removal of Acid Dyes Subsequent to Its Thermal Treatment,” Dyes and Pigments, Vol. 69, No. 3, 2006, pp. 128-136. doi:10.1016/j.dyepig.2004.07.009
- K. Li, Z. Zheng, X. Huang, G. Zhao, J. Feng and J. Zhang, “Equilibrium, Kinetic and Thermodynamic Studies on the Adsorption of 2-Nitroaniline onto Activated Carbon Prepared from Cotton Stalk Fibre,” Journal of Hazardous Materials, Vol. 166, No. 1, 2009, pp. 213-220. doi:10.1016/j.jhazmat.2008.11.007
NOTES
*Corresponding author.

