Journal of High Energy Physics, Gravitation and Cosmology
Vol.03 No.01(2017), Article ID:72213,8 pages
10.4236/jhepgc.2017.31004
Examination of Schrodinger Equation in Pre-Planckian Space-Time Early Universe
Andrew Walcott Beckwith
Physics Department, College of Physics, Chongqing University Huxi Campus, Chongqing, China

Copyright © 2017 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: August 29, 2016; Accepted: November 20, 2016; Published: November 23, 2016
ABSTRACT
We look at the Vuilli (1999) write up of a generalized Schrodinger equation with its Ricci scalar inclusion, in curved space-time. This has a simplified version in Pre-Planckian regime, which leads to comparing a resultant admissible wave function with Bohmian reformulations of quantum physics. As was done earlier, we compare this result with a formulation of a modified “Poisson” equation from Poissons and Will from 2014, and then use inflaton physics. The resulting inflaton is then compared to the wave functional in the first part of this document.
Keywords:
Ricci Tensor, Schrodinger Equation, Modified Poisson Equation, Massive Gravity, Inflaton Physics

1. Vuilli Treatment of Schrodinger Equation for Curved Space-Time
Here, we bring up [1] , and a reset of the Schrodinger equation in early space-time, with curvature.
In [1] we start with
 (1)
(1)
Through the following substitutions,
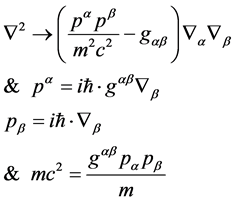 (2)
(2)
Then, after more derivation [1] obtained, with using the Ricci tensor  the following result: [2]
the following result: [2]
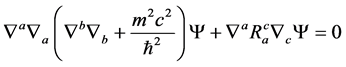 (3)
(3)
2. Simplifying Equation (3) in Pre-Planckian Space-Time
We will re write Equation (3) to read as follows, with the result that in Pre-Planckian space-time
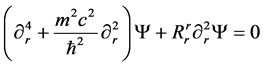 (4)
(4)
Ricci tensor 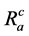 in this setting becomes a constant, and is part of how the wave function evolves, and our candidate wave functional takes the form of
in this setting becomes a constant, and is part of how the wave function evolves, and our candidate wave functional takes the form of
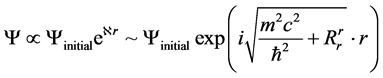 (5)
(5)
We will be identifying what to put into [3] , i.e., the Ricci scalar as given in Pre- Planckian space-time
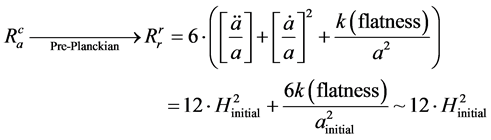 (6)
(6)
We are assuming that the term  approaches zero in Pre-Planckian space- time. Obviously if it did not, the last term
approaches zero in Pre-Planckian space- time. Obviously if it did not, the last term 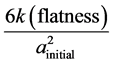 would be dominant.
would be dominant.
Having said this, with an evolutionary equation statement as to the phase value of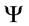 , it is time to look at the initial
, it is time to look at the initial  and to try to learn some physics from it.
and to try to learn some physics from it.
3. Defining the Initial Value Yinitial of Equation (5)
In order to do this, it may be useful to look at the classical degeneracy argument for forming , and the reference by Rubakov may be useful for this [4] i.e. using a false vacuum analogy, we can write, if q is a generalized space-time unit of “length”, and we examine a quartic potential, i.e. look at
, and the reference by Rubakov may be useful for this [4] i.e. using a false vacuum analogy, we can write, if q is a generalized space-time unit of “length”, and we examine a quartic potential, i.e. look at
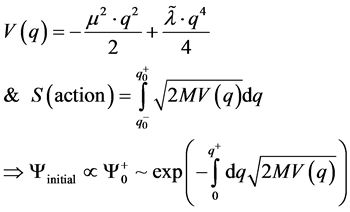 (7)
(7)
Now, use the usual given
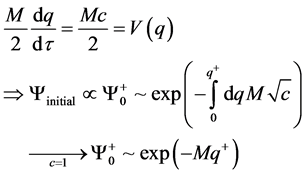 (8)
(8)
If using Ng infinite quantum statistics, [5] , and a non zero massive graviton mass (massive gravity) [6]
 (9)
(9)
And if we have here that 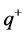 is in some sense proportional to length less than or equal to Planck length, the astonishing conclusion is that Equation (8) would probably be biased toward a low ( nonzero) entropy count, which would mean for finite initial entropy, connected with information transfer, that we would through Equation (8) and Equation (9) have a bias toward initially low, say 105 or so initial entropy, as a way to quantify the input into the formation of an initial wavefunction, using entropy as equivalent to information as given by Lloyd [7] .
is in some sense proportional to length less than or equal to Planck length, the astonishing conclusion is that Equation (8) would probably be biased toward a low ( nonzero) entropy count, which would mean for finite initial entropy, connected with information transfer, that we would through Equation (8) and Equation (9) have a bias toward initially low, say 105 or so initial entropy, as a way to quantify the input into the formation of an initial wavefunction, using entropy as equivalent to information as given by Lloyd [7] .
4. Comparing the Inputs into Equation (5), Equation (6), Equation (8) and Equation (9) against Force against Individual “Gravitons” in the Pre-Planckian Space-Time
We will go to the [3] reference, page 85, in order to look at a change in the stress energy tensor,
 (10)
(10)
Using this, and stating that in the Pre-Planckian regime of space-time due to [8] , that

Here, we have that the initial volume 
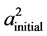

Having said that, let us use a semi classical argument as to why the radii would not go to zero, even in Pre-Planckian space-time. This would be to insure that 
5. What Is Important about the Modified Poissons Equation [12] ? Getting a Non Zero Initial DV(3)
We will first of all refer to two necessary and sufficient conditions for the onset of a massive graviton given in [13] , and combined with Padmanablan’s reference [12] .
i.e. what we will be doing is to re do the reference calculations given in [13] with

Here, we will be using in the Pre-Planckian potential the inputs from the data usually associated with [12]

In other words, we will be using the inflation given by

If so, then

Then, after algebra, we have the following, from [14]

The quadratic Equation this engenders is, how to say

A candidate for the density functional will come next, with the way of obtaining a critical value for r is given by [14] as follows, i.e. if

As far as applications to: [1]

This would, lend itself to a quadratic equation for r, and the cube of r would be proportional to 
6. Comparing the Results of a Non Zero DV(3) in Pre-Planckian Wave Functional for Equation (8) against De Broglie-Bohmian Path of a Wave Functional
What we are examining if our qualitative argument which in sum yields a Pre- Planckian wavefunction as compared against the construction given in [15] which is in spirit comparable, up to a point with [16]
According to [15] we would have

Here, 

Here, if we use


Here, M would be given by Equation (9), i.e. and V were given by Equation (18) we would find to a point that

i.e. the term 

7. Conclusion, Overlap with the Bohmian Quantum Picture of Physics If Equation (24) Is Confirmed for Pre-Planckian Space-Time
The question to ask, is the following true? This has to be confirmed rigorously.

The significance of proving or falsifying Equation (24) will in the end be part of future data analysis which should not contravene [17] [18] [19] . i.e. the experimentally implied limits should be adhered to and studied rigorously.
Furthermore, we have that analysis of Equation (24) may be in tandem with analysis of the Corda paper [20] as to if gravity is possibly scalar-tensor, an extension of GR (possibly with some semi classical treatment of presumed quantum gravity formulations), or something else.
Finally, since our paper is with respect to relic conditions, if so, then if we are to use a variant of interferometer methods, reference [21] and [22] if relic conditions are observable, via some form of space bound system, may allow us to with refinements get enough control of stochastic noise contamination of GW and the foot print of massive gravity to come up with confirmable data sets as to early universe conditions. With luck, with considerable refinement of instrumentation, we may also be able to get experimental confirmation of [23] and its predictions as to inflaton physics and possibly massive gravity.
Acknowledgements
This work is supported in part by National Nature Science Foundation of China grant No. 11375279.
Cite this paper
Beckwith, A.W. (2017) Examination of Schrodinger Equation in Pre-Planckian Space-Time Early Universe. Journal of High Energy Physics, Gravitation and Cosmology, 3, 21-28. http://dx.doi.org/10.4236/jhepgc.2017.31004
References
- 1. Vuille, C. (1999) Schrodingers’ Equation in General Relativity. In: Burgess, C.P. and Myers, R., Eds., General Relativity and Relativistic Astrophysics, Eighth Canadian Conference, AIP Conference Proceedings, 493, Melville, New York, 243-246.
- 2. Carmelli, M. (1982) Classical Fields, General Relativity and Gauge Theory. Wiley Interscience, New York.
- 3. Scott, R. (2016) A Student Manual for A First Course in General Relativity. Cambridge University Press, Cambridge, UK.
- 4. Rubakov, V. (2002) Classical Theory of Gauge Fields. Princeton University Press, Princeton.
- 5. Ng, Y.J. (2008) Spacetime Foam: From Entropy and Holography to Infinite Statistics and Nonlocality. Entropy, 10, 441-461.
https:/doi.org/10.3390/e10040441 - 6. Goldhaber, A. and Nieto, M. (2010) Photon and Graviton Mass Limits. Reviews of Modern Physics, 82, 939-979.
http://arxiv.org/abs/0809.1003
https:/doi.org/10.1103/RevModPhys.82.939 - 7. Lloyd, S. A Theory of Quantum Gravity Based on Quantum Computation.
https://arxiv.org/abs/quant-ph/0501135 - 8. Beckwith, A. (2016) Gedanken Experiment for Refining the Unruh Metric Tensor Uncertainty Principle via Schwarzschild Geometry and Planckian Space-Time with Initial Nonzero Entropy and Applying the Riemannian-Penrose Inequality and Initial Kinetic Energy for a Lower Bound to Graviton Mass (Massive Gravity). Journal of High Energy Physics, Gravitation and Cosmology, 2, 106-124.
https:/doi.org/10.4236/jhepgc.2016.21012 - 9. Schwartz, B. (2011) A First Course in General Relativity. 2nd Edition, Cambridge University Press, Cambridge, United Kingdom.
- 10. Camara, C.S., de Garcia Maia, M.R., Carvalho, J.C. and Lima, J.A.S. (2004) Nonsingular FRW Cosmology and Non Linear Dynamics. Version 1, February 12.
Arxiv astro-ph/0402311. - 11. Beckwith, A. (2016) Thermodynamics and the Energy of Gravity Waves, GW’s, as a Consequence of Non Linear Electrodynamics, NLED, Leading to an Initial Temperature and Strain h for Gravity Waves, GW, at the Start of Inflation. Journal of High Energy Physics, Gravitation and Cosmology, 2, 98-105.
https:/doi.org/10.4236/jhepgc.2016.21011 - 12. Padmanabhan, T. (2005) Understanding Our Universe, Current Status and Open Issues. In: Ashatekar, A., Ed., 100 Years of Relativity, Space-Time Structure: Einstein and Beyond, World Scientific Publishing, Singapore, 175-204.
http://arxiv.org/abs/gr-qc/0503107
https:/doi.org/10.1142/9789812700988_0007 - 13. Poisson, E. and Will, C. (2014) Gravity: Newtonian, Post Newtoninan, Relativistic. Cambridge University Press, Cambridge.
https:/doi.org/10.1017/CBO9781139507486 - 14. Beckwith, A. (2016) Examination of Sufficient Conditions for Forming Mass of “Massive Graviton”, from Early Universe.
- 15. Licata, I. and Fiscaletti, D. (2014) Quantum Potential: Physics, Geometry, and Algebra. Springer-Verlag, New York.
https:/doi.org/10.1007/978-3-319-00333-7 - 16. Beckwith, A. (2016) Gedanken Experiment for Looking at δgtt for Initial Expansion of the Universe and Influence on HUP via Dynamical Systems, with Positive Pre-Planckian Acceleration. Journal of High Energy Physics, Gravitation and Cosmology, 2, 531-545.
https:/doi.org/10.4236/jhepgc.2016.24046 - 17. Abbott, B., et al. (2016) Observation of Gravitational Waves from a Binary Black Hole Merger. LIGO Scientific Collaboration and Virgo Collaboration. Physical Review Letters, 116, Article ID: 061102.
https:/doi.org/10.1103/physrevlett.116.061102 - 18. Abbott, B., et al. (2016) GW151226: Observation of Gravitational Waves from a 22-Solar-Mass Binary Black Hole Coalescence. LIGO Scientific Collaboration and Virgo Collaboration. Physical Review Letters, 116, Article ID: 241103.
https:/doi.org/10.1103/physrevlett.116.241103 - 19. Abbott, B., et al. (2016) Tests of General Relativity with GW150914. Physical Review Letters, 116, Article ID: 221101.
https://arxiv.org/pdf/1602.03841.pdf
https:/doi.org/10.1103/physrevlett.116.221101 - 20. Corda, C. (2009) Interferometric Detection of Gravitational Waves: The Definitive Test for General Relativity. International Journal of Modern Physics D, 18, 2275-2282.
https://arxiv.org/abs/0905.2502
https:/doi.org/10.1142/S0218271809015904 - 21. Willke, B., et al. (2006) Stabilized High Power Laser for Advanced Gravitational Wave Detectors. Journal of Physics: Conference Series, 32, 270.
http://iopscience.iop.org/article/10.1088/17426596/32/1/040/meta;jsessionid=B072B9D72E7EB4F993D70061EEE365CF.c5.iopscience.cld.iop.org
https:/doi.org/10.1088/1742-6596/32/1/040 - 22. Flaminio, R., Franc, J., Michel, C., Morgado, N., Pinard, L. and Sassolas, B. (2010) A Study of Coating Mechanical and Optical Losses in View of Reducing Mirror Thermal Noise in Gravitational Wave Detectors. Classical and Quantum Gravity, 27, Article ID: 084030.
https:/doi.org/10.1088/0264-9381/27/8/084030 - 23. Corda, C. (2012) Gravity’s Primordial Breath. Electronic Journal of Theoretical Physics, 9, 1-10.
http://www.ejtp.com/articles/ejtpv9i26p1.pdf

