Journal of High Energy Physics, Gravitation and Cosmology
Vol.02 No.01(2016), Article ID:62524,8 pages
10.4236/jhepgc.2016.21004
The Geomagnetic Field
Angel Fierros Palacios
Instituto de Investigaciones Eléctricas, División de Energías Alternas, Mexico City, México

Copyright © 2016 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 4 June 2015; accepted 28 December 2015; published 31 December 2015
ABSTRACT
In this paper a solution to the problem of the self-generated magnetic field of the Earth is proposed. The solution is based on the existence of a steady-state current distribution localized in some region inside the convective zone of the planet, constituted by the fluid Outer Core. The magnitude of the self-generated magnetic field is obtained and it is shown to be a dipolar field.
Keywords:
The Geomagnetic Field

1. Introduction
In order to properly pose the problem on the origin and structure of the Geomagnetic Field, and according to the arguments that follow, it is proposed that the origin may be located in the Outer Core and not in the Inner Core, as commonly believed. According to the specialized literature [1] , the Earth is composed by the Crust, the Mantle and the Central Core. The Crust is the thin outer region of the Earth. The Mantle is a region that goes from the Crust to the Central Core. It is totally solid, although throughout geologic times it can behave as a plastic material.
On the other hand, the Central Core is usually divided into two regions, called the Outer Core and the Inner Core. There is enough evidence to prove that the Outer Core is a fluid, while the Inner Core is solid [2] .
This latter region resembles a sphere composed almost totally by high temperature molteniron, possibly constant along all its volume. This region can be considered as a huge mass of isothermal molten iron.
Due to the fact that this hot mass is under great pressure, the value of its density is very big, almost near that of the solid iron [2] . Thus it is very hard that under such conditions the necessary temperature differences for the production of convective currents can be reached in this place.
On the other hand, the values of pressure, density and temperature in the Outer Core increase continuously from those at the surface of the planet to those at the Inner Core. Does, in the outer Core the proper conditions exist to generate the thermal gradients necessary to produce convective streams.
Consequently, it is being proposed here to consider the Outer Core as the convective zone of the planet, and that it is in this place where the origin of the Earth’s self-generated magnetic field can be located.
As in the case of gaseous star, it is assumed that the Geomagentic Field is generated by a steady-state current distribution localized in some region inside the convective zone, which is produced by a process of maximum ionisation. Moreover, due to the fact that the Outer Core is dragged along by the planet’s rotation, this region revolves around the terrestrial axis with a differential rotational velocity, due to the fact that it is composed by a very viscous fluid.
2. The Magnitude of the Self-Generated Magnetic Field
Let us consider the case of a huge mass of very viscous compressible and conducting fluid, isolated in space and with inwardly increasing values of pressure, density and temperature; that revolves around its own axis with rotational velocity v(x, t) and is under the influence of a magnetic field H(x, t). Here, x is the distance measured from any internal point to the center of the object, and t is the time.
Additionally, this huge concentration of matter is found distributed in a configuration that has spherical symetry.
The following equation is used to determine the dynamic state of this huge mass of fluid
 . (1)
. (1)
This last relation is the momentum balance equation of magnetohydrodynamics (MHD) [3] . In (1) f is the body force per unit mass, r (x, t) the mass density, and
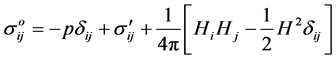 ; (2)
; (2)
are the components of the generalized stress tensor [3] , dij the components of the Kroenecker delta, p (x, t) the pressure and in the third term of the right hand side of equation (2), one has the components of Maxwell’s magnetic stress tensor [4] .
On the other hand
 , (3)
, (3)
are the components of the viscosity stress tensor, with h and z the coefficients of viscosity [3] [7] .
Let us consider that the above described object is the Earth’s Central Core. In this case, the rotational velocity of this central region, is not an explicit function of the variable x; due to the fact that v = v (l, t) with l the latitude.
Beside, one can suppose that H(x,t) is the self-generated magnetic field by the Earth. Since that object revolves around it’s own axis in such a way that the regime is steady, ¶v/¶t = 0, and then, the term on the left hand side of (1) is zero; that is to say,
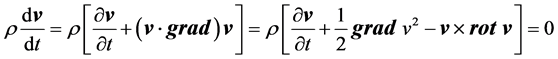 ;
;
where the definitions of hydrodynamic derivative [3] [7] and a well known formula in vector analysis [3] [10] were used.
Consequently, from (1) one gets the following result
 ; (4)
; (4)
because in that case, the bodyforce per unit mass is g, the acceleration of terrestrial gravity. From the last equation, and due to the fact that ¶/¶xj = ¶/¶xidij, the following result is obtained
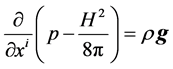 ; (5)
; (5)
due to that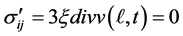 . The last relation is the equation that governs the state of equilibrium of the Earth’s Central Core, which in this case is magneto mechanical. Equation (5) can be integrated considering that r = r (R, t), with R the Central Core radius, to obtain the following result
. The last relation is the equation that governs the state of equilibrium of the Earth’s Central Core, which in this case is magneto mechanical. Equation (5) can be integrated considering that r = r (R, t), with R the Central Core radius, to obtain the following result
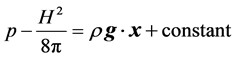 . (6)
. (6)
From the specialized literature [2] one obtains that the pressure is given by the next expression
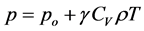 ; (7)
; (7)
where CV is the specific heat at constant volume, T the temperature, g the thermodynamic Grüneisen parameter [5] [6] and po is an initial ambient pressure [2] [5] [6] such that it is possible to assume that the hydrostatic equation is satisfied [7] ; i.e.,
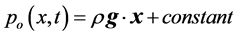 . (8)
. (8)
According to (7) and (8), one obtains from (6) that
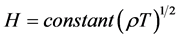 ; (9)
; (9)
where
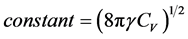 . (10)
. (10)
Consequently, it can be said that the magnitude of the geomagnetic field in the inner regions of the Earth varies like the square root of the product of the mass density and the temperature; both calculated at those regions.
3. The Structure of the Geomagnetic Field
It is considered that within the theoretical framework of MHD, H = B [3] [4] , and then the Earth’s self-generated magnetic field satisfies the basic laws of magnetostatics, which in their differential form are the following relationships [8]
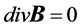 , (11)
, (11)
and
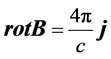 ; (12)
; (12)
where j is the steady-state current distribution localized in some region of the convective zone, and c is the velocity of light in empty space.
According to (11), B(x) must be the curl of some vector field A(x), called the vector potential [8] ; that is,
 . (13)
. (13)
For a steady-state current distribution localized in a relative small region of space, the vector potential is given by the following relation [8]

where 
Expanding the denominator of (14) in powers of 

The fact that j is a localized divergence less steady-state current distribution, allows simplification and transformation of (15). In fact, it can be shown that [8] [9]

Thus, the first term in (15), corresponding to the monopole term in the electrostatic expansion is therefore absent. The integral in the second term in (15) can then be written as follows [8] [9]

It is customary to define the magnetic moment density, or magnetization as [8] [9]

and its integral as the magnetic moment m; that is

Then, the vector potential from the second term in (15) is the magnetic dipole vector potential

This is the lowest non-vanishing term in the expansion of A for a localized steady-state current distribution. The corresponding magnetic induction B can be calculated directly by evaluating the curl of the last equation [8] [9] ; that is,

where n is a unit vector in the direction x. The magnetic induction B has exactly the form of the field of a dipole. Far away from the localized steady-state current distribution, the magnetic induction B is that of a magnetic dipole of dipole momentum given by (17).
4. Changes of Polarity of the Geomagnetic Field
From geological formation like frozen lava flows or sediment allayers, it is frequently found to have repeated alterations of magnetic polarity; apparently due to a process of ionic reordering in the Outer Core of the Earth [2] . That mechanism appears to be responsible of reversal of the Geomagnetic Field; the last of which occurred 700,000 years ago [2] .
In order to give a possible explanation of such mechanism, let us consider the average field produced by a system of charges each one of them with charge q, in steady motion, at large distances from the point where the field is calculated. It can be demonstrated that the magnetic moment of that system is given by the following expression [3] .

Where c is the velocity of light in the empty space, r the vector radius of the point where the field is calculated, and v = dr/dt is the average velocity of each charge. On the other hand, and according to (19)

where r is the distance from the Outer Core to the Earth surface, and we considered that n = 1. From the previous two equations, we have that

The polarity of the magnetic induction is close related with the sign of the system of charges. Thus, in one geological cycle there could be surges of ionized particles mainly of negative charge, and in the following, mainly of positive charges. Then the polarity of the Geomagnetic Field to be as expected, according to the kind of charged particles in each cycle. This is enough to give a heuristic explanation of the process of changes of polarity of the magnetic induction of the Earth.
5. Secular Variation and the Westward Drift
The Geomagnetic field can be represented by a magnetic dipole situated in the Earth’s Outer Core, considered as the convective zone of the Planet; and having a dipole moment with its axis inclined about 11˚ to the Earth’s geographic axes. It has been known for over 400 years that undergoes a secular variation due to a steady progressive change in magnetic declination, or angle between magnetic north and geographic north [2] . That movement is due to a steady west ward drift of the Geomagnetic Field, which is closely related to the eccentric dipole position [2] .
Let’s consider the Outer Core as a charged body spinning with differential velocity, due to the fact that it is composed by a very viscous fluid, in the self-generated magnetic field. Further, it has a system of particles each one of them with charge q, and mass m, in steady motion with velocities
In order to propose a solution of that problem, let us consider the system of particles and its interaction with the self-generated magnetic field. The time rate of change of the total angular momentum of the system, is equal to the total impressed torque [15] ; so that

It will be assumed that all the particles have the same q/m ratio; in such a way that

where Q is the total charge, and m the total mass.
Thus, the total angular momentum of the system of particles is

with p = mv the linear momentum of that system.
As the field is uniform, there will be no net force on the system, but there will be a net torque, approximately given by [15]

where m is the magnetic moment of the system; so that

In Theoretical Physics, there is a unique relationship between the angular momentum of the system and its magnetic moment, given by the following expression [15] [16]

in such a way that the equation of motion is

This is the equation of motion for a constant vector which is rotating about the direction of B with an angular velocity

The motion is similar to what in Nuclear Physics, is called the Larmor precession, and the angular velocity is known as the Larmor frequency. The uniform precession of a system of charges in a magnetic field holds true provided the center of mass is at rest [15] . For any system of charged particles, therefore, the total angular momentum, and with it the magnetic moment, rotates with the angular velocity (30) around the direction of the field, while its absolute magnitude and the angle which it makes with this direction remain fixed. In other words, both vectors will undergo a Larmor precession, with the only requirement that all charges have the same q/m ratio. On the other hand, the Outer Core revolves around the geographic axis with a differential rotational velocity. The interaction between both independent movements has as a consequence the secular variation, due to a westward drift, of the Geomagnetic Field.
6. Conclusions
In the present paper, a fundamental hypothesis is made which assumes that the origin of the self-generated Geomagnetic Field may be located in the Outer Core, considered as the convective zone of the Earth. This geomagnetic field is produced by some special mechanism, like the one producing the self-generated magnetic field in all gaseous stars [9] . In fact, according to the density and temperature conditions, some region should exist in the convective zone that has a maximum of ionization.
The electrically charged particles are moved by the convective streams across that region, making their contribution to the steady-state current distribution localized, and move away being continuously replaced by other particles [9] .
Since this current distribution is produced by the high ionization in the region, and the process depends on the density and temperature conditions in that region, the magnitude of the self-generated dipolar Geomagnetic Field is a function of those variables [9] , as it can be easily seen from Equation (9).
Finally, the changes of polarity of the Geomagnetic Field apparently are due to a process of ionic reordering in the Outer Core, in such a way that in one geological cycle the magnetic induction has the (N-S) polatiry, and in the following the (S-N) polarity.
The Goemagnetic Field undergoes a secular variation due to a westward drift, which can be related with a combination of the Larmor precession of the total angular momentum, and also the magnetic moment of the system of charged particles, around the self-generated magnetic field, and the differential rotational movement of the Outer Core around the terrestrial axes, which is observed over large areas of the Earth.
Cite this paper
Angel FierrosPalacios, (2016) The Geomagnetic Field. Journal of High Energy Physics, Gravitation and Cosmology,02,33-40. doi: 10.4236/jhepgc.2016.21004
References
- 1. Bullen, E.K. (1979) El interior de la Tierra. El redescubrimiento de la Tierra. Consejo Nacional de Ciencia y Tecnología, México.
- 2. Stacey, F.D. (1977) Physics of the Earth. Second Edition. John Wiley & Sons. New York. Santa Barbara. Londo Sydney. Toronto.
- 3. Fierros Palacios, A. (2006) The Hamilton-Type Principle in Fluid Dynamics. Fundamentals and Applications to Mag- netohydrodynamics, Thermodynamics, and Astrophysics. Springer-Verlag, Wien.
- 4. Landau, L.D. and Lifshitz, E.M. (1960) Electrodynamics of Continuous Media. Addison-Wesley Publishing Co., London.
- 5. Landau, L.D. and Lifshitz, E.M. (1958) Statistical Physics. Pergamon Press LTD: London-Paris and Adisson-Wesley Publishing Co.
- 6. Callen, H.B. (1960) Thermodynamics. Jonh Wiley & Sons, Inc. NewYork. London Sydney.
- 7. Landau, L.D. and Lifshitz, E.M. (1959) Fluid Mechanics. Addison-Wesley Publishing Co., London.
- 8. Jackson, J.D. (1962) Classical Electrodynamics. John Wiley & Sons, Inc., New York, London. http://dx.doi.org/10.1063/1.3057859
- 9. Fierros Palacios, A. (2002) The Magnetic Field in the Stability of the Stars. Submitted.
- 10. Spigel, M.R. (1959) Vector Analysis and Introduction to Tensor Analysis. Shaum Publishing Co., New York.
- 11. Parker, E.N. (1955) Hidromagnetic Dynamo Models. Astrophysical Journal, 122, 293-314. http://dx.doi.org/10.1086/146087
- 12. Cowling, T.G. (1981) The Present Status of Dynamo Theory. Annual Review of Astronomy and Astrophysics, 19, 115- 135. http://dx.doi.org/10.1146/annurev.aa.19.090181.000555
- 13. Larmor, J. (1919) Brit Assoc. Reports, 159.
- 14. Cowling, T.G. (1934) Monthly Notices. Royal Astronomical Society, 94, 39-48. http://dx.doi.org/10.1093/mnras/94.1.39
- 15. Goldstein, H. (1959) Classical Mechanics. Addison-Wesley Publishing, Inc. U.S.A., London.
- 16. Landau, L.D. and Lifshitz, E.M. (1962) The Classical Theory of Fields. Pergamon Press, Addison-Wesley Publishing, Inc., London, Paris.
Appendix
Let us consider any point at the surface of the Outer Core. The strength of the dipole field can be obtained from equation (19) and using the following data [2]
Consequently, the corresponding magnetic induction is
Now, the value of CV con be calculated from (9), to take advantage of the last result and the next data
to obtain that

In order to estimate the strength of the magnetic induction at the Earth’s Equator, the magnitude of Bc in the Crust can be calculated; where the corresponding data has the following values, and using again equation (9), i.e.
Then, in the Crust and near the Earth’s surface one obtains that

The strength of magnetic induction on the Earth’s surface and at the Equator is equal to 0.307 gauss [2] . As it can be easily seen, the theoretical calculation and the direct measurement are practically equal.
Finally, it is important to mention what follows: Concerning the elaboration of an alternative theoretical scheme on the origin and structure of the Geomagnetic field, many researchers have engaged themselves, to the self- exited dynamo models [11] . Unfortunately, the results obtained by them are far from satisfactory even now [12] . The model was initially proposed in 1919 by J. Larmor [13] with the purpose of giving an explanation to the phenomenon of Sunspots. That suggestion was quickly rejected for being inadequate and inconsistent to the astronomical observations about the phenomenon [14] .
However, the model was used, throughout 40 or more years, in order to try giving an explanation of the origin and structure of the magnetic field self-generated by gaseous stars [11] .
Also, by means of this model, the idea is to explain the origin and structure of the magnetic field self-gener- ated by the Earth. In this case it has not been possible to give any satisfactory explanation concerning the basic characteristics of the geomagnetic field either [2] .





