Journal of Geoscience and Environment Protection
Vol.03 No.03(2015), Article ID:56210,16 pages
10.4236/gep.2015.33004
Modeling 3D Ex-Filtration Process of a Soak-Away Rain Garden
Sivarajah Mylevaganam*, Ting Fong May Chui, Jiangyong Hu
Department of Civil and Environmental Engineering, National University of Singapore, Singapore, Singapore
Email: *sivaloga@hushmail.com
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 5 March 2015; accepted 1 May 2015; published 11 May 2015
ABSTRACT
This paper presents a three-dimensional (3D) model developed using COMSOL Multiphysics to understand the 3D ex-filtration process of a soak-away rain garden. With a design hyetograph of 3-month average rainfall intensities of Singapore, it is found that the average vertical ex-filtration rate that is obtained by dividing the average vertical ex-filtration (drained through bottom of the soak-away rain garden, averaged over the simulation period = 720 min, and expressed in m3) by the surface area of the soak-away rain garden and the simulation time step is almost constant regardless of increase in saturated hydraulic conductivity (K) of the in-situ soil and the surface area of the soak-away rain garden as a percentage of catchment area. However, as depth to groundwater table which is measured from bottom of the filter media increases, in between 0.5 m and 1 m of depth to groundwater table, the average vertical ex-filtration rate decreases significantly (by around 15 - 20 mm/hr) and the decrease is almost twice, compared with that between 1 m and 1.5 m of depth to groundwater table. Furthermore, this study shows that for a given K of in-situ, K of filter media, and depth to groundwater table, as the surface area of the soak-away rain garden increases, the horizontal flow coefficient which is defined as the ratio between total horizontal ex-filtration (drained through sides of the soak-away rain garden, summed over the simulation period, and expressed in m3) and total vertical ex-filtration (drained through bottom of the soak-away rain garden, summed over the simulation period, and expressed in m3) decreases. Moreover, for a given surface area of the soak-away rain garden, K of in-situ, and depth to groundwater table, the horizontal flow coefficient decreases as K of the filter media increases. However, it is found that for a given surface area of the soak-away rain garden, K of in-situ, and K of filter media, the horizontal flow coefficient increases as depth to groundwater table increases.
Keywords:
COMSOL Multiphysics, 3D Ex-Filtration, Soak-Away Rain Garden, Average Vertical Ex-Filtration Rate, Horizontal Flow Coefficient

1. Introduction
To mitigate the adverse impact of urbanization around the world, several best management practices, in other words, green infrastructures, have been used in a way that protect the natural hydrology of the catchment and are more beneficial to the environment [1] -[5] . Soak-away rain garden, shallow, landscaped depressions commonly located in parking lots or within small pockets in residential areas, is one of those best management practices or green infrastructures. Despite the rapid acceptance of soak-away rain gardens throughout the world by water managers and land-use planners, fundamental understandings of these green infrastructures are still at undeveloped stage [1] [2] . Detailed hydrologic performance information and related hydrologic design guidelines of soak-away rain gardens are not currently available for many regions including Singapore. Thus, assuming performance to be independent of many highly dynamic conditions to which these facilities expose [1] , water managers often adopt existing published hydrologic design guidelines, which are often represented as relationships such as a relationship between the overflow volume and surface area (as a % of catchment area) of the soak- away rain garden or the saturated hydraulic conductivity of the in-situ soil, without modifying the guidelines for local conditions. Therefore, to assist local water managers, these relationships that are specific for local conditions need to be established. To establish such relationships using any stormwater models that also have water quality components, such as MUSIC (model for urban stormwater improvement conceptualization), it is equally important to study the ex-filtration or draining of water into the surrounding soils, which helps in reducing the stormwater volume, of the soak-away rain garden and its relationship with the saturated hydraulic conductivity of the in-situ soil, the saturated hydraulic conductivity of the filter media (the primary soil layer), size of the soak-away rain garden, etc. However, as underscored in the literature [1] [2] , there is a lack of studies that focus on understanding the ex-filtration process of a soak-away rain garden. On the other hand, the ex-filtration process of a soak-away rain garden may differ significantly in horizontal and vertical directions, as it depends on many factors [1] - [5] . Therefore, there exists a need to study the three-dimensional (3D) ex-filtration process of a soak- away rain garden. Having said this, it may not be feasible to study the 3D ex-filtration process of a soak-away rain garden in a sufficient level of details in an experimental setup, specifically in the field. Moreover, though in the past few decades the mathematical modeling work and the science of computer simulation have enhanced the understanding of hydrological processes, there is still a lack of modeling studies that focus on exploring the 3D ex-filtration process of a soak-away rain garden in a sufficient level of details [2] . Therefore, to understand and get the preliminary view on the 3D ex-filtration process of a soak-away rain garden in a sufficient level of details, a comprehensive mathematical modeling work is required, which is independent of field data. Thus, it is the objective of this study to explore the 3D ex-filtration process of a soak-away rain garden, specifically the average vertical ex-filtration rate and the horizontal flow coefficient, by developing a 3D mathematical model based on Richard’s equation [6] -[8] using COMSOL Multiphysics [7] [8] .
2. COMSOL Multiphysics
COMSOL Multiphysics is a powerful interactive environment for modeling and solving partial differential equations in scientific and engineering problems. The software provides a powerful integrated desktop environment with a Model Builder where the users get full overview of the model and access to all functionality. With COMSOL Multiphysics the users can easily extend models for one type of physics into multiphysics models that solve coupled physics phenomena. COMSOL Multiphysics also allows the users to perform various types of studies such as stationary and time-dependent studies. When solving the models, COMSOL Multiphysics uses the proven finite element method. The software runs the finite element analysis together with adaptive meshing and error control using a variety of numerical solvers. A more detailed description of the mathematical and numerical foundation is in the COMSOL Multiphysics Reference Guide [8] .
3. Methodology and Discussion of Results
This section of the paper is divided into three sub-sections. Sub-section 3.1 describes the 3D model development in COMSOL Multiphysics, Sub-section 3.2 briefly summarizes the hyetograph to represent the 3-month average rainfall intensities (ARIs), which was used to simulate the developed model, and Sub-section 3.3 discusses the results.
3.1. Model Development in COMSOL Multiphysics
Modeling of a soak-away rain garden involves flow in variably saturated porous media. Flow in variably saturated porous media is modeled using the Earth Sciences Module (Subsurface Flow Module) of COMSOL Multiphysics. A review of COMSOL’s Earth Sciences Module for simulating flow in variably saturated porous media can be found in [9] . Using the Earth Sciences Module of COMSOL, to develop a model in variably saturated porous media, among other things, it is required to define the model geometry, the mathematical representation of the physical processes of interest, the initial/boundary conditions, and the water balance of the soak-away rain garden.
3.1.1. Model Geometry Using COMSOL Multiphysics
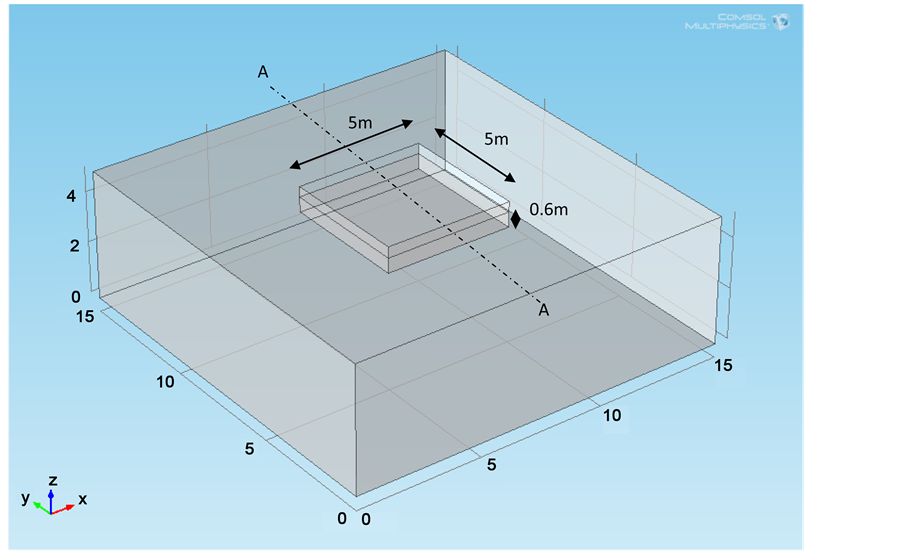
Figure 1 shows the 3D geometry of a soak-away rain garden that allows stormwater runoff to ex-filtrate into the surrounding soil. For demonstration purpose, a soak-away rain garden with a width of 5 m and a height of 1.0 m is chosen. The length of the soak-away rain garden is 5 m. The shape of the soak-away rain garden is assumed to be of rectangular/square shape. The height of the filter media, the primary soil layer, is 0.6 m. The height of the ponding space, which is defined above the filter media, is limited to 0.2 m. The width and length of the area of the influence is 15 m.
Using COMSOL Multiphysics, the 3D geometry of the soak-away rain garden of the above mentioned dimensions was formed by first creating a block feature, whose block name is “blk1”, to represent the outer dimensions. The width and the length of this block were set to “15” and the height was set to “5”. Similar to block feature, “blk1”, another block feature, whose block name is “blk2”, was created. The width and the length of this block were set to “5” and the height was set to “1”, but the block position was set to (5, 5, 4) in (X, Y, Z) direction. To represent the in-situ soil, the block feature, “blk2”, was subtracted from the block feature, “blk1”, by creating a Difference feature (“dif1”), a Boolean operation with the 'input' properties set to “blk1” and “blk2”. To represent the filter media, similar to block features “blk1” and “blk2”, another block feature, whose block name is “blk3”, was created. The width and the length of this block were set to “5” and the height was set to “0.6”, but the block position was set to (5, 5, 4) in (X, Y, Z) direction. To represent the soak-away rain garden, the block feature “blk3” was unioned with the Difference feature (“dif1”), by creating a Union feature (“uni1”), a Boolean operation with the 'input' properties set to “blk3” and “diff1”.
Figure 1. Graphical representation of a soak-away rain garden in COMSOL Multiphysics.
3.1.2. Representation of the Physical Processes Using COMSOL Multiphysics
Richards’ equation models flow in variably saturated porous media. Many efforts to simplify and improve the modeling of flow in variably saturated media have produced a number of variants of Richards’ equation. In this paper, the form of the Richards’ equation adopted in COMSOL Multiphysics is used [7] [8] . The Richards’ equation was applied for both the in-situ soil and the filter media of the soak-away rain garden. The adopted equation is presented in Equation (1).
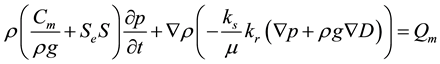 (1)
(1)
where the pressure, p, is the dependent variable. In this equation, Cm represents the specific moisture capacity, Se denotes the effective saturation, S is the storage coefficient, κs gives the hydraulic permeability, μ is the fluid dynamic viscosity, kr denotes the relative permeability, ρ is the fluid density, g is acceleration of gravity, D represents the elevation, and Qm is the fluid source (positive) or sink (negative). The fluid velocity across the faces of an infinitesimally small surface is given by Equation (2).
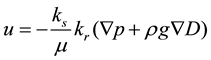 (2)
(2)
where u is the flux vector. The porous medium consists of pore space, fluids, and solids, but only the liquids move. Equation (2) describes the flux as distributed across a representative surface. To characterize the fluid velocity in the pores, COMSOL Multiphysics also divides u by the volume liquid fraction, θs. This interstitial, pore or average linear velocity is ua = u/θs [7] [8] .
3.1.3. Initial/Boundary Conditions Using COMSOL Multiphysics
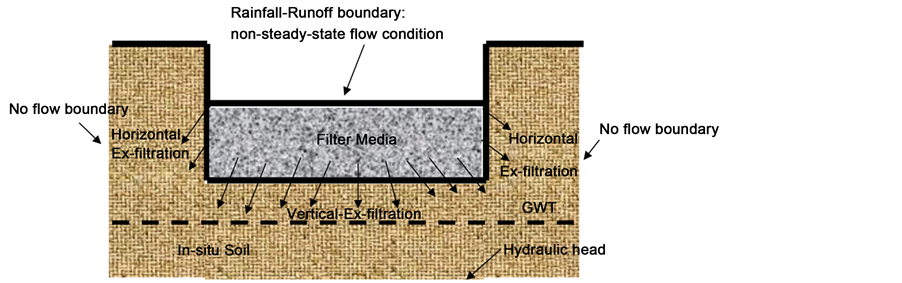
To solve flow in variably saturated porous media, it is necessary that appropriate boundary conditions are specified. From a mathematical standpoint, the application of boundary conditions ensures that the solutions to the problems are self-consistent. In this study, the following boundary conditions are identified as appropriate. As shown in Figure 2, which represents the frontal view of cut-plane (YZ Plane) A-A of Figure 1, the top surface of the rain garden is a rainfall-runoff boundary, a non-steady-state flow condition typical of urban stormwater runoff. The external side boundaries do not allow water to flow in or out of the area of influence, implying that the chosen area is large enough that it does not affect the flow performance around the rain garden. The bottom boundary of the area of influence is specified by a hydraulic head corresponding to an assumed groundwater table level. When water starts to pond, the boundary condition at the top surface of the rain garden becomes a hydraulic boundary. Therefore, there is a need to be able to switch the top surface of the rain garden from flow to hydraulic head. The switching was done using COMSOL Java API, a Java-based interface [7] [8] . The initial condition was set to hydrostatic condition. In other words, above groundwater table, the suction is equal to the distance above groundwater table.
3.1.4. Water Balance of the Soak-away Rain Garden Using COMSOL Multiphysics
Water Balance of the soak-away rain garden was carried out using a continuity equation whose components are stormwater runoff, overflow (which is the excess of the ponding space), change of soil moisture within the filter media, change of water storage within the ponding space, vertical ex-filtration, and horizontal ex-filtration. At a given time, horizontal ex-filtration and vertical ex-filtration were computed by integrating the model computed velocity along the four side walls and the bottom surface of the soak-away rain garden, respectively.
3.2. Development of Design Hyetograph
The design of soak-away rain gardens involves water quality. Thus, the establishment of a design hyetograph for the design of soak-away rain gardens, specifically, requires data on intensity-duration-frequency (IDF) values for relatively frequent storms such as 3-month ARIs that carry up to 90% of the total load on annual basis. As underscored in the literature, to date, there are few methods available for the establishment of design hyetographs using IDF data [10] . In this paper, the alternating block method [10] , which represents an event of a selected return period both for the selected duration of the event and for any period within this selected duration, is used in developing a design hyetograph from an IDF relationship of Singapore. A storm duration of 720 min
Figure 2. Boundary conditions of a soak-away rain garden in COMSOL Multiphysics.
was considered. Considering an event of 720 min of the 3-month ARIs, a design hyetograph for 3-month ARIs built-up using this method represents a 3-month ARI event both for the 720 min total duration and for any period (i.e., 5 min, 10 min, 15 min, 30 min, 60 min,…, 360 min) within this duration centered on the maximum block [10] . The design hyetograph produced by this method specifies the rainfall depth occurring in n successive time intervals of duration Δt over a total duration of 720 min = nΔt. Duration Δt is often determined by the finest resolution of the hydrological model that is used to generate the design hydrograph, the time distribution of discharge. The hyetograph to represent a 3-month ARI event of 720 min duration is shown in Figure 3 for a duration (Δt) of 6 min which is the finest resolution of MUSIC (Model for urban stormwater improvement conceptualization) model which was used to generate the hydrographs for different urbanized (impervious percentage of 90% was assumed) catchment sizes varied from 100 to 250 m2.
3.3. Discussion of Results
In this study, as shown in Figure 4, the simulation was carried out for different values of in-situ hydraulic conductivity, surface area of the soak-away rain garden (as % of catchment area), saturated hydraulic conductivity of the filter media, and depth to groundwater table measured from bottom of the filter media. The in-situ hydraulic conductivity was varied from 10 mm/hr to 50 mm/hr, typical range in Singapore. The surface area of the soak-away rain garden (as a % of catchment area) was varied from 6% to 15%. The width and the length of the soak-away rain garden were assumed to be of the same size. The saturated hydraulic conductivity of the filter media was varied from 100 mm/hr to 200 mm/hr, typical range in Singapore. The depth to groundwater table was varied from 0.5 m to 1.5 m.
3.3.1. Variation of Average Vertical Ex-Filtration
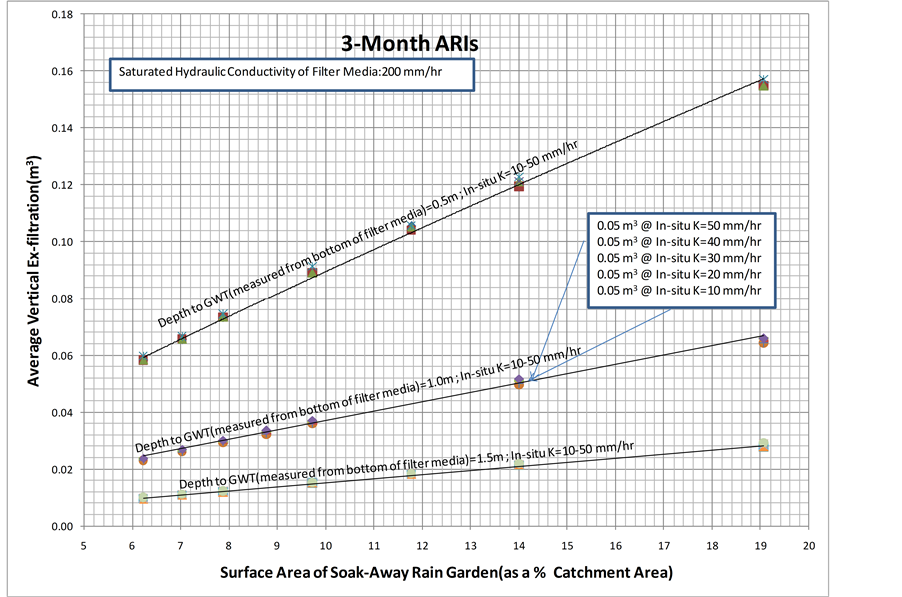
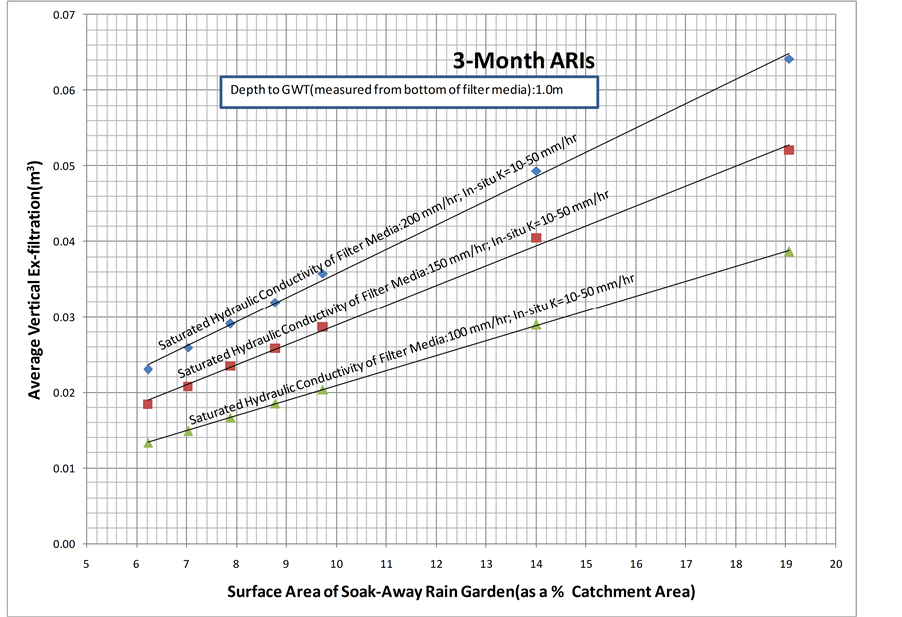
Figure 5 shows the graph of average vertical ex-filtration (drained through bottom of the soak-away rain garden, averaged over the simulation period = 720 min, and expressed in m3) versus the surface area of the soak-away rain garden (as a % of catchment area). For this graph, the saturated hydraulic conductivity of the filter media was set to 200 mm/hr and the depth to groundwater table measured from bottom of the filter media was varied from 0.5 m to 1.5 m. The graph also shows the variation with the saturated hydraulic conductivity of the in-situ soil. As can be observed from the graph, for the considered saturated hydraulic conductivity of the filter media, depths to groundwater table, and saturated hydraulic conductivities of the in-situ soil, the average vertical ex- filtration increases as the surface area of the soak-away rain garden increases. This is owing to the fact that the ex-filtrated water, which is drained through bottom of the soak-away rain garden, is proportional to bottom surface area of the soak-away rain garden.
Furthermore, it is also noted that as depth to groundwater table increases the average vertical ex-filtration decreases. This could be due to the fact that the ex-filtrated flow is inversely proportional to the flow length. Moreover, for a given surface area of the soak-away rain garden (as a % of catchment area) and depth to groundwater table, the average vertical ex-filtration is not influenced significantly as the saturated hydraulic conductivity of the in-situ soil increases. On the other hand, as shown in Figures 6-8, for the considered surface areas of the soak- away rain garden and depths to groundwater table, the average vertical ex-filtration increases as the saturated hydraulic conductivity of the filter media increases. This is due to the fact that as the saturated hydraulic
Figure 3. Design hyetograph for 3-month ARIs.
Figure 4. Simulated ranges of saturated hydraulic conductivity of the in-situ soil and surface area of the soak-away rain garden for a given depth to ground- water table and saturated hydraulic conductivity of the filter media.
conductivity of the filter media increases, the ability of the soil fluid to flow through the soil matrix system increases too.
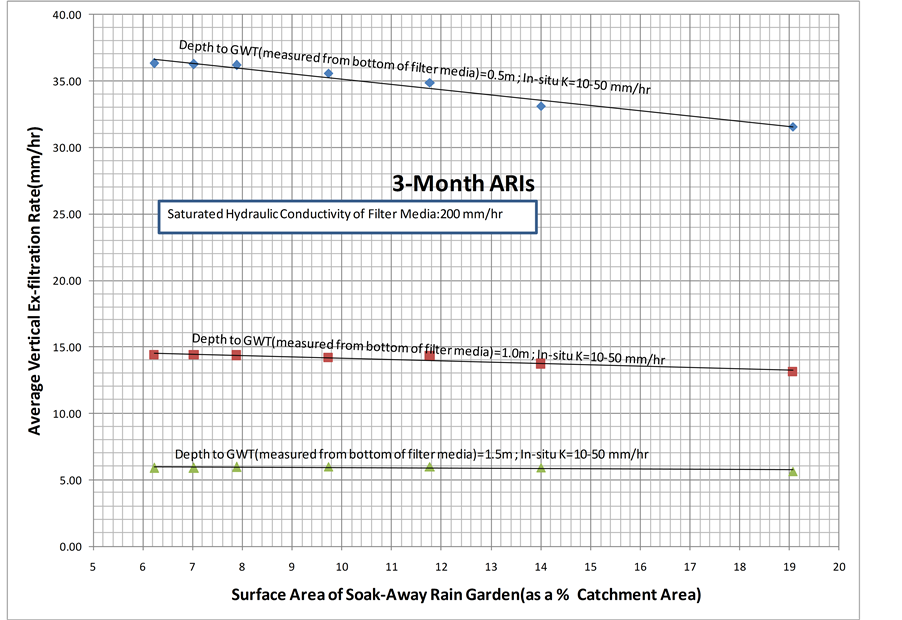
To understand the above discussed behaviors in more detail, a graph of average vertical ex-filtration rate, which is obtained by dividing the average vertical ex-filtration by the surface area of the soak-away rain garden and the simulation time step, versus the surface area of the soak-away rain garden (as a % of catchment area) was plotted. As shown in Figure 9, the saturated hydraulic conductivity of the filter media was set to 200 mm/hr, saturated hydraulic conductivity of the in-situ soil was varied from 10 mm/hr to 50 mm/hr, and the depth to groundwater table measured from bottom of the filter media was varied from 0.5 m to 1.5 m.
As can be observed from the graph, for the considered saturated hydraulic conductivities of the in-situ soil
Figure 5. The average vertical ex-filtration for a saturated hydraulic conductivity of the filter media of 200 mm/hr.
Figure 6. The average vertical ex-filtration for a depth to groundwater table of 0.5 m.
Figure 7. The average vertical ex-filtration for a depth to groundwater table of 1.0 m.
Figure 8. The average vertical ex-filtration for a depth to groundwater table of 1.5 m.
Figure 9. The average vertical ex-filtration rate for a saturated hydraulic conductivity of the filter media of 200 mm/hr.
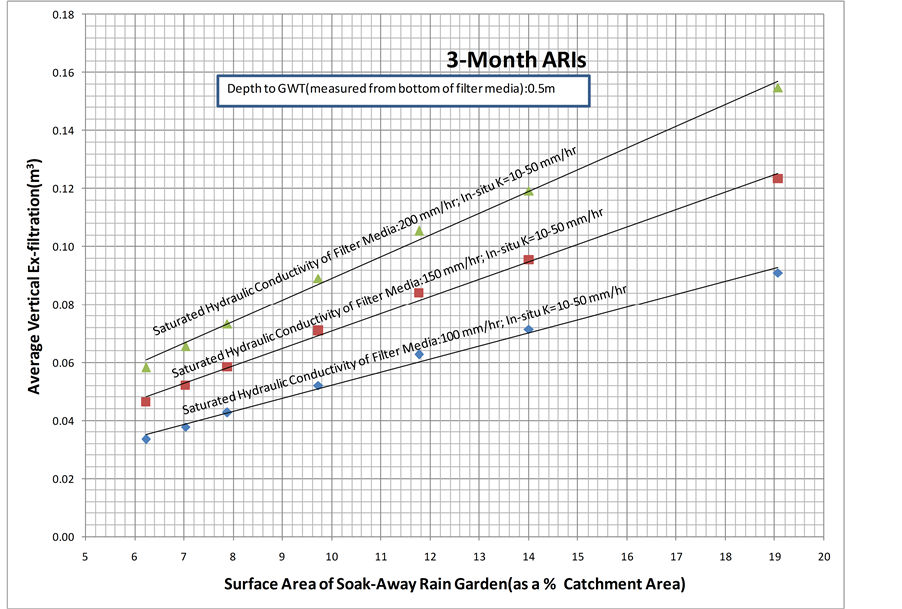
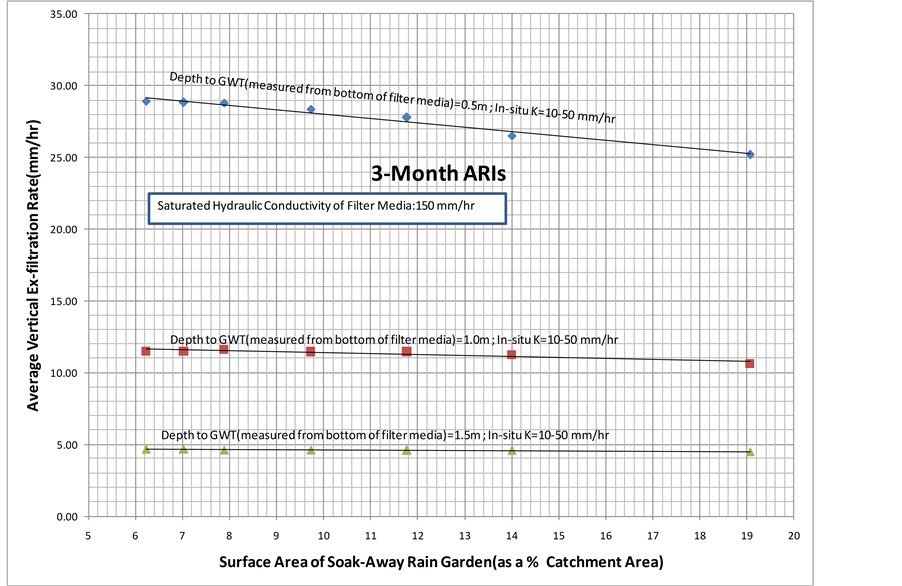
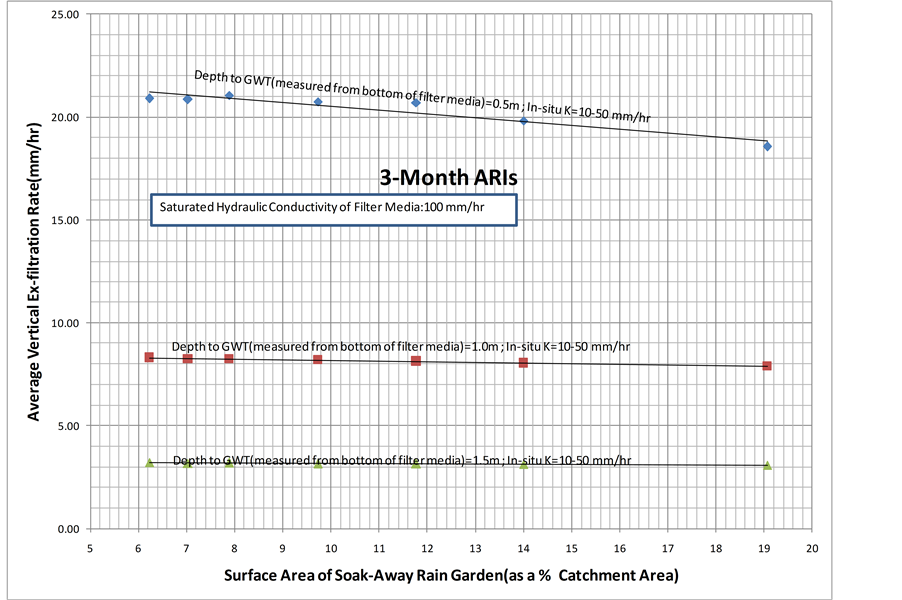
and for a given depth to groundwater table, the average vertical ex-filtration rate is nearly constant regardless of increase in the surface area of the soak-away rain garden (as a % of catchment area). This indicates that although the average vertical ex-filtrated water through bottom surface of the soak-away rain garden increases as surface area of the soak-away rain garden (as a % of catchment area) increases, the average vertical ex-filtration rate is nearly constant. This could be due to the reason that the incremental/fractional increase on average vertical ex- filtration is approximately equal to the incremental/ fractional increase on surface area of the soak-away rain garden. Furthermore, as shown in Figure 10 and Figure 11, the above discussed behaviors are also observed when the saturated hydraulic conductivity of the filter media is 150 mm/hr and 100 mm/hr.
As previously, it is also noted that as depth to groundwater table increases the average vertical ex-filtration rate decreases. However, as the depth to groundwater table increases, in between 0.5 m and 1 m of depth to groundwater table, the average vertical ex-filtration rate decreases significantly (by around 15 - 20 mm/hr) and the decrease is almost twice, compared with that between 1 m and 1.5 m of depth to groundwater table.
3.3.2. Variation of Horizontal Flow Coefficient
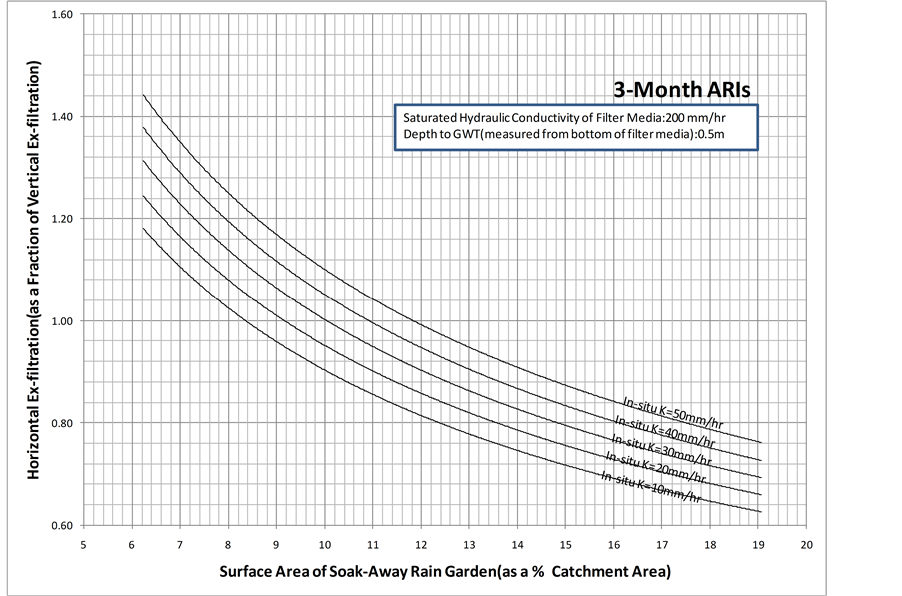
To understand the variation of horizontal ex-filtration, as shown in Figure 12, the graph of horizontal flow coefficient which is defined as the ratio between total horizontal ex-filtration (drained through sides of the soak- away rain garden, summed over the simulation period = 720 min, and expressed in m3) and total vertical ex-fil- tration (drained through bottom of the soak-away rain garden, summed over the simulation period, and expressed in m3) versus the surface area of the soak-away rain garden (as a % of catchment area) was plotted. For this graph, the saturated hydraulic conductivity of the filter media was set to 200 mm/hr and the depth to groundwater table measured from bottom of the filter media was set to 0.5 m. The graph also shows the variation with saturated hydraulic conductivity of the in-situ soil.
As can be observed from the graph, for the considered saturated hydraulic conductivities of the in-situ soil, as surface area of the soak-away rain garden (as a % of catchment area) increases, the horizontal flow coefficient decreases. The possible reason for this observation is that as surface area of the soak-away rain garden increases,
Figure 10. The average vertical ex-filtration rate for a saturated hydraulic conductivity of the filter media of 150 mm/hr.
Figure 11. The average vertical ex-filtration rate for a saturated hydraulic conductivity of the filter media of 100 mm/hr.
Figure 12. Horizontal flow coefficient for a depth to groundwater table of 0.5 m and a saturated hydraulic conductivity of the filter media of 200 mm/hr.
it is expected to have more ex-filtrated water. In other words, it is expected that more vertical and horizontal ex- filtration to occur as surface area of the soak-way rain garden increases. However, as surface area of the soak- away rain garden increases, the increase in total vertical ex-filtration is generally higher than the increase in total horizontal ex-filtration. This is owing to the fact that as surface area of the soak-away rain garden increases, the increase in the base area is generally higher than the increase in the area in the side walls. This can be further explained by considering the simulated results of total horizontal ex-filtration and total vertical ex-filtration for a given in-situ hydraulic conductivity and for two different surface areas of the soak-away rain garden (say 4 m * 4 m and 5 m * 5 m). The total horizontal ex-filtration is 1.00E+01 m3 and 1.21E+01 m3 when the surface area of the soak-away rain garden is 4 m * 4 m and 5 m * 5 m, respectively. On the other hand, the total vertical ex- filtration is 6.98E+00 m3 and 1.07E+01 m3 when the surface area of the soak-away rain garden is 4 m * 4 m and 5 m * 5 m, respectively. Thus, the increase in total vertical ex-filtration is 1.53E+00 (1.07E+01/6.98E+00) whe- reas the increase in total horizontal ex-filtration is 1.21E+00 (1.21E+01/1.00E+01). This confirms that as surface area of the soak-away rain garden (as a % of catchment area) increases, the increase in total vertical ex-filtration is generally higher than the increase in total horizontal ex-filtration, and thus has made the horizontal flow coefficient to decrease. Further to this, the declining trend of Figure 12 also reveals that although it is expected that more vertical and horizontal ex-filtration to occur as surface area of the soak-away rain garden (as a % of catchment area) increases, there exists a surface area of the soak-away rain garden (as a % of catchment area) beyond which the total horizontal ex-filtration becomes lesser than the total vertical ex-filtration.
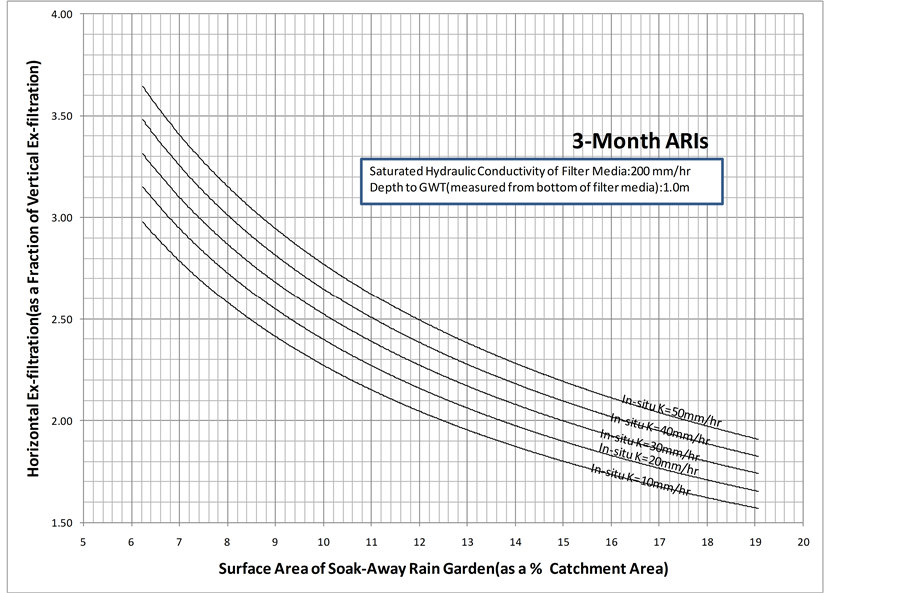
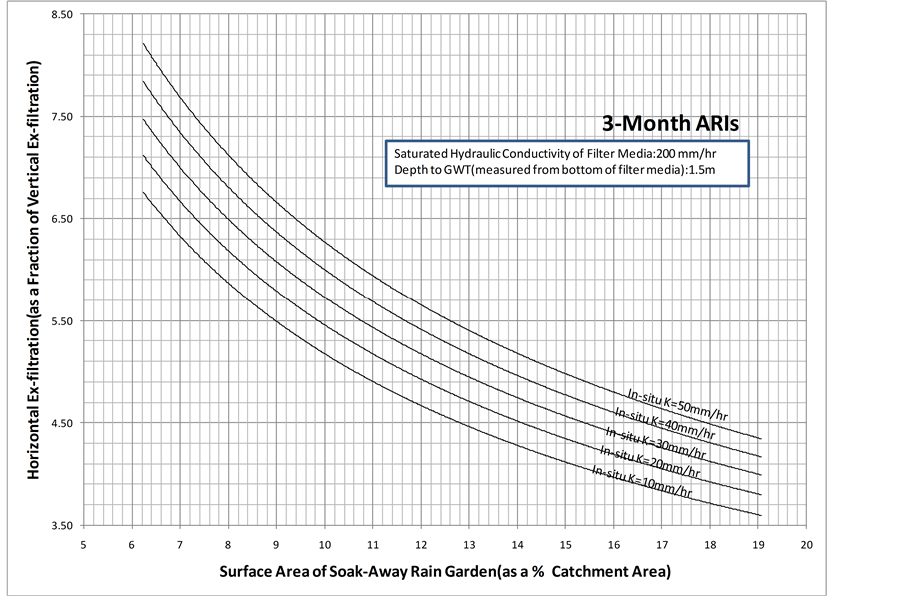
Furthermore, for a given surface area of the soak-away rain garden (as a % of catchment area), the horizontal flow coefficient decreases as the saturated hydraulic conductivity of the in-situ soil decreases. The reason for this observation is that as the saturated hydraulic conductivity of the in-situ soil decreases, it is expected that the quantity of ex-filtrated water coming through vertically and horizontally to decrease. However, the amount of decrease for total horizontal ex-filtration is higher compared to the amount of decrease, which is negligible, for total vertical ex-filtration. As shown in Figure 13 and Figure 14, the above discussed behaviors are also observed when the groundwater table is 1.0 m and 1.5 m below the bottom of the filter media. However, based on Figures 12-14, it is observed that for a given surface area of the soak-away rain garden (as a % of catchment
Figure 13. Horizontal flow coefficient for a depth to groundwater table of 1.0 m and a saturated hydraulic conductivity of the filter media of 200 mm/hr.
Figure 14. Horizontal flow coefficient for a depth to groundwater table of 1.5 m and a saturated hydraulic conductivity of the filter media of 200 mm/hr.
area) and a given saturated hydraulic conductivity of the in-situ soil, as depth to groundwater table increases the horizontal flow coefficient increases. The possible reason for this observation is that as depth to groundwater table goes further down from bottom of the filter media, the flow length increases. However, the flow length is inversely proportional to flow, and thus the total vertical ex-filtration is reduced. Having said this, the total horizontal ex-filtration may not have been influenced by the groundwater table location and has caused the horizontal flow coefficient to increase as the depth to groundwater table increases for a given surface area of the soak-away rain garden and a given saturated hydraulic conductivity of the in-situ soil.
The graphs to represent the saturated hydraulic conductivities of the filter media of 150 mm/hr and 100 mm/hr are placed in Figure 15.
As can be observed from the graphs, for a given surface area of the soak-away rain garden (as a % of catchment area), saturated hydraulic conductivity of the in-situ soil, and depth to groundwater table, the horizontal flow coefficient decreases as the saturated hydraulic conductivity of the filter media increases. The reason for this observation is that as the saturated hydraulic conductivity of the filter media increases, it is expected that the quantity of ex-filtrated water coming through vertically and horizontally to increase. However, the amount of increase for total vertical ex-filtration is higher compared to the amount of increase for total horizontal ex-filtra- tion. The possible reason is that the available area in the side walls for horizontal ex-filtration is lesser than what is available for vertical ex-filtration through the base area of the soak-away rain garden.
4. Conclusions
This paper presents a 3D model developed using COMSOL Multiphysics to understand the 3D ex-filtration process, which plays major roles in reducing stormwater volume, of a soak-away rain garden, shallow, land- scaped depressions commonly located in parking lots or within small pockets in residential areas. With a design hyetograph of 3-month average rainfall intensities of Singapore, the outcome of this study, among other things, shows the followings:
1) The average vertical ex-filtration rate which is obtained by dividing the average vertical ex-filtration (drained through bottom of the soak-away rain garden, averaged over the simulation period = 720 min, and expressed in m3) by the surface area of the soak-away rain garden and the simulation time step is almost constant regardless of increase in saturated hydraulic conductivity of the in-situ soil and the surface area of the soak-away rain garden as a % of catchment area. However, as depth to groundwater table measured from bottom of the filter media increases, in between 0.5 m and 1 m of depth to groundwater table, the average vertical ex-filtration rate decreases significantly (by 15 - 20 mm/hr) and the decrease is almost twice, compared with that between 1 m and 1.5 m of depth to groundwater table.
2) For a given saturated hydraulic conductivity of the in-situ soil, saturated hydraulic conductivity of the filter media, and depth to groundwater table, as surface area of the soak-away rain garden as a % of catchment area increases, the horizontal flow coefficient which is defined as the ratio between total horizontal ex-filtration (drained through sides of the soak-away rain garden, summed over the simulation period = 720 min, and expressed in m3) and total vertical ex-filtration (drained through bottom of the soak-away rain garden, summed over the simulation period, and expressed in m3) decreases. In other words, as surface area of the soak-away rain garden (as a % of catchment area) increases, the fractional/proportional increase in total vertical ex-filtration is higher than the fractional/proportional increase in total horizontal ex-filtration. Similarly, for a given surface area of the soak- away rain garden, saturated hydraulic conductivity of the in-situ soil, and depth to groundwater table, the horizontal flow coefficient decreases as the saturated hydraulic conductivity of the filter media increases. However, it is found that for a given surface area of the soak-away rain garden, saturated hydraulic conductivity of the in- situ soil, and saturated hydraulic conductivity of the filter media, the horizontal flow coefficient increases as depth to groundwater table increases.
3) Although it is expected that more total vertical and total horizontal ex-filtration to occur as surface area of the soak-away rain garden (as a % of catchment area) increases, there exists a surface area of the soak-away rain garden (as a % of catchment area), beyond which the total horizontal ex-filtration becomes less than the total vertical ex-filtration.
Acknowledgements
The authors would like to thank PUB, Singapore’s national water agency, for providing the financial support to
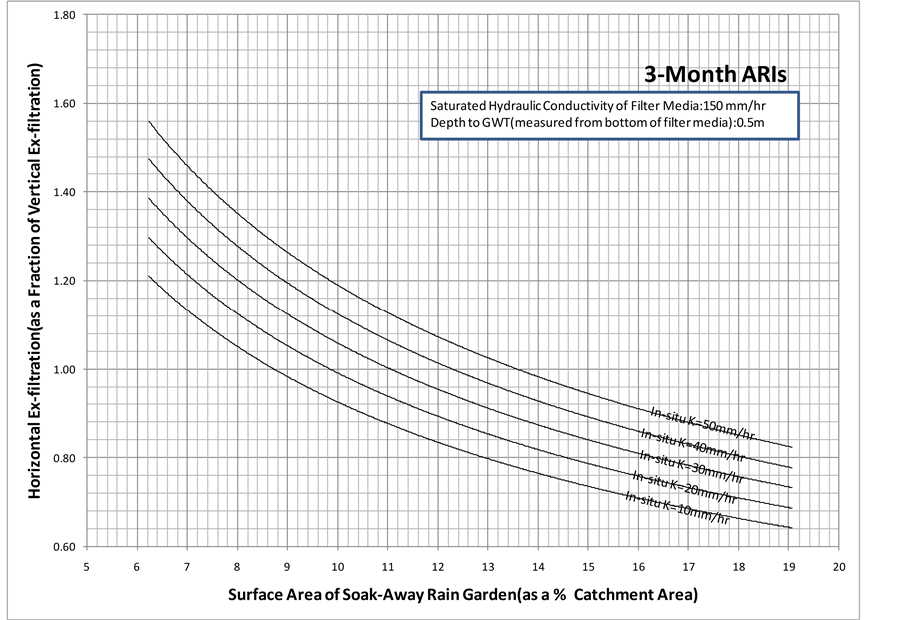
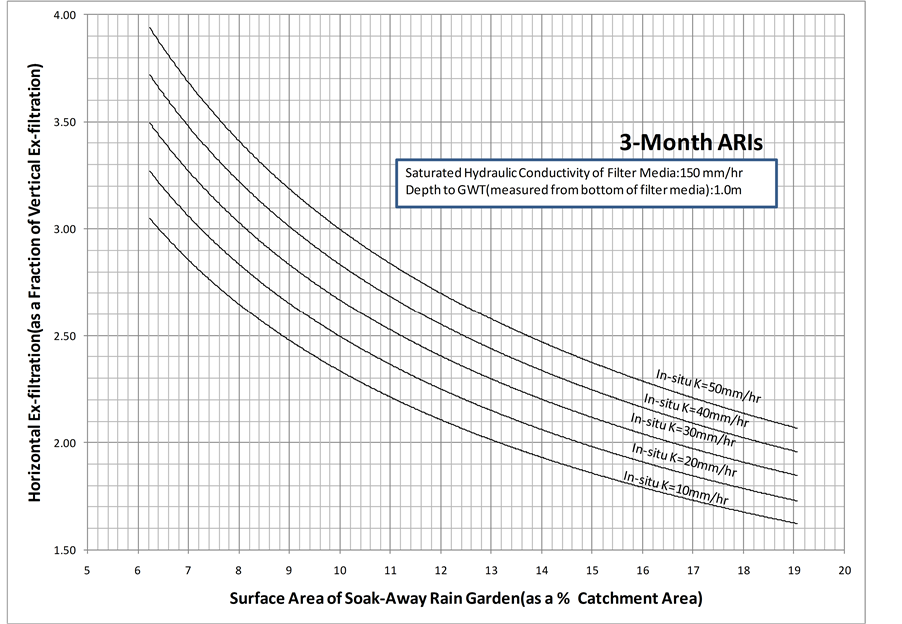
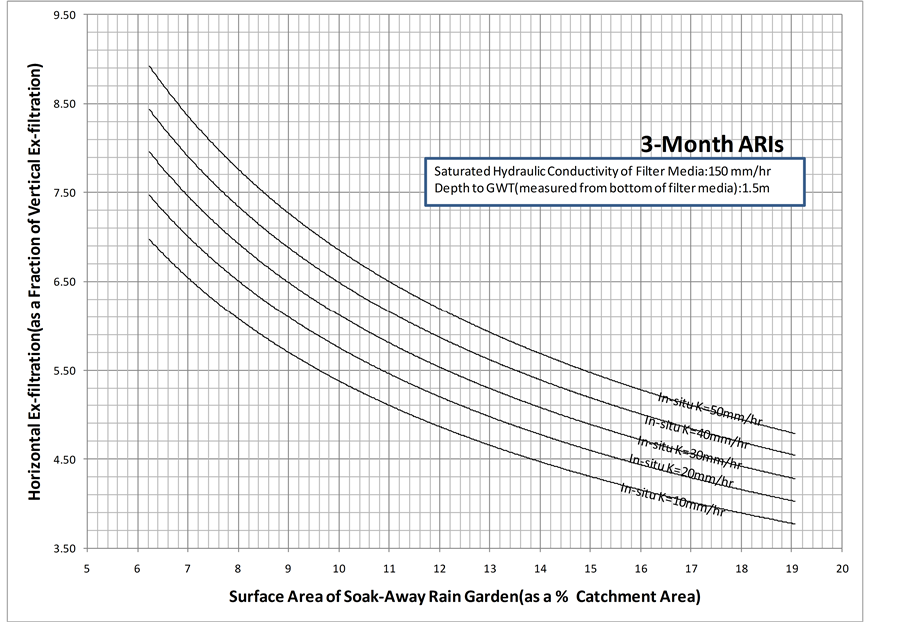
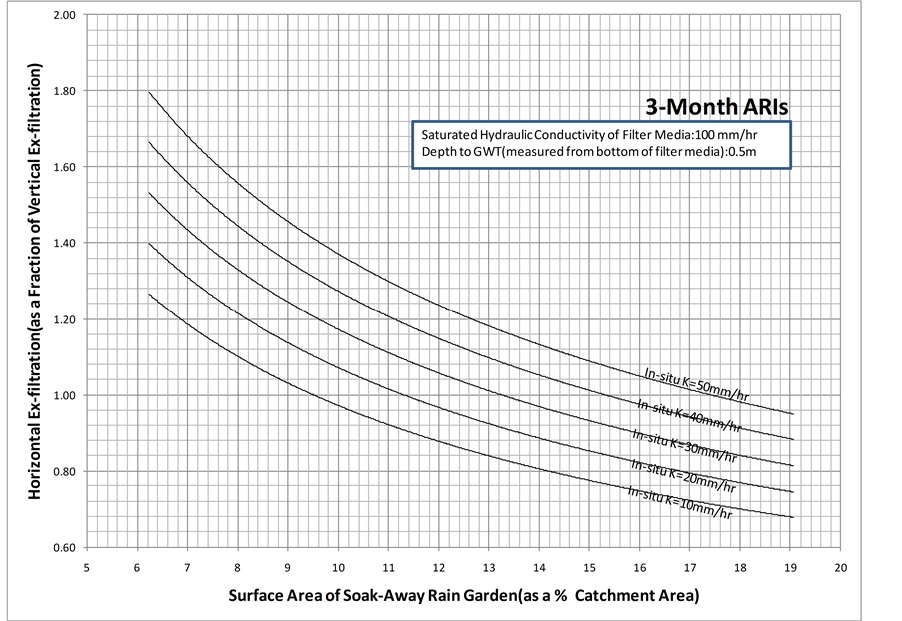
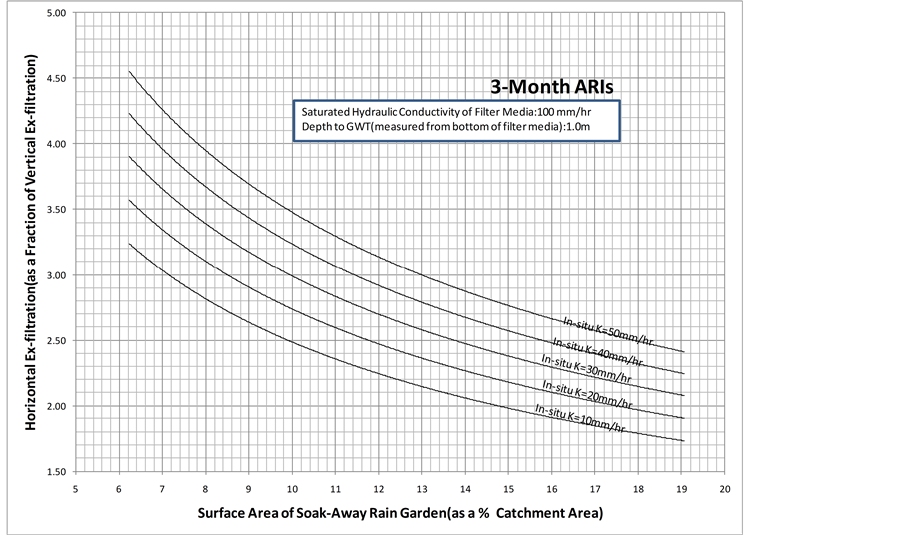
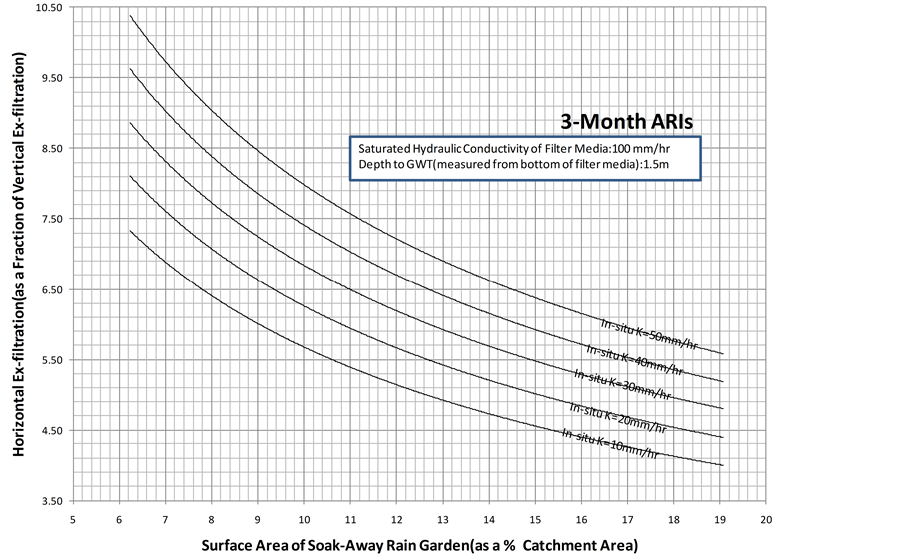
Figure 15. Horizontal flow coefficient for a (a) Depth to groundwater table of 0.5 m and a saturated hydraulic conductivity of the filter media of 150 mm/hr; (b) Depth to groundwater table of 1.0 m and a saturated hydraulic conductivity of the filter media of 150 mm/hr; (c) Depth to groundwater table of 1.5 m and a saturated hydraulic conductivity of the filter media of 150 mm/hr; (d) Depth to groundwater table of 0.5 m and a saturated hydraulic conductivity of the filter media of 100 mm/hr; (e) Depth to groundwater table of 1.0 m and a saturated hydraulic conductivity of the filter media of 100 mm/hr; (f) Depth to groundwater table of 1.5 m and a saturated hydraulic conductivity of the filter media of 100 mm/hr.
conduct this research. The first author, who was a researcher at National University of Singapore, is currently attached to South Eastern University of Sri Lanka.
References
- Allan, P.D., Robert, G.T. and William, F.H. (2010) Improving Urban Stormwater Quality: Applying Fundamental Principles. Journal of Contemporary Water Research and Education, 146, 3-10. http://dx.doi.org/10.1111/j.1936-704X.2010.00387.x
- Jia, L., David, J.S., Cameron, B. and Yuntao, G. (2014) Review and Research Needs of Bioretention Used for the Treatment of Urban Stormwater. Water, 6, 1069-1099. http://dx.doi.org/10.3390/w6041069
- Hunt, W.F., Jarrett, A.R., Smith, J.T. and Sharkey, L.J. (2006) Evaluating Bioretention Hydrology and Nutrient Removal at Three Field Sites in North Carolina. Journal of Irrigation and Drainage Engineering, 132, 600-608. http://dx.doi.org/10.1061/(ASCE)0733-9437(2006)132:6(600)
- Jones, M.P. and Hunt, W.F. (2009) Bioretention Impact on Runoff Temperature in Trout Sensitive Waters. ASCE Journal of Environmental Engineering, 135, 577-585. http://dx.doi.org/10.1061/(ASCE)EE.1943-7870.0000022
- Li, H., Sharkey, L.J., Hunt, W.F. and Davis, A.P. (2009) Mitigation of Impervious Surface Hydrology Using Bioretention in North Carolina and Maryland. ASCE Journal of Hydrologic Engineering, 14, 407-415. http://dx.doi.org/10.1061/(ASCE)1084-0699(2009)14:4(407)
- Richards, L.A. (1931) Capillary Conduction of Liquids through Porous Mediums. Journal of Applied Physics, 1, 318- 333. http://dx.doi.org/10.1063/1.1745010
- COMSOL AB (2012) COMSOL Multiphysics User’s Guide (Version 4.3). Stockholm, Sweden.
- COMSOL AB (2012) COMSOL Multiphysics Reference Guide (Version 4.3). Stockholm, Sweden.
- Li, Q., Ito, K., Wu, Z., Lowry, C.S. and Loheide II, S.P. (2009) COMSOL Multiphysics: A Novel Approach to Ground Water Modeling. Groundwater, 47, 480-487. http://dx.doi.org/10.1111/j.1745-6584.2009.00584.x
- Chow, V.T., Maidment, D.R. and Mays, L.W. (1988) Applied Hydrology. McGraw Hill, New York.
NOTES
*Corresponding author.