Journal of Textile Science and Technology
Vol.01 No.02(2015), Article ID:59261,7 pages
10.4236/jtst.2015.12009
Investigation of Electrical Stability of Nonwovens with Conductive Circuits Using Printed Conductive Inks
A. Maarouf1*, M. Chahid1*, M. Ouarch2
1Sciences Faculty Ben M.Sik, Polymer Physics and Critical Phenomena Laboratory, Research Center Materials and Energy, Casablanca, Morocco
2CRMEF, EL Jadida, Morocco
Email: *abdelwahad.maarouf@gmail.com, *Mustapha.chahid@gmail.com
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 14 July 2015; accepted 25 August 2015; published 28 August 2015
ABSTRACT
In this work, we study the stability of a class of materials obtained by printing a textile with conductive inks using a method called screen printing. Under the action of a certain external factors, the printed circuit suffers deterioration and the conductivity decreases considerably. In this work, we propose to model the overall damage of the textile sheet in terms of the partial damages of the conductive lines. We also apply this approach to evaluate the damage of a system being made of transmission lines printed into nonwoven substrates using different conductive inks.
Keywords:
Electroconductive Textiles, Conductive Inks, Nonwovens, Printed Circuit, Damage

1. Introduction
Terms such as “smart textiles” or “intelligent textiles” refer to textiles that are able to sense stimuli from the surrounding environment as well as to react and adapt to them. In this category, one finds electro-textiles (or e-textiles) which are becoming an emerging field in industry. The range of possible applications they can have is very wide and spreads from medicine [1] [2] to telecommunications [3] , and wearable computing [4] . In a world, which is becoming rapidly interconnected by technology, the addition of e-textiles components to everyday products will provide the ability to enhance product performance and provide new services to customers. The challenges, in the wearable e-textiles area, are achieving reliable and robust interconnect formation, improving signal integrity, and maintaining textiles characteristics such as lightweight and flexibility [4] -[7] . An electro conductive sheet being woven or knitted can be treated as a combination of serial and parallel connections of resistors that correspond to the resistivity to the fibers themselves, and the resistance between fibers that are interlaced (contact resistance). These parameters depend on numerous external factors such as humidity, mechanical or thermal stresses such as temperature, pressure or extension [8] -[11] .
In addition, the current flow itself in these resistor networks can lead to deterioration by wear of the fibers, and long-term rupture. Such is the case, for example, of certain sensors synthesized from a conductive polymer composite (CPC), and having piezoelectric properties [12] -[14] . These sensors are used, in fact, for a specific application in the aeronautical field, which consists in measuring the fabric deformations in a parachute canopy manufacture. The study of these materials has shown that the variation of the electrical resistance of these CPC sensors can result from two phenomena [15] . The first one is related to a transformation in the sensor geometry. However, the second one is associated with an intrinsic physico-chemical modification of the sensor material. For the first case, the elongation of the sensor in one direction will cause a shrinking in the other two directions resulting in a decrease in cross-section, and the electrical resistance will increase. In the second case, the intrinsic alteration of the sensor by an external phenomenon may be caused, for example, by a change in the electrical conduction of the conductive particles, or by a modification in the quality of the polymer/filler particle interface [15] . Note that, in our approach, we will limit ourselves to the case where the change in conductivity is mainly due to a geometric change in the resistance section.
In this work, based on the Kachanov damage [16] , the purpose is to propose a model which allows to monitor the damage of printed electric circuits onto nonwoven substrate using different conductive inks for wearable electronic textile applications [17] [18] . The printed nonwoven substrate is exposed to numerous wash cycles to determine the durability properties. The viscosity of the ink dictates the performance of the printed media during washing trials. The inks begin to degrade and display lower conductivity after twenty-five wash cycles [19] . Our approach will allow us, if we know the stage of deterioration of each transmission line, to predict that of the whole system. Moreover, this will lead also to highlight the communicative character of the components damage. Indeed, when a conductive line is damaged (cracked, for example), the transferred current varies, and therefore, other fibers forming the network are affected and their condition of wear will necessarily depend on that of their neighbors. In what follows, we will first start by considering the case of a textile sheet solicited in the longitudinal direction, and in addition, the system is considered to be composed of printed conductive lines in parallel. The transverse case is more complicated, but we consider that the conductive path can be modeled (as a first approximation) by serial connected resistors. We emphasize that the present work is an extension of some previous one that is concerned with the damage of components in correlated systems [20] .
Finally, in the second part of this work, we exploit some experimental results relating to a screen printing process, in which a thick film of polymer is deposited onto nonwoven substrate called Evolon. In fact, in this study, the resistance of each conductive line is measured individually after being subjected to various wash cycles [17] [19] . We applied our damage model to determine experimentally the overall damage, in terms of the partial damages associated to the printed transmission lines. This enabled us to plot the damage curves for different inks and therefore to compare their efficiency.
2. Modeling of the Electrical Damage
The considered textile is a material made of conductive printed lines embedded in an insulating substrate (matrix). The electrical conductivity, in this kind of materials, is not isotropic, and this anisotropy depends essentially on fiber’s orientation, but also on the density of contacts between the adjacent fibers. In the longitudinal case, the electrical conductivity is mainly along the conductive lines, and the associated overall resistor 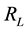 , can be described by considering that the composite is treated as a set of resistors connected in parallel [21] [22] . To determine the resistors damage factor
, can be described by considering that the composite is treated as a set of resistors connected in parallel [21] [22] . To determine the resistors damage factor 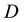 , the starting point is the definition proposed by Kachanov [16] .
, the starting point is the definition proposed by Kachanov [16] .
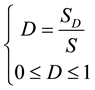 (1)
(1)
Here,  is the area of the damaged surface and
is the area of the damaged surface and 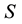 is that of the overall system. This expression suggests that the damage variable
is that of the overall system. This expression suggests that the damage variable 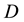 can be regarded as a probability. Furthermore, recall that the system under consideration, which consists of electrical resistors of the same size and in parallel, the j-th resistor
can be regarded as a probability. Furthermore, recall that the system under consideration, which consists of electrical resistors of the same size and in parallel, the j-th resistor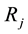 , is given by
, is given by
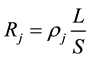 (2)
(2)
where 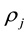 is the resistivity,
is the resistivity, 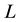 is the length and
is the length and 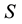 the section area. Define, now, the damage variable of the electrical system. Our idea is that as far as the resistors are solicited by the electric current, they are subject to degradation of some of their sections until the final break. Combining (1) and (2) yields
the section area. Define, now, the damage variable of the electrical system. Our idea is that as far as the resistors are solicited by the electric current, they are subject to degradation of some of their sections until the final break. Combining (1) and (2) yields
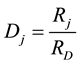 (3)
(3)
where  is the damage variable of the j-th resistor, and
is the damage variable of the j-th resistor, and 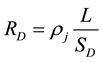 is the part of the resistor that has been
is the part of the resistor that has been
damaged. The Instantaneous resistor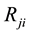 , is then given by
, is then given by
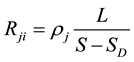 (4)
(4)
Using relations (2), (3) and (4), we can rewrite the resistor as 

Substituting expression (5) into (3), we are then able to define the damage variable 

With the initial condition: 




where 



We note that this expression is the product of two terms. The first one is already found in the case of independent (from a damage point of view) parallel components, and the associated variable 

The second term, however, reflects the coupling or correlation between resistors of the parallel system, this fact is manifested by the product of each resistor by the damage variable to the other resistors.
In the transverse case, the system is considered as a network of resistors 

where 


As in the case of a longitudinal damage, expression (11) is formed by a product of two terms. The first has been derived for the case of systems with independent components (from a damage point of view). In this case, the associated damage variable 

The second term shows clearly the coupling or correlation between resistors, and then, the fact that the deterioration of each resistor necessarily affects the others. This manifests itself by the product of each resistor by the damage variables relative to the other resistors.
In what follows, we propose to exploit the experimental results relating to printed circuits with various conductive inks onto nonwoven textiles. This would allow us to illustrate the calculations and determine experimentally the overall system damage, in terms of the partials damages of the conductive lines measured individually at various stages of solicitations.
3. Application to Printed Circuit onto Nonwoven
In the above, we outlined the theoretical foundations of our approach concerned with the study of the electroconductive textiles damage. We propose in what follows to illustrate this approach and show its relevance. Indeed, we will exploit some experimental results relating to printed transmission lines with various conductive inks onto nonwovens substrate [17] [19] . The electrical properties of these fabrics have demonstrated the relevance of the application of such systems as sensors to collect vital signals relating to human subjects [2] . Surface tension and viscosity have a great impact on the performance of the printed circuit during the washing tests. The first affects the dispersion of the ink in the substrate, while high values of the second have as consequence to prevent its diffusion.
Screen printing was performed on a substrate called “Evolon”, using various conductive inks of different viscosities and percentages of silver, such as “Creative Materials (CMI 112-15)”, “DuPont 5025” and “DuPont 5096” (Figure 1).
Evolon is a spun-bonded hydro-entangled structure with fibers of Polyester and Nylon. It has a three dimensional structure with very fine fibers of 1.5 micron in diameter (Table 1). To create a mechanical barrier and to prevent the ink from wearing away during washing, the printed nonwoven fabrics were laminated using thermoplastic urethane (TPU) meltblown layer [19] .
The printed nonwoven fabrics were laminated using thermoplastic urethane (TPU) meltblown layer in order to secure the printed ink traces in place and to make them durable to washing. Indeed, the lamination has as role to create a mechanical barrier and to prevent the ink from wearing away during washing. In addition, this coating of the transmission lines improves the durability properties without sacrificing the flexibility or the breathability of the substrate. The layer has a thickness of 40 - 50 microns, and is composed of fine fibers (with diameter of 5 microns) with very fine pores (less than 2 microns). These later create a microporous structure which passes the moisture vapor and blocks the fluids [19] .
In this experimental study [19] , the printed nonwoven substrates were exposed to numerous wash cycles in order to determine the durability properties. The printed inks begin to degrade after many wash cycles. The lines in Evolon showed micro-fractures and the printed traces were broken after washing. However less visible creases were observed due to its flexible structure. Electrical properties of the three printed lines were tested before and after washing (values of the resistance of each line) [19] (Table 2).
The first comment to make about these results is that the Creative Materials ink, having the highest viscosity due to its high content of silver, offers the best conductivity. Indeed, it has the lowest resistance before and after washing in comparison with the other inks. Furthermore, the resistances of the three conductive lines submitted to a direct electric current, increases after washing. This is attributed to high percentages of fractures on the ink surface due to the various stresses to which the conductive lines are submitted during washing (Torsion, crumpling, solvent effect, etc.).
Figure 1. The three kinds of inks printed on Evolon substrate [19] .
Table 1. Characteristics of Evolon substrate [19] .
Table 2. DC resistance values of Evolon before and after washing [19] .
We propose, now, to use these results to determine the partial damages




where 





Using expression (8), we can now to determine the overall damage 

where 


We report in Figure 2, three curves representing the overall longitudinal damage of the textile sheet for various inks.
The printed samples (each having three resistors corresponding to conductive lines) were submitted to numerous washing cycles. The deterioration of the inks quality leads to a variation of the conductivity of the transmission lines. This has the effect to reduce their ability to transmit the electrical signal, and therefore, the adjacent resistors are affected. Figure 2 shows that Creative Materials ink present a damage slowdown between
Table 3. Partial damages of the printed lines and the overall damage of the three textile sheets for different inks.
Figure 2. Overall damages of the three textile sheets for different inks.
15 and 25 wash cycles. Indeed its high viscosity and its better conductivity give this ink greater stability. However, with “DuPont 5096” ink, the printed transmission lines were completely deteriorated beyond 25 washing cycles. Although they present a low rate of fractures to 5 wash cycles, the damage of the printed textile sheet with “DuPont 5025” ink has accelerated brutally between 5 and 15 wash cycles. But they kept, ultimately, a damage rate located between the other two inks.
4. Concluding Remarks
In this work, the purpose is the determination of the damage of a special class of electro-conductive textiles, namely, the printed nonwovens textile substrates, which are subjected to external factors (electrical current, temperature change, frequent washing, etc.). In fact, the printed circuits boards continue to be a high growth technology in the area of electrical interconnectivity. Over traditional rigid printed circuit boards (PCB’s), wire and wire harnesses, flexible circuit boards provide considerable weight, space, and cost savings. To investigate the damage phenomenon, we determine an explicit expression of the overall damage variable, in terms of partial damages of the resistors forming the network. We first model the situation where the sample is under longitudinal solicitation (resistors connected in parallel). The transverse case for e-textiles in general is more complex, because the conductivity is provided by contacts between fibers. In this case, there exists a rate of contacts called percolation threshold, at which appears a continuous conductive path from one side to another of the sample. The study of such situations is performed, in general, in the framework of percolation theory introduced by Hamersley [24] -[26] . Nevertheless, we estimate that, in first approximation, the system can be modeled by a network of connected resistors in series. In obtained expressions of the overall damages 

In fact, we have used experimental results relating to printed nonwoven substrate called Evolon, which is exposed to numerous wash cycles in order to determine the electrical stability of transmission lines. This allows us to determine the overall damage in terms of those of printed lines for various inks. The damage curve shows, in particular, that high viscosity of Creative Material ink and its better conductivity give this ink greater stability.
Cite this paper
A.Maarouf,M.Chahid,M.Ouarch, (2015) Investigation of Electrical Stability of Nonwovens with Conductive Circuits Using Printed Conductive Inks. Journal of Textile Science and Technology,01,85-92. doi: 10.4236/jtst.2015.12009
References
- 1. Laurence, M., Kirstein, T. and Keller, T. (2004) Textile Electrodes for Transcutaneous Electrical Simulation. EMPA Conference Talk, Dubendorf.
- 2. Kang, T., Merritt, C.R., Karaguzel, B., Wilson, J.M., Franzon, P.D., Pourdeyhimi, B., Grant, E. and Nagle, T. (2006) Sensors on Textile Substrates for Home-Based Healthcare Monitoring. Conference on Distributed Diagnosis and Healthcare (D2H2), Arlington, 2-4 April 2006, 5-7. http://www.ece.ncsu.edu/erl/html2/papers/paulf/2006/paulf_2006_kang.pdf
- 3. Locher, I., Klemm, M., Kirstein, T. and Troster, G. (2006) Design and Characterization of Purely Textile Patch Antennas. Transactions on Advanced Packaging, 29, 777-788.
- 4. Locher, I. and Troster, G. (2007) Fundamental Building Blocks of Circuits on Textiles. IEEE Transactions on Advanced Packaging, 30, 541-550. http://dx.doi.org/10.1109/TADVP.2007.898636
- 5. Xue, P., Tao, X., Leun, M.Y. and Zhang, H. (2007) Wearable Electronics and Photonics. Woodhead Publishing Company, Cambridge, 81-103. http://www.e-library.esut.edu.ng/uploads/pdf/5407661245-wearable-electronics-and-photonics.pdf
- 6. Gasana, E., Westbroek, P., Hakuzimana, J., De Clerck, K., Kiekens, G. and Tseles, D. (2006) Electroconductive Textile Structures through Electroless Deposition of Polypyrrole and Copper at Polyaramide Suifaces. Surface & Coatings Technology, 201, 3547-3551. http://www.sciencedirect.com/science/article/pii/S0257897206009467
- 7. Banaszczk, J., De Mey, G., Schwarz, A. and Van Langenhove, L. (2009) Current Distribution Modelling in Electrocon- ductive Fabrics. Fibers and Textiles in Eastern Europe, 17, 28-33.
- 8. Hersh, S.P. and Mongomery, D.J. (1952) Electrical Resistance Measurements on Fibers and Fiber Assemblies. Textile Research Journal, 22, 805-818. http://dx.doi.org/10.1177/004051755202201207
- 9. Zieba, J. and Frydrysiak, M. (2006) Textronics—Electrical and Electronic Textiles Sensors for Breathing Frequency Measurement. Fibers & Textiles in Eastern Europe, 14, 43-48.
- 10. Oh, K.W., Park, H.J. and Kim, S.H. (2003) Strechable Conductive Fabric for Electrotherapy. Journal of Applied Polymer Science, 88, 1225-1229. http://dx.doi.org/10.1002/app.11783
- 11. Asanovic, K.A., Mihajlidi, T.A., Milosavljevic, S.V., Cerovic, D.D. and Dojcilovic, J.R. (2007) Investigation of the Electrical of Some Textile Materials. Journal of Electrostatics, 65, 162-167. http://dx.doi.org/10.1016/j.elstat.2006.07.008
- 12. Flandin, L., Brechet, Y. and Cavaille, J.Y. (2001) Electrically Conductive Polymer Nanocomposites as Deformation Sensors. Composites Science and Technology, 61, 895-901.
- 13. Krupa, I., Novak, I. and Codak, I. (2004) Electrically and Thermally Conductive Polyethylene/Graphite Composites and Their Mechanical Properties. Synthetic Metals, 145, 245-252. http://dx.doi.org/10.1016/j.synthmet.2004.05.007
- 14. Omastovà, M., Kosina, S., Pionteck, J. and Pavlinec, A. (1996) Electrical Properties and Stability of Polypyrrole Containing Conducting Polymer Composites. Synthetic Metals, 81, 49-57. http://dx.doi.org/10.1016/0379-6779(96)80228-1
- 15. Cochrane, C., Koncar, V., Lewandowski, M. and Dufour, C. (2007) Design and Development of a Flexible Strain Sensor for Textile Structures Based on a Conductive Polymer Composite. Sensors, 7, 473-492.
- 16. Le Maitre, J. and Chaboche, J.L. (2001) Mécanique des Matériaux Solides. Dunod, Paris.
- 17. Karaguzel, B., Merritt, C.R., Kang, T., Wilson, J.M., Nagle Jr., H.T. and Grant, E. (2008) Utility of Nonwovens in the Production of Integrated Electrical Circuits via Printing Conductive Inks. Journal of the Textile Institute, 99, 37-45. http://dx.doi.org/10.1080/00405000701547748
- 18. Suh, M., Carroll, K.E., Grant, E. and Oxenham, W. (2013) Effect of Fabric Substrate and Coating Material on the Quality of Conductive Printing. Journal of the Textile Institute, 104, 213-222. http://dx.doi.org/10.1080/00405000.2012.714107
- 19. Karaguzal, B. (2007) Printing Conductive Inks on Nonwovens: Challenges and Opportunities. PhD Thesis, North Carolina State University, Raleigh.
- 20. Maarouf, A., Chahid, M. and Benhamou, M. (2011) Damage of Composite Systems with Correlated Parts: Applications to Unidirectional Composite Materials. International Journal of Academic Research, 3, 722-728.
- 21. Schueler, R., Joshi, S.P. and Schulte, K. (1997) Conductivity of CFRP as a Tool for Health and Usage Monitoring Smart Structures and Materials. SPIE Proceedings, 3041, 417-426.
- 22. Jellid, J. (2009) Suivi du Cycle de Vie d’un Composite CFRP Hybride par Mesure de Résistance Electrique. PhD Thesis, Ecole Centrale de Lyon, écully.
- 23. Chahid, M., Benhamou, M., El Ghorba, M. and Azari, Z. (1996) Matériaux & Techniques, No. 11, 12.
- 24. Stauffer, D. and Aharony, A. (2003) Introduction to Percolation Theory. Taylor & Francis, London.
- 25. Bunde, A. and Dietrich, W. (2000) Percolation in Composites. Journal of Electroceramics, 5, 81-92.
- 26. Sahimi, M. (1994) Applications of Percolation Theory. Taylor & Francis, London.
NOTES
*Corresponding authors.





