American Journal of Industrial and Business Management
Vol.3 No.5(2013), Article ID:36005,9 pages DOI:10.4236/ajibm.2013.35056
A Fuzzy Multicriteria Grade Cluster Analysis for the Budget Allocation of Tourism and Leisure Resources
![]()
1Department of Tourism and Hospitality, Taiwan Hospitality & Tourism College, Hualian, Taiwan; 2Department of Industrial Engineering and Management Information, Huafan University, New Taipei City, Taiwan.
Email: *lin@mail.tht.edu.tw, lin19590310@gmail.com
Copyright © 2013 Maw-Cherng Lin, Junn-Yuan Teng. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received June 26th, 2013; revised July 26th, 2013; accepted August 9th, 2013
Keywords: Tourism and Leisure Resources; Budget Allocation; Grade Cluster Analysis; Fuzzy MCDM
ABSTRACT
The fuzzy multicriteria grade cluster analysis model put forward by this study can objectively deal with the need priorities of tourism and leisure resources so the budget is allocated first to the projects which are in urgent need of money. Thus, the following situation can be avoided: in the traditional budget allocation of tourism and leisure resources, the tourism and leisure project submitted by all units are not partitioned off according to their different need grades but unfairly mixed together in evaluation, leaving the projects at high need grade unable promptly to obtain funds.
1. Introduction
Tourism projects have a close relation to people’s lives and the investment in them is significant. The government therefore should not make decisions using subjective judgment but should first undertake analysis of the objective evaluation criteria and then make impersonal decisions. The more reasonable the budget allocation worked out by a government, the higher the efficiency in the use of resources and the more benefits people will enjoy. Therefore, for a government, one important subject regarding tourism projects is how to allocate the budget effectively, especially in situations of financial difficulty, when it is vital to allocate the budget to the place where it is most needed and hence to maximize the function of a limited budget.
Because the number of tourism projects varies in different departments, and the priority and urgency of the projects are different as well, thus, it is very difficult to allocate the budget effectively. Under such circumstances, the methods most commonly used are equalitarian allocation and allocation based on the size of both the population of units or local governments and the region they govern. These methods may result in the problem that the units bold enough to claim that it could be granted a greater budget, while those requesting nothing will be given little. However, the tenet of budget allocation is to make the most effective use of resources and where a budget is limited, to get it to where it is most needed, otherwise the problem might arise that some units are busy dealing with a budget exceeding their demand, but others are faced with the issue of an insufficient budget. Therefore, for a government, one of the most important subjects in its governance is how to allocate a budget based on the need priorities of tourism projects, while taking into consideration, for example, the environmental conservation, land planning and financial load.
The selection of tourism projects has several characteristics, such as multi-objectives, multi-attributes and multicriteria. These criteria can be considered relative to society, economy, finance, human resources, environment, market, and politics. Due to their potential to clash, and their variability, comparability and correlation, various criteria shall be evaluated and selected using a Multiple Criteria Decision-Making method (MCDM) instead of only the Cost-Benefit Analysis (CBA) or Single-objective Mathematical Programming method. Bellmen and Zadeh (1970) pioneered the exploration of the decisionmaking issue in a fuzzy environment [1], while Baas and Kwakernaak (1997) proposed to use preferred fuzzy sets as the method of ranking alternatives [2]. There are many methods for implementing a fuzzy multicriteria decision making method (fuzzy MCDM). For example, Chen and Hwang (1993) made a distinction and classification for each method besides fuzzy ranking and fuzzy multiple attribute decision-making methods [3]; Buckley (1985) came up with the Fuzzy Analytic Hierarchy Process method (Fuzzy AHP), which fuzzed the paired comparison values in Saaty’s AHP method and worked out the fuzzy weights of each evaluation dimension and evaluation criterion with a geometric mean method [4].
Much research on MCDM methods is in progress, covering electric power energy development programming [5], ranking of urban transportation investment alternatives [6], evaluation of sightseeing risk factors [7] and the marketing strategy of the electronics industry [8]. In particular, in transportation construction, this method was used by Huang et al. (2003) to assess the competitive abilities of ports [9] and by Pearman et al. (1989) to rank road investment programming [10]; the AHP method was utilized to evaluate the influence of constructing an expressway and the selection of contractors or procurement methods [11-16]. For the subject of budget allocation, Kwak & Diminnie (1987) resorted to a goal programming model to research the budget allocation of academic units [17]; Sundberg et al. (1989) to explore the allocation mechanisms in public provision of transport and communication infrastructure [18]; Ramanathan & Ganesh (1995) applied the AHP method to resource allocation [19]; Perng et al. (2007) used the Genetic Algorithm (GA) to solve the budget allocation in the restoration of historical buildings [20]; Han et al. (2005) adopted a non-linear programming model to figure out the optimal financial budget for software development plans [21]; Karydas and Gifun (2006) applied multi-attribute utility theory to the budget allocation of the infrastructure renewal programmes on university campuses [22]; the governments responded to actual or potential investments in tourism development [23,24]. In these studies, fuzzy MCDM was applied to unquantifiable or non-qualitative evaluation projects and yielded the required results.
In the use of the multivariate cluster analysis method in the present study, the major task is to find a clustering result [25] that the difference is small within a cluster and big among clusters in order to classify tourism projects with different need priorities. Moreover, the similarity in need priority ought to be high among the tourism projects from the same cluster and low among the tourism projects from different clusters. Thus, it would be easy to distinguish the tourism projects with different need priorities. As to the multivariate cluster analysis method, many studies have covered marketing research [26], organisational behaviour [27], landscape and ecological-condition classification [28], and land classification and management [29]. However, in these papers, we have been unable to find any subjects in which this analysis method was used to solve the problem for the resource allocation of tourism projects, so the related research in this paper is worthwhile.
Based on the systematic concept of budget allocation of tourism projects and the fuzzy quality (Bellman, 1970) of human beings in decisionand judgment-making, this paper will adopt fuzzy sets theory, the multivariate cluster analysis method and selection criteria for tourism projects to construct a fuzzy multicriteria grade cluster analysis model which will help to classify tourism projects into several grades in accordance with their priorities. Thus, objectively speaking, the projects that are urgently in need of money can be allocated the budget first.
This paper consists of three parts: Connotation and Use Steps of the Fuzzy Multicriteria Grade Cluster Model; Application; Conclusion.
2. Fuzzy Multi-Criteria Grade Cluster Analysis Model
The first task in the budget allocation for tourism construction is to determine the priority of execution among tourism projects. This paper will solve the problem of priority in executing tourism projects with fuzzy multicriteria grade cluster analysis theory. The tourism projects that are in most urgent need of money will be allocated the budget first, while the decision whether those that are the least urgent are allocated funds depends on whether there is a balance. Subsequently, we will show the grade cluster analysis method and the steps in the use of fuzzy MCDM and multivariate cluster analysis theory:
Step 1: List all tourism plans to be evaluated.
List n tourism plans: 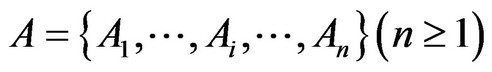
Step 2: Constitute a decision-making group (the evaluation committee).
Selecting t committee members to constitute a decision-making group: 
Step 3: Formulate evaluation criteria.
Formulating m evaluation criteria: 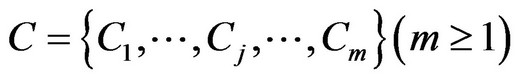
Step 4: Distinguish the clusters based on need grades.
The organiser has to discuss with the decision-making group the plans and budget amount of the present year to work out P need grades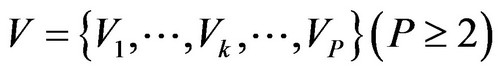 ; furthermore, the priorities of the need grades decrease in turn (i.e.,
; furthermore, the priorities of the need grades decrease in turn (i.e., 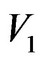 means that it is the most needed and
means that it is the most needed and  represents that it is the least needed).
represents that it is the least needed).
Step 5: Determine the weights of evaluation criteria.
Determining the importance of m evaluation criteria; the experts from the related fields in the decision-making group can assign the corresponding weights: 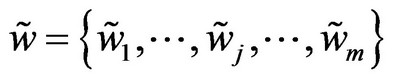
Step 6: Establish an Evaluation Matrix.
In light of the judgment and weighting made by the evaluation committee members, the fuzzy evaluation matrix 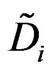 for each tourism project Ai under the evaluation criteria
for each tourism project Ai under the evaluation criteria  can be formulated as follows:
can be formulated as follows:
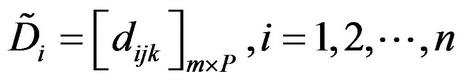 (1)
(1)
In the formula, 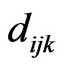 indicates the fuzzy performance value of Ai at the grade of
indicates the fuzzy performance value of Ai at the grade of 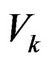 under the evaluation criteria
under the evaluation criteria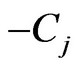 .
.
The evaluation criteria for tourism projects are all qualitative principles that cannot be easily measured with definite numerical values, so it is necessary to constitute the evaluation committee containing related experts, and then each committee member can make a judgment in accordance with the need grade of every tourism project under each evaluation criterion. Each member is allowed to check one within P grades under each criterion.
Supposing that there are T members in the evaluation committee, the fuzzy performance value 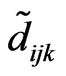 of each tourism project at each need grade under each criterion can be obtained through the following formula.
of each tourism project at each need grade under each criterion can be obtained through the following formula.
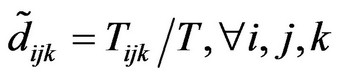 (2)
(2)
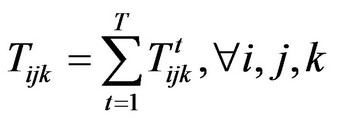 (3)
(3)
 (4)
(4)
 (5)
(5)
 (6)
(6)
Step 7: Calculate the fuzzy evaluation vector after the weighting.
When considering m evaluation criteria simultaneously, we can calculate the following fuzzy evaluation vector 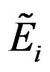 after the weighting.
after the weighting.
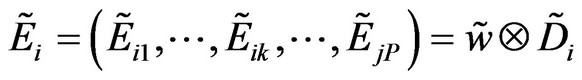 (7)
(7)
In the formula,
 (8)
(8)
 (9)
(9)
Step 8: Grade Cluster Classification.
Since 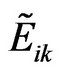 stands for the fuzzy judgment value when the tourism project Ai is comprehensively appraised as Grade k under m evaluation criteria, so the priority sequence of tourism projects is the result of the grade cluster classification of n tourism projects A1, A2, ∙∙∙, An with
stands for the fuzzy judgment value when the tourism project Ai is comprehensively appraised as Grade k under m evaluation criteria, so the priority sequence of tourism projects is the result of the grade cluster classification of n tourism projects A1, A2, ∙∙∙, An with  known.
known.
1) Defuzzification Through the above comprehensive evaluation of fuzzification, we can obtain the triangular fuzzy numbers of each tourism project. These fuzzy numbers are not definite numerical values, so they must be defuzzified; spe cifically, the best non-fuzzy performance value (BNP) has to be found. In the literature, there are many methods for defuzzification, such as Middle of Maxima (MOM), Centre of Area (COA) and α-cut set. This paper adopts Centre of Area (COA) [6] to implement defuzzification because this method is simple to use and the preference of evaluation committee members need not be considered. The BNPi value of fuzzy numbers can be calculated with the following formula:
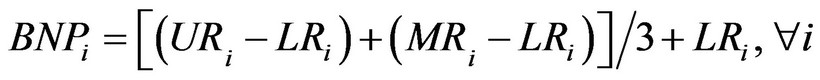 (10)
(10)
2) Setting of the distance among clusters Before analysing the clusters, we need to work out the dissimilarity or similarity among the clusters in light of the variables. At present, the dissimilarity can be expressed with several distance measures, such as Euclidean distance, squared Euclidean distance, size difference distance, pattern difference distance, variance distance, shape distance, and Lance and Williams distance [30]. This paper uses squared Euclidean distance to perform the analysis. Setting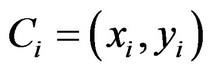 ,
,  , the squared Euclidean distance between
, the squared Euclidean distance between 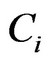 and
and 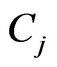 is:
is:
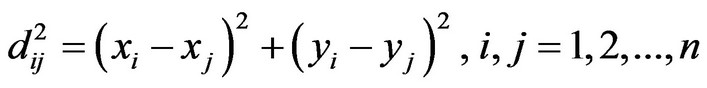 (11)
(11)
Therefore, the squared Euclidean distance of clusters can be written as follows:
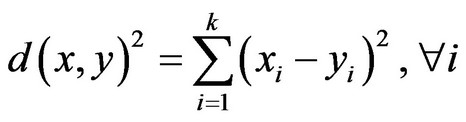 (12)
(12)
3) Hierarchical Analysis Method The analysis methods are usually divided into hierarchical and nonhierarchical methods; moreover, the hierarchical methods can also be sub-divided into agglomerative and divisive methods. In the agglomerative method, the distance among observed objects or the error matrix within a group is calculated first, and then the two closest observed objects are merged into a cluster; next, the distance among merged observed objects or the error matrix within a group is computed. The above procedure is repeated until all observed objects are merged into the same cluster. The most commonly used methods include the single linkage method, the complete linkage methodthe average linkage method, the centroid method, the median method and Ward’s method. In the past, most studies have shown that the average linkage method and Ward’s method are the better methods [31]. After trying all analysis methods, we found that the average linkage method leads to an ideal result. The steps are as follows:
1) Find out the two closest tourism-project clusters (also called observed objects); for example, CA and CB are merged into CAB.
2) Calculate the distance between the new tourismproject cluster CAB and other tourism-project clusters:
 (13)
(13)
This formula indicates that the average distances between CA and CD and between CB and CD are used as the new distance between CAB and CD; n represents all logarithms between the two tourism-project clusters CAB and CD. The average distance between A and B (the tourism-project clusters) can be further written as:
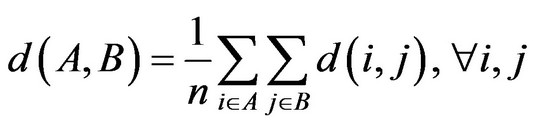 (14)
(14)
3) Repeat the above steps until all observed objects are merged into one cluster.
Step 9: Grade Classification for all Tourism Projects.
According to the results of analysing the above infrastructure-project clusters and 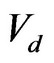 (the need of the clusters with P grades determined by the evaluation committee), the cut-off point
(the need of the clusters with P grades determined by the evaluation committee), the cut-off point 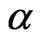 can be selected to classify all tourism projects into different grades, as the following formula shows:
can be selected to classify all tourism projects into different grades, as the following formula shows:
If 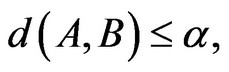 then
then  (15)
(15)
and 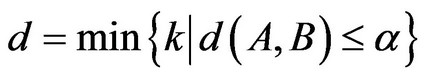 (16)
(16)
3. Application
3.1. Explanation of Decision-Making Problem
Suppose a ministry of the tourism of Taiwan is composed of six units which are respectively symbolized with A, B, C, D, E and F; they submit a total of 26 tourism projects in a fiscal year, including 3 from A, 3 from B, 11 from C, 3 from D, 4 from E and 2 from F; The budget each project needs is listed in Table 1. Although the total budget these projects need amounts to NT$17.279 billion, the actual budget that is available that year is not more than NT$10 billion, which cannot simultaneously meet the demand of the six units. In this situation, the governmental department is faced with the decision-making problem of how to allocate the available budget and how to decide which projects ought to be executed.
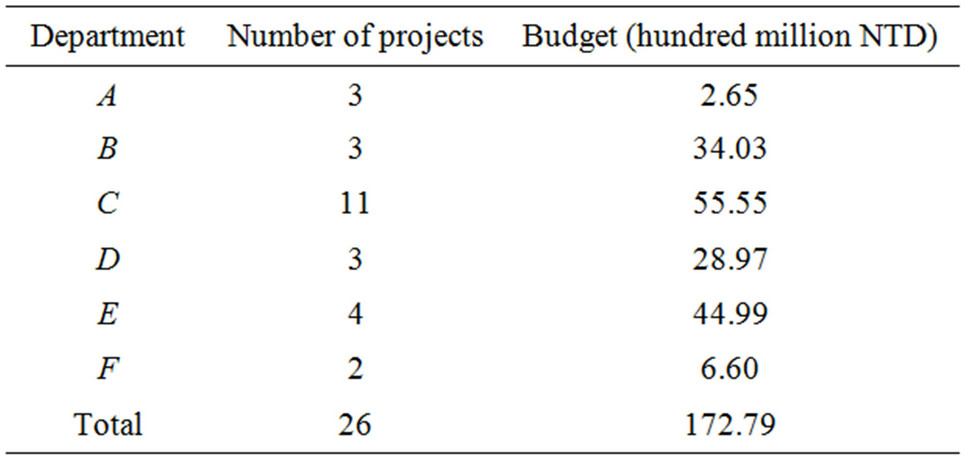
Table 1. The number of projects proposed by six governmental departments and budgets needed.
3.2. The Formulation of Evaluation Criteria and the Determination of Weighting
In order to facilitate the evaluation of budget allocation for the projects submitted by each unit, the governmental department first formulates a set of evaluation criteria accepted by each unit. The results of the investigation and analysis undertaken by the department indicate that these criteria consist of 4 evaluation dimensions and 10 evaluation indices. In terms of weighting, the calculation is performed on the basis that the total weight is 1. The details are shown in Table 2.
In order to simplify the evaluation work, this governmental department uses the fuzzy multicriteria grade cluster model proposed by this paper to classify the tourism projects into different grades in light of their need priorities. To begin with, an evaluation committee with 12 members is constituted, and these members include the organiser, supervision units from the tourism department, units directly subordinate to the central government, schoolars and experts; they will make their judgments based on the need priorities of projects under the 10 evaluation criteria and check the grade they think is appropriate according to the prospectus, field surveys and briefings submitted by each unit.
3.3. Grade Classification of the Need Priority of Tourism Projects
3.3.1. Comprehensive Evaluation of the Need Priorities of Tourism Projects
After discussion with the evaluation committee, this governmental department classifies the tourism projects into five grades on the basis of need priority: “Urgently needed”, “Badly needed”, “Much needed”, “Rather needed” and “Little needed”. The first grade means that the project enjoys top priority, while the fifth grade indicates that the project is lowest in terms of need. The tourism project A101 submitted by Unit A is taken as an example; the corresponding results of its evaluation by the 12 committee members are shown in Table 3, in which the numbers are the comprehensive judgments made by the 12 members. According to the definition of fuzzy weighting, the 12

Table 2. The evaluation criteria of a governmental tourism project and their weights.

Table 3. Expert evaluation results for A101 tourism project.
evaluation members make comprehensive judgments and transform the definite values of BNP, as shown in Table 4, through the procedures of calculation and defuzzification. For instance, according to the comprehensive judgment results from the 12 committee members, under each evaluation criterion the tourism project A101 has the best non-fuzzy performance value (BNP), 326.43.
3.3.2. Grade Cluster Classification of the Need Priorities of Tourism Projects
Based on the BNP value of each tourism project calculated in the previous section, we obtain the dendrogram (Figure 1) through multivariate cluster analysis with SPSS software and with the between groups average linkage method, then according to the five need grades determined by this governmental department and the evaluation committee, the cut-off point can be selected to generate the five grade clusters, as shown in Table 5. In this table, 2 projects belong to Grade V1—“Urgently Needed”, 11 projects to Grade V2—“Badly Needed”, 12 projects to
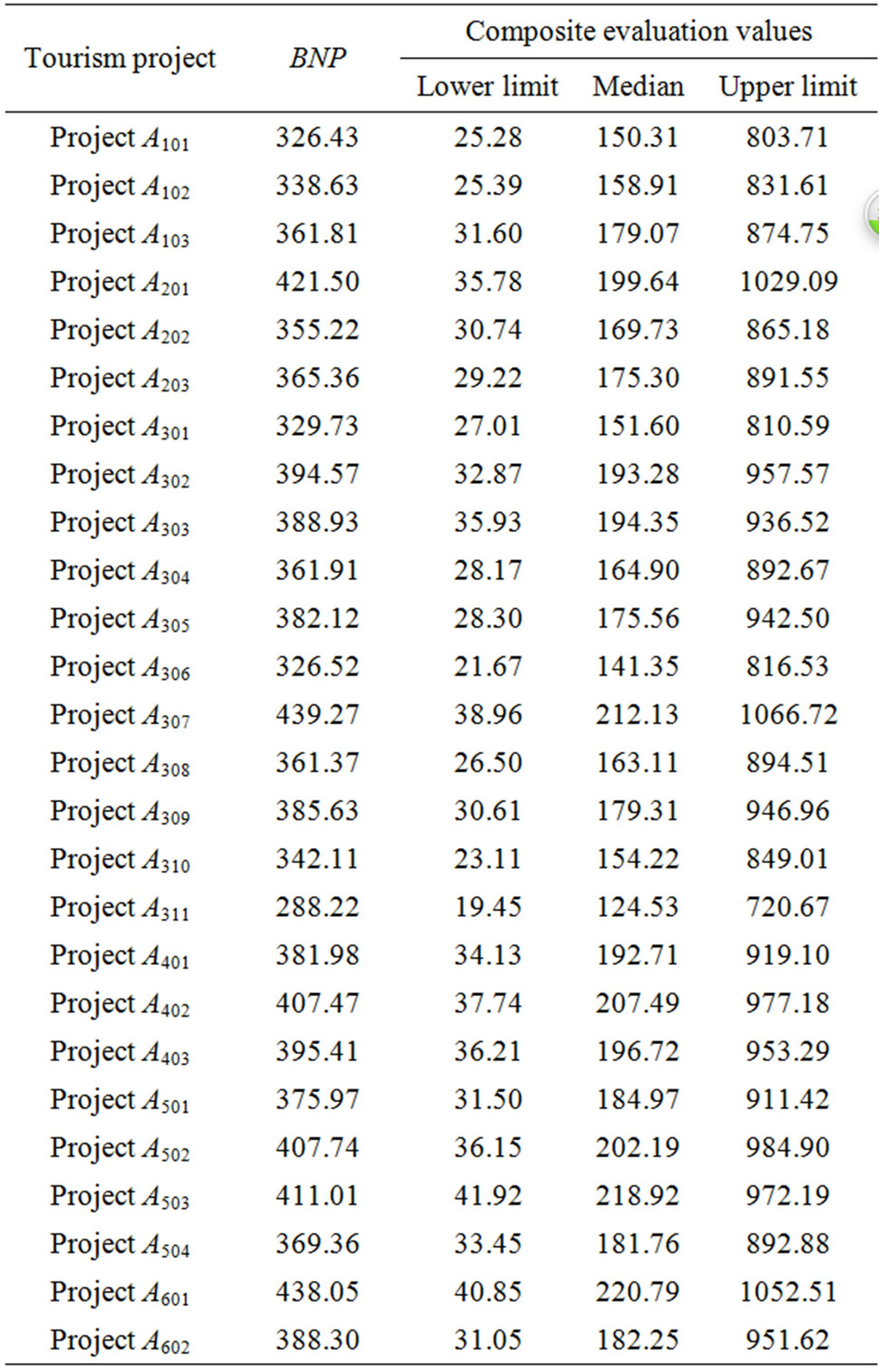
Table 4. BNP chart of fuzzy MCDM.
Grade V3—“Much Needed”, 1 project to Grade V4— “Rather Needed”, and no projects to Grade V5—“Little Needed”.
We can further calculate the budget needed by the tourism projects at each grade in accordance with the
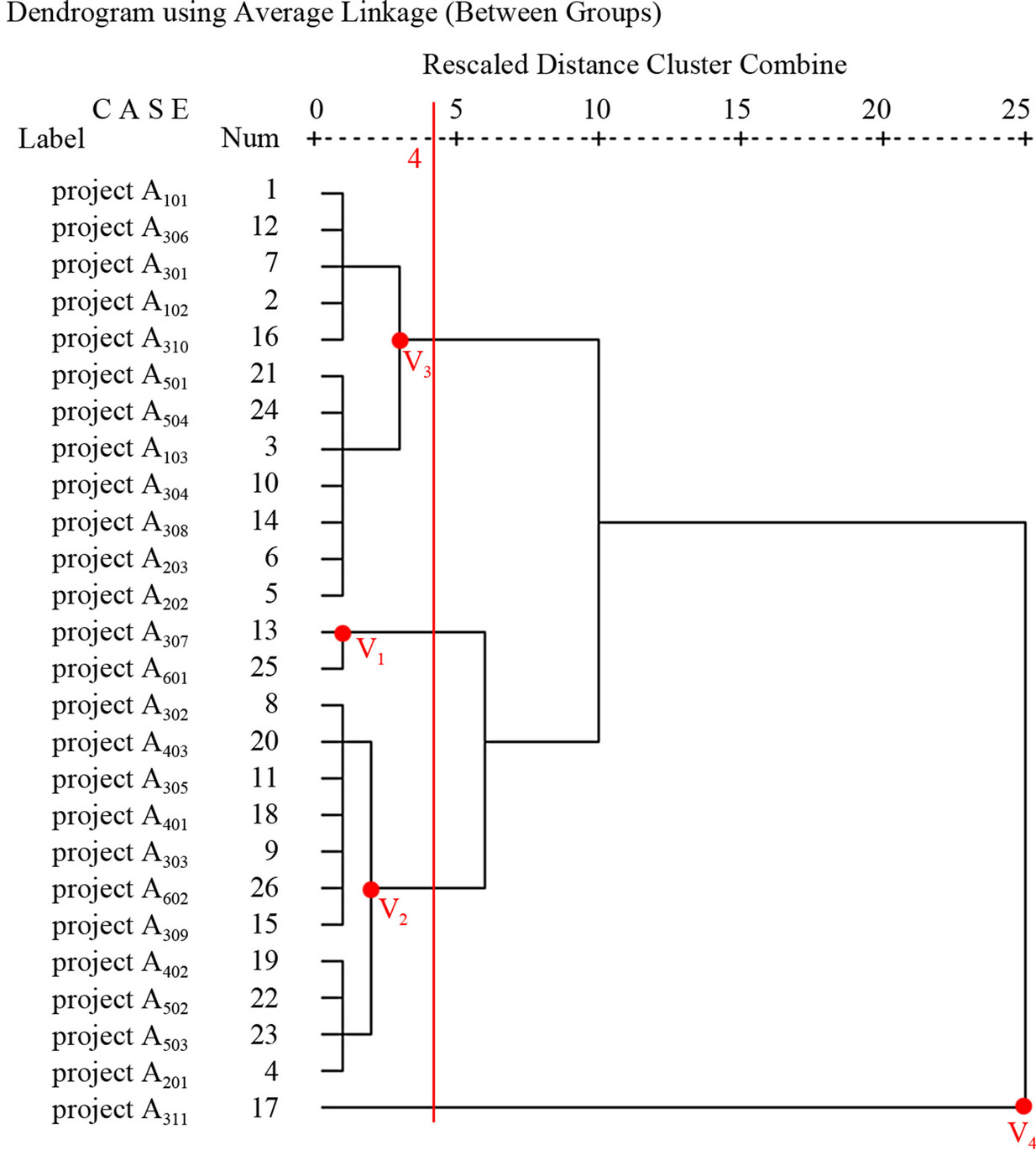
Figure 1. Dendrogram using Average Linkage, Between Groups.
data of the budget needed by projects, as Table 5 shows; the total amount is simply all the budget funds the tourism projects need at this grade. The details are listed in Table 6.
3.4. Results and Discussion
According to the above analysis results, we can discern which grade each tourism project belongs to; we can then resort to the fuzzy multicriteria ranking model and the budget allocation model to allocate the funds for tourism projects and the tourism budget for each unit on the basis of actual available total budget in the present fiscal year.
Essentially, the evaluation of tourism projects needs to follow the principle of multiperson multicriteria: not only should the evaluation criteria of cost, society, finance, market, environment, politics and management be taken into consideration, but how to evaluate the projects, how to select the committee members and how to decide the number of committee members cannot be ignored, either. More importantly, we should consider how to execute the budget allocation on the basis of the evaluation of tourism projects. However, to make a fair choice among the tourism projects instead of mixing together all the projects at different need grades in the evaluation constitutes a heavy workload for the organiser and committee members, especially when the budget is limited and there are many tourism projects with various need priorities.
The above theory and application example indicate that the members of the evaluation committee can make judgments under the formulated criteria and according to the five need grades—“Urgently Needed”, “Badly Needed”, “Much Needed”, “Rather Needed” and “Little Needed”. In this way, the work involved in the evaluation of tourism projects can be significantly simplified. In particular, when all tourism projects are classified into several grades according to the need priorities, the projects in urgent need of money can be allocated the budget first to make effective use of limited resources.
4. Conclusion
In the budget allocation of tourism projects, instead of being unfairly mixed together in the evaluation, a number of tourism projects ought to be partitioned off in light of their different need grades, which could indeed help the government to relieve the heavy workload of making choices among so many tourism projects. Fuzzy theory can be used to investigate and deal with the weighting and judgment of experts on the need priorities of tourism

Table 5. Evaluation results for the tourism projects submitted by each department and the budget needed.

Table 6. Levels of tourism projects and budget needed.
projects, which could overcome the different needs of individual decision-making activities in the decisionmaking group. A follow-up fuzzy multicriteria grade cluster model will combine 2 sub-models—the fuzzy multicriteria ranking model and the budget allocation model—to construct a complete model for the budget allocation of tourism projects. The budget allocation methods brought forward in the future need to provide easy access to the analysis of sensitivity and meet the charging demands of response policies. In addition, in the construction of models, it is necessary to consider that the senior manager should have the right to use a certain proportion of the budget, in order to give him equivalent rights and responsibilities. Thus, the senior manager could significantly improve management efficiency and take the corresponding responsibility.
REFERENCES
- R. E. Bellman and L. A. Zadeh, “Decision-Making in a Fuzzy Environment,” Management Science, Vol. 17, No. 4, 1970, pp. 141-164. doi:10.1287/mnsc.17.4.B141
- S. M. Baas and H. Kwakernaak, “Rating and Ranking of Multiple Aspect Alternative Using Fuzzy Sets,” Automatica, Vol. 13, No. 1, 1997, pp. 47-58. doi:10.1016/0005-1098(77)90008-5
- S. J. Chen and C. L. Hwang, “Fuzzy Multiple Attribute Decision Making, Methods and Applications,” In: Lecture Notes in Economics and Mathematical Systems, Vol. 375, Springer, New York, 1993. doi:10.1016/0165-0114(85)90090-9
- J. J. Buckley, “Fuzzy Hierarchical Analysis,” Fuzzy Sets and Systems, Vol. 17, No. 1, 1985, pp. 233-247.
- G. H. Tzeng, T. A. Shiah and J. Y. Teng, “A Multiobjective Decision Making Approach to Energy Supply Mix Decisions in Taiwan,” Energy Sources, Vol. 16, No. 3, 1994, pp. 301-316. doi:10.1080/00908319408909080
- J. Y. Teng and G. H. Tzeng, “Fuzzy Multicriteria Ranking of Urban Transportation Investment Alternatives,” Transportation Planning and Technology, Vol. 20, No. 1, 1996, pp. 15-31. doi:10.1080/03081069608717577
- S. H. Tsaur, G. H. Tzeng and G. C. Wang, “Evaluating Tourist Risks from Fuzzy Perspectives,” Annals of Tourism Research, Vol. 24, No. 4, 1997, pp. 796-812. doi:10.1016/S0160-7383(97)00059-5
- M. T. Tang, G. H. Tzeng and S. W. Wang, “A Hierarchy Fuzzy MCDM Method for Studying Electronic Marketing Strategies in the Information Service Industry,” Journal of International Information Management, Vol. 8, No. 1, 1999, pp. 1-22.
- W. C. Huang, J. Y. Teng, M. J. Huang and M. S. Kuo, “Port Competitiveness Evaluation by Fuzzy Multicriteria Grade Classification Model,” Journal of Marine Science and Technology, Vol. 11, No. 1, 2003, pp. 53-60.
- A. D. Pearman, “The Use of Multicriteria Techniques to Rank Highway Investment Proposals,” In: A. G. Lockett and G. Islei, Eds., Improving Decision Making in Organisations, Springer-Verlag, Berlin, 1989.
- I. J. Azis, “Analytic Hierarchy Process in the Benefit-Cost Framework: A Post-Evaluation of the TransSumatra Highway Project,” European of Operational Research, Vol. 48, 1990, pp. 38-48. doi:10.1016/0377-2217(90)90059-K
- K. M. Al-Subhi, “Application of the AHP in Project Management,” International Journal of Project Management, Vol. 19, No. 1, 2001, pp. 19-27. doi:10.1016/S0263-7863(99)00038-1
- M. I. Al Khalil, “Selecting the Appropriate Project Delivery Method Using AHP,” International Journal of Project Management, Vol. 20, No. 6, 2002, pp. 469-474. doi:10.1016/S0263-7863(01)00032-1
- S. W. Fong and S. K. Y. Choi, “Final Contractor Selection Using the Analytical Hierarchy Process,” Construction Management Economics, Vol. 18, No. 5, 2000, pp. 547-557. doi:10.1080/014461900407356
- T. Y. Hsieh, S. T. Lu and G. H. Tzeng, “Fuzzy MCDM Approach for Planning and Design Tenders Selection in Public Office Buildings,” International Journal of Project Management, Vol. 22, No. 7, 2004, pp. 573-584. doi:10.1016/j.ijproman.2004.01.002
- I. M. Mahdi, M. J. Riley, S. M. Fereig and A. P. Alex, “A Multi-Criteria Approach to Contractor Selection,” Engineering Construction and Architectural Management, Vol. 9, No. 1, 2002, pp. 29-37.
- N. K. Kwak and C. B. Diminnie, “A Programming Model for Allocating Operating Budgets of Academic Units,” Socio-Economic Planning Sciences, Vol. 21, No. 5, 1987, pp. 333-339. doi:10.1016/0038-0121(87)90007-3
- L. Sundberg and G. Carlen, “Allocation Mechanisms in Public Provision of Transport and Communication Infrastructure,” Regional Science, Vol. 23, No. 4, 1989, pp. 311-327. doi:10.1007/BF01579782
- R. Ramanathan and L. S. Ganesh, “Using AHP for Resource Allocation Problems,” European Journal of Operational Research, Vol. 80, No. 2, 1995, pp. 410-417. doi:10.1016/0377-2217(93)E0240-X
- Y. H. Perng, Y. K. Juan and H. S. Hsu, “Genetic Algorithm-Based Decision Support for the Restoration Budget Allocation of Historical Buildings,” Building and Environment, Vol. 42, No. 2, 2007, pp. 770-778. doi:10.1016/j.buildenv.2005.09.009
- Y. Han, X. Wu and C. Yue, “Optimizing Financial Budget for Software Implementation Based on the Development Effort and Cost Function,” Advances in Engineering Software, Vol. 36, No. 10, 2005, pp. 699-706. doi:10.1016/j.advengsoft.2004.10.001
- D. M. Karydas and J. F. Gifun, “A Method for the Efficient Prioritization of Infrastructure Renewal Projects,” Reliability Engineering & System Safety, Vol. 91, No. 1, 2006, pp. 84-99. doi:10.1016/j.ress.2004.11.016
- D. A. Tommy and G. Donald, “Tourism as a Mixed Industry: Differences between Private, Public and Not-forProfit Festivals,” Tourism Management, Vol. 30, No. 6, 2009, pp. 847-856. doi:10.1016/j.tourman.2008.12.008
- J. A. Puppim de Oliveira, “Governmental Responses to Tourism Development: Three Brazilian Case Studies,” Tourism Management, Vol. 24, No. 1, 2003, pp. 97-110. doi:10.1016/S0261-5177(02)00046-8
- D. L. Davies and D. W. Bouldin, “A Cluster Separation Measure,” IEEE Transactions on Pattern Analysis and Machine Intelligence, Vol. 1, No. 2, 1979, pp. 224-227. doi:10.1109/TPAMI.1979.4766909
- C. Bakewell and V. L. Mitchell, “Generation Y Female Consumer Decision-Making Style,” International Journal of Retail & Distribution Management, Vol. 31, No. 2-3, 2003, pp. 95-106. doi:10.1108/09590550310461994
- P. R. Sparrow and K. Gaston, “Generic Climate Map: A Strategic Application of Climate Survey Data?” Journal of Organisational Behaviour, Vol. 17, No. 6, 1996, pp. 679-698. doi:10.1002/(SICI)1099-1379(199611)17:6<679::AID-JOB786>3.0.CO;2-M
- D. J. Briggs and J. France, “Classifying Landscape and Habits for Regional Environmental Planning,” Journal of Environmental Management, Vol. 17, 1983, pp. 249-261.
- J. F. Calvo, J. A. Palazon, M. A. Esteve, M. L. Suarez, A. Torres, M. R. Vidal-Abarca and L. Ramirez-Diaz, “The Use of Multivariate Analysis for the Ecological Characterization of Landscape: The Mula River Watershed, South-East Spain,” Journal of Environmental Management, Vol. 34, No. 4, 1992, pp. 297-308. doi:10.1016/S0301-4797(11)80005-8
- SPSS, “SPSS 10 Syntax Reference Guide,” SPSS, Chicago, 1999.
- G. W. Milligan, “An Examination of the Effect of Six Types of Error Perturbation on Fifteen Clustering Algorithms,” Psychometrika, Vol. 45, No. 3, 1980, pp. 325- 342. doi:10.1007/BF02293907
NOTES
*Corresponding author.

