Open Journal of Medical Imaging
Vol.05 No.03(2015), Article ID:59483,9 pages
10.4236/ojmi.2015.53017
Dynamic Image Prediction Using Principal Component and Multi-Channel Singular Spectral Analysis: A Feasibility Study
Ritu Bhusal Chhatkuli1, Kazuyuki Demachi2, Naoki Miyamoto3, Mitsuru Uesaka2, Akihiro Haga4*
1Department of Bioengineering, The University of Tokyo, Tokyo, Japan
2Nuclear Professional School, The University of Tokyo, Tokyo, Japan
3Department of Medical Physics, Hokkaido University Hospital, Sapporo, Japan
4Department of Radiology, The University of Tokyo Hospital, Tokyo, Japan
Email: *haga-haga@umin.ac.jp
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 8 July 2015; accepted 6 September 2015; published 9 September 2015
ABSTRACT
Respiratory motion induces the limit in delivery accuracy due to the lack of the consideration of the anatomy motion in the treatment planning. Therefore, image-guided radiation therapy (IGRT) system plays an essential role in respiratory motion management and real-time tumor tracking in external beam radiation therapy. The objective of this research is the prediction of dynamic time- series images considering the motion and the deformation of the tumor and to compensate the delay that occurs between the motion of the tumor and the beam delivery. For this, we propose a prediction algorithm for dynamic time-series images. Prediction is performed using principal component analysis (PCA) and multi-channel singular spectral analysis (MSSA). Using PCA, the motion can be denoted as a vector function and it can be estimated by its principal component which is the linear combination of eigen vectors corresponding to the largest eigen values. Time- series set of 320-detector-row CT images from lung cancer patient and kilovolt (kV) fluoroscopic images from a moving phantom were used for the evaluation of the algorithm, and both image sets were successfully predicted by the proposed algorithm. The accuracy of prediction was quite high, more than 0.999 for CT images, whereas 0.995 for kV fluoroscopic images in cross-correlation coefficient value. This algorithm for image prediction makes it possible to predict the tumor images over the next breathing period with significant accuracy.
Keywords:
Radiation Therapy, Lung Tumor, Markerless, Image Prediction, Tracking

1. Introduction
Respiratory motion management has been a major challenge in radiation therapy especially for lung cancer with the large amplitude of motion in lungs being clinically significant [1] . Confining the radiation to the target and reducing the unnecessary high dose to the healthy tissues still remain a major concern in modern radiation therapy. In the case of moving tumors, the possible reduction of the internal margin becomes absolutely essential. Various strategies have been introduced in order to compensate the tumor motion, beam gating, active or volunteer breath hold, beam tracking, tracking with fiducial or infrared markers etc. [2] . Long-term breath-hold technique lacks the patient comfort, and beam gating and beam tracking require precise knowledge of the position of the tumor [3] . Gating using infrared or implanted markers have been popular treatment lately where the tumor is irradiated during a certain location. However, there are some disadvantages: a long treatment time due to inefficiency, an uncertainty in the correlation between the target and the marker motion, and invasive procedure for implanted marker. On the other hand, the tumor tracking radiation therapy is currently in applicable phase by means of the development of the image-guidance system. A modern image-guided radiation therapy (IGRT) system has made it possible to monitor the target motion during the external radiation therapy treatment. Most treatment machines are nowadays equipped with one or two kV X-ray source with flat panel detectors with the rotating or fixed gantry [4] and sometimes a robotic treatment couch [5] for the precise radiation delivery. With such a system, the sight of the tumor location can be adjusted based on the real-time X-ray images.
Even with the real-time monitoring, there exists a time delay between the beam irradiation and the motion of the target. This is mainly because the adaptive response of a radiotherapy system to a tumor position signal cannot occur instantaneously. Hence the beam cannot follow the target accurately [6] . If the time lag is filled with prediction of tumor position then the treatment beam can eventually follow the target. Predicting the position of the target in advance is considered as an approach to minimize positioning errors due to time lag in the system. The tumor tracking based on prediction of tumor position or motion using implanted or surface markers has already been introduced [7] [8] . However, the image prediction would be more direct for the lung tumor to consider non-rigid deformation that occurs due to the significant tumor mobility and elasticity of lung tissue [9] . Also, the predicted image can be used easily to verify the in-treatment accuracy by comparing with planning CT or its digitally reconstructed radiograph. Thus, the image prediction might contribute to the reduction of the internal margin during radiation therapy.
Principal component analysis (PCA) or eigen value analysis is a data feature extraction and data representation technique widely used in data analysis and compression [10] . In cooperation with multi-channel singular spectral analysis (MSSA), this can produce the future data based on the renewal knowledge from moment to moment. Lung motion model based on PCA has already been reported, which efficiently represents lung motion with few principal components [11] . On the other hand, these models have so far been used only for the image creation, and prediction has not been considered. In this paper, we propose a new algorithm for the prediction of lung motion images.
First, we examined with a four-dimensional CT (4DCT) image set. The CT image is convenient for the assessment of dynamic image prediction including the information of tumor deformation, but is not suitable for the real-time prediction because it is currently impossible to acquire the 4DCT images during treatment. Therefore, second, we examined with a kilovolt (kV) fluoroscopic image set, which can be handled in real time.
2. Dynamic Image Prediction System
2.1. Input Image Acquisition
2.1.1. Acquisition of Four Dimensional CT Images
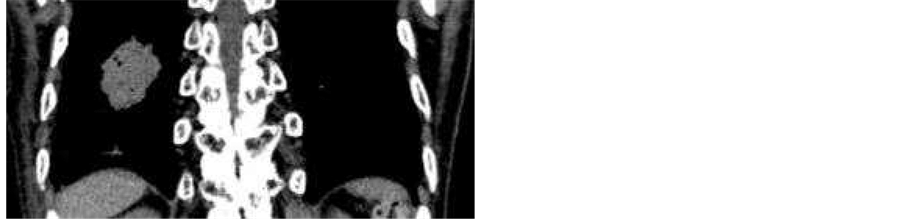
For the preliminary study of the image prediction, we employed a 4DCT image set obtained by AcquilionOneTM 320-detector-row CT device (Toshiba). An example of coronal slice used as input image is shown in Figure 1. This set was generated from a lung cancer patient over several breathing cycles. Total 28 CTs which were continuously acquired with the rate of 0.5 sec were taken and were divided into set of training images and test- ing images in order to verify our prediction algorithm. The voxel size of the CT was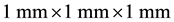 . In this study, the 28 images were repeated 5 times in order to increase the number of input data, and then, the last 10 CTs (5 sec) were assigned as the testing images.
. In this study, the 28 images were repeated 5 times in order to increase the number of input data, and then, the last 10 CTs (5 sec) were assigned as the testing images.
For the image prediction, we evaluated the accuracy in the limited view of 4DCT slice referred as large view
Figure 1. An example reconstructed coronal slice (large view 4DCT) used in the present study.
4DCT and its region of interest (ROI) i.e. only the tumor and its surrounding area. The pixel size of the large view 4DCT was 140 ´ 300 whereas for the ROI, it was 60 ´ 52.
2.1.2. Acquisition of Kilovolt X-Ray Fluoroscopic Images
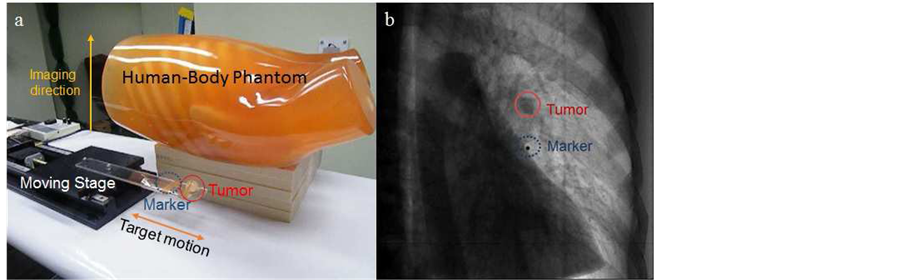
As second set of input images, kV fluoroscopic images from a linearly driven motion stage phantom were acquired. The phantom and the example of dynamic fluoroscopic images used in this study are illustrated in Figure 2(a) and Figure 2(b), respectively. The breathing cycle of the stage was set as 8 sec, and the corresponding amplitude was set as 60 mm. Total 24 images were sequentially acquired and were repeated for 4 cycles. The last 10 images were assigned as testing images similar to the 4DCT images mentioned in section 0. The imaging resolution was about 0.2 mm per pixel at the isocenter and the frame rate was 10 frames per sec.
The figure shows a mock tumor marked in red solid circle and the marker marked in blue dotted circle. We attempted two cases for the prediction of kV fluoroscopic images; the ROI from the image shown in Figure 2 with the size 121 ´ 323 including the tumor and the marker, and the size 79 ´ 174 including only the tumor. These were taken as the input images for the prediction algorithm mentioned in the next Section 2.
2.2. Prediction Algorithm
The algorithm for dynamic image prediction system is divided into three main steps as explained below.
2.2.1. Principal Component Calculation Using PCA
A set of input images with pixel size 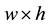 are considered. The 2D input images are converted into 1D image vectors, and then, a single matrix X is constructed by them as,
are considered. The 2D input images are converted into 1D image vectors, and then, a single matrix X is constructed by them as,
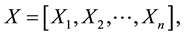 (1)
(1)
where n is the total number of input images for the training set. Next we calculate the auto-correlation matrix as shown in the Equation (2),
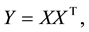 (2)
(2)
where T refers to transpose. Eigen analysis is then performed on Y resulting,
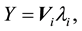 (3)
(3)
where V is the eigen vectors and 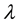 is the corresponding eigen value. When transforming the image to 1D image vectors, the resulting image vectors usually lead to a very high dimensional image vector space. This can be minimized by the eigen analysis on
is the corresponding eigen value. When transforming the image to 1D image vectors, the resulting image vectors usually lead to a very high dimensional image vector space. This can be minimized by the eigen analysis on 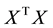 instead,
instead,
 (4)
(4)
Multiplying X on both sides, we get,
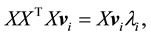 (5)
(5)
and this leads to,
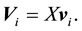 (6)
(6)
Figure 2. (a) The human-body and linearly driven motion stage phantom; (b) Input fluoroscopic image obtained from the phantom.
Equation (6) shows that the dimension of meaningful eigen vectors can only be considered instead of con- sidering the whole matrix. This is real with the very high correlation of consecutive frames in the time series images. The most dominant characteristics of the image are centralized on the highest eigen vector. Hence, in the equation, we setup the number of principal components as number i which denotes the number of dominant eigen vectors. The p eigen vectors 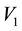 to
to 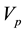 are then arranged into two dimensional matrices to form the prin- cipal component images as explained by the following,
are then arranged into two dimensional matrices to form the prin- cipal component images as explained by the following,
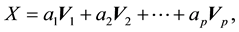 (7)
(7)
where  is the p-th principal coefficient and can be calculated as following,
is the p-th principal coefficient and can be calculated as following,
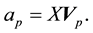
2.2.2. Coefficient Prediction Using MSSA
The coefficients calculated from PCA can be used for the prediction of future coefficient estimated by MSSA, which is an extended version to multi-dimensions from singular spectral analysis useful for analyzing non-linear time series [12] . The main step consists of construction of the trajectory matix and its singular value decom- position. We define a trajectory matrix for the coefficients obtained from PCA with time delay matrices as,
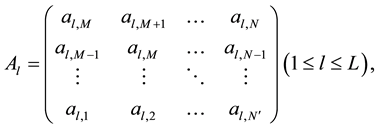
where arbitrary parameter M is known as the embedded dimension, l is one dimension in L dimensions and N is the number of coefficients using one prediction and 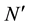
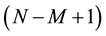
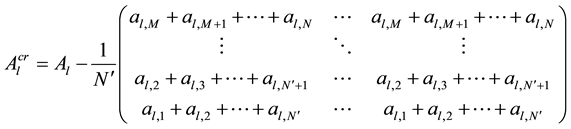
This Equation (10) can further be denoted as Equation (11),
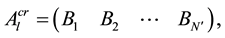
Auto-correlation matrix is defined with the above trajectory matrix and its transpose as,

where,
Eigen analysis is performed as in 2. We choose r (arbitrary number) largest eigen values and corresponding eigen vectors shown as,
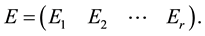
Using MSSA, we can predict the future data using this E from the equation for principal components of previous time series data. Actually, we create 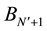
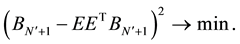
This denotes that 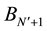
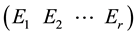
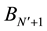

where 
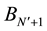

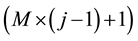
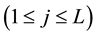
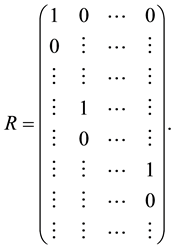
According to Equation (14) and Equation (15) we can evaluate P as,
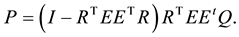
We can obtain the L unknown future data by solving the condition and setting back the centering values,

2.2.3. Image Reformation Using PCA
Once the coefficients are predicted, the predicted image can be reformed as an image by multiplying the pre- dicted coefficients and the principal component images. Principal component images are already obtained in Section 2.2.1 by arranging the eigen vectors to two dimensional martrices. The three principal component images in case of whole 4DCT images are illustrated in Figure 3.
2.3. Quantification Using Cross Correlation Coefficient
In order to quantify the accuracy of the prediction algorithm the cross correlation coefficient was employed to
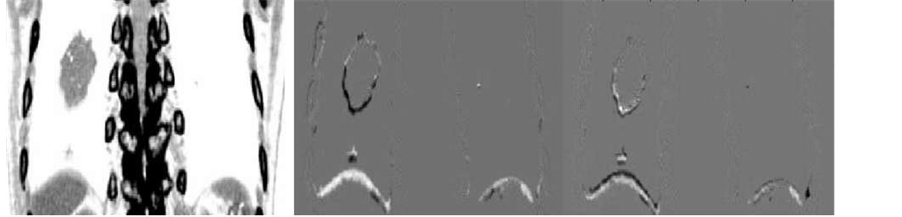
Figure 3. Three principal components for large view 4DCT images which are used for reformation of predicted images.
analyze the similarity between the original and the predicted images. In this study, the cross correlation coefficient was evaluated between the 10 sets of testing images and the predicted images in all the cases of image prediction (large view 4DCT prediction, ROI 4DCT prediction, markerless kV images and with marker kV images).
3. Results
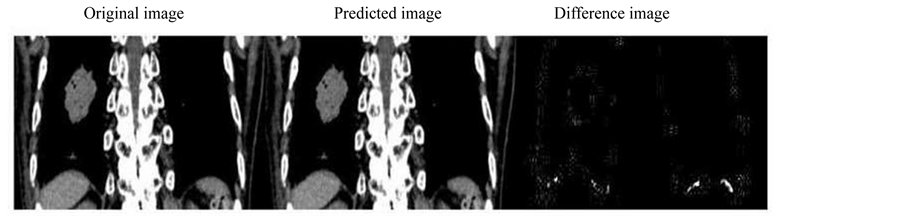
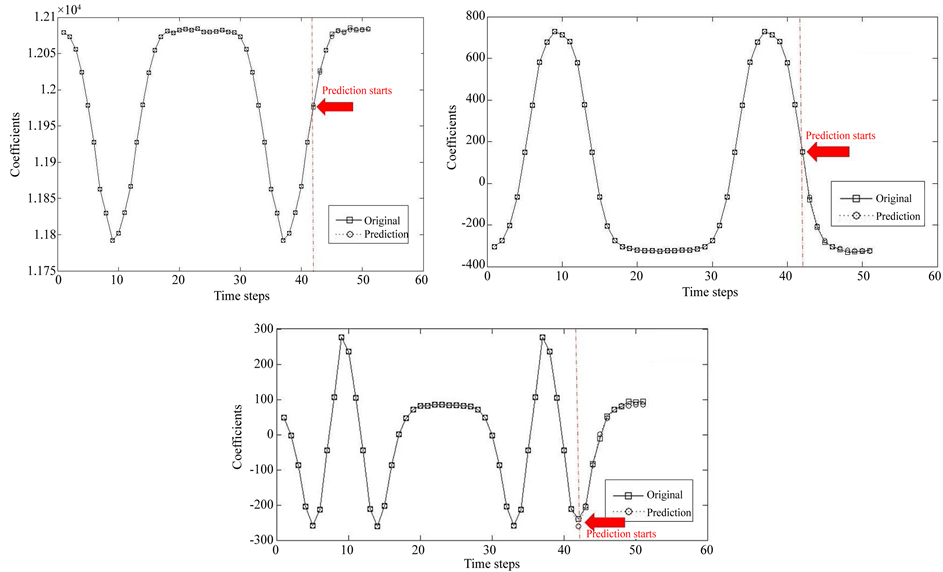
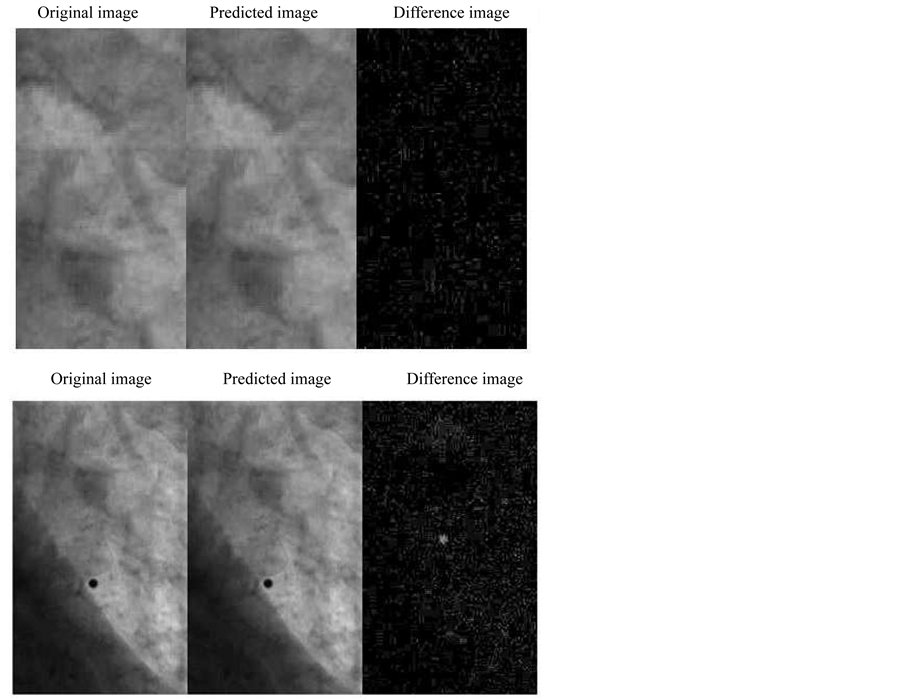
In 4DCT images, a few principal components were enough to represent the original feature of lung motion and deformation; Figure 3 shows the first three principal component images and the representative prediction image is shown in the middle panel of Figure 4 and Figure 5, where only three components were taken into account. One can see that the first principal component represents the entire feature of the body and the other components give a kind of corrections, especially, in the tumor surface and the diaphragm edge. As seen in Figure 4 and Figure 5, the difference from the original image is negligibly small, so that the prediction can be successfully obtained with only first three principal components. The corresponding coefficient values are indicated in Figure 6, where the prediction started after the 42nd step for the next ten steps. The predicted coefficient values are in agreement with the original ones. The evaluated image correlation was 0.9998 ± 0.0001 for large-view 4DCT, and 0.9992 ± 0.0002 for ROI 4DCT (Table 1). Although the value was slightly superior in large-view 4DCT, the calculation time was reasonably reduced in ROI 4DCT (0.6 sec ® 0.12 sec).
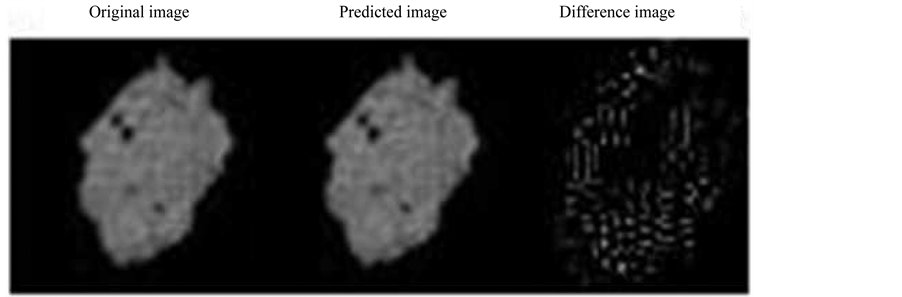
In contrast to 4DCT images, first twenty principal components had to be collected for the precise image prediction in kV fluoroscopic images. Figure 7 shows the prediction result for the kV fluoroscopic images including the tumor and tumor with marker, respectively. The quantitave anlaysis of the prediction result using cross correlation gave 0.9984 ± 0.0017 and 0.9957 ± 0.0030 with and without marker, respectively (Table 1).
The programming environment was MATLAB 2013A. The calculation time was less than 0.6 sec in all cases by using IntelCoreTM 2 Duo CPU P880 @ 2.66 GHz 4.00 GB RAM. For time improvement and comparison, calculation time is analysed using CPU Intel Xeon: E 31225 @ 3.10 GHz RAM: 4:00 GB which led to the improvement of the time by 3 times. The calculation time for each case is illustrated in Table 1.
4. Discussion
This study aims in the development of the prediction algorithm for the possible implementation in image guided lung cancer radiation therapy. To our best knowledge this is the first study which explores the possibility of dynamic tumor tracking with prediction based upon the images. The need of consideration of tumor deformation has been reported using active shape models [9] , however, it is yet far to be clinically implemented and hugely depends upon the breathing regularity, cardiac motion and a prior knowledge to the tumor shape. The clinically implemented Cyberknife system, the Varian RPM system and the Vero SBRT system includes markers or sur- face based tracking as an important criteria [13] . The potential benefits of our system over other these tumor tracking system includes 1) eliminating the need of implanted or surface markers and 2) ability to consider the deformation of tumor instead of only the motion or position. The phantom images described in Section 2.1.2 did not include the deformation of the tumor, however, from the patient 4DCT images shown in Section 2.1.1, it was demonstrated that the deformation of the shape of tumor can be successfully predicted in the present algorithm.
It should be noted that the parameter optimization plays a major role in this algorithm. In case of 4DCT
Figure 4. Image prediction result for large view 4DCT image which shows the original (left), predicted (center) and the difference image (right).
Figure 5. Image prediction result for ROI, the tumor and its anticipated moving range showing the original (left), predicted (center) and the difference image (right).
Figure 6. Result for the prediction of coefficient for the first principal component (left top), for the second principal component (right top), and for the third principal component (bottom centre).
Table 1. Cross correlation coefficient value and the calculation time for next ten image prediction of 4DCT and kV images.
Figure 7. Tumor only prediction (upper) and with marker prediction (bottom) for the kV fluoroscopic images.
images, three eigen vectors were enough to predict and reform. Further increase in the number of eign vectors did not have noticeable effects on the results. The reshaped eigen vectors (the principal component images) shown in Figure 3 show that the first principal component covers almost the whole feature of the input image followed by the second and third one after which it becomes minor components. However in the case of kV fluoroscopic images at least seven to ten eigen vectors were required to obtain the significant result. In the pre- sent study, we have taken into account the first twenty eigen vectors giving the best result. In this case, the actual tumor motion did not have such large cycle and amplitude. It was chosen in order to move the marker and the imitated tumor in various image background (lung, bone and heart), hence the ROI can be further reduced for the small amplitude which ultimately improves the calculating time.
Our input kV fluoroscopic images include both tumor and the marker. We have shown the prediction result including the marker (tumor and marker) and without the marker (only tumor). In both cases there is no much change in the correlation coefficient but there is significant reduction in time due to the reduction of the image size (smaller ROI) hence this method eliminates the use of considering markers. It can also be seen from the result in Figure 7 that due to characteristics of PCA the difference image is only the minor components that are not considered in the prediction.
In order to evaluate the accuracy of this algorithm the cross correlation has been calculated. This study is focused mainly upon the ability of tumor tracking with prediction with maximum accuracy and acceptable computing time rather than the computing time alone. This is because of the recent papers reporting the increasing computational power and the possible acceleration using a GPU-based computer [14] .
Since this dynamic tracking method is still in its preliminary stage we plan to test the accuracy of our algorithm in the kV projection images from the patients. In that case we can consider the deformation of the tumor and some real breathing pattern as in case of our 4DCT images in Section 2.1. Some artifacts and other physical effects are expected which will degrade the quality of image in the patient data. Some pre-processing such as noise removal or image enhancement might be necessary in those cases. We also need to evaluate this algorithm for the projection images in case of the treatment with rotating gantry such as a volumetric modulated arc therapy.
5. Summary
We have developed an algorithm using PCA and MSSA for the prediction of dynamic images of lung tumor during radiation therapy. We have used two different input images (4DCT and kV fluoroscopic images) for the validation of this algorithm. In kV images, we have also shown that including the marker shows no significant change in the prediction accuracy, while the calculation time is significantly reduced. The present result indicated that images were predicted with significant accuracy (more than 99% using correlation coefficient in each case). By using a high performance computer, the calculation time has been improved. Further improvements will be made by the application of the existing algorithm in the patient images acquired during treatment and doing the quantitative analysis for the reduction of target volume which is the ultimate goal of this research.
Acknowledgements
This research was partially supported by New Eenergy and Industrial Technology Development Organization (NEDO).
Cite this paper
Ritu BhusalChhatkuli,KazuyukiDemachi,NaokiMiyamoto,MitsuruUesaka,AkihiroHaga, (2015) Dynamic Image Prediction Using Principal Component and Multi-Channel Singular Spectral Analysis: A Feasibility Study. Open Journal of Medical Imaging,05,133-142. doi: 10.4236/ojmi.2015.53017
References
- 1. Cervino, L.I., Chao, A.K.Y., Sandhu, A. and Jiang, S.B. (2009) The Diaphragm as an Anatomic Surrogate for Lung Tumor Motion. Physics in Medicine and Biology, 54, 3529.
http://dx.doi.org/10.1088/0031-9155/54/11/017 - 2. Jiang, S.B. (2006) Technical Aspects of Image-Guided Respiration-Gated Radiation Therapy. Medical Dosimetry, 31, 141-151.
http://dx.doi.org/10.1016/j.meddos.2005.12.005 - 3. Shirato, H., Shimizu, S., Kunieda, T., Kitamura, K., van Herk, M., Kagei, K., Nishioka, T., Hashimoto, S., Fujita, K., Aoyama, H., et al. (2000) Physical Aspects of a Real-Time Tumor-Tracking System for Gated Radiotherapy. International Journal of Radiation Oncology*Biology*Physics, 48, 1187-1195.
http://dx.doi.org/10.1016/S0360-3016(00)00748-3 - 4. Cho, B., Poulsen, P.R. and Keall, P.J. (2010) Real-Time Tumor Tracking Using Sequential kv Imaging Combined with Respiratory Monitoring: A General Framework Applicable to Commonly Used IGRT Systems. Physics in Medicine and Biology, 55, 3299.
http://dx.doi.org/10.1088/0031-9155/55/12/003 - 5. Ma, L. (2007) Christian Herrmann, and Klaus Schilling. Modeling and Prediction of Lung Tumor Motion for Robotic Assisted Radiotherapy. IEEE/RSJ International Conference on Intelligent Robots and Systems, 29 October 2007-2 November 2007, 189-194.
- 6. Seppenwoolde, Y., Shirato, H., Kitamura, K., Shimizu, S., van Herk, M., Lebesque, J.V. and Miyasaka, K. (2002) Precise and Real-Time Measurement of 3d Tumor Motion in Lung Due to Breathing and Heartbeat, Measured during Radiotherapy. International Journal of Radiation Oncology*Biology*Physics, 53, 822-834.
http://dx.doi.org/10.1016/S0360-3016(02)02803-1 - 7. Isaksson, M., Jalden, J. and Murphy, M.J. (2005) On Using an Adaptive Neural Network to Predict Lung Tumor Motion during Respiration for Radiotherapy Applications. Medical Physics, 32, 3801-3809.
http://dx.doi.org/10.1118/1.2134958 - 8. Mukumoto, N., Nakamura, M., Yamada, M., Takahashi, K., Tanabe, H., Yano, S., Miyabe, Y., Ueki, N., Kaneko, S., Matsuo, Y., et al. (2014) Intrafractional Tracking Accuracy in Infrared Marker-Based Hybrid Dynamic Tumour- Tracking Irradiation with a Gimballed Linac. Radiotherapy and Oncology, 111, 301-305.
http://dx.doi.org/10.1016/j.radonc.2014.02.018 - 9. Xu, Q., Hamilton, R.J., Schowengerdt, R.A. and Jiang, S.B. (2007) A Deformable Lung Tumor Tracking Method in Fluoroscopic Video Using Active Shape Models: A Feasibility Study. Physics in Medicine and Biology, 52, 5277.
http://dx.doi.org/10.1088/0031-9155/52/17/012 - 10. Turk, M. and Pentland, A. (1991) Eigenfaces for Recognition. Journal of Cognitive Neuroscience, 3, 71-86.
http://dx.doi.org/10.1162/jocn.1991.3.1.71 - 11. Li, R., Jia, X., Lewis, J.H., Gu, X., Folkerts, M., Men, C. and Jiang, S.B. (2010) Real-Time Volumetric Image Reconstruction and 3d Tumor Localization Based on a Single X-Ray Projection Image for Lung Cancer Radiotherapy. Medical Physics, 37, 2822-2826.
http://dx.doi.org/10.1118/1.3426002 - 12. Mizuguchi, A., Demachi, K. and Uesaka, M. (2010) Establish of the Prediction System of Chest Skin Motion with SSA Method. International Journal of Applied Electromagnetics and Mechanics, 33, 1529-1533.
- 13. Ouzidane, M., Evans, J. and Djemil, T. (2014) Dedicated Linear Accelerators for Stereotactic Radiation Therapy. In: Benedict, S.H., Schlesinger, D.J., Goetsch, S.J. and Kavanagh, B.D., Eds., Sterotactic Radiosurgery and Stereotactic Body Radiation Therapy, CRC Press, Taylor and Francis Group, Boca Raton, 33487-2742.
- 14. Jia, X., Ziegenhein, P. and Jiang, S.B. (2014) GPU-Based High-Performance Computing for Radiation Therapy. Physics in Medicine and Biology, 59, R151.
http://dx.doi.org/10.1088/0031-9155/59/4/r151
NOTES
*Corresponding author.