Open Journal of Medical Imaging
Vol. 3 No. 1 (2013) , Article ID: 28545 , 14 pages DOI:10.4236/ojmi.2013.31004
On Wavelet Transform General Modulus Maxima Metric for Singularity Classification in Mammograms
1Department of Electrical Engineering & Computer Science, Syracuse University, Syracuse, USA
2Department of Electrical & Computer Engineering, Western Michigan University, Kalamazoo, USA
Email: tbujanov@syr.edu, ikhlas.abdelqader@wmich.edu
Received January 15, 2013; revised February 19, 2013; accepted February 28, 2013
Keywords: Continuous Wavelet Transform; Fractal Dimension; General Modulus Maximum; Microcalcification; Singularity; Smoothed Impulse Function
ABSTRACT
Continuous wavelet transform is employed to detect singularities in 2-D signals by tracking modulus maxima along maxima lines and particularly applied to microcalcification detection in mammograms. The microcalcifications are modeled as smoothed positive impulse functions. Other target property detection can be performed by adjusting its mathematical model. In this application, the general modulus maximum and its scale of each singular point are detected and statistically analyzed locally in its neighborhood. The diagnosed microcalcification cluster results are compared with health tissue results, showing that general modulus maxima can serve as a suspicious spot detection tool with the detection performance no significantly sensitive to the breast tissue background properties. Performed fractal analysis of selected singularities supports the statistical findings. It is important to select the suitable computation parametersthresholds of magnitude, argument and frequency range-in accordance to mathematical description of the target property as well as spatial and numerical resolution of the analyzed signal. The tests are performed on a set of images with empirically selected parameters for 200 μm/pixel spatial and 8 bits/pixel numerical resolution, appropriate for detection of the suspicious spots in a mammogram. The results show that the magnitude of a singularity general maximum can play a significant role in the detection of microcalcification, while zooming into a cluster in image finer spatial resolution both magnitude of general maximum and the spatial distribution of the selected set of singularities may lead to the breast abnormality characterization.
1. Introduction
Wavelet transform modulus maxima method was developed for detection and characterization of signal singularities by Mallat and his collaborators [1-3]. Their method detects signal singularities by tracking the wavelet coefficients magnitude maximum over scale. They proved that, if a wavelet function is derivative of a Gaussian, wavelet transform modulus maxima must propagate towards finer scales. Although the representation by discrete wavelet maxima is not complete since several signals may exhibit the same wavelet maxima [4], Mallat’s numerical experiments have shown that it is possible to reconstruct signals with a relatively small mean square error (smaller than 1%) [3].
Arneodo and his team focused on how to recognize a sharp signal transition by tracking its behavior over scale. Specifically algorithms based on continuous wavelet transform modulus maxima method are able to detect singular points in a discrete 2-D and 3-D signals and supported by fractal analysis to give the metrics for the local signal regularity [5-9]. Arneodo’s team developed fractal based algorithm [8] supported by modulus maxima method to analyze turbulent 2-D and 3-D signals.
Microcalcifications in breast are residual calcium deposits that originate not only from completely normal processes, but also abnormal ones. Shape, morphology, and spatial distribution of individual microcalcifications are some of the features detectable in X-ray mammograms that suggest benign or malignant breast abnormality. Researchers have made few breast tissue classifications and have recognized more than twenty of those conventional features [10-12]. One acceptable simplification is to describe microcalcifications as ellipsoids of diameters between 0.05 mm and 1 mm. For early cancer detection, calcifications with spatial extent less than 0.5 mm are most important for clinical diagnosis. Particularly, this corresponds to calcifications roughly in the order of 0.1 mm in diameter. Also, microcalcifications appearing in clusters may suggest malignancy while individual occurrences are of low clinical significance [13].
Wavelets as mathematical microscope have been used by many researchers in mammogram analysis. Wang and Karayiannis [14] proposed searching for microcalcifications by using high frequency energy blobs in wavelet decomposed mammograms. But normal signal fluctuation in mammograms may have dominant energy blobs in some scales making a mask over significant abnormality related information. Indeed, an energy blob is just a location where further analysis should follow. We use modulus maxima method to eliminate the singularities with positive Hölder exponent, because those singularities are present everywhere in mammograms (this is commented by fractal dimension of singularity spatial distribution in Section 4.4). In this work we show that the general modulus maximum, the largest magnitude value along a maxima line, and the scale in which it is detected are the most significant information to be used in further detection procedure. The argument of the detected general modulus maxima (the tangential directions of an edge around pixel) is another significant piece of information that is very useful in the target segmentation procedure (not discussed in this work).
Zhang and coworkers [15] studied the size of microcalcifications and developed an optimally weighted wavelet transform method by which, before image reconstruction, they multiplied dyadic wavelet coefficients by optimized coefficients 0.4, 1.6, 1.0, and 0.05 for the scales corresponding to 100 μm, 200 μm, 400 μm, and 800 μm respectively. They achieved Az = 0.92 under ROC curve, outperforming Az = 0.86 for difference-image technique.
Microcalcifications in mammogram analysis may be modeled as impulse functions smoothed by Gaussian filters. Strickland and Hahn [16] recognized Gaussian nature of microcalcifications spatial intensity and applied 2-D Gaussian filters for microcalcification detection. They inserted inter-scales to increase detection sensitivity for wide range of possible microcalcifications.
Since the Food and Drug Administration approved the technology in 1998, several Computer-Aided Detection (CAD) systems that support microcalcification detection have been deployed for clinical use. Literature reports show mixed results of current CAD systems in practice [17,18]. Results of some of the studies performed by using retrospective analyses or computer modeling suggested that CAD can achieve the main task increasing cancer detection.
Some studies show no practical improvements concluding that the CAD effect on the accuracy of interpretation is unclear [19] mostly because of radiologist’s false sense of confidence in CAD although in testing a CAD system applied to mammograms with known cancers might have excellent performance, known as “laboratory effect” [20].
This leads to a conclusion that different conditions of mammographic characteristics associated with X-ray exposure and breast tissue density should be studied across different institutions [21].
In this work, we consider microcalcifications as sharp signal transitions modeled as impulse functions smoothed by a Gaussian and characterized by negative Hölder exponent. We detect smoothed impulse functions and identify general modulus maxima and the scales in which they appear. Essentially detected general maxima show the scale in which the singularities are visible as the step functions with Hölder exponent approaching to zero. If in the higher scales the magnitude of the wavelet coefficients starts decreasing the singularity shows its impulse nature. Figure 1 illustrates the modulus maxima behavior over scale for the singularities with and without impulse nature, i.e. microcalcification and normal breast tissue signal fluctuation. The magnitude of modulus maxima of normal breast tissue signal fluctuation can become dominant (higher energy in higher scales) and affect the detection of the singularity with impulse nature (lower energy in higher scales) which represents a microcalcification in this case.
We detect the wavelet coefficient magnitude in the scale in which a singularity behaves as a step function and in higher scales becomes negative showing impulse nature of the singularity. Notice that normal breast tissue exhibits local signal fluctuation with many smoothed impulse functions in mammograms. This requires that in the next step detected smoothed impulse functions should be classified as significant for further analysis if they have locally dominant magnitudes of general maxima. In short, we take advantage of the capabilities of continuous wavelet transform modulus maxima method to detect signal singularities and differentiate between microcalcifications and normal signal fluctuation keeping track how Hölder exponent is developing over scale.
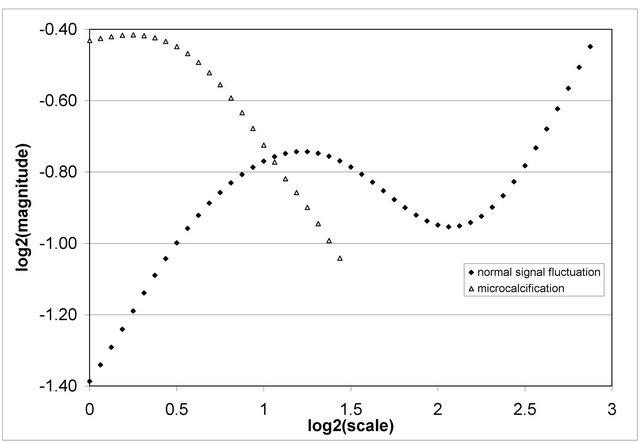
Figure 1. Typical log-log characteristics Modulus Maxima vs scale for a normal signal fluctuation (¨) and a microcalcification (Δ) in the mammogram mdb226 [22].
After detection in coarser spatial resolution, based on the fact that this method can detect step function, a cluster of singularities could be segmented in finer resolutions with appropriately adjusted settings. This method could be used for singularity border transition analysis i.e. its shape analysis for diagnostic purposes and therefore microcalcification estimation malignant vs benign [12].
In this work we demonstrate use of general maxima metric in mammograms with 200 μm/pixel spatial and 8 bits/pixel numerical resolution to speed up detection not of microcalcification border, but microcalcification itself. The scale of the general maxima detection depends on the size of the singularity and since singularity size in mammograms differs from one to another there is no typical scale but scale distribution that could be identified.
The magnitudes and their spatial distribution are analyzed in 25 regions containing microcalcification clusters from diagnosed 20 mammograms and the results compared to the results of 20 regions with healthy tissue from the same mammograms [22]. Additionally, we recognize and select smoothed impulse function by its negative Hölder exponent. Detection of a magnitude of a general maximum doesn’t depend on the negative slope value within the detection procedure. This makes general modulus maximum stronger and more independent feature i.e. that is an excellent candidate to integrate with other features.
Background on the continuous wavelet transform, modulus maxima method, and fractal dimensions are presented in Section 2. In Section 3 we present the details of the framework and its implementation. The results from both statistical and fractal implementations, including the samples of tested mammograms, are presented in Section 4 while Conclusions are presented in Section 5.
2. Background
The presence of strong local singularities is characterized by negative Hölder exponent while normal fluctuation is mostly characterized by positive Hölder exponent. This makes an isolated singularity detectable by analyzing the behavior of a modulus maximum along its maxima line.
Mallat and Hwang [1] proved that the magnitudes of the wavelet coefficients are bounded as shown in (1):
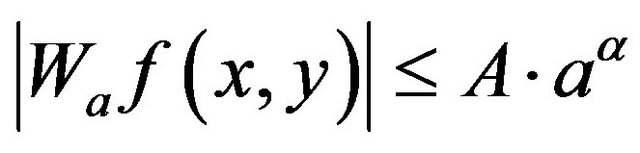 (1)
(1)
where 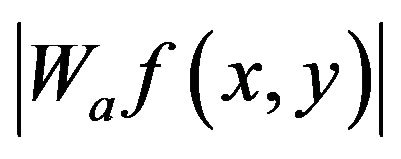 is magnitude of the wavelet coefficient at point (x, y) in scale a, a is Hölder exponent at (x, y) and A > 0 is a constant.
is magnitude of the wavelet coefficient at point (x, y) in scale a, a is Hölder exponent at (x, y) and A > 0 is a constant.
When Hölder exponent at (x, y) is positive the magnitude of wavelet coefficient will increase with scale while when it is negative, as in case of impulse function, the magnitude of the wavelet coefficient will decrease. Mathematically local microcalcification of the mammogram signal may be modeled as an impulse function convolved by a Gaussian smoothing function.
For further analysis of behavior of magnitude of wavelet coefficients in scale, we use a wavelet coefficient magnitude approximation [3]
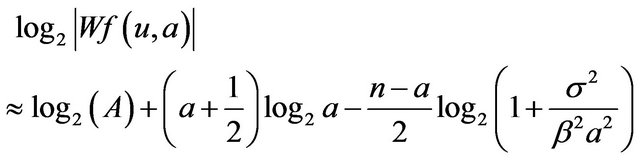 (2)
(2)
where a targeted microcalcification is modeled as an impulse function smoothed by Gaussian of variance σ2 and convolved by a Gaussian wavelet with variance β2.
If a tends to −1, then the magnitude of a wavelet coefficient increases up to the scale corresponding to the variance s2 reaching wavelet transform general modulus maximum followed by a decrease as in the case of microcalcification shown in Figure 1. An example of normal signal fluctuation generally characterized by positive Hölder exponent in the scales having increasing magnitude of wavelet coefficients is also shown in Figure 1.
2.1. Modulus Maxima Representation
A Gaussian smoothing function at scale a
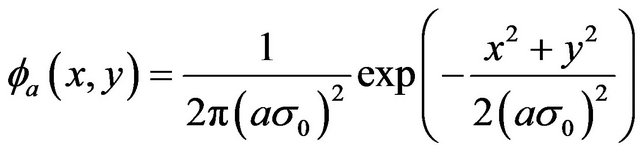 (3)
(3)
has been used as a kernel for wavelet transform discrete filters. The horizontal and vertical wavelet coefficients at scale a are defined as
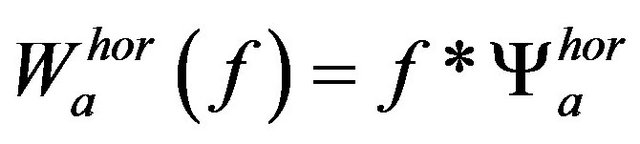 (4)
(4)
and
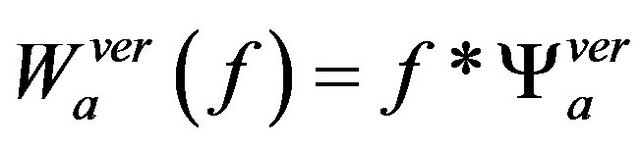 (5)
(5)
respectively, where the horizontal and vertical wavelets 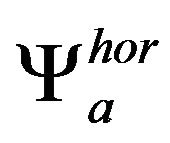 and
and 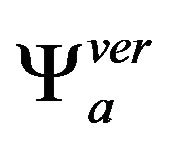 in scale a are derivatives of smoothing function fa in the same scale a
in scale a are derivatives of smoothing function fa in the same scale a
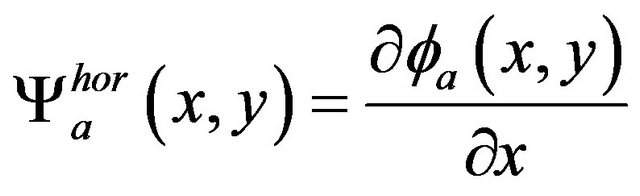 (6)
(6)
and
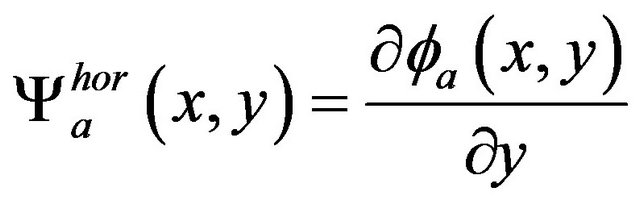 (7)
(7)
respectively.
Wavelet coefficient at a scale a is represented by its magnitude and argument as follows,
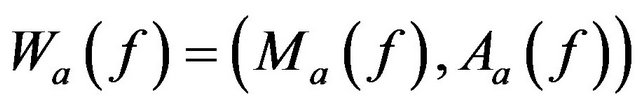 (8)
(8)
where 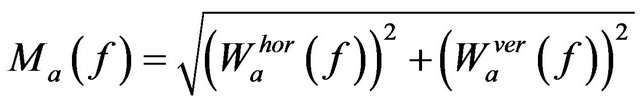 and
and
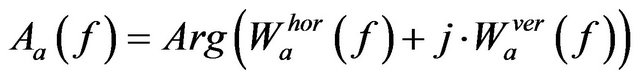 , with horizontal and vertical wavelet coefficients
, with horizontal and vertical wavelet coefficients 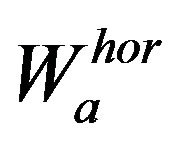 and
and 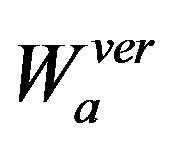 at scale a, defined in (4) and (5) respectively.
at scale a, defined in (4) and (5) respectively.
A modulus maximum at (x0,y0) at the scale a is represented by its magnitude if it is equal or greater than wavelet coefficient magnitude in its neighborhood. There is no detected modulus maximum at (x0,y0) in scale a if any surrounding wavelet coefficient magnitude is grater than magnitude at (x0,y0), i.e.
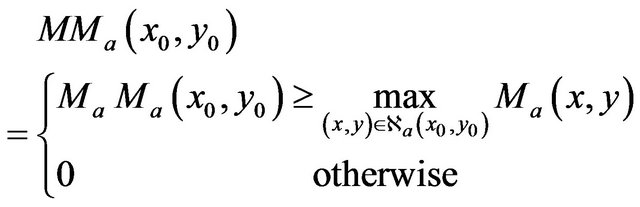 (9)
(9)
where 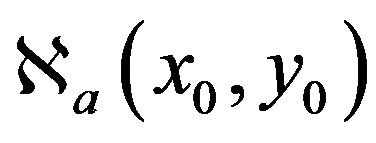 is 8-neighborhood of (x0,y0) in the scale a.
is 8-neighborhood of (x0,y0) in the scale a.
While a maxima line consists of the wavelet transform modulus maxima corresponding to the same local feature but in different scales, the general modulus maximum is a point on the maxima line characterized by its maximal magnitude 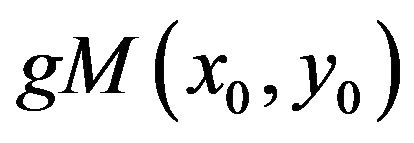 and the scale
and the scale 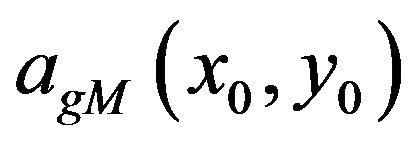 in which it is detected. Wavelet transform general modulus maximum will appear with a magnitude and in a scale that depends on the initial variance of the smoothing Gaussian in the initial scale a0 = 1.
in which it is detected. Wavelet transform general modulus maximum will appear with a magnitude and in a scale that depends on the initial variance of the smoothing Gaussian in the initial scale a0 = 1.
In the higher scales of 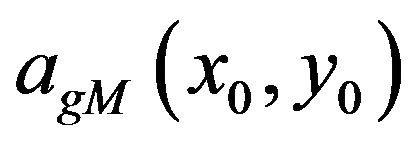 corresponding maxima line will exist as long as the smoothed impulse function is the dominant singularity in its neighborhood. In that range the slope of the log-log diagram modulus maxima vs scale will tend to −1 if the maxima line is long enough, i.e. until it is overlapped by a modulus maximum of another dominant singularity. If in higher scales the singularity stops being dominant in its neighborhood, the maxima line tracking process should be interrupted to prevent misleading singularity detection. The magnitude
corresponding maxima line will exist as long as the smoothed impulse function is the dominant singularity in its neighborhood. In that range the slope of the log-log diagram modulus maxima vs scale will tend to −1 if the maxima line is long enough, i.e. until it is overlapped by a modulus maximum of another dominant singularity. If in higher scales the singularity stops being dominant in its neighborhood, the maxima line tracking process should be interrupted to prevent misleading singularity detection. The magnitude 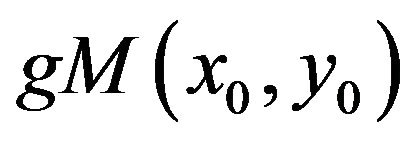 and the scale
and the scale 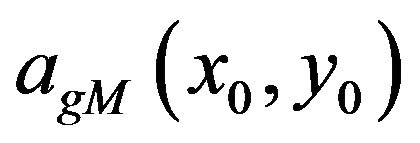 in which the general modulus maximum is detected as well as the length of maxima line afterward are significant starting points for evaluating the isolated singularities.
in which the general modulus maximum is detected as well as the length of maxima line afterward are significant starting points for evaluating the isolated singularities.
2.2. Fractals, Partition Function and Dimension
A fractal is an object or quantity that displays self-similarity in all scales. A plot of the quantity on a log-log graph versus scale then gives a straight line, which slope is said to be the fractal dimension. The prototypical example for a fractal is the length of a coastline measured with different length ruler. The shorter the ruler, the larger the length measured, a paradox known as the coastline paradox or “the Richardson effect” (L. F. Richardson, 1881-1953) [23].
Fractal dimension or capacity dimension of a fractal is the exponent D in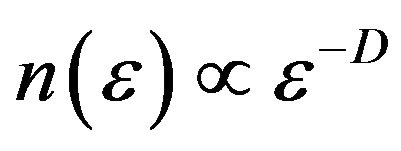 , where
, where 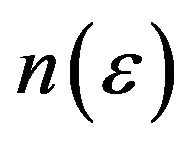 is the minimal number of balls of diameter e needed to cover the fractal set in each scale. Wavelets provide a natural generalization of the classical box-counting techniques to fractal signals, i.e. the wavelets are playing the role of generalized boxes. The wavelet transform as a mathematical microscope can be used to extract microscopic information about scaling properties of fractal objects [6]. Partition function can be derived from maxima line skeleton as
is the minimal number of balls of diameter e needed to cover the fractal set in each scale. Wavelets provide a natural generalization of the classical box-counting techniques to fractal signals, i.e. the wavelets are playing the role of generalized boxes. The wavelet transform as a mathematical microscope can be used to extract microscopic information about scaling properties of fractal objects [6]. Partition function can be derived from maxima line skeleton as
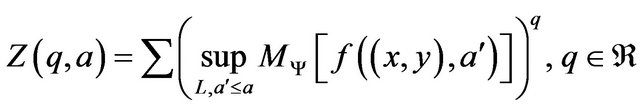 (10)
(10)
The analogy related to multifractal formalism in thermodynamics allows the following definition of the exponent t(q) for the behavior of partition function along the scale:
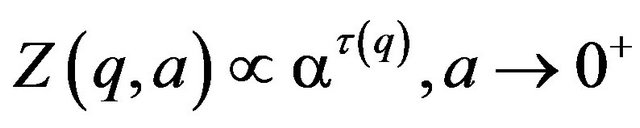 (11)
(11)
where q and t(q) represent inverse temperature and free energy in statistical mechanics. For homogenous fractal functions-monofractals and q = 0, the value of −t(q) is associated to fractal dimension of the set of all selected singularities [7].
According to (11), fractal dimension of a selected set of singularities is determined as the negative value of the slope of log-log characteristics of partition function Z(q,a) vs scale a with q = 0 as shown in Section 4.
3. Framework
In our experiments the targets are the microcalcifications sized from 0.2 mm to 1 mm in diameters. Accordingly to the mammogram spatial resolution, the scale is changing in three octaves. Notice that algorithm parameters, such as initial smoothing function variance and length of maxima lines necessary for the target detection, depend on the mammogram spatial resolution and the size of expected targets. Also, the general modulus maxima analysis can be used in 1-D and 3-D signals in a similar fashion.
Changing the scale, Gaussian filters are used to compute wavelet transform coefficients of mammographic images in vertical and horizontal direction in three octaves. The framework is based on using wavelet transform modulus maxima to identify the maxima lines in a mammogram and then extract the general modulus maximum on each maxima line. Also in each maxima line a corresponding minimum is detected in higher scales than general maximum and before maxima line fades out. Singularities pointed by maxima lines with no identified corresponding minimums are considered as normal signal fluctuation and rejected from further analysis. Singularities with detected corresponding minimums have negative Hölder exponents. The fact that described general maximum and corresponding minimum are clearly detected means the log-log characteristic modulus maxima vs scale has negative slope and isolated smoothed impulse function is localized at the point where maxima line propagates to scale a = 1. A maxima line might not propagate to a single point at scale a = 1 because of fast oscillations in the cone of influence around terminal point of the maxima line in the lowest detected scale [3]. This location will be classified as an eligible singularity if the general maximum and corresponding minimum is detected.
An illustration of applied framework is shown in Figure 2.
Can we fix that now? Should we reformat the entire text to avoid empty (blank) space or they would do it?
Variance of smoothed impulse function can be estimated by the scale in which general maximum is detected [24]. The selection of wavelet coefficients depends on the description of the singular point that we are detecting. In mammogram signals, we are adjusting the scale to the expected size of the microcalcification (50 μm to 1 mm) and the input spatial resolution of the mammogram (usually 50 μm). If both the general maximum and corresponding don’t exist on a maxima line its detected singularity is classified as normal signal fluctuation, i.e. the maxima line is not related to a microcalcification. A microcalcification boundary can be detected in the scales that correspond to 50 mm to 100 mm, i.e. the microcalcification segmentation needs additional information from finer image spatial resolution and it was not part of these experiments. Notice that, for example, the shape [12] of the targeted singularity can be involved in further singularity sub-classification.
Gaussian kernels and their derivatives are used to enable image processing with no particular bias in the spacescale analysis. Significant fractal properties can change very fast in scale. They often become invisible within less than a 1/2 of an octave and with coarse scale increment the trend of modulus maxima behavior in scale could not be detected.
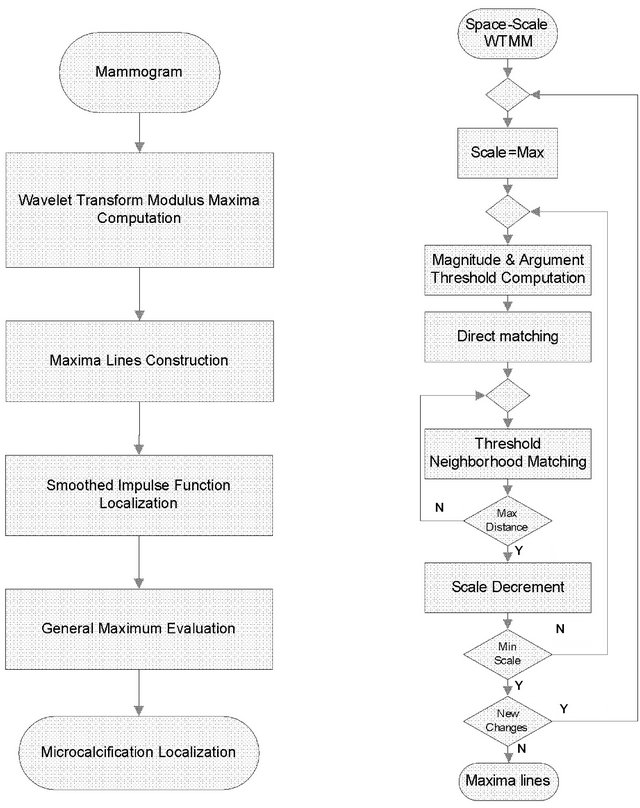 (a) (b)
(a) (b)
Figure 2. General Maximum detection and microcalcification localization block diagram (a) and maxima line construction block diagram (b).
Each maxima line points to a singularity and each singularity is analyzed based on the modulus maxima behavior along its maxima line.
Detected singularities gradually change in scale both the magnitude M and the argument q of their modulus maxima. Two maxima points in two consecutive scale layers belong to same maxima line if their spatial locations and their arguments are similar. The level of similarity of spatial distance and argument difference are below empirically determined thresholds. The experiments show that the detection process converges if the scale increment between two consecutive scale layers is as low as inc = 21/16. Then the algorithm will properly form a maxima line with the argument threshold dA = p × log2(inc)/4 radians or Dq < dA = p/64 radians in the simulations presented in Section 4.
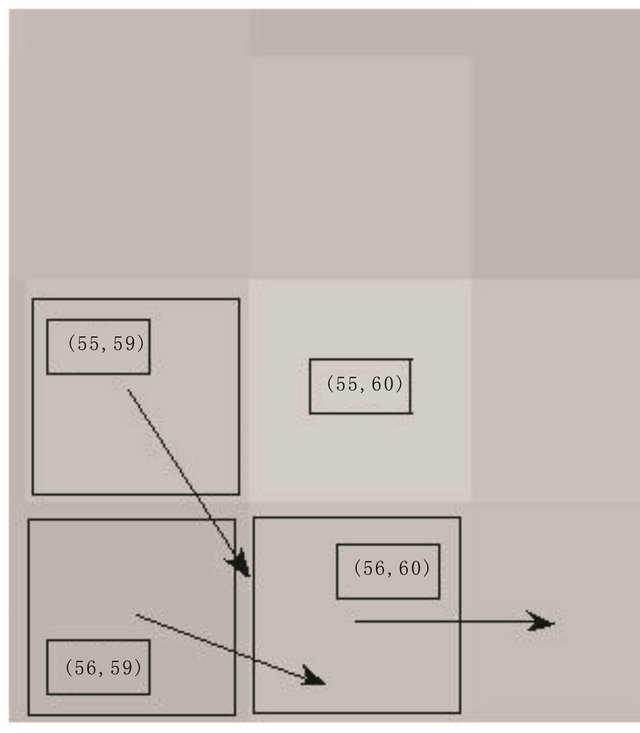
In some specific situations when maxima line switches from one point to another and both are the parts of the same feature, the argument difference can be significantly larger than the argument threshold and then magnitude threshold will be checked as an alternative to the argument threshold. The magnitude threshold applied in the simulations presented in this work was adaptive in both space and frequency domain, i.e. the threshold was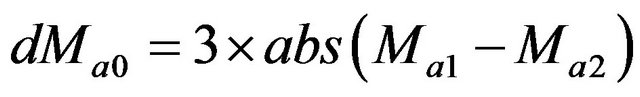 , where Ma1 and Ma2 are the modulus maxima detected in two higher consecutive scales. An example of described situation is presented in Figure 3.
, where Ma1 and Ma2 are the modulus maxima detected in two higher consecutive scales. An example of described situation is presented in Figure 3.
With the parameter setup applied in this work we consider 1/4 of an octave a minimum scale distance between general modulus maximum and corresponding minimum to classify a location as an eligible singularity.
4. Results and Discussion
The mammograms from database [22] are digitized at 50 μm pixel edge and reduced to spatial resolution 200 μm pixel edge and clipped/padded so that every image is 1024 × 1024 pixels. The area of a pixel represents 0.04 mm2 of breast tissue. Numerical resolution is 8 bits/pixel. In this work 12 malignant and 13 benign microcalcification clusters detected in 20 mammograms along with other 20 healthy regions selected from the same mammograms are used.
We find that normal and noise related detected eligible singularities are represented with significantly lower general modulus maxima comparing to those related to diagnosed microcalcification. We have introduced spatially local adaptive threshold in magnitude, to suppress false positive findings. The magnitudes above the local threshold we name (locally) dominant magnitude.
In this work we study magnitude and spatial distribution of general maxima of three different sets of detected singularities in the 64 × 64 pixel sub-images of the diagnosed 25 microcalcification clusters:
1) All detected singularities which show negative
 (a)
(a)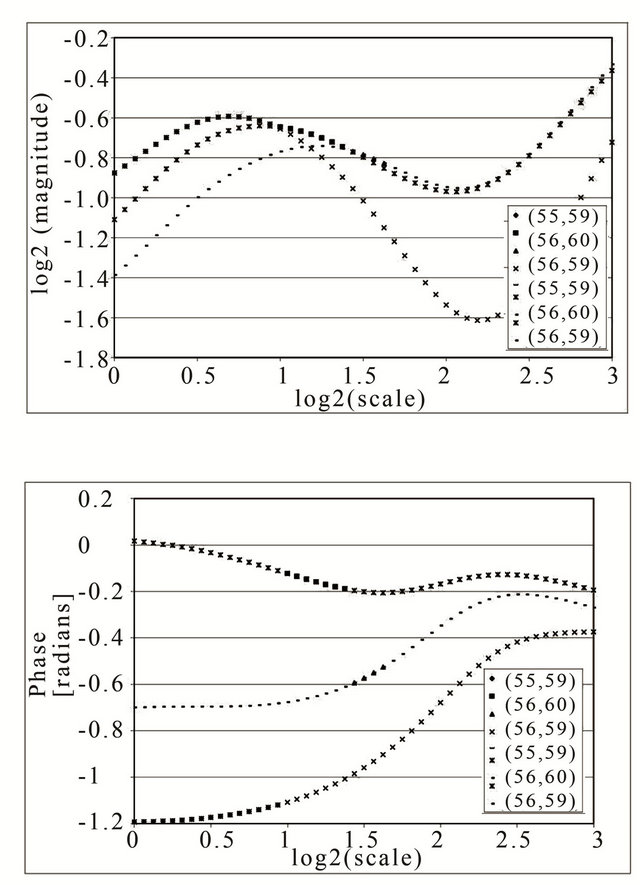 (b)
(b)
Figure 3. Example of maxima line construction from three singular points that belong to same sharp transition: Three singular points around the pixel (55, 60), (a), that can compose a maxima line as shown in bold and colored symbols in (b-up). Their arguments are significantly different representing the tangential directions of an edge around pixel (55, 60) but in higher scales they converge to the same limit as clearly illustrated in (b-down). Bolder symbols in the diagrams represent the values that belong to detected maxima line representing the same higher scale structure.
Hölder exponent resembling smoothed impulse function2) The subsets of the set selected in 1, with dominant magnitudes of computed general maxima resembling microcalcifications, and 3) The sets of singularities that correspond to the diagnosed microcalcifications in 25 clusters.
Assuming that the nature of malignant and benign microcalcification clusters is different we additionally study each category described above separately as malignant and benign abnormality.
In addition we study magnitude and spatial distribution of general maxima of three different sets of detected singularities in 20 healthy areas of same mammograms:
1) All detected singularities which show negative Hölder exponent and resembling smoothed impulse function in healthy areas, and 2) The subsets of 1 that have dominant magnitudes of computed general maxima in health areas.
Finally, we compare our results with respect to the background breast tissue type: dense (D), glandular (G), and fatty (F) tissue.
4.1. Differentiation Normal vs Abnormal Singularities
In 25 microcalcification clusters our method detected total of 3115 eligible maxima lines. The histogram of eligible general maxima magnitudes is shown in Figure 4- blue line. The histogram of general maxima gM related to the diagnosed microcalcification findings is red line in Figure 4.
For the comparison, the histograms of the detection of eligible general maxima magnitudes in 20 healthy areas
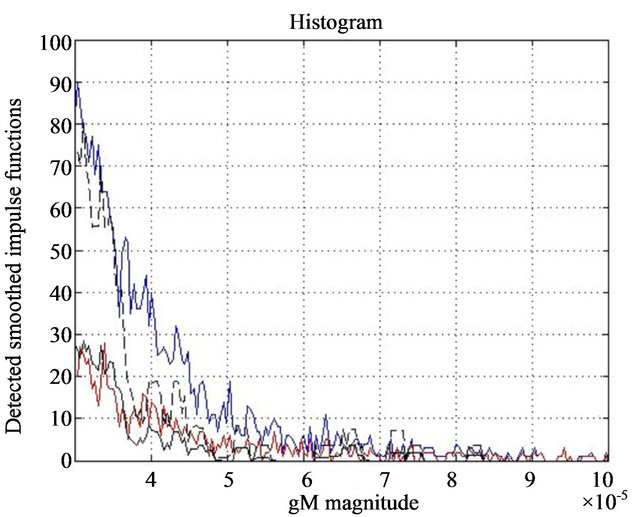
Figure 4. Histogram of total eligible findings in the areas of diagnosed clusters-blue line, and diagnosed microcalcifications in 25 clusters-red line. Histogram of total singularity findings in 20 healthy areas-black dashed line, and the eligible findings with a local intensity maximum in their neighborhood in same 20 healthy areas-black line.
is determined and presented as a dashed black line in Figure 4, while the black line in the same diagram is the histogram of detected eligible general modulus maxima magnitudes with associated local intensity maximums in the neighborhood.
For the purpose of further analysis of the diagrams in Figure 4 we introduce diagnosed rate function 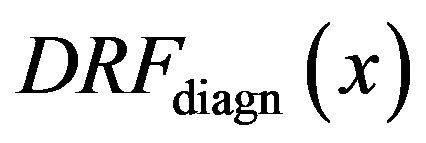 for the diagnosed microcalcifications by
for the diagnosed microcalcifications by
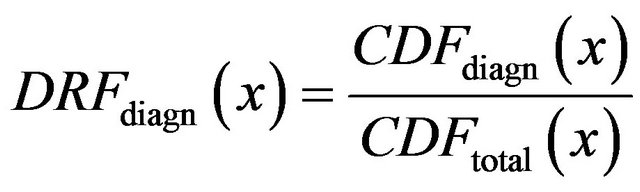 (12)
(12)
where x is general maxima magnitude,
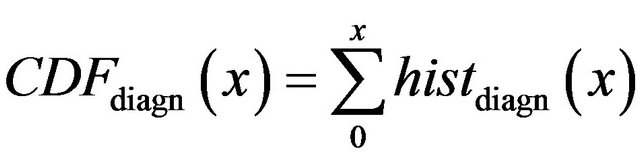 is cumulative distribution function of general maxima for diagnosed microcalcifications (red line) and
is cumulative distribution function of general maxima for diagnosed microcalcifications (red line) and 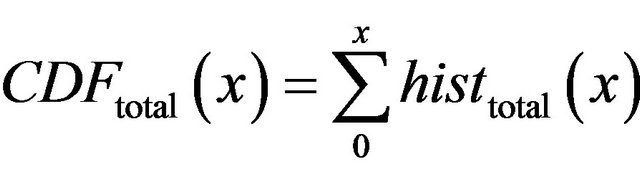 is cumulative distribution function of general maxima for total eligible general modulus maxima (blue line) both in [0, x].
is cumulative distribution function of general maxima for total eligible general modulus maxima (blue line) both in [0, x].
While an impulse may be negative, a microcalcification is, in general, a spot brighter than its surroundings. Similarly to the function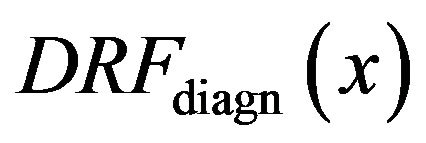 , here we institute the function
, here we institute the function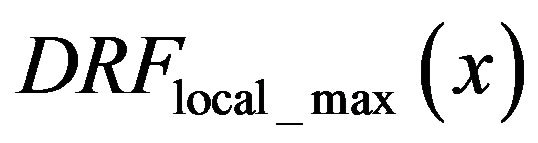 , the ratio of detected impulses with the local intensity maximums in their neighborhood and total detected smoothed impulse functions. i.e.
, the ratio of detected impulses with the local intensity maximums in their neighborhood and total detected smoothed impulse functions. i.e.
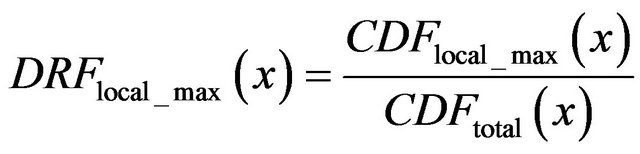 (13)
(13)
where x is general maxima, magnitude,
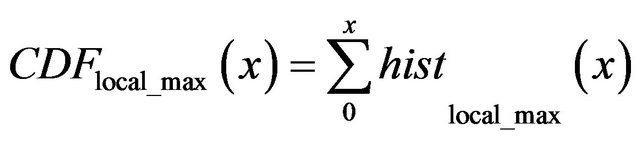 is cumulative distribution function of general maxima for smoothed impulses with detected local maximum in each of their neighborhood (red line) and
is cumulative distribution function of general maxima for smoothed impulses with detected local maximum in each of their neighborhood (red line) and
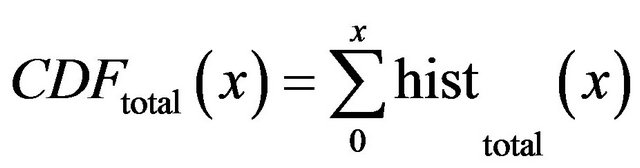 is cumulative distribution function of general maxima for total eligible general modulus maxima (blue line).
is cumulative distribution function of general maxima for total eligible general modulus maxima (blue line).
In the same set of 20 mammograms we also choose 20 healthy areas and select all singularities that could be modeled as smoothed impulse function. The histogram of the total number of selected singularities vs gM magnitude is shown as dashed black line in Figure 4. Assuming that a microcalcification is presented in mammograms as a spot brighter than its neighborhood we select a sub-set of all singularities in which neighborhood a local intensity maximum is detected. The histogram of the singularities in the sub-set vs gM magnitude is shown as black line in Figure 4.
The diagram of the function 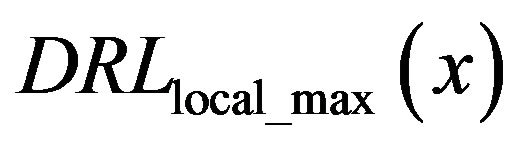 in the set of analyzed sub-images with diagnosed microcalcification clusters is the black line in Figure 5, while the dashed black line in Figure 5 represents same function
in the set of analyzed sub-images with diagnosed microcalcification clusters is the black line in Figure 5, while the dashed black line in Figure 5 represents same function 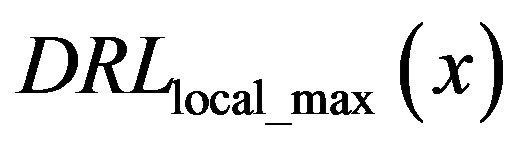 but in the set of analyzed sub-images without diagnosed microcalcifications.
but in the set of analyzed sub-images without diagnosed microcalcifications.
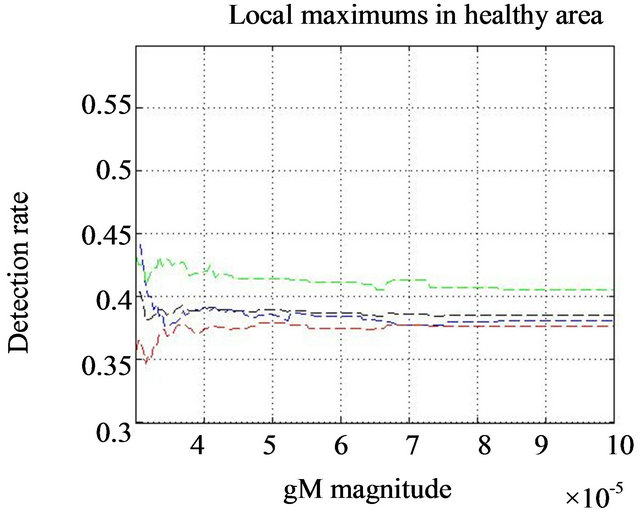
For each line in Figure 5 we notice two segments: an increasing, say non-linear, part on the left-hand side and an approximately linear behavior of each line on the right hand side. Numerically, we notice that linearity of dashed black line (having negative slope) starts between 3 × 10−5 and 4 × 10−5 in the case of healthy tissue samples, while in the case of diagnosed abnormalities for both lines the linearity (red and full black lines (having positive slope) starts above 4 × 10−5.
To confirm this observation about positive and negative slope we performed same experiment separating the results for dense (D), glandular (G), and fatty (F) tissue. In Figure 6 the diagnosed rate functions 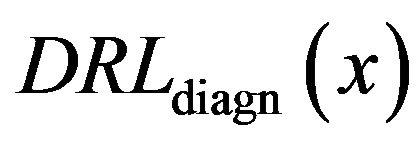 are presented as full colored lines: blue-glandular, reddense, and green-fatty background tissue. All three background tissue based full lines have increasing linear parts on the right hand side. The detection rate functions
are presented as full colored lines: blue-glandular, reddense, and green-fatty background tissue. All three background tissue based full lines have increasing linear parts on the right hand side. The detection rate functions 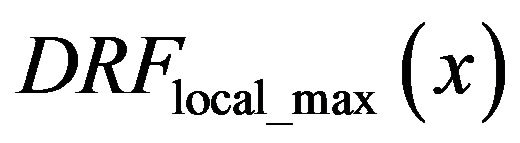 of smoothed impulse functions with local intensity maximums in the neighborhood is shown as dashed lines with same color schedule. All three dashed lines based on healthy tissue have decreasing linearity on the right hand side.
of smoothed impulse functions with local intensity maximums in the neighborhood is shown as dashed lines with same color schedule. All three dashed lines based on healthy tissue have decreasing linearity on the right hand side.
In same experiment we notice the difference in behavior of the function 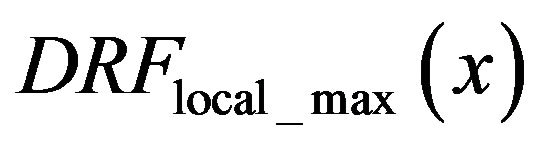 in the normal subimages (no microcalcifications-Figure 7(a) and in the subimage with diagnosed microcalcification clusters-Figure 7(b).
in the normal subimages (no microcalcifications-Figure 7(a) and in the subimage with diagnosed microcalcification clusters-Figure 7(b).
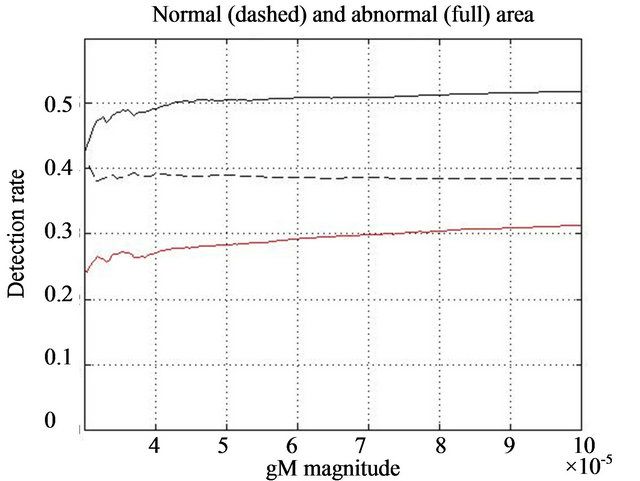
Figure 5. Diagnosed rate function 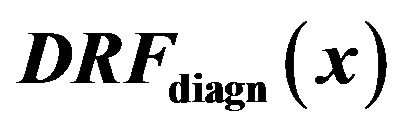 red line, detection rate of eligible singularities assiciated with a local intensity maximum in the neghborhood in the clusters
red line, detection rate of eligible singularities assiciated with a local intensity maximum in the neghborhood in the clusters 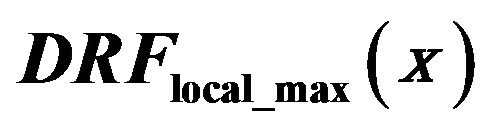 full black line, and
full black line, and 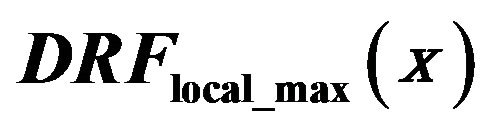 in healthy tissue dashed black line.
in healthy tissue dashed black line.
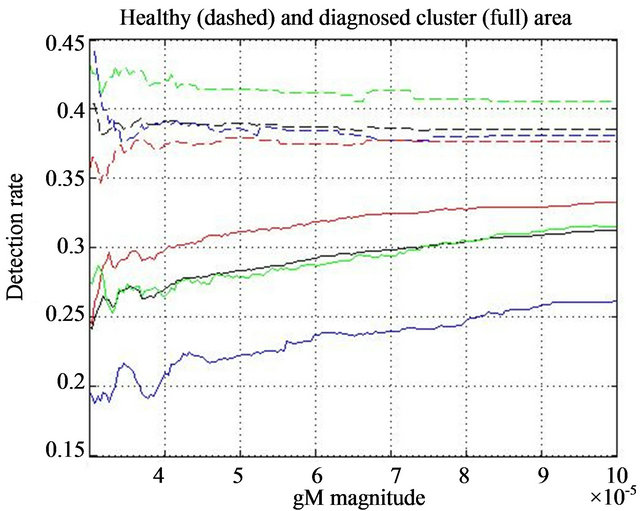
Figure 6. Smoothed impulse function detection rate comparison for diagnozed microcalcification clusters 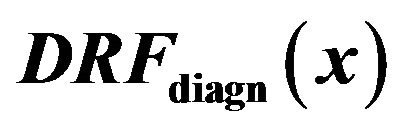 (full lines) and for corresponding healthy tissue
(full lines) and for corresponding healthy tissue 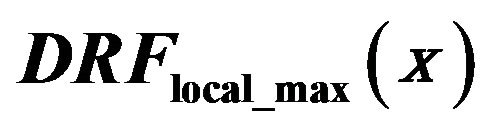 (dashed lines). Black lines show the behavior of detection rate vs general maxima magnitude for all tested clusters, while blue, red, and green lines are related to glandular, dense, and fatty tissue, respectively.
(dashed lines). Black lines show the behavior of detection rate vs general maxima magnitude for all tested clusters, while blue, red, and green lines are related to glandular, dense, and fatty tissue, respectively.
We conclude that positive vs. negative slope of the linear parts on the right hand side leads to a good differentiation between abnormal and normal tissue sample. We notice that the average magnitude of the general modulus maxima in 25 clusters is 4.18 × 10−5, while in 20 healthy background sample is 3.59 × 10−5. Both averages are in the range of gM magnitude that could be considered in either non-linear or linear part of corresponding lines. This leads to another conclusion that a successful differentiation normal vs. abnormal findings could be expected when an adaptive threshold is set to the local average of gM magnitudes.
For the abnormalities below the local averages the additional microcalcification features should be considered.
4.2. Threshold
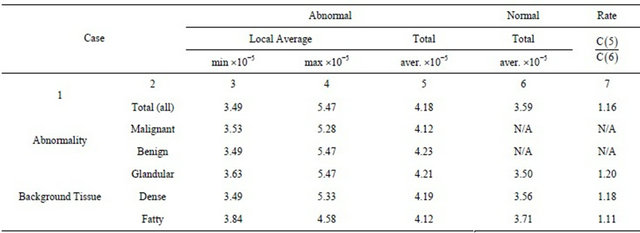
In tested 25 clusters of microcalcifications we found 3115 eligible maxima lines that point to smoothed impulses. For each cluster centered in a 64 × 64 pixel subimage we calculated average general modulus maxima magnitude. The results of the calculation of general modulus maxima averages are shown in Table 1.
The local and total averages, presented in Table 1, are used to estimate capabilities of the applied method for the microcalcification detection. The average magnitude of general maxima of all detected eligible smoothed impulse functions in healthy areas was 3.59 × 10−5 (Table 1, Total-Column 6), while the average magnitude in areas with diagnosed microcalcification clusters was 4.18 × 10−5 (Table 1, Total-Column 5), which is 16% increase
Table 1. Local and total gM magnitude averages in breast tissue with abnormal and normal findings.
 (a)
(a)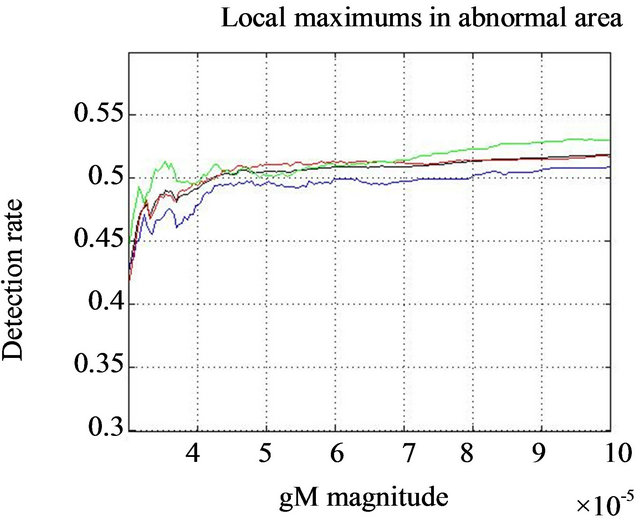 (b)
(b)
Figure 7. Smoothed impulse function with local intensity maximum in its neighborhood detection rate 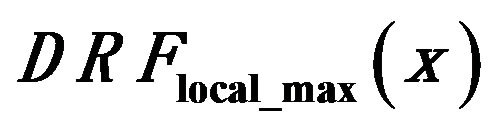 comparison for healthy tissue dashed lines (a) and the regions consisting diagnozed microcalcification clusters full lines (b). Black lines show the behavior of detection rate vs gM magnitude for all tested clusters, while blue, red, and green lines are related to glandular, dense, and fatty tissue, respectively.
comparison for healthy tissue dashed lines (a) and the regions consisting diagnozed microcalcification clusters full lines (b). Black lines show the behavior of detection rate vs gM magnitude for all tested clusters, while blue, red, and green lines are related to glandular, dense, and fatty tissue, respectively.
(Table 1, Total-Column 7). Similarly, the increase exists in each tested background tissue (20%, 18%, and 11% in the case of glandular, dense and fatty tissue, respectively) showing that microcalcification detection based on this feature is not qualitatively sensitive on background tissue.
The minimal computed average magnitude in an abnormal dense area was 3.49 × 10−5 (Table 1, Dense-Column 3), which was lower than corresponding average in normal dense areas 3.56 × 10−5 (Table 1, Dense-Column 6), showing that hard absolute thresholding (for example at 3.50 × 10−5) would not result in proper classification. Although the microcalcification related additional criterions would help the proper classification, in this analysis we evaluate the magnitude of general maxima in microcalcification detection leaving the combination of criterions for further research.
As we said, the averages in Column 5 and Column 6 in Table 1 could be considered in both linear and non-linear part of the diagrams presented in Figures 5-7. We conclude that a threshold based on the local average of gM magnitude will yield an appropriate classification of singular points. Further lowering the threshold would cause more false positive findings and therefore requires the additional classification criterions, while higher threshold would decrease classification sensitivity.
4.3. Statistical Analysis of Singularities in Breast Tissue
In following analysis, a magnitude threshold of the general modulus maxima was determined as the local average of all gM magnitudes of all eligible maxima lines with detected negative Hölder exponent in the area 64 × 64 pixels centered in a diagnosed cluster. This choice of the adaptive threshold has reduced the number of dominant singularities down to 970 (31.1%) of all 3115 eligible singularities (Table 2, Total, Column 4), while 1179 (37.8%) were pointing either malignant or benign microcalcifications. The true positive fraction (sensitivity) was 65.2%, which results in ROC curve area index Az = 0.77.
In the case of the malignant microcalcifications we find 33.3% as suspicious, while the malignant microcalcifications were 48.7%, meaning that the average threshold is too high. In Table 3 we see that only 2% were false positive against 17.5% false negative findings. True positive fraction was 64.1%, while ROC curve area index was Az = 0.80.
We find a different tendency in the case of benign microcalcification. The average threshold classified 29.1%, while benign microcalcifications were 27.3%, meaning that the average threshold was set a little lower than optimal. False positive and false negative findings were similar (10.7% and 9.0%, respectively). Surprisingly, the other statistical measures were not significantly different, i.e. true positive fraction was 67.1%, while ROC curve area index was Az = 0.76. The details are shown in Tables 2 and 3.
Average gM magnitude of microcalcification was 4.58 × 10‑5, while the average of all eligible maxima lines was 4.18 × 10‑5, leaving additional room for selection improvement based on the magnitude of general maxima. Similar conclusion holds for separately analyzed both malignant and benign clusters where average magnitudes corresponding to microcalcifications were 4.34 × 10−5 and 5.02 × 10−5 respectively while threshold averages were 4.12 × 10−5 and 4.23 × 10−5 respectively. The difference of average magnitudes 4.34 × 10−5 and 5.02 × 10−5 for malignant and benign microcalcifications may lead to microcalcification malignancy probability estimation in further research.
4.4. Fractal Analysis of Singularities in Breast Tissue
In the following sub-sections, we determine fractal dimension of selected singularities for 3 types of data-all detected singularities that resemble smoothed impulse function, detected smoothed impulse functions with dominant general modulus maxima, and the detected singularities that correspond to singularities in diagnosed microcalcification clusters.
Partition functions Z(q, a), q = 0 and 0.5 £ log2(a) £ 1.5, of all detected singularities in 25 microcalcification clusters are presented in Figure 8. The rhombi represent all singularities in all 25 analyzed microcalcification clusters. The squares represent all singularities with diagnosed malignant abnormalities in 12 clusters, while the triangles represent all singularities detected in remaining 13 clusters.
Specifically the slopes of log2(Z(0,a)) vs. log2(a), 0.5 £ log2(a) £ 1.5, correspond to the fractal dimension of the sets of singularities for all detected singularities (rhombi), as well as for 12 malignant (squares) and 13 benign (triangles) clusters. The trend-lines show the slope is close to 2 in all three analyzed datasets. Notice that in 2-D space, fractal dimension can not be considered higher than 2. The results show that the eligible singularities are uniformly distributed everywhere in the analyzed mammogram sub-images.
Similarly, the slopes of log2(Z(0,a)) vs log2(a), 0.5 £ log2(a) £ 1.5, corresponding to selected dominant singularities, as well as diagnosed microcalcification clusters are determined and shown in Table 4.
In the case of microcalcification clusters, dominant and diagnosed singularities have similar fractal dimension values (between 1.4 and 1.5), which indirectly supports the assumption that dominant eligible singularities point to microcalcifications. There is no difference between malignant and benign cluster fractal dimensions in 200 mm/pixel spatial resolution. Notice that for microcalcification cluster classification purpose spatial resolution 200 μm/pixel doesn’t allow zooming at 70 μm/pixel where microcalcification edge becomes visible and malignancy analysis by fractal dimension possible.
Dominant singularities in healthy areas have significantly lower fractal dimension, i.e. tending to 1 for the average of all 20 mammograms. Fractal dimension approaching 1 is the sign of linear structures typical for detected edges. Fractal analysis shows that smoother signal transition is uniformly distributed everywhere producing fractal dimension tending to 2 and 1.73 in normal and
Table 2. Abnormality detection statistics in 25 analyzed clusters.

Table 3. Microcalcification detection performance in 25 analyzed clusters.
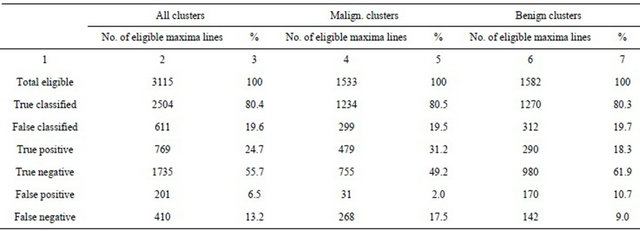
Table 4. Fractal dimmension of singularities in microcalcification clusters and healthy tissue.
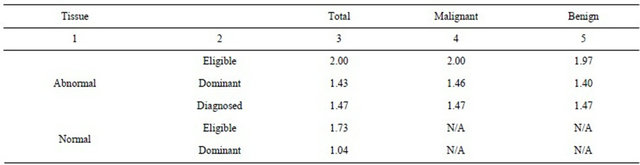
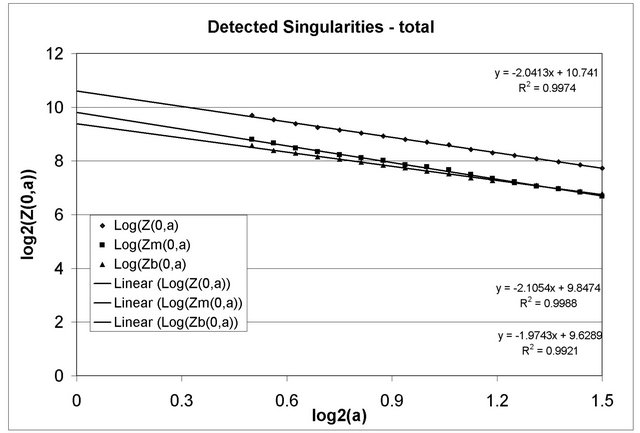
Figure 8. The fractal dimension for all detected singularities in the 25 analyzed microcalcification clusters in all, malignant, and benign sets of data (the slope of the partition function, q = 0 and a®0) is around 2, showing that the singular points are distributed everywhere in the clusters.
abnormal breast tissue respectively. On another hand fractal dimension of detected dominant signal transition in normal tissue is tending to 1 implying that the dominant singularities belong to the curve structures.
Healthy tissue fractal analysis shows that the set of all detected singularities has fractal dimension of 1.73 while the set of locally dominant singularities has fractal dimension tending to 1. This difference approves the significance of general modulus maxima in the detection of microcalcification. Fractal dimension of 1 is typical for the linear structures in the tissue and can be used in mammogram segmentation which we are proposing to be a future extension of this work.
Healthy tissue statistical analysis confirms our expectation that general maxima of normal fluctuation with negative Hölder exponent are lower than the general maxima belonging to the maxima lines representing the abnormalities suggesting that a combination of global and local thresholding need to be employed.
4.5. A Microcalcification Detection Simulation Example
Our proposed algorithm successfully localizes both malignant and benign microcalcification clusters and it is worth to notice that no other features but dominant general modulus maximum with local average threshold is employed in the detection of microcalcification clusters such as those shown in Figure 9.
Wang and Karayiannis [14] suggested detection of high frequency energy blobs with no differentiation between sharp transition characterized as smoothed impulse function and normal high frequency signal fluctuation in
 (a)
(a)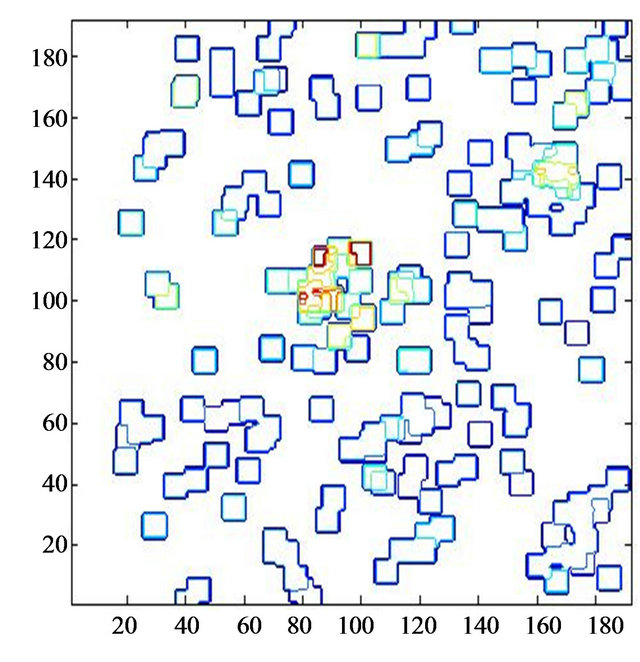 (b)
(b)
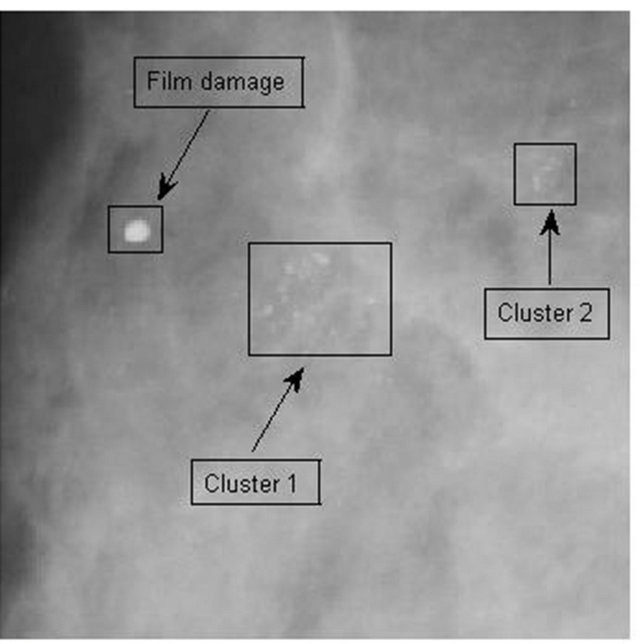
Figure 9. Mammogram mdb223 [24] with two microcalcification clusters and a film damage (a), and detected significant energy peaks are represented by yellow-orange-red iso-energy lines (b).
mammograms. Based on that idea we performed detection of energy blobs of detected dominant general modulus maxima. We consider that a microcalcification is a bright spot with a local intensity maximum in the neighborhood of a singular point related to the microcalcification and eliminate the singular point without a local intensity maximum in its neighborhood. The mammogram mdb223 [22] with two benign microcalcification clusters and a film damage is shown in Figure 9(a). The yelloworange-red iso-energy lines point to the suspicious spots with detected energy peaks as shown in Figure 9(b). Film damage was not disturbing the detection process, because of missing local maxima in the eligible neighborhood of the detected singularities in the border of film damage.
5. Conclusions and Future Work
Continuous wavelet transform was employed to detect singularities in mammograms by tracking modulus maxima along maxima lines across the scale and integrating it with fractal properties to differentiate between normal signal fluctuation and irregular ones in breast tissue.
Microcalcifications in mammograms were modeled by smoothed impulse function and detected by their negative Hölder exponent. Proposed procedure for maxima line classification enables selected general maxima to be analyzed by their magnitudes.
This method is capable to make difference between smooth signal transitions inevitable present in mammograms and microcalcification as sharper signal transition. Presented numerical results show that selecting maxima lines with negative Hölder exponent and local thresholding of general modulus maxima make possible the detection of the suspicious spots as local energy peaks of general modulus maxima.
Dominant general modulus maxima highly map into diagnosed microcalcifications in terms of local average magnitude and spatial distribution. Simulation results demonstrated that smoothed impulse function, recognized by their fractal properties of localized wavelet transform modulus maxima, can be considered a reliable feature for microcalcification detection in mammograms. Moreover, comparison of healthy and calcified breast tissue based on both statistical and fractal results show that selected general modulus maximum is a significant feature in microcalcification detection and classification.
Our results show that proposed metric for microcalcification detection is not sensitive on background tissue and therefore particularly convenient for dense parenchyma background in which microcalcification detection can be often a very challenging task.
Although a part of information has been lost by spatial resolution resampling from 50 mm to 200 mm microcalcifications preserve their smoothed impulse function nature, which has been detectable by proposed method. We showed that energy peaks in modulus maxima field correspond to microcalcification suspicious spots.
Coarse resolution makes faster suspicious spots searching procedure in real time during the screening procedure, which can be beneficiary by preventing an additional screening and saving the patients from having to endure the uncomfortable feelings during the procedure and more importantly, emotionally surviving cancer while waiting for additional test results.
Involving local intensity maximum of underlying mammogram in the neighborhood of detected smoothed impulse function significantly reduces false positive findings. Then the algorithm allows smaller threshold value of the general modulus maxima and therefore becomes more sensitive by detecting eligible smoothed impulse function with lower magnitude necessary for early detection of breast cancer.
The number of detected microcalcifications per area unit could be another feature that could reduce false positive findings.
Our findings in the difference of average general maxima magnitudes for malignant and benign microcalcifications leave a space for microcalcification malignancy probability estimation in further research. Namely, the numerical results show that general modulus maxima average of cancerous microcalcifications is lower than the average of benign ones. Lower modulus maximum magnitudes of cancerous findings make the detection more difficult, but open a space for improved classification in terms malignant vs. benign microcalcifications. Additional analysis might show that general maximum magnitude could serve as a parameter for malignancy probability estimation in real time.
The areas with microcalcification clusters tend to have higher fractal dimension than the healthy areas. Practical implementation of how to use fractal dimension in microcalcification detection and/or classification can be another interesting future work.
We showed that initial microcalcification segmentation could be performed based on wavelet transform modulus magnitude and phase and underlying mammogram in coarse resolution not significantly disturbed by noise. If necessary the microcalcification segmentation could be then refined in the finer resolution in which image acquisition was performed.
We found that our implementation of this proposed work including all parameter values is appropriate for the 200 μm/pixel spatial resolution and 8 bits/pixel numerical resolution. This approach could be easily applicable to other mammogram databases with different spatial and numerical resolution if proper adjustment to the estimates of the parameters values were taken into consideration.
Finally, involving additional microcalcification features could decrease false positive findings by enabling lowering modulus maximum threshold, which improves detection sensitivity of applied algorithm and therefore the general modulus maximum of smoothed impulse function can be used not only independently but also integrated with other microcalcification detection algorithms.
REFERENCES
- S. Mallat and W. L. Hwang, “Singularity Detection and Processing with Wavelets,” IEEE Transactions on Information Theory, Vol. 38, No. 2, 1992, pp. 617-643. doi:10.1109/18.119727
- S. Mallat and S. Zhong, “Characterization of Signals from Multiscale Edges,” IEEE Transactions on Pattern Analysis and Machine Intelligence, Vol. 14, No. 7, 1992, pp. 710-732. doi:10.1109/34.142909
- S. Mallat, “A Wavelet Tour of Signal Processing,” Academic Press, Waltham, 1999.
- Y. Meyer, “Un Contre-Exemple a la Conjecture de Marr et Celle de S. Mallat,” Preprint, 1991.
- E. B. Arneodo and J. F. Muzy, “The Thermodynamics of Fractals Revisited with Wavelets,” Physica A, Vol. 213, 1995, pp. 232-275.
- A. Arneodo, B. Audit, E. Bacry, S. Manneville, J. F. Muzy and S. G. Roux, “Thermodynamics of Fractal Signals Based on Wavelet Analysis: Application to Fully Developed Turbulence Data and DNA Sequences,” Physica A, Vol. 254, 1998, pp. 24-45. doi:10.1016/S0378-4371(98)00002-8
- N. Decoster, “Analyse Multifractale d’Images de Surfaces Rigueuses à l’aide da la Transformation en Ondolettes,” Ph.D. Thesis, L’Université de Bordeaux I, 1999. http://decoster.free.fr/phd
- A. Arneodo, N. Decoster and S. G. Roux, “A WaveletBased Method for Multifractal Image Analysis. I. Methodology and Test Applications on Isotropic and Anisotropic Random Rough Surfaces,” The European Physical Journal B, Vol. 15, 2000, pp. 567-600.
- S. Roux, J. F. Muzzy and A Arneodo, “Detecting Vorticity Filaments Using Wavelet Analysis: About the Statistical Contribution of Vorticity Filaments to Intermittency in Swirling Turbulent Flows,” The European Physical Journal B, Condensed Matter Physics, Vol. 8, No. 22, 1999, pp. 301-322.
- J. J. Heine and P. Malhotra, “Mammographic Tissue, Breast Cancer Risk, Serial Image Analysis, and Digital Mammography. Part 1. Tissue and Related Risk Factors,” Academic Radiology, Vol. 9, No. 3, 2002, pp. 298-316. doi:10.1016/S1076-6332(03)80373-2
- J. J. Heine and P. Malhotra, “Mammographic Tissue, Breast Cancer Risk, Serial Image Analysis, and Digital Mammography. Part 2. Serial Breast Tissue Change and Related Temporal Influences,” Academic Radiology, Vol. 9, No. 3, 2002, pp. 317-335. doi:10.1016/S1076-6332(03)80374-4
- M. Kallergi, “Computer-Aided Diagnosis of Mammographic Microcalcification Clusters,” Medical Physics, Vol. 31, No. 2, 2004, pp. 314-326.
- J. J. Heine, S. R. Deans, D. K. Cullers, R. Stauduhar and L. P. Clarke, “Multiresolution Statistical Analysis of HighResolution Digital Mammograms,” IEEE Transaction on Medical Imaging, Vol. 16, No. 5, 1997, pp. 503-515. doi:10.1109/42.640740
- T. C. Wang and N. B. Karayiannis, “Detection of Microcalcifications in Digital Mammograms Using Wavelets,” IEEE Transactions on Medical Imaging, Vol. 17, No. 4, 1998, pp. 498-509. doi:10.1109/42.730395
- W. Zhang, H. Yoshida, R. M. Nishikawa and K. Doi, “Optimally Weighted Wavelet Transform Based on Supervised Training for Detection of Microcalcifications in Digital Mammograms,” Medical Physics, Vol. 25, No. 6, 1998, pp. 949-956. doi:10.1118/1.598273
- R. N. Strickland and H. I. Hahn, “Wavelet Transforms for Detecting Microcalcifications in Mammograms,” IEEE Transactions on Medical Imaging, Vol. 15, No. 2, 1996, pp. 218-229. doi:10.1109/42.491423
- F. J. Gilbert, S. M. Astley, M. A. McGee, M. G. Gillan, C. R. Boggis, P. M. Griffiths and S. W. Duffy, “Single Reading with Computer-Aided Detection and Double Reading of Screening Mammograms in the United Kingdom National Breast Screening Program,” Radiology, Vol. 241, No. 1, 2006, pp. 47-53. doi:10.1148/radiol.2411051092
- P. Taylor, J. Champness, R. Given-Wilson, K. Johnston, and H. Potts, “Impact of Computer-Aided Detection Prompts on the Sensitivity and Specificity of Screening Mammography,” Health Technology Assessment, Vol. 9, No. 3, 2005, pp. 1-58.
- J. J. Fenton, S. H. Taplin, P. A. Carney, L. Abraham, E. A. Sickles, C. D’Orsi, E. A. Berns, G. Cutter, R. E. Hendrick, W. E. Barlow and J. G. Elmore, “Influence of ComputerAided Detection on Performance of Screening Mammography,” The New England Journal of Medicine, Vol. 356, 2007, pp. 1399-409. doi:10.1056/NEJMoa066099
- L. E. Philpotts, “Can Computer-Aided Detection Be Detrimental to Mammographic Interpretation?” Radiology, Vol. 253, No. 1, 2009, pp. 17-22.
- J. Tang, R. M. Rangayyan, J. Xu, I. E. Naqa and Y. Yang, “Computer-Aided Detection and Diagnosis of Breast Cancer with Mammography: Recent Advances,” IEEE Transactions on Information Technology in Biomedicine, Vol. 13, No. 2, 2009, pp. 236-251. doi:10.1109/TITB.2008.2009441
- J. Suckling, “The Mammographic Image Analysis Society Digital Mammogram Database,” Exerpta Medica International Congress, Vol. 1069, 1994, pp. 375-378. http://peipa.essex.ac.uk/info/mias.html
- B. Mandelbrot, “How Long Is the Coast of Britain? Statistical Self-Similarity and Fractional Dimension,” Science, New Series, Vol. 156, No. 3775, 1967, pp. 636-638.
- T. Netsch and H. O. Peitgen, “Scale-Space Signatures for the Detection of Clustered Microcalcifications in Digital Mammograms,” IEEE Transactions on Medical Imaging, Vol. 18, No. 9, 1999, pp. 774-786. doi:10.1109/42.802755

