Open Journal of Civil Engineering
Vol.04 No.04(2014), Article ID:52195,9 pages
10.4236/ojce.2014.44028
Effects of Pit-Sand on Resistance Capacities of Reinforced Concrete Space Framed Structures
Lekan Makanju Olanitori, Joseph Olaseinde Afolayan
Department of Civil Engineering, Federal University of Technology, Akure, Nigeria
Email: lekanolanitori@gmail.com
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 22 October 2014; revised 18 November 2014; accepted 29 November 2014
ABSTRACT
This paper used the existing formulae in estimating resistance parameter of reinforced concrete structure to assess the effect of concrete produced from pit-sand in Akure metropolis, on the resistance parameters of a collapsed building in Oba-Ile, Akure. Site inspections were carried out on the collapsed building, and concrete samples were taken. Both destructive and non-destructive methods were used to determine the structure’s concrete strength. The number of reinforcements in each structural element was determined by exposing them. Resistance parameters such as moments of resistance for slab (MRS), for beam (MRB) and shear capacity (VC) of the structural elements were estimated using existing formulae and, compare the results with the structure’s actual resistance parameters. The average concrete strength was 8.5 N/mm2 which was less than 20 N/mm2, the prescribed concrete strength for construction of the building. The estimated re- sistance parameters MRS, MRB and VC based on 8.5 N/mm2 concrete strength are 18.2 kN∙m, 46.3 kN∙m and 64.4 kN respectively. Also the estimated resistance parameters MRS, MRB and VC based on 20 N/mm2 concrete strength are 20.6 kN∙m, 54.1 kN∙m and 90.73 kN respectively. The actual MRS, MRB and VC at collapse were 6.67 kN∙m, 13.6 kN∙m and 18.88 kN respectively. The existing formulae for predicting resistance parameters did not give accurate resistance parameters for the building at collapse. The collapse of the building was by shear failure, since shear failure capacity will be reached first before any of the other resistance parameters.
Keywords:
Structure, Collapse, Load Capacity, Shear Capacity, Concrete

1. Introduction
In the past few years a considerable improvement have taken place in the understanding of structural concrete and has been incorporated in the revised codes of practice. The British Standard CP110: Code of Practice for the Structural Use of Concrete [1] , has superseded the British Standard Codes of Practice CP114 [2] , for reinforced concrete. Similarly, in America the ACI Standard ACI 318-71 [3] has replaced the previous standard ACI 318- 63 [4] . The major aspects of the revised codes is the limit state approach for designing reinforced concrete struc- tures and the separation of methods of concrete mix design procedures from that of concrete design considera- tions. However, in Nigeria, consultant structural engineers still make concrete specifications based on CP 114 [2] , which states concrete mixes of 1:2:4, 1:1½:3 and 1:1:2 produces concrete with compressive strength of 21 N/mm2, 25.5 N/mm2 and 30 N/mm2 respectively at 28 days. However, Olanitori and Olotuah [5] show that these compressive strengths might not be attained due to the clay/silt content of sand, which negatively affects the compressive strength of concrete produced from them.
In CP110 [1] and BS8110 [6] , this portion of CP114 [2] that dealt with concrete mix prescription was ex- punge from the code and standard. This is to the superior knowledge that concrete produced from different types of sand but of same mix proportion will produce concrete with different strengths. With the publication of BS8110 in 1985 [6] , CP110 [1] was withdrawn. The publication of CP110 [1] and BS8110 [6] were accompa- nied with several BS standards which dealt with different aspects of concrete production [7] .
The quality of concrete produced depends on the quality of its constituent materials and their mix ratios, the higher the percentage of clay/silt contents of sand, the lower the characteristic strength [5] . To mitigate the effect of clay/silt content of sand on the strength of concrete produced from it, there is need to increase the cement content of the concrete, depending on the clay/silt percentage [8] . Olanitori, 2012 [9] determines the cost impli- cation of mitigating the effect of clay/silt content of sand using mathematical models. In order to improve the quality of concrete produced from locally available aggregates, there is the need to have indigenous codes of practice, which will take into consideration the quality of the available aggregates [7] .
The collapse of most reinforced concrete structures is by shear failure at the beam-column joint and sudden in nature [10] . In 1962, Joint ACI-ASCE Committee 326 [11] published a report regarding the design and behavior of beams failing due to shear and diagonal tension. To develop safe design recommendations, a database of 194 beam tests without shear reinforcement was compiled. The database consisted of 130 laboratory specimens tested under single-and double point loads and 64 beams subjected to uniformly distributed loads. Based on those data, design equation was formulated and is included in ACI 318-05 [12] and presented as Equation (1).
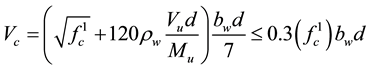 (1)
(1)
where
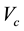 is the nominal shear strength provided by concrete;
is the nominal shear strength provided by concrete;
 is the specified compressive strength of
is the specified compressive strength of
concrete;
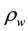 is the ratio
is the ratio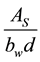 ; Vu is the factored shear force at section; Mu is the factored moment at section;
; Vu is the factored shear force at section; Mu is the factored moment at section;
bw is the web width; d is the effective depth of section; and As is the area of tension reinforcement.
By neglecting the term
 in Equation (1) a simplified but conservative version could be derived and pre- sented as Equation (2).
in Equation (1) a simplified but conservative version could be derived and pre- sented as Equation (2).
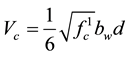 (2)
(2)
To include the effects of loading type and shear span to depth ratio into current code provisions, for members in which more than 1/3 of the factored shear at the critical section results from concentrated load located be- tween 2d and 6d of the face of the support, Brown et al. [13] , proposes:
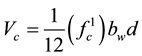 (3)
(3)
Such a reduction in shear strength as indicated in Equation (3) will substantially reduce the number of tests that fall below code values.
According to Arslan [14] , the nominal shear strength provided by concrete can be estimated using Equation (4).
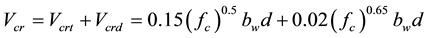 (4)
(4)
where:
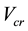 is the cracking shear strength,
is the cracking shear strength,
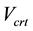 is the diagonal tension cracking strength and
is the diagonal tension cracking strength and
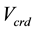 is the dowel strength.
is the dowel strength.
Based on the principal shear strength Vo carried in the compression zone, considering the influence of para- meters; the slenderness ratio (a/d) and size effect (1/d), Arslan, 2012 [15] expresses the diagonal cracking strength of RC slender beams without stirrups as given in Equation (5).
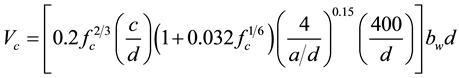 (5)
(5)
where c is the depth of the neutral axis.
Other existing shear strength models for slender beams without stirrups, by Kim and Park, 1996 [16] , Khuntia and Stojadinovic, 2001 [17] , and Rebeiz, 1999 [18] are presented in Table 1.
The ACI 318-08 [19] design shear strength is a simple superposition of transverse reinforcement and concrete strength. The design strength is independent of whether flexural yield has occurred prior to shear failure. For members, design shear strength is calculated using Equation (6).
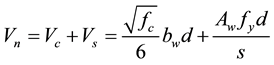 (6)
(6)
where Vc is the contribution of concrete to shear strength; Vs is the contribution of shear reinforcement to shear strength; fc is the compressive strength of concrete; Aw is the area of shear reinforcement within a distance s and fy is the shear reinforcement yield strength. The contribution of shear reinforcement is derived from basic equili- brium considerations on a 45-degree truss model with constant shear reinforcement spacing and an effective depth.
In their work,Arslan and Polat [20] , show that there exists a significant amount of contribution of concrete to the shear strength (18% - 69%), however, noted further experiments should be conducted with a wider range of shear reinforcement ratio, shear span-to-depth ratio, concrete strength and various loading schemes in order to obtain more reliable assessments.
Since the mid-1980s, there is an increasing amount of experimental evidence showing that the underlying concepts of the provisions of current codes (for example, BS 8110-1985 [6] and ACI 318-05 [12] ) for the shear in particular and, to a certain extent for the flexural design of reinforced concrete (RC) structures are in conflict with fundamental properties of concrete at both the material and the structural levels [21] . Also, only few of the existing shear strength models give reasonable shear strength capacity for reinforced concrete structures con- structed from concrete produced from locally available aggregates.
Table 1. Some of the existing shear strength models for slender beams without stirrups.
A lot of work has been carried out to determine the effect of the various types of pit-sand on the cube strength of concrete, however very little work from literature has been carried out to determine the effect of the various types of pit-sand on the resistance capacities of reinforced concrete space framed structures. This paper, using existing formulae from the codes, the estimated and actual resistance capacities of the collapsed building at Oba-Ile were determined, in order to determine the effect of the pit-sand used on the resistance capacities.
2. Materials and Methods
2.1. Materials
The materials used for this study are structural detailing, portable rotary drilling machine, 15 samples of 75 mm diameter cores of concrete, PUNDIT6 equipment, and a manually operated universal testing machine. The client of the collapsed building was not willing to provide the architectural plan and structural detailing. Consequen- tially, as-built architectural plan and the structural detailing were produced from site inspection and by exposing the structural components such as slab, beams and columns. Result of the site inspection given in Table 2 and Figure 1 shows some part of the collapsed building.
2.2. Procedure
Fifteen samples of 75 mm diameter cylindrical cores of concrete were taken from slabs, beams and columns. Five samples were taken from each structural element. The cores were vertically and horizontally drilled with a portable rotary drilling equipment using water as the drilling fluid and diamond impregnated bit. The retrieved cores were taken to the laboratory for examination and tested for strength using Universal Testing Machine (UTM) in accordance with BS 1881-120, 1983 [22] . Also non-destructive tests were carried out on parts of the building that are yet to collapse using PUNDIT 6 in accordance with BS 1881 [23] [24] . The compressive strengths from UTM and the PUNDIT6 are presented in Table 3, while the characteristic strengths from UTM and the PUNDIT6 are presented in Table 4.
2.3. Method of Analysis
From the as-built structural drawing, using equations in the code, moment of resistance of the slab and beam as
Figure 1. Collapsed part of the building.
Table 2. The summary of the areas of tension reinforcement provided for the structural elements of the collapsed building and the structural re-assessment.
Table 3. Results from universal testing machine and the PUNDIT 6.
Table 4. Characteristic strengths from universal testing machine and the PUNDIT6.
well as the shear capacity of the beam were estimated and presented in Table 5. The estimated moment of resis- tance and the shear capacity were compared with actual moment of resistance and the shear capacity. Also shear capacity of the collapse building was evaluated based on the existing shear strength models for slender beams without stirrups (and presented in Table 6), and compared with that of the estimated and actual shear capacities.
3. Moment of Resistance (Mr) and Shear Capacity (Vc)
3.1. Estimated Moment of Resistance for Slab and Beam (MER)
The moment of resistance of the slab and beam is estimated using Equation (7) below:



Equations (14) and (15) of BS 8110-1, 1997 [25] can be written in a compressed form, thus having;

m is the maximum design ultimate moments either over supports or at mid-span on strips of unit width and span (lx or ly).
βs is the sagging (or hogging) moment in the spans (or over the edges), per unit width, in the direction of shorter spans/edges (or longer spans/edges), divided by
n is the slab load and, lx is the shorter span.
Using Equation (8)


For a continuous beam, the maximum moment occurs at the middle of end span, hence

where F is the total design ultimate load and, L is the effective span.
Table 5. Resistance parameters of the collapsed building.
MRS―moment of resistance of slab; MRB―moment of resistance of slab; NPCL―partial collapse load; NTC―total collapse load; VC―shear capacity.
Table 6. Shear capacities determined from existing shear strength models.
VCACS―shear capacity, determined using actual concrete strength; VCPCS―shear capacity, determined using prescribed concrete strength.
Using Equation (9), we have:

Equating MERB and MRB, w can be determined. Where w is the beam load in kN/m.


Using equation 10, the equivalent slab load on beam can be estimated.

where n is the slab load and, lx is the shorter span of the slab supported by the beam.
where nesl is the estimated equivalent slab collapse load on beam (Total Collapse Load).
These results are presented in Table 5.
3.2. Estimated Shear Capacity of Beam (VEB)
The shear capacity of a section for a given stirrup size and spacing can be estimated by Equation (11):

Using Equation (11) above, we have:
This result is presented in Table 5.
3.3. Moments of Resistance, Load and Shear Capacities, of the Collapsed Space Framed Building
3.3.1. Collapse Load of the Space Framed Building
At collapse, the load acting on the structure is estimated as follows:
Slab load = 0.15 × 24 = 3.6 kN/m2. Live load during construction = 1.5 kN/m2. Collapse slab load ns = 1.4 × 3.6 + 1.6 × 1.5 = 7.44 kN/m2.
Load due to beam weight =

Using above loadings, Equations (8) and (9) can be used to determine the maximum span moments for slab and beam respectively.
The maximum shear force acting on a beam can be estimated using Equation (12).

where w is the uniformly distributed load on beam and, l is the beam span. Hence using Equation (12):
These results are presented in Table 5.
3.3.2. Moment of Resistance Using Analysis of Section Method
Average characteristic strength
4. Analysis and Discussion of Results
From Table 2, the results of the structural re-assessment show that tension reinforcements provided for the slab were adequate. Also, the longitudinal reinforcements provided for the beams were equally adequate, while that of shear reinforcement was not adequate. The reinforcements provided for the columns were adequate.
Table 3 shows the results of universal testing machine and the PUNDIT6, while Table 4 gives the characte- ristic strength of the concrete from which the collapsed building was built as 8.8 N/mm2 and 8.2 N/mm2 for PUNDIT6 and Universal Machine respectively, resulting in an average characteristic strength of 8.5 N/mm2. The prescribed design concrete strength for the building was 20 N/mm2. This shows a 57.5% reduction in the concrete strength caused by the low quality of pit-sand used for the construction.
The estimated resistance parameters, such as moment of resistance (MR), shear capacity (VC) and collapse load (NC) of the building were estimated using equilibrium equation of a reinforced concrete section with the pre- scribed and actual characteristic strengths of concrete which equal 20 N/mm2 and 8.5 N/mm2 respectively. The analysis equations of the BS 8110-1, 1997 [25] were used to determine the actual resistance parameters of the collapsed building using the actual collapse load. The estimated and actual resistance parameters of the col- lapsed building were presented in Table 5.
From Table 5, the moments of resistance of slab (MRS) estimated from equilibrium equation of a reinforced concrete section, using the prescribed strength of concrete (RPCS), actual collapse load (RACL) and, actual con- crete characteristic strength (RACCS) are 20.6 kN∙m, 6.67 kN∙m and 18.2 kN∙m respectively. Also, the moment of resistance of beam (MRB) determined using (RPCS), (RACL) and, (RACCS) are 54.1 kN∙m, 13.6 kN∙m and 46.3 kN∙m respectively.
Also, from Table 5, partial collapse load (NPCL) determined from the values of (RPCS), (RACL) and, (RACCS) are 23.0 kN/m2, 7.44 kN/m2 and 12.6 kN/m2 respectively. Also, the total collapse load (NTCL) from (RPCS), (RACL) and, (RACCS) values are 37.5 kN/m2, 7.44 kN/m2 and 32.2 kN/m2 respectively, while the shear capacity (VC) from (RPCS), (RACL) and, (RACCS) values are 90.73 kN, 18.88 kN and 64.4 kN respectively.
From the above, the estimated moments of resistance of slab (MRS) determined from RPCS, and RACCS are 20.6 kN×m and 18.2 kN×m respectively, and greater than that determined from RACL, which equals 6.67 kN×m by 209% and 173% respectively. Equally, the estimated moments of resistance for beam (MRB), determined from RPCS and RACCS are 54.1 kN×m and 46.3 kN×m respectively, and greater than that determined from RACL, which equals 13.6 kN×m by 298% and 240% respectively.
The partial collapse loads (NPCL) determined from RPCS and RACCS are 23.0 kN/m2 and 12.6 kN/m2 respectively, and greater than that determined from RACL, which equals 7.44 kN/m2 by 209% and 69% respectively. The total collapse loads (NTCL) determined from RPCS and RACCS are 37.5 kN/m2, and 32.2 kN/m2 respectively, and greater than RACL, which equals 7.44 kN/m2 by 404% and 333% respectively. Also, the shear capacity, determined from RPCS and RACCS are 90.73 kN and 64.4 kN respectively, and greater than that determined from RACL, which equals 18.88 kN, by 381% and 241% respectively.
The estimated moments of resistance of slab (MRS) determined from RPCS and RACCS are 20.6 kN×m and 18.2 kN×m respectively. This shows that, when the strength of concrete decreases by 57.5% (20 N/mm2 to 8.5 N/mm2), MRS only decreases by 12%. Also decrease by 57.5% in concrete strength, only have decrease effect of 14.4% on MRB. Decrease in concrete strength by 57.7% only has decease effect of 14.1% on the total collapse load (NTCL). The shear capacity determined from RPCS and RACCS are 90.73 kN and 64.4 kN respectively, hence the decrease effect of 57.7% of concrete strength is 29%.
Table 6 shows shear capacities determined from existing shear strength models. Only the shear strength mod- els of Brown et al. [13] and Kim and Park [16] give shear capacities of 22.6 kN and 20.4 kN respectively, which compares favorably with the actual shear capacity of the collapsed building which equals 18.88 kN. The shear capacities from Brown et al. [13] and Kim and Park [16] , defer from that of the actual shear capacity by 8.1% and 19.7% respectively.
Table 7 shows the percentage increment of resistance parameters over that due to the actual collapse load. From Table 7, shear capacity VC has the highest percentage of increment; hence shear failure capacity will be reached first before any others in resistance parameters of the collapsed building. Therefore, the collapse of the building is by shear failure which is sudden in nature.
5. Conclusions
From the discussion above, the following conclusions can be drawn:
1) The collapse of the building was caused by shear failure which is sudden in nature.
2) Method of analysis of section, for reinforced concrete structures, gives overestimated values of the resis- tance parameters.
3) Coefficient method gives more accurate values of the resistance parameter.
4) Shear strength models of Brown et al. (2006) and Kim and Park (1996) give the most accurate value of shear capacity of reinforced concrete at failure.
5) The estimated resistance capacities, determined using the actual concrete characteristic strengths, gives an overestimated resistance capacities when compared with the actual resistance capacities. This shows that there is the need to investigate the effect characteristic concrete strength on resistance capacities of reinforced concrete space framed structures.
Table 7. Percentage increment of resistance parameters over that due to collapse load.
6. Recommendations
1) Local Codes of Practice should be developed so as take into consideration, the quality of the locally availa- ble aggregates in formulating design formulae, which will be capable of given more realistic resistance parame- ters.
2) Effect of the reduction of the characteristic strength of concrete should be investigated, and appropriate measures should be put in place so as to produce safe reinforced concrete structures.
References
- CP 110 (1972) Code of Practice for Structural Use of Concrete: Part I―Design, Materials and Workmanship. British Standards Institution, London.
- CP 114 (1957) The Structural Use of Reinforced Concrete in Buildings (Amended in 1965). British Standards Institution, London.
- ACI Committee 318 (1971) Buildings Code Requirement for Reinforced Concrete. American Concrete Institute, Detroit.
- ACI Committee 318 (1963) Buildings Code Requirement for Reinforced Concrete. American Concrete Institute, Detroit.
- Olanitori, L.M. and Olotuah, A.O. (2005) The Effect of Clayey Impurities in Sand on the Crushing Strength of Concrete (a Case Study of Sand in Akure Metropolis, Ondo State, Nigeria). Proceedings of 30th Conference on “Our World in Concrete and Structures”, Singapore City, 23-24 August 2005, 373-376.
- BS 8110 (1985) Structural Use of Concrete: Part―I: Code of Practice for Design and Construction. British Standards Institution, London.
- Olanitori, L.M. (2013) Codes of Practice: Prerequisite for Quality Structural Design and Management of Buildings in Nigeria. 5th West Africa Built Environment Research (WABER) Conference, Accra, 12-14 August 2013, 283-291.
- Olanitori, L.M. (2006) Mitigating the Effect of Clay Content of Sand on Concrete Strength. Proceedings of 31st Con- ference on Our World in Concrete and Structures, Kaula Lumpur, 15-17 August 2006, 344-352.
- Olanitori, L.M. (2012) Cost Implication of Mitigating the Effect of Clay/Silt Content of Sand on Concrete Compressive Strength. Journal of Civil Engineering and Urbanism, 2, 143-148.
- Olanitori, L.M. (2011) Causes of Structural Failures of a Building: Case Study of a Building at Oba―Ile Akure. Journal of Building Appraisal, 6, 277-284.
- Joint ACI-ASCE Committee 326 (1962) Shear and Diagonal Tension. A CI Journal Proceedings, 59, 1-30.
- ACI Committee 318 (2005) Building Code Requirements for Structural Concrete and Commentary (ACI 318R-05). American Concrete Institute, Farmington Hills.
- Brown, M.D., Bayrak, O. and Jirsa, J.O. (2006) Design for Shear Based on Loading Conditions. ACI Structural Journal, 103, 541-550.
- Arslan, G. (2008) Cracking Shear Strength of RC Slender Beams without Stirrups. Journal of Civil Engineering and Management, 14, 177-182. http://dx.doi.org/10.3846/1392-3730.2008.14.14
- Arslan, G. (2012) Diagonal Tension Failure of RC Beams without Stirrups. Journal of Civil Engineering and Management, 18, 217-226. http://dx.doi.org/10.3846/13923730.2012.671264
- Kim, J.K. and Park, Y.D. (1996) Prediction of Shear Strength of Reinforced Concrete Beams without Web Reinforcement. ACI Materials Journal, 93, 213-222.
- Rebeiz, K.S. (1999) Shear Strength Prediction for Concrete Member. Journal of Structural Engineering ASCE, 125, 301-308. http://dx.doi.org/10.1061/(ASCE)0733-9445(1999)125:3(301)
- Khuntia, M. and Stojadinovic, B. (2001) Shear Strength of Reinforced Concrete Beams without Transverse Reinforcement. ACI Structural Journal, 98, 648-656.
- ACI Committee 318 (2008) Building Code Requirements for Structural Concrete and Commentary (ACI 318R-08). American Concrete Institute, Farmington Hills.
- Arslan, G. and Polat, Z. (2013) Contribution of Concrete to Shear Strength of RC Beams Failing in Shear. Journal of Civil Engineering and Management, 19, 400-408. http://dx.doi.org/10.3846/13923730.2012.757560
- Kotsovs, M.D. (2007) Concepts Underlying Reinforced Concrete Design: Time for Reappraisal. ACI Structural Journal, 104, 675-684.
- BS 1881 (1983) Testing Concrete―Part 120: Method for Determination of the Compressive Strength of Concrete Cores. British Standards Institution, London.
- BS 1881 (1986) Testing Concrete―Part 201: Guide to the Use of Non-Destructive Methods of Test for Hardened Con- crete. British Standards Institution, London.
- BS 1881 (1986) Testing Concrete―Part 203: Recommendations for the Measurement of Velocity of Ultrasonic Pulses in Concrete. British Standards Institution, London.
- BS 8110 (1997) Structural Use of Concrete―Part 1: Code of Practice for Design and Construction. British Standards Institution, London.












