Open Journal of Civil Engineering
Vol.4 No.3(2014), Article
ID:49314,12
pages
DOI:10.4236/ojce.2014.43019
Assessment of Cyclic Resistance Ratio (CRR) in Silty Sands Using Artificial Neural Networks
Hassan Sharafi1*, Sahar Jalili2
1School of Faculty Engineering, Razi University, Kermanshah, Iran
2Department of Civil Engineering, College of Agriculture, Kermanshah Branch, Islamic Azad University, Kermanshah, Iran
Email: *h_sharafi@razi.ac.ir
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 25 June 2014; revised 30 July 2014; accepted 13 August 2014
ABSTRACT
In this study, a backpropagation neural network algorithm was developed in order to predict the liquefaction cyclic resistance ratio (CRR) of sand-silt mixtures. A database, consisting sufficient published data of laboratory cyclic triaxial, torsional shear and simple shear tests results, was collected and utilized in the ANN model. Several ANN models were developed with different sets of input parameters in order to determine the model with best performance and preciseness. It has been illustrated that the proposed ANN model can predict the measured CRR of the different data set which was not incorporated in the developing phase of the model with the good degree of accuracy. The subsequent sensitivity analysis was performed to compare the effect of each parameter in the model with the laboratory test results. At the end, the participation or relative importance of each parameter in the ANN model was obtained.
Keywords:Liquefaction, Cyclic Tests, Neural Networks, CRR, Silty Sands

1. Introduction
Cyclic Resistance Ratio (CRR) is one of the fundamental parameters in the prediction of liquefaction phenomenon, frequently observed during many moderate to strong earthquakes in sand-silt mixture deposits. This parameter can be determined using cyclic tests on the undisturbed or reconstituted laboratory specimens.
In recent years, the application of artificial neural networks (ANNs) for the solution of variety of geotechnical engineering problems has been the focus of many researchers. The method of artificial neural networks essentially involves the mapping of a complex input pattern with another complex output pattern using data processing models made up of extensively interconnected neurons [1] . Artificial Neural Networks (ANN), a powerful tool for statistical data manipulation, have been used in many complicated geotechnical engineering problems such as stress-strain modeling of soils, piles bearing capacity, settlement of shallow foundations, earthquake induced liquefaction and seismic lateral spreading [1] [2] . Considering of the high complexity and multiparameter dependence of soil response, relatively simple, but robust, feed-forward neural network models trained by back propagation algorithms have found wide usage in the field of geotechnical engineering [3] -[5] . Recently, many researchers [6] -[9] have implemented the ANN model in the assessment of liquefaction resistance of sands. For example, a simplified method proposed by Juang et al. [10] , based on cone penetration test (CPT) data, clearly illustrated the potential applicability and suitability of ANNs in the assessment of liquefaction resistance. Rahman and Wung [11] have also contributed to this area of research by developing a neural network model based on standard penetration test (SPT) data. As indicated earlier, data from laboratory element tests provides another avenue for understanding the cyclic loading response of soils in a fundamental manner [12] [13] . Young-Su, and Byung-Tak [14] have attempted to use a limited number of element test results in the ANN model to explain the parameters affecting CRR. However, no comprehensive study has yet been conducted to examine a wide-range laboratory test results on liquefaction resistance ratio (CRR) using ANN as a framework.
Based on these considerations, this study introduces a new ANN model, developed to predict liquefaction resistance of sand mixture with silt using published cyclic triaxial, hollow torsional and direct simple shear (DSS) tests data for various different sands. In essence, the model presents a characteristic relationship between the cyclic resistance ratio (CRR) and the parameters affecting liquefaction triggering.
After investigating a number of models based on different combinations of input soil parameters, the final ANN model with best predication capability was proposed and parametric study was performed to verify the credibility of the model.
2. Database Used for the Development of ANN Model
In order to present a general and well-built ANN-based model for various types of soils with various initial states, a wide-range database was collected from previously published cyclic tests. Baziar and Sharafi [15] -[17] collected database contains parameters on the cyclic stress ratio and Liquefaction resistance. They carried out extensive tests for the complete database. In their experiments, the effect of the fines content on liquefaction strength and energy for liquefaction were investigated. They showed also effect fines content on the cyclic stress ratio (CSR) and cyclic resistance ratio (CRR). The database contains 540 cyclic triaxial, 121 cyclic torsional shears and 6 cyclic simple shear tests [18] -[25] . The criteria for failure (liquefaction triggering) is initial liquefaction ( ) or double amplitude of strain of 5% (
) or double amplitude of strain of 5% ( ), whichever occurs first. The main information from the tests needed for this study include; initial effective mean confining pressure,
), whichever occurs first. The main information from the tests needed for this study include; initial effective mean confining pressure, 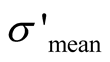 (kPa), initial relative density after consolidation,
(kPa), initial relative density after consolidation, 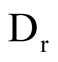 (%), percentage of fines content, FC(%), void ratio, e, the number of cycle of liquefaction, Nl, and measured cyclic resistance ratio required for liquefaction triggering, CRR. The range of parameters used for this study is presented in Table1 From this table, it can be seen that
(%), percentage of fines content, FC(%), void ratio, e, the number of cycle of liquefaction, Nl, and measured cyclic resistance ratio required for liquefaction triggering, CRR. The range of parameters used for this study is presented in Table1 From this table, it can be seen that  varies between 50 and 400 kPa, while
varies between 50 and 400 kPa, while 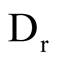 and FC are varying between −44.5% to 105.1% and 0% to 100%, respectively. Also, e and Nl range from 0.25 to 1.77 and from 0.6 to 10,000 respectively. In addition, the data set collected in this study contains data of some element tests under random loading (non-harmonic).
and FC are varying between −44.5% to 105.1% and 0% to 100%, respectively. Also, e and Nl range from 0.25 to 1.77 and from 0.6 to 10,000 respectively. In addition, the data set collected in this study contains data of some element tests under random loading (non-harmonic).
3. Neural Network Development
The database was randomly divided into two separate groups denoted as training and testing sets consisting about 70% and 30% of data, respectively. The testing set was utilized to determine when training should be stopped to avoid over fitting. In order to obtain a consistent data division, several combinations of the training and testing sets were experienced. The above selection was such that the maximum, minimum, mean and standard deviations of parameters were consistent in training and testing data sets (Table 1).
Table 1. Statistical characteristics of consistent training and testing sets.
aMaximum; bMinimum; cStandard Deviation.
The network was trained with the back propagation algorithm. In seeking the most appropriate model, the minimum mean square error goal was set at a constant value of 0.01 and the number of hidden neurons for each ANN model was varied. The model with maximum R2 and minimum root mean square error (RMSE) was considered as the optimal ANN model. In the present study, one hidden layer was adopted and the number of hidden neurons considered for each ANN model ranged between 10 and 15. To overcome the network “memorizing or over-fitting,” there are a number of approaches including random re-sampling, and cross validation. The crossvalidation approach was used here to determine the best network structure in this study.
The model architecture was built with one hidden layer, a learning rate of 0.05 updated with a coefficient of 1.05 after each epoch, and a momentum term of 0.9 updated with a coefficient of 0.9 after each epoch. The input vector was fully connected to the hidden neurons by a tan-sigmoid transfer function and the neurons of hidden layer were fully connected to the output layer via a linear function. Input vector contained soil initial parameters and output (the target vector), cyclic resistance ratio required to trigger liquefaction (CRR). In order to obtain a more efficient training process, the input and target were standardized to have zero mean and unity standard deviation. Cross-validation or employing another set of data for more testing can be used to increase the generality of the models for future predictions. In the prediction of CRR for this study, maximum of five inputs with different combination were considered. In fact, several ANN models using element tests data were constituted for predicting the CRR and among them, the model with better performance (R2-correlation factor greater coefficient of determination and smaller MSE and MAE) for validation data set was selected. In other words, the ANN models were developed with the best performance concurrently for training, testing and validation data sets. Since, the models were only generated based on the element tests data and validated by the centrifuge tests, it is reasonable to anticipate that the model would be generalized enough to predict real earthquake induced liquefaction triggering. An extensive trial study was performed to select the most relevant input parameters for the ANN model. Five different ANN models were developed using different combinations of input parameters as indicated in Table2 It can be seen from this Table that, except for Model 2, performances of the models are generally getting worse when input parameters are decreased.
4. Results and Discussion
According to Table 2, it can be seen that Models 1 and 2, are the most appropriate model to estimate the cyclic resistance ratio (CRR). As it is evident from this Table, correlation coefficient (R2) in these two models are more than other models regarding four categories of; training data, testing data, all data and validation data. Therefore, any of these two models can be selected as a model for predicting the cyclic resistance ratio (CRR). Model 1 is with five and Model 2 is with four parameters respectively. Table 3 summarizes the two more appropriate ANN models with their selected input parameters. For these two models, the values of R2, MSE and MAE for all data set are shown in this Table.
Model 2, however, seems more suitable due to the following reasons:
1) The number of parameters in Model 2 is less than Model 1 2) Correlation coefficient (R2) in Model 2 is greater than Model 1 3) Two-parameters of; relative density (Dr) and void ratio (e), in Model 1 present almost the same soil characteristics.
Table 2. Artificial neural network models used in this study.
Table 3. Summary of appropriated two ANN models developed for various input parameters.
Based on this successful performance, Model 2 with 4 input neurons, 15 hidden neurons, and 1 output neuron were selected for the final predictions. Values of R2, MSE and MAE, produced from this model were 0.9, 0.58%, 5.24% respectively for all element tests data and 0.9%, 0.78%, 3.38% for validation tests data. Figures 1-3 illustrate the measured and predicted Cyclic Resistance Ratio values (CRR) for training, testing and all element test data, respectively for the proposed Model (Model 2).
For validation model was used two set data, element test data and centrifuge test data. Figure 4 shows results model for element tests data that these element test data are not used in the designed model. As it is seen, the prediction of the proposed Model, which has been designed based on only the element tests, is very good for the new element tests. Dief [26] performed several centrifuge tests on Nevada and Reid Bedford clean sands and LSFD silty sand. He processed the recorded accelerations and lateral displacements of the laminar box segments using lumped mass models and estimated the shear stress-strain history at different depths in centrifuge models. Due to unavailability of information for all his tests, only three tests with their needed information reported by him, were selected for the validation of the proposed model. Predicted Cyclic Resistance Ratio (CRR) by ANN model versus measured values for validation data set is showed at Figure 5. As it is seen, the prediction of the proposed Model, which has been designed based on only the element tests, is very good for the centrifuge tests. Density (Baziar and Sharafi, 2011).
5. Parametric Study
For further verification of the ANN model, a sensitivity analysis was performed in this study. The main goal was to find the effect of each parameter on the values of the cyclic resistance ratio (CRR) while generating liquefaction. This parametric study was carried out also to find variations of cyclic resistance ratio (CRR) in the range of soil parameters values cited in Table 1 with other parameters kept constant at their average values. Similar to laboratory studies carried out by pioneers [27] -[31] on the dependency of liquefaction resistance of sands on initial relative density and effective confining stress, the results of the parametric study for the proposed model
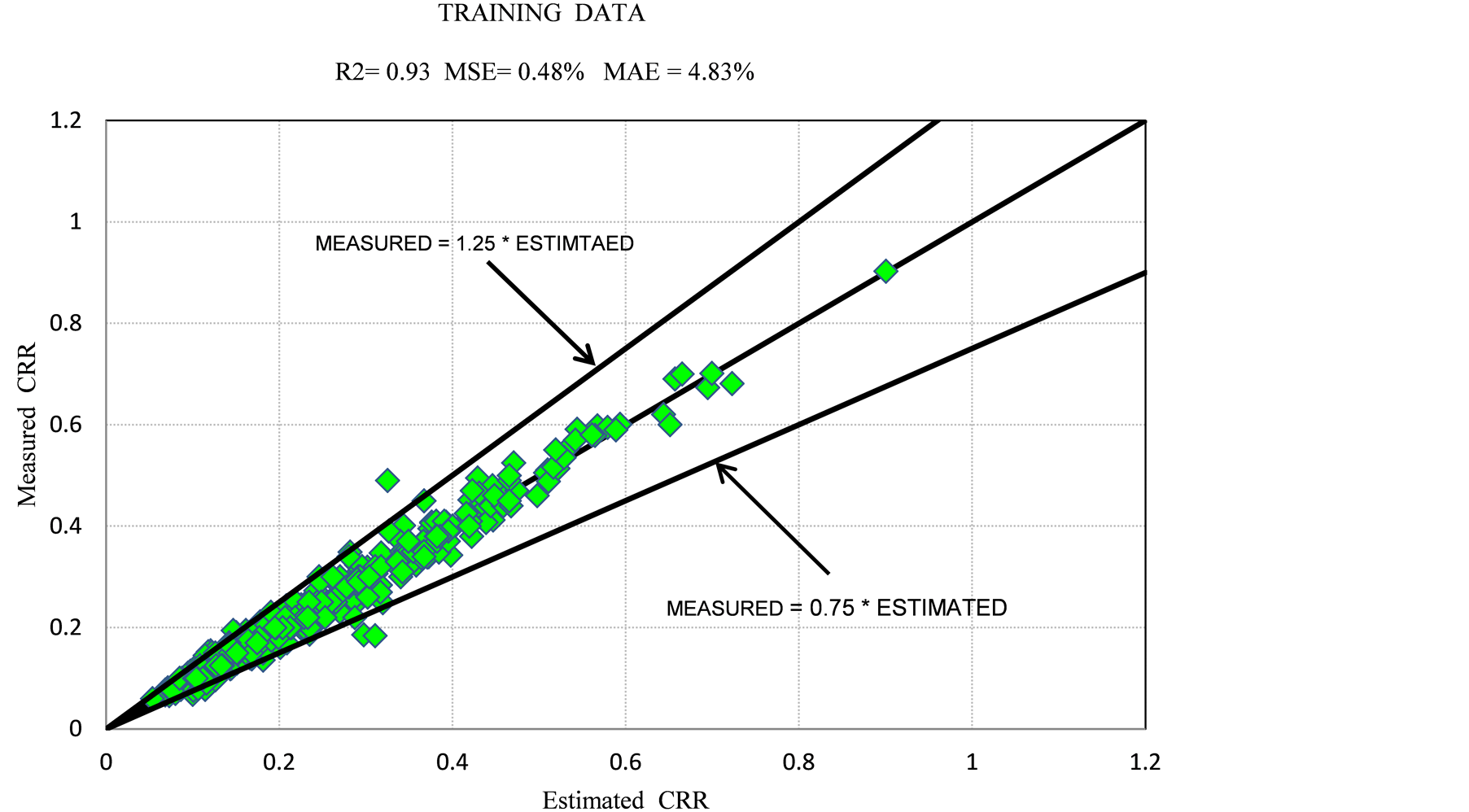
Figure 1. Predicted CRR by ANN model versus measured values for training data.

Figure 2. Predicted CRR by ANN model versus measured values for testing data.
confirmed that the cyclic stress ratio of sands continuously increased with increasing initial relative density or effective confining stress while other parameters were kept constant. The parametric studies for three variation confining pressure, relative density and fines content with constant other factors were performed. Figures 6-8 were showed result of parametric study for confining pressure, relative density and fines content. The effect of confining pressure on the cyclic resistance can be mentioned confining pressure increases, the liquefaction resistance of silty sands decreases (Figure 9) [25] and with increasing relative density, the cyclic resistance ratio (CRR) was increased (Figure 10) [12] [35] . The effect of non-plastic FC on the liquefaction behavior of sand-silt mixtures is more complex than the effect of other variables. Several researchers have claimed that
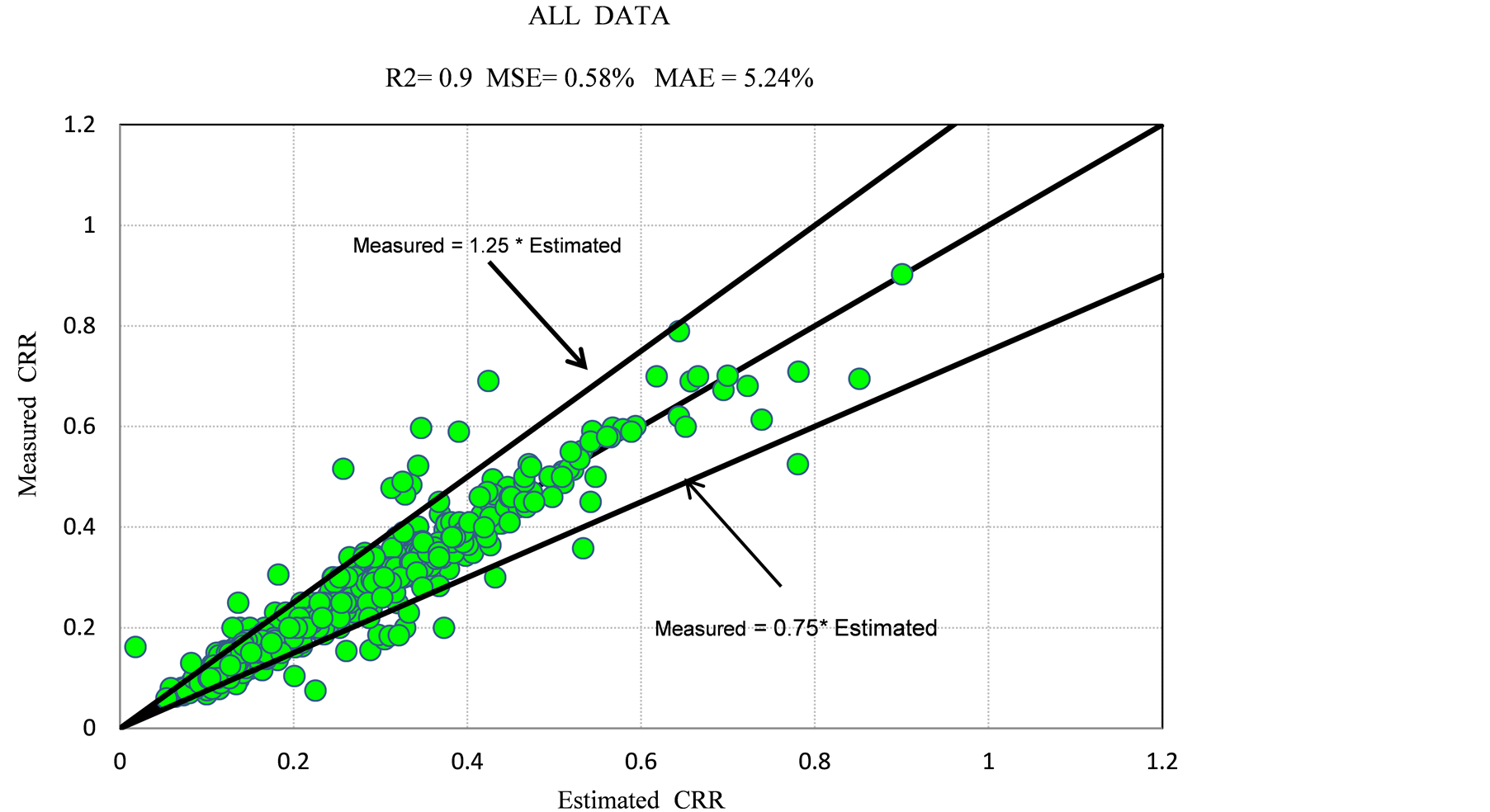
Figure 3. Predicted CRR by ANN model versus measured values for all element data.
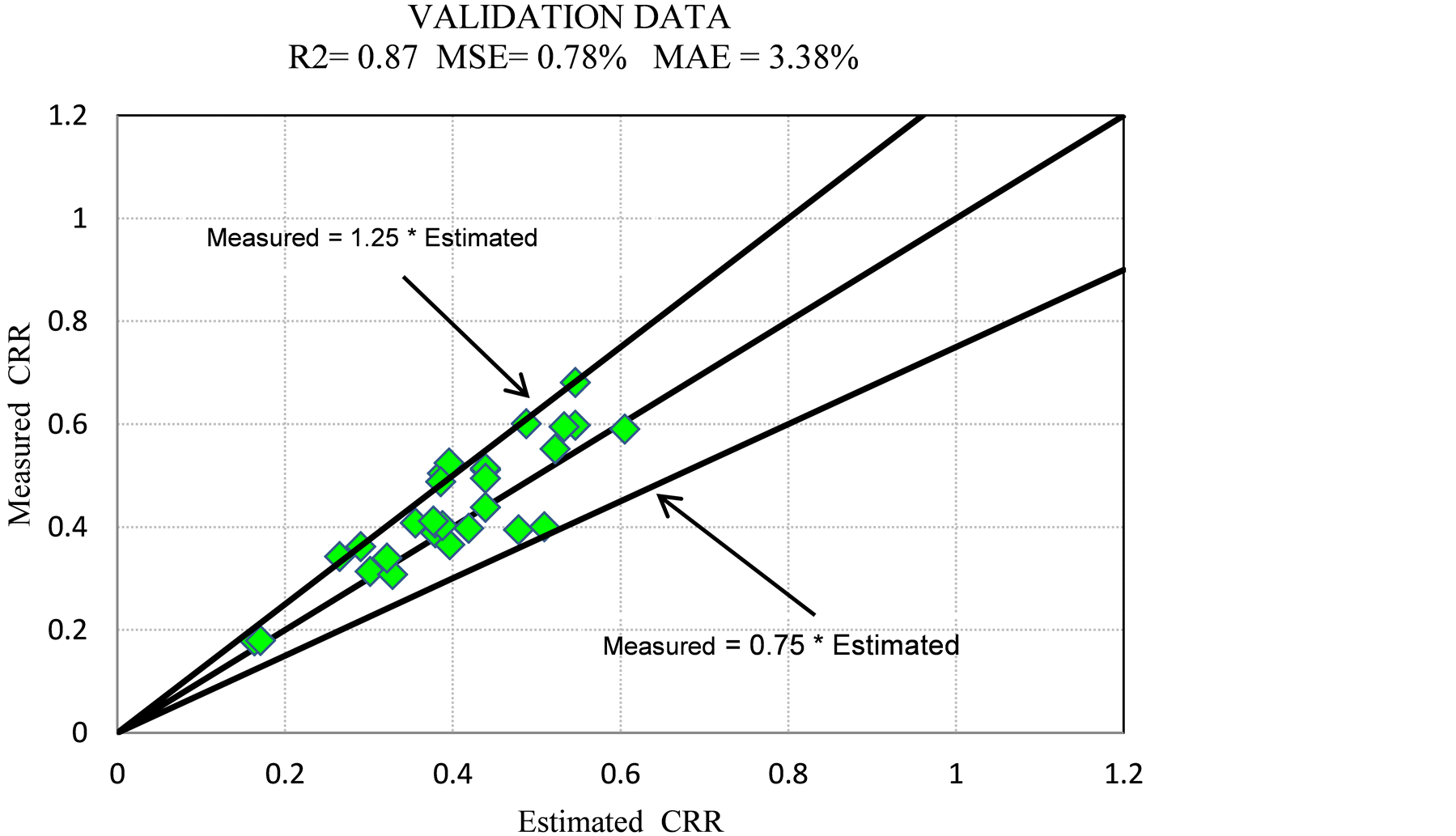
Figure 4. Predicted CRR by ANN model versus measured values for validation data element test.
sands deposits with silt content are much more susceptible to liquefaction than clean sand [15] [30] -[33] . However, there is no clear consensus in the literature about the effect of silt content increment on the trend of liquefaction resistance of sands. Some researchers [16] [32] [33] showed that for non-plastic FC increasing up to 35% and 44%, respectively, the liquefaction resistance of sand-silt mixtures with constant global void ratio decreases with respect to clean sand, whereas for FC greater than these values, the liquefaction resistance increases. Polito and Martin [33] [34] performed a laboratory parametric study utilizing cyclic triaxial tests to clarify the effects of non-plastic fines on the liquefaction susceptibility of sands. They found that liquefaction resistance for high FC is generally less than that of materials with low FC for a constant soil relative density which is consistent
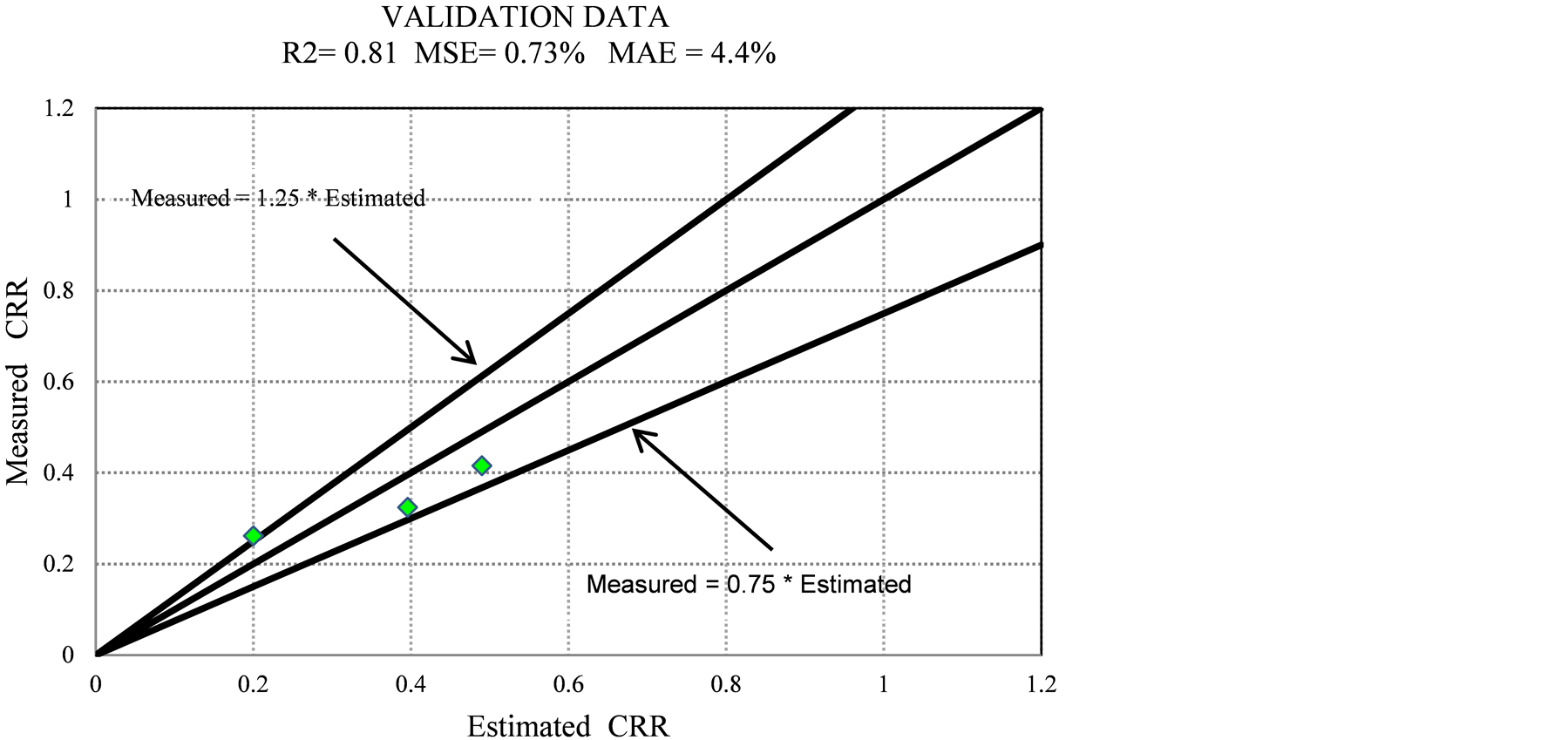
Figure 5. Predicted CRR by ANN model versus measured values for validation data centrifuge test.

Figure 6. Variations of cyclic stress ratio (CSR) by ANN model versus confining pressure, other parameters were kept constant at their average values.

Figure 7. Variations of cyclic stress ratio (CSR) by ANN model versus relative density (Dr%), other parameters were kept constant at their average values.
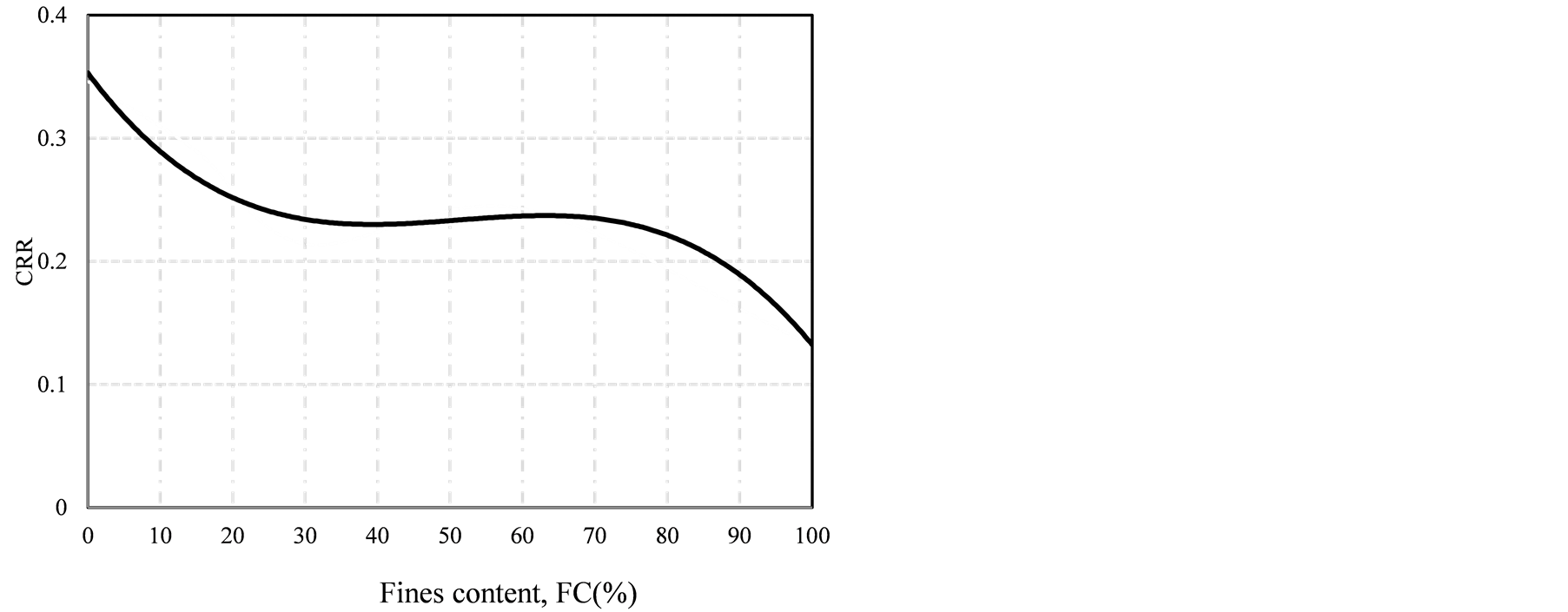
Figure 8. Variations of cyclic streesratio (CSR) by ANN model versus FC, other parameters were kept constant at their average values.

Figure 9. Effect of effective confining pressure on cyclic strength of sand (Amini and Qi 2000).

Figure 10. Effect of relative density on cyclic strength of sand (Hazirbaba 2006).
with the results of a study reported by others [31] -[34] . Figure 11 shows a plot of cyclic resistance versus silt content for specimens of Yatesville sand and silt presented by Polito and Martin [34] and Figure 12 shows Fines content effect versus cyclic resistance ratio (CRR) with constant relative density by Baziar and Sharafi [16] . The marked drop in cyclic resistance occurs as the silt content exceeds the 35% (almost 40%). The largest amount of silt that can be accommodated in the voids created by the sand skeleton is called the limiting silt content and occurs between 25% and 45% for most sands [16] [35] . In the present study, the results of analysis for the change in FC indicated that the liquefaction resistance of sand-silt deposits increased when FC increased up to about 30% and thereafter it started decreasing (Figure 8). A comparison between Figures 8-12 reveals that the same trend as reported by Polito and Martin, Baziar and Sharafi using cyclic triaxial tests and cyclic hollow torsiona test on silty sand specimens [15] [16] [33] [34] and prepared by moist tamping approach adjusted to 30% relative density, exists for ANN Model prediction. The agreement between the laboratory tests results and the prediction by the ANN model encourages the credibility of the proposed ANN Model.
6. Summary and Conclusions
In this paper, a database including 667 laboratory cyclic tests on clean and silty sands were utilized to develop an ANN model to predict the amount of cyclic resistance ratio. To determine suitable input parameters, five individual ANN models were constituted. Consequently, two of the better models were validated using centrifuge tests. Finally, a model with four input parameters (σ’ mean, Dr, FC, and Nl) and one hidden layer with 15 neurons was selected due to its good degree of accuracy and compatibility with basic understanding of liquefaction phenomenon. A parametric study was also conducted in this study using the proposed ANN model. The sensitivity of cyclic resistance ratio due to variation of soil initial parameters was evaluated. Results of parametric study illustrated that cyclic resistance ratio of sand-silt mixture continuously decreased with increasing σ'mean and also with increasing relative density (Dr). Also, it slightly increased when fines content (FC) increased up to about 40%, then decreased continuously while its decrement rate declined for greater fines content (FC). Results of this parametric study were confirmed with the results of experimental studies presented by other researchers. Upon analyzing the final model with all the data sets, the relative importance of each input variable was calculated using the approach suggested by Garson [36] . This method identifies the relative importance (or contribution) of each input variable towards the hidden-output connection weights of each hidden neuron. Incorporating input-hidden and hidden-output connection weights in that approach, relative importance values of input parameters were calculated. Table 4 shows the connection weights and relative importance of parameters for the proposed Model. From this table, the relative importance of initial mean effective stress, relative density, fines content (FC) and number of cycle (Nl) were obtained to be 17.93%, 30.36%, 32.76%, and 18.95%, respectively. Based on this result, it can be readily noted that the fines content (FC) has the most significant effect on the predicted CRR.

Figure 11. Effect of fines content on the liquefaction resistance of sandnonplastic fines mixtures for constant values of global void ratio and CSR = 0.23 (Xenaki and Athanasopoulos 2003).

Figure 12. Fines content effect versus cyclic resistance ratio (CRR) with constant relative density (Baziar and Sharafi, 2011).
Table 4. Connection weights and relative importance of soil capacity ANN Model 2 calculated via Garson (1991) technique.
The predicted CRR values using the new model for sands and silty sands were also in good agreement with those obtained from physical model tests, demonstrating that the model is capable of effectively capturing the liquefaction resistance features. The ANN model has yielded coefficients of determination (R2) equal to 0.9 for all element tests data and also validation tests data.
The input parameters of the model were categorized into three groups named as inter-granular contact density (σ'mean, Dr), fines content (FC), and cyclic loading (Nl). Total relative importance values for these three categories have been 48.29%, 32.76% and 18.95%, respectively. The results presented here showed the acceptable performance of ANN model in predicting cyclic resistant ratio values of a soil system to experience liquefaction triggering. Therefore it can be concluded that although, the ANN methods lack fundamental linkage with the soil response from a mechanistic point of view, the results presented here clearly demonstrated that the proposed ANN models are suitable to serve as a quick interpolating/extrapolating tool for understanding the relationship between CRR and the effective parameters for liquefaction assessment.
References
- Haykin, S. (1999) Neural Networks: A Comprehensive Foundation, Prentice-Hall, Englewood Cliffs, 161-187.
- Ali, H. and Najjar, Y. (1999) Neuronet-Based Approach for Assessing the Liquefaction Potential of Soils. Transportation Research Record 1633, Transportation Research Board, Washington DC, 3-8.
- Ghaboussi, J. (1992) Potential Applications of Neurobiological Computational Models in Geotechnical Engineering. In: Pande, G.N. and Pietruszezak, S., Eds., Numerical Models in Geotechnics, Rotterdam, The Netherlands, 543-555.
- Goh, A.T.C. (1996) Neural-Network Modeling of CPT Seismic Liquefaction Data. Journal of Geotechnical Engineering, 122, 70-73. http:///dx.doi.org/10.1061/(ASCE)0733-9410(1996)122:1(70)
- Kiefa, M.A.A. (1998) General Regression Neural Networks for Driven Piles in Cohesionless Soils. Journal of Geotechnical and Geoenvironmental Engineering, 124, 1177-1185. http:///dx.doi.org/10.1061/(ASCE)1090-0241(1998)124:12(1177)
- Kurup, P.U. and Dudani, N.K. (2002) Neural Networks for Profiling Stress History of Clays from PCPT Data. Journal of Geotechnical and Geoenvironmental Engineering, 128, 569-579. http:///dx.doi.org/10.1061/(ASCE)1090-0241(2002)128:7(569)
- Baziar, M.H. and Nilipour, N. (2003) Eval-uation of Liquefaction Potential Using Neural-Networks and CPT Results. Soil Dynamics and Earthquake Engineering, 23, 631-636. http:///dx.doi.org/10.1016/S0267-7261(03)00068-X
- Baziar, M.H. and Ghorbani, A. (2005) Evaluation of Lateral Spreading Using Artificial Neural Networks. Soil Dynamics and Earthquake Engineering, 25, 1-9. http:///dx.doi.org/10.1016/j.soildyn.2004.09.001
- Baziar, M.H. and Jafarian, Y. (2007) Assessment of Liquefaction Triggering Using Strain Energy Concept and ANN Model: Capacity Energy. Soil Dynamics and Earth-quake Engineering, 27, 1056-1072. http:///dx.doi.org/10.1016/j.soildyn.2007.03.007
- Juang, C.H., Yuan, H., Lee, D.-H. and Lin, P.-S. (2003) Simplified Cone Penetration Test-Based Method for Evaluating Liquefaction Resistance of Soils. Journal of Geotechnical and Geoenvironmental Engineering, 129, 66-80. http:///dx.doi.org/10.1061/(ASCE)1090-0241(2003)129:1(66)
- Rahman, M.S. and Wung, J. (2001) Lique-faction Prediction Using Fuzzy Neural Network Model Based on SPT. Proceedings of the 15th International Conference on Soil Mechanics and Geotechnical Engineering, Istanbul, 27-31 August 2001.
- Seed, H.B. and Idriss, I.M. (1971) Simplified Procedure for Evaluating Soil Liquefaction Potential. Journal of the Soil Mechanics and Foundations Division, 97, 1249-1273.
- Liang, L. (1995) Development of an Energy Method for Evaluating the Liquefaction Potential of a Soil Deposit. Ph.D. Dissertation, Department of Civil Engineering, Case Western Reserve University, Cleveland.
- Kim, Y.-S. and Kim, B.-T. (2006) Use of Artificial Neural Networks in the Prediction of Liquefaction Resistance of Sands. Journal of Geotechnical and Geoenvironmental Engineering, 132, 1502-1504. http:///dx.doi.org/10.1061/(ASCE)1090-0241(2006)132:11(1502)
- Sharafi, H. (2010) Evaluation of Lique-faction Potential and Earthquake-Induced Excess Pore Pressure in Silty Soils Using Energy Measures. Ph.D. Dissertation, School of Civil Engineering, Iran University of Science and Technology, Tehran.
- Baziar, M.H. and Sharafi, H. (2011) Assessment of Silty Sand Liquefaction Potential Using Hollow Torsional Tests— An Energy Approach. Soil Dynamics and Earthquake Engineering, 31, 857-865. http:///dx.doi.org/10.1016/j.soildyn.2010.12.014
- Baziar, M.H., Shahnazari, H. and Sharafi, H. (2011) A Laboratory Study on the Pore Pressure Generation Model for Firouzkooh Silty Sands Using Hollow Torsional Test. International Journal of Civil Engineering, 9, 126-134.
- Green, R.A. (2001) Energy-Based Evaluation and Re-mediation of Liquefiable Soils. Ph.D. Dissertation, Virginia Polytechnic Institute and State University, Black-sburg.
- Xenaki, V.C. and Athanasopoulos, G.A. (2003) Liquefaction Resistance of Sand-Silt Mixtures: An Expe-rimental Investigation of the Effect of Fines. Soil Dynamics and Earthquake Engineering, 23, 183-194. http:///dx.doi.org/10.1016/S0267-7261(02)00210-5
- Kanagalingam, T. (2006) Liquefaction Resistance of Granular Mixes Based on Contact Density and Energy Considerations. Ph.D. Dissertation, The State University of New York at Buffalo, Buffalo.
- Zhou, Y.-G. and Chen, Y.-M. (2007) Laboratory Investigation on Assessing Li-quefaction Resistance of Sandy Soils by Shear Wave Velocity. J Soil Dyn Earthquake Eng, 21.
- Houng, Y.-T., Huang, A.-B., Kuo, Y.-Ch. and Tsai, M.-D. (2004) A Laboratory Study on the Undrained Strength of a Silty Sand from Central Western Taiwan. Soil Dynamics and Earthquake Engineering, 24, 733-743. http:///dx.doi.org/10.1016/j.soildyn.2004.06.013
- Silver, M.L., Chan, C.K., Ladd, R.S., Lee, K.L., Tiedemann, D.A., Townsend, F.C., Valera, J.E. and Wilson, J.H. (1976) Cyclic Triaxial Strength of Standard Test Sand. Journal of the Geotechnical Engineering Division, 102, 511-523.
- Carraro, J.A.H., Bandini, P. and Salgado, R. (2003) Liquefaction Resistance of Clean and NonplasticSilty Sands Based on Cone Penetration Resistance. Journal of the Geotechnical Engineering Division, 129, 965-976. http:///dx.doi.org/10.1061/(ASCE)1090-0241(2003)129:11(965)
- Amini, F. and Qi, G.Z. (2000) Liquefaction Testing of Stratified Silty Sands. Journal of the Geotechnical Engineering Division, 126, 208-217. http:///dx.doi.org/10.1061/(ASCE)1090-0241(2000)126:3(208)
- Dief, H.M. (2000) Evaluating the Liquefac-tion Potential of Soils by the Energy Method in the Centrifuge. Ph.D. Dissertation, Department of Civil Engineering, Case Western Reserve University, Cleveland.
- Ishihara, K. and Yasuda, S. (1975) Sand Liquefaction in Hollow Cylinder Torsion under Irregular Excitation. Soils and Foundations, 15, 45-59. http:///dx.doi.org/10.3208/sandf1972.15.45
- Lade, P.V. and Yamamuro, J.A. (1997) Effects of Non-Plastic Fines on Static Liquefaction of Sands. Canadian Geotechnical Journal, 34, 918-928. http:///dx.doi.org/10.1139/t97-052
- Thevanayagam, S., Ravishankar, K. and Mohan, S. (1997) Effects of Fines on Monotonic Undrained Shear Strength of Sandy Soils. Geotechnical Testing Journal, 20, 394-406. http:///dx.doi.org/10.1520/GTJ10406J
- Thevanayagam, S. (1998) Effect of Fines and Confining Stress on Undrained Shear Strength of Silty Sands. Journal of the Geotechnical Engineering Division, 124, 479-491. http:///dx.doi.org/10.1061/(ASCE)1090-0241(1998)124:6(479)
- Koester, J.P. (1994) The Influence of Fine Type and Content on Cyclic Strength. Ground Failures under Seismic Conditions. Geotechnical Special Publication, No. 44, 330-345.
- Hazirbaba, K. (2005) Pore Pressure Generation Characteristics of Sands and Silty Sands: A Strain Approach. Ph.D. Thesis, University of Texas at Austin, Austin.
- Polito, C.P. (1999) The Effects of Non-Plastic and Plastic Fines on the Liquefaction of Sandy Soils. Ph.D. Thesis, Virginia Polytechnic Institute and State University, Blacksburg.
- Polito, C.P. and Martin II, J.R. (2001) Effects of Non-Plastic Fines on the Liquefaction Resistance of Sands. Journal of the Geotechnical Engineering Division, 127, 408-415. http:///dx.doi.org/10.1061/(ASCE)1090-0241(2001)127:5(408)
- Lee, K.L. and Seed, H.B. (1967) Cyclic Stress Conditions Causing Liquefaction of Sand. Journal of the Soil Mechanics and Foundations Division, 93, 47-70.
- Garson, G.D. (1991) Interpreting Neural Network Connection Weights. AI Expert, 6, 47-51.
NOTES
![]()
*Corresponding author.


