Modern Mechanical Engineering
Vol.4 No.2(2014), Article ID:46068,11 pages DOI:10.4236/mme.2014.42010
Semi-Analytical Approach for Stiffness Estimation of 3-DOF PKM
Hailemariam Nigus
Mechanical Engineering Department, Federal TVET Institute, Addis Ababa, Ethiopia
Email: hailuqua@gmail.com
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


Received 27 February 2014; revised 6 April 2014; accepted 18 April 2014
ABSTRACT
Due to their advantageous of high stiffness, high speed, large load carrying capacity and complicated surface processing ability, PKMs (Parallel Kinematic Manipulators) have been applied to machine tools. This paper mainly addresses the issue of stiffness formulation of a three-prismaticrevolute-spherical PKM (3-PRS PKM). The manipulators consist of three kinematic limbs of identical topology structure, and each limb is composed of an actuated prismatic-revolute-spherical. In order to build up the stiffness model, kinematics, Jacobian and finite element analysis are also performed as the basis. Main works in this paper can be outlined as follows. By use of approaches of vector, inverse position analysis of 3-PRS PKM is conducted. When the independent position and orientation parameters of the end-effectors are provided, the translational distances of active prismatic joints can be determined. Then with the aid of the wrench and reciprocal screw theory, the overall Jacobian of this manipulator is formulated quickly, and which is a six by six dimensional matrix and can reflect all information about actuation and constraint singularity. After formulating the position analysis and Jacobian matrix, the next step is stiffness analysis. Analytical stiffness model, a function of Jacobian matrix and components stiffness matrix, is obtained first using the principle of virtual work. Stiffness model is also a six by six dimensional matrix and can provide the information of actuation and constraint stiffness simultaneously. For the complex geometry shape of some components, it is impossible to know their stiffness distributions with the varying configuration. Therefore, ANSYS technology has to be applied to compute the stiffness coefficients of these components at different configurations. Then, the computed data are used to obtain the stiffness distribution by use of the numerical fitting method. Up to now, the semi-analytical stiffness model of the manipulator is completely formulated and can be applied to estimate the system stiffness of 3-PRS PKM. The model enables the stiffness of a 3-PRS PKM to be quickly estimated. Provided with the geometry parameters and load situation on tool tip, the stiffness of 3-PRS PKM system is estimated based on the stiffness matrix about tool tip which is obtained by transforming the point from the center of circle composed of three S joints to the tool tip. Then, the stiffness of system along x, y and z directions can be solved. In order to testify the correctness, the corresponding stiffness is also obtained by use of FEA software. The stress distribution and frequency of system are also gained by solving the FEA model.
Keywords:Parallel Kinematics Manipulator, Stiffness Analysis, FEA

1. Introduction
Stiffness is one of the most important performance indices of the PKMs, particularly for the use of high speed machining or heavy load assembling where high rigidity and dynamics are required. However, the complex geometry together with the changing rigidity of moving components throughout the whole workspace implies that to achieve a lightweight yet stiff design of PKMs is by no means an easy task. In the previous work dealing with stiffness analysis of PKMs, a great deal has been focused upon the formulation of the stiffness maps in the entire workspace by taking into account the limb rigidity [1] -[5] . By modeling a beam-like frame using FEA, a substructure-based modeling technique was proposed [6] [7] for quick stiffness estimation of a tripod PKM milling machine considering the rigidity of the machine frame.
The kinematic and static performances of the Tricept robot have been intensively investigated by Joshi and Tsai [8] by merely considering limb rigidity, in order to compare them with those of the 3-UPU parallel robot. Then a kinetostatic model for the Tricept is established by Zhang [9] based on lumped flexibilities theory, in order to account for joint and limb compliances.
2. Position Analysis
The schematic diagram of 3-PRS PKMs is showing in the Figure 1 below which is composed of moving platform, a fixed base and the three supporting limbs with identical configuration. Each limb connects the fixed base to the moving platform by prismatic, revolute and spherical joints in sequence and the prismatic joints are actuated by the linear actuator. The considered machine is a 3-DOF PKM a reference frame R is attached to the base and a body fixed frame R0 to the plate form with O and Oo located at the center of the equilateral triangle 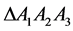 and
and 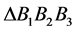 as shown.
as shown.
The Z and Z0 axes are normal to the planes of those triangles. The x axis is parallel to 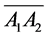 and the
and the 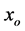 axis is parallel to
axis is parallel to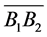 . Also an instantaneous reference frame Ro is set which its origin at point Oo and its three orthogonal axes remaining always parallel to those of R. Consequently the orientation matrix of R0 with respect to R can be obtained using three Euler angles
. Also an instantaneous reference frame Ro is set which its origin at point Oo and its three orthogonal axes remaining always parallel to those of R. Consequently the orientation matrix of R0 with respect to R can be obtained using three Euler angles 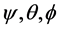 in terms of precession nutation and body rotation according to the Z-X-Z convention.
in terms of precession nutation and body rotation according to the Z-X-Z convention.
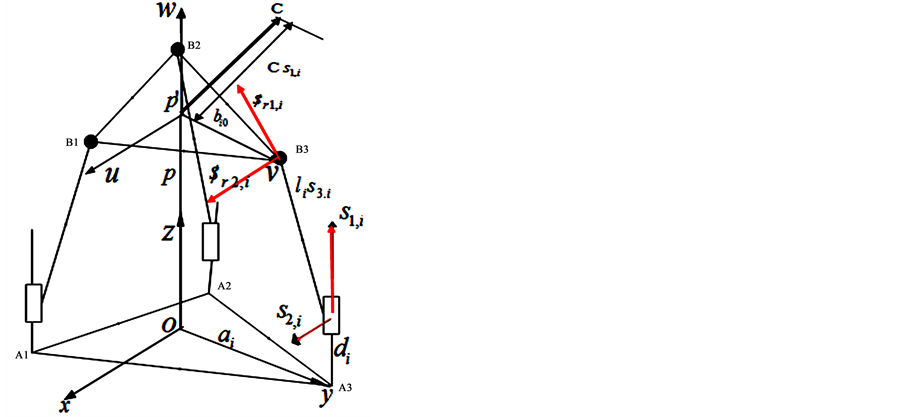
Figure 1. Schematic diagram of 3-PRS PKM.
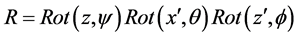 ,
, 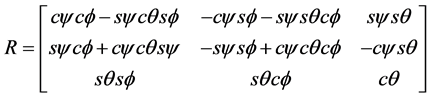
where s ans c represents “sin” and “cos” respectively. The position vector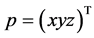 , of p can be expressed as
, of p can be expressed as
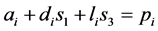 (1)
(1)
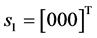 ,
, 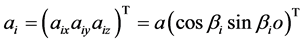
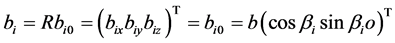
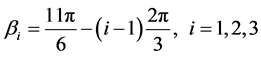
The constraint imposed by the revolute joint restricts the translational motion of revolute joint in the limb
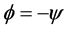 ,
, 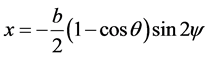 ,
, 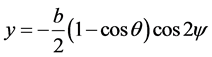 ,
,
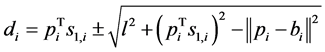 (2)
(2)
3. Jacobian Analysis
The theory of reciprocal screw in an effective way to drive the Jacobian matrix of parallel manipulator; with 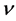 and
and 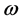 respectively denoting the vectors for the linear and angular velocities, the twist of the Mobil plat form can be defined as,
respectively denoting the vectors for the linear and angular velocities, the twist of the Mobil plat form can be defined as,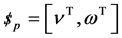 .
.
A linear actuator drives each of prismatic joint. The connectivity of each limb is equals to five. Therefore the instantaneous twist 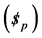 of the moving platform can be expressed as a linear combination of five instantaneous twist as follows.
of the moving platform can be expressed as a linear combination of five instantaneous twist as follows.
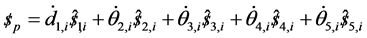 (3)
(3)
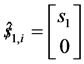 ,
, 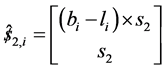 ,
, 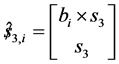 ,
, 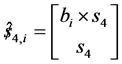 ,
, 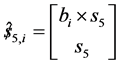
where 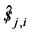 a unit vector along the jth joint axes of the ith limb. Those screw that are reciprocal to all the joint screws of the ith limb of the 3-PRS parallel kinematic manipulator form a 1-system. Hence one screw is reciprocal to all the joint screw of the limb can be identified. This reciprocal screw denoted as
a unit vector along the jth joint axes of the ith limb. Those screw that are reciprocal to all the joint screws of the ith limb of the 3-PRS parallel kinematic manipulator form a 1-system. Hence one screw is reciprocal to all the joint screw of the limb can be identified. This reciprocal screw denoted as 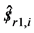 is zero pitch screw passing through the center of spherical joint and parallel to
is zero pitch screw passing through the center of spherical joint and parallel to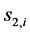 .
.
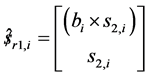 (4)
(4)
By taking the inner product (orthogonal product) of both sides of the instantaneous twist Equation (3).
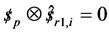
Writing the equation once for each limb produce 3 equations which can be written in matrix form.

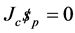
Since this constraint wrench is reciprocal to all screw the right side equation of twist screw will be zero.
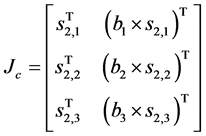 (5)
(5)
Next we look the prismatic joint in each limb with actuator locked, the reciprocal screw for each limb form a two system. An additional basis screw which is reciprocal to the passive joints of the ith limb can be identified as zero pitch screw passing through the center of spherical joint. This reciprocal screw represent wrench of actuation and it’s normal to the pervious one system. That is
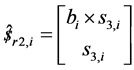
Take the orthogonal product of this reciprocal wrench for both side of the twist screw 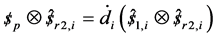 this can be re write again
this can be re write again
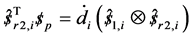
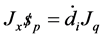
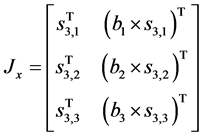 (6)
(6)
And we can find 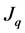 by orthogonal product of the right side of the above equation
by orthogonal product of the right side of the above equation
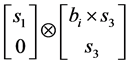
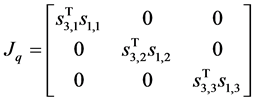
Since this machine is not outer driving manipulator 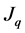 will not be identity matrix. Then to fond the actuation Jacobian
will not be identity matrix. Then to fond the actuation Jacobian
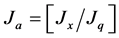 (7)
(7)
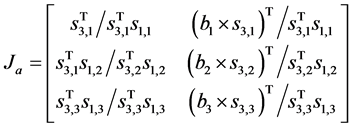
To find the overall Jacobian matrix by composing the actuation matrix in and constrained matrix on 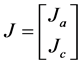
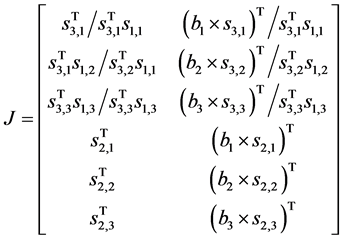
4. Stiffness Modeling
4.1. Stiffness Equations
Under the assumption that the platform and the machine frame are rigid, when the platform is subjected to the external wrench 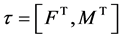 on the reference point p, where
on the reference point p, where 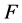 and
and 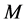 are the external force and torque applied to the platform, the deformation of the limbs will causes the platform to experience a twist
are the external force and torque applied to the platform, the deformation of the limbs will causes the platform to experience a twist 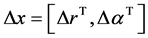 in terms of the translational and rotational deformations along/about the axes of frame.
in terms of the translational and rotational deformations along/about the axes of frame.
Then, applying the virtual work principle to the platform gives
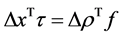 (8)
(8)
where 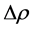 and
and  represents the set of deflections and reaction force magnitude
represents the set of deflections and reaction force magnitude
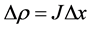
This equation 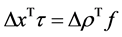 can be re write
can be re write 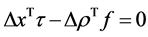 Substitute
Substitute 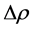 from the above equation
from the above equation
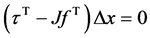
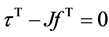
Taking the transpose yields:
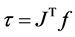
where 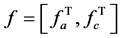 is the internal wrench vector of limbs, where
is the internal wrench vector of limbs, where 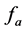 and
and 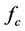 are the generalized force of the PRS limbs and the PR limb related to the twist
are the generalized force of the PRS limbs and the PR limb related to the twist 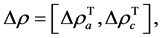
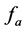 is a force which is parallel to the screw axis while the
is a force which is parallel to the screw axis while the 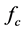 is parallel to the revolute axis.
is parallel to the revolute axis.
Therefore the virtual work principle can be written
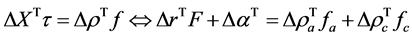
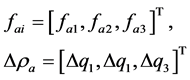
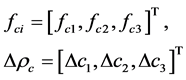 (9)
(9)
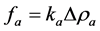 ,
, 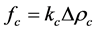 and
and 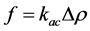
where .
.
Here 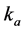 and
and 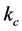 are known as the component stiffness matrix of actuation and constraints respectively the formulation of their element
are known as the component stiffness matrix of actuation and constraints respectively the formulation of their element
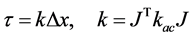 (10)
(10)
And the compliance model can be evaluated as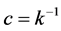 .
.
4.2. Formulation of 
As shown in the Figure 2 above the limb model has to formulate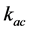 . I group all the parts of a PRS limp in to four components: 1) the spherical joint; 2) the limp body which is the fixed lengths link; 3) R joint assembly; 4) the lead screw assembly. As well as analytically convenient, they are sub systems that must realistically be subjected independently to design improvements.
. I group all the parts of a PRS limp in to four components: 1) the spherical joint; 2) the limp body which is the fixed lengths link; 3) R joint assembly; 4) the lead screw assembly. As well as analytically convenient, they are sub systems that must realistically be subjected independently to design improvements.
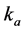 is given in a diagonal matrix i.e.
is given in a diagonal matrix i.e. 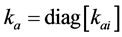 where
where  with
with  being the axial stiffness
being the axial stiffness
Figure 2. A limb model for stiffness evaluation.
coefficient at 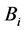 along the
along the 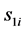 axis of the ith limb referring to the Figure 3.
axis of the ith limb referring to the Figure 3. 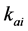 can be modeled by four serially connected springs each representing the stiffness of one of the four components such
can be modeled by four serially connected springs each representing the stiffness of one of the four components such
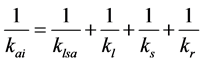 (11)
(11)
where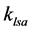 ,
, 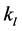 ,
, 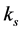 and
and 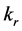 are the axial stiff nesses coefficients of the lead screw assembly, the fixed length limb, S joint and R joint assembly respectively.
are the axial stiff nesses coefficients of the lead screw assembly, the fixed length limb, S joint and R joint assembly respectively.
Note that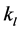 , and
, and 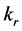 are constant and can be evaluated using finite element analysis. (FEA) by the ANSYS workbench which is very convenient to analysis a solid model like PKM.
are constant and can be evaluated using finite element analysis. (FEA) by the ANSYS workbench which is very convenient to analysis a solid model like PKM.
The 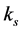 varies with the configuration and should be evaluated as in the local frame since the spherical actuation is parallel to w, the coefficient stuffiness is calculated as follows
varies with the configuration and should be evaluated as in the local frame since the spherical actuation is parallel to w, the coefficient stuffiness is calculated as follows
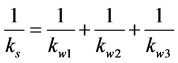 (12)
(12)
The values of Equation (12) can be substituted from Table 1 below.
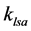 is the lead screw assembly the combination of serially connected springs such as
is the lead screw assembly the combination of serially connected springs such as
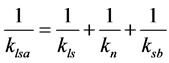 (13)
(13)
where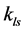 ,
, 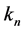 and
and 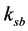 are the stiffness coefficients of lead screw nut and support bearings respectively.
are the stiffness coefficients of lead screw nut and support bearings respectively. 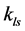 is the lead screw which is the linear function of the limb length and can be defined as
is the lead screw which is the linear function of the limb length and can be defined as
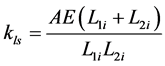 (14)
(14)
where 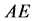 stands for cross sectional area of the lead screw and Yang’s modular respectively
stands for cross sectional area of the lead screw and Yang’s modular respectively 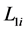 and
and 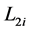 are the distance b/n the nut and the supporting bearing located at both ends.
are the distance b/n the nut and the supporting bearing located at both ends.
To find the constrained coefficient of stiffness matrix we can find as the same fashion of finding the actuation coefficient matrix. Similarly
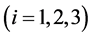
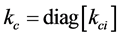
where 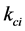 is the bending stiffness coefficient at the platform along the
is the bending stiffness coefficient at the platform along the 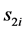 axis of the
axis of the 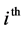 limb. Then
limb. Then 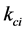 can be evaluated by taking reciprocal sum of the bending stiffness coefficient of the fixed length limb, S joint and R joint assembly respectively.
can be evaluated by taking reciprocal sum of the bending stiffness coefficient of the fixed length limb, S joint and R joint assembly respectively.
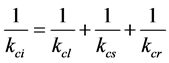 (15)
(15)
Again the 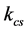 can be evaluated by the configuration and should be evaluated as in the local frame since the spherical parallel to the constraint is to u the coefficient stuffiness is calculated as follows
can be evaluated by the configuration and should be evaluated as in the local frame since the spherical parallel to the constraint is to u the coefficient stuffiness is calculated as follows
Table 1. The stiffness coefficient of the S joint.
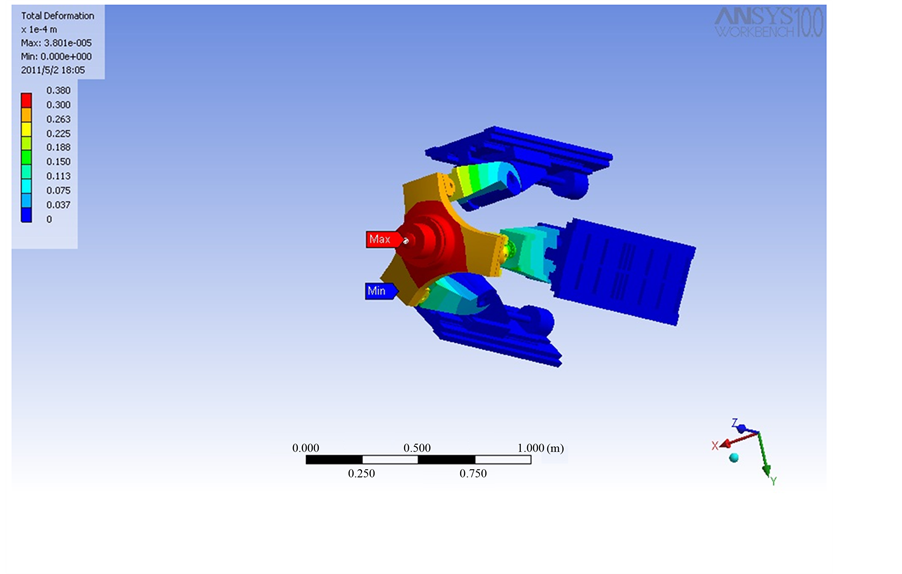
Figure 3. Deformation with 1 KN force imposed at the spindle along y-axis.
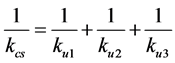 (16)
(16)
The value of the stiffness will be substitute from Table 1 and easy to compute the value of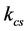 . The
. The 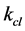 and
and 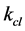 can be computed easy by FEA. Using the software ANSYS workbench by applying a 1 KN force on the spherical joint which is parallel to the
can be computed easy by FEA. Using the software ANSYS workbench by applying a 1 KN force on the spherical joint which is parallel to the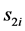 .
.
4.3. Formulation of Overall Stiffness Matrix on Tool Tip
Formulation of overall stiffness matrix applied on the center of end-effectors is calculated on Equation (15) which is
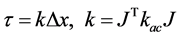
To find the overall coefficient of stuffiness matrix on tool tip it needs to transform the Equation (10) in to tool tip by the transformation matrix
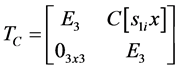 (17)
(17)
If let  be imposed at the tool tip
be imposed at the tool tip  and
and 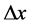 be the corresponding small deflection twist the overall stiffness matrix about point
be the corresponding small deflection twist the overall stiffness matrix about point 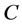 can easily be developed by replacing
can easily be developed by replacing 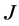 in Equation (10) with
in Equation (10) with 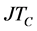 that is
that is
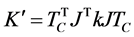
where 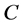 is the distance from p to
is the distance from p to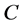 ,
, 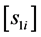 denotes the screw matrix of
denotes the screw matrix of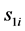 , and
, and 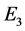 denotes a unit matrix of order 3.
denotes a unit matrix of order 3.
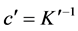
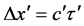
where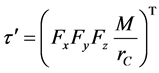 .
.
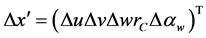
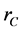 is the maximum radius of the cutting tool specified by the spindle head.
is the maximum radius of the cutting tool specified by the spindle head.
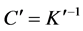
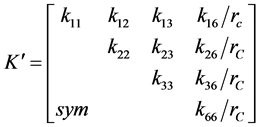 (18)
(18)
In order to evaluate the rigidity of a system we define the rigidity along/about three orthogonal axis of the frame 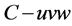 by the diagonal corresponding element of C.
by the diagonal corresponding element of C.
 ,
,  ,
, 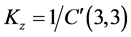 ,
, 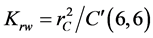 ,
,
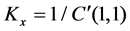 ,
, 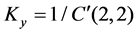 ,
, 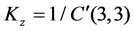 ,
,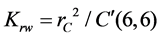 .
.
5. Stiffness Analysis
The stiffness of the 3-PRS PKM is evaluated in the decomposing the machine in to limbs and apply a force on the spherical joint to find the actuated and constraint coefficient of stuffiness. With the aid of finite element analysis and numerical evaluated both actuated and constraint stiffness of the limb assembly is evaluated. The overall stiffness of the manipulator on the center of the plate form will be calculated as in Equation (10) indicated. Since in real sense the force/moment is applied on the too tip of the machine, it needs transform the stiffness matrix gained in Equation (10) to the tool tip by the transform matrix Equation (16) it gives a stiffness coefficient matrix on tool tip as shown in the Equation (18). Then diagonal values in the stiffness matrix indicates the overall stiffness of the machine when force applied along x, y and z which explain in detail. In order to evaluate the rigidity of a system we define the rigidity along/about three orthogonal axis of the frame 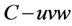 by the diagonal corresponding element of C.
by the diagonal corresponding element of C.
 ,
, 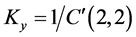 ,
, 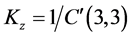 ,
,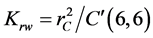 .
.
Comparison with FEA Results
According to the above analysis, the detailed design was carried out and the stiffness of the virtual prototype was evaluated by ANSYS at four typical positions as shown from Figures 3-6 with 1 KN force is applied at the tool tip along x, y and z and moment about z axis respectively. I can get the deformation easily from the FEA and the stiffness can get by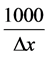 . It can been seen from Table 2 that the estimated results of the mathematical models developed have a good match with those obtained by the FEA in terms of magnitude and distribution as well.
. It can been seen from Table 2 that the estimated results of the mathematical models developed have a good match with those obtained by the FEA in terms of magnitude and distribution as well.
The estimated linear stiffness along three orthogonal axis and the torsion stiffness about the w-axis of the 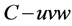 frame, it can be seen that the stiffness distribution are tri-symmetrical in nature and the
frame, it can be seen that the stiffness distribution are tri-symmetrical in nature and the 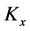 and
and 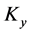 are similar in magnitude.
are similar in magnitude.
6. Conclusions
The modeling methodology for the semi-analytical stiffness estimation of a 3-PRS parallel kinematic manipulator
Table 2. Results obtained by the semi-analytical method and by FEA.

Figure 4. Deformation with 1 KN force imposed at the spindle along x-axis.

Figure 5. Deformation with 1 KN force imposed at the spindle along z-axis.
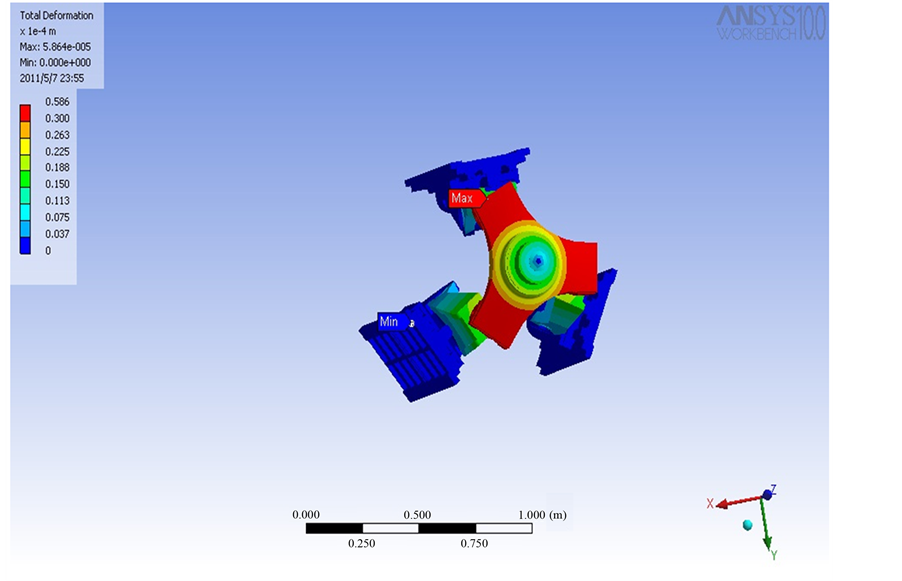
Figure 6. Deformation with 1 KN force imposed at the spindle moment about z.
has been systematically investigated by considering rigidity of the machine frame. The conclusions are drawn as follows:
1) The 6 × 6 Jacobian matrix consists of two sub matrices: one associated with the constraints imposed by the joints and the other associated with the actuation effects.
2) The stiffness model of machine as a whole can be generated mathematical model formulated in the conceptual design.
3) By the use of FEA with the tool of ANSYS work bench, I analyzed the machine stiffness and compared the FEA result with the semi-analytical analysis and the estimated stiffness results have a good match with those obtained by the FEA, thereby supporting the validity of this approach.
References
- Gosselin, C.M. (1990) Stiffness Mapping for Parallel Manipulators. IEEE Transactions on Robotics and Automation, 6, 377-382. http://dx.doi.org/10.1109/70.56657
- Clinton, C.M. and Zhang, G. (1997) Stiffness Modeling of a Stewart-Platform-Based Milling Machine. Transaction of NAMRI/SME, 115, 335-340.
- El-Khasawneh, B.S. and Ferreira, P.M. (1999) Computation of Stiffness and Stiffness Bounds for Parallel Link Manipulators. International Journal of Machine Tools and Manufacture, 39, 321-342. http://dx.doi.org/10.1016/S0890-6955(98)00039-X
- Kim, J., Park, F.C., Ryu, S.J., Hwang, J.C., Park, C. and Iurascu, C.C. (2001) Design and Analysis of a Redundantly Actuated Parallel Mechanism for Rapid Machining. IEEE Transactions on Robotics and Automation, 17, 423-434. http://dx.doi.org/10.1109/70.954755
- Goldsmith, P.B. (2003) Design and Kinematics of a Three-Legged Parallel Manipulator. IEEE Transactions of Robotics and Automation, 19, 726-731. http://dx.doi.org/10.1109/TRA.2003.814508
- Huang, T., Zhao, X.Y. and Whitehouse, D.J. (2002) Stiffness Estimation of a Tripod-Based Parallel Kinematic Machine. IEEE Transactions of Robotics and Automation, 18, 50-58. http://dx.doi.org/10.1109/70.988974
- Huang, T., Mei, J.P., Zhao, X.Y., Zhou, L.H., Zhang, D.W. and Zeng, Z.P. (2001) Stiffness Estimation of a TripodBased Parallel Kinematic Machine. Proceeding of the IEEE International Conference on Robotics & Automation, 4, 3280-3285.
- Joshi, S. and Tsai, L.W. (2003) A Comparison Study of Two 3-DOF Parallel Manipulators: One with Three and the Other with Four Supporting Legs. IEEE Transactions on Robotics and Automation, 19, 200-209. http://dx.doi.org/10.1109/TRA.2003.808857
- Zhang, D. and Gosselin, C.M. (2001) Kinetostatic Modeling of N-DOF Parallel Mechanisms with a Passive Constraining Leg and Prismatic Actuators. ASME Journal of Mechanical Design, 123, 375-384. http://dx.doi.org/10.1115/1.1370976


