Modern Mechanical Engineering
Vol.4 No.1(2014), Article ID:43266,7 pages
DOI:10.4236/mme.2014.41004
Controlled Cooling of Hot Rolled Steel Channels by Water Spraying on the Final Cooling Bed
1Ford Motor Car Company, Dearborn, USA
2Department of Mechanical Engineering, Lamar University, Beaumont, USA
Email: malur.srinivasan@lamar.edu
Copyright © 2013 Abraham Yik-Sau Tang. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received December 16, 2013; revised January 18, 2014; accepted January 29, 2014
Keywords: Finite Element Method; Steel Channel; Water Spray Cooling; Microstructure; Nonequilibrium Cooling
ABSTRACT
The objective of this research is to design an effective and relatively simple method for controlled cooling of hot rolled steel channels by water spraying on the final cooling bed after continuous cast steel billets passing through reheating furnace and sequential rolls to form channels. The need for this research arose as the channels were being cooled by forced air draft and natural convection which brought the temperature of the channels to about 270C (518F) at the shear stand. Steel at this temperature is too hot for convenient handling by the operators. Additional cooling by water spraying would be an acceptable solution but such cooling should be designed to enable an acceptable microstructure to be developed in the channel, as the microstructure of steel is strongly affected by nonequilibrium cooling through the eutectoid range: the mechanical properties of steel are a conse-quence of the microstructure. The approach followed in this investigation was first to develop a finite element method (FEM) to determine the temperature profiles in the channel subjected to cooling by water spraying and natural convection and arrive at suitable water spray rates to bring the temperature of the channel at the shear stand to levels suitable for convenient handling. PATRAN was used for preprocessing and ABAQUS for pro- cessing and post processing. Next, laboratory experiments were conducted to determine the microstructure and hardness of channels at the spray rates found suitable through FEM, to suggest the water spray rate most suitable for providing a temperature convenient for handling and for developing a desirable microstructure.
1. Introduction
Hot rolled steel channels conforming to ASTM A36 are used for general structural proposes in buildings, bridges, machinery and others [1]. The specified chemical composition is in the range: carbon—0.18 - 0.24 wt.%, silicon—0.1 wt.%, manganese—0.3 - 0.6 wt.%, phosphorus —0.035 wt.%, sulfur—0.035 wt.% and iron—balance. In mini-steel mills, hot metal melted in an electric arc furnace is poured into a continuous casting machine to produce (usually) square billets. These billets are reheated in a resistance furnace and rolled in successive steps into the final desired shape, which in the present study is a channel. The final product is cooled on a bed before being cut into desired lengths prior to any straightening and transported to the shipping zone. The cooling of the deforming billet in the rolling stands is usually standardized, but is not so rigorously controlled on the cooling bed in many small mills. The cooling rate at this stage, however, has important production, handling and microstructure (and hence, mechanical properties) consequences. Cooling too slow in a reasonable period of time may make the temperature at the cutting stand too high to handle; increasing the cooling time at slow rates produces undesirable microstructure. In high-end steel mills, specially designed and usually patented units are installed for controlled cooling rate. In the steel mill the authors visitedno such unit was installed, and the authors decided to design a simple and effective cooling unit that would not only provide channels at a convenient temperature for handling at the cutting stand, but also provide a good microstructure (and hence mechanical behavior) consistent with ASTM A-36 specification. The design involved finite element modeling of the cooling of the channel using water spray under the cooling bed that resulted in acceptable handling temperatures and the fabrication of the setup and experimentation with actual water spray to study the variation of microstructure and hardness at the designed water spray rates, so as to arrive at an appropriate water spray rate. The results of this work are presented and discussed in this paper.
2. Finite Element Modeling (FEM)
FEM used in the present work involved the following steps: a) preprocessing of the cross section of a channel using PATRAN, b) solution (processing) of heat transfer from the cross section of a channel using ABAQUS and c) postprocessing using ABAQUS. In Figure 1 is shown a schematic diagram of the channel considered in the present work. The full details of the preprocessing mesh generation and transfer to ABAQUS are available in the Master of Science thesis by Rachamadugu [1].
The processing using ABAQUS involved the solution of two-dimensional transient heat conduction equation subjected to the applicable initial and boundary conditions. The relevant equation is
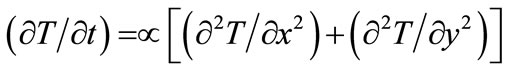 (1)
(1)
where, T is the temperature, t is the time, x and y are the Cartesian spatial coordinates
in the channel. , in which α is thermal diffusivity, k is the thermal
conductivity of steel, ρ is the density of steel and c is the specific heat of steel.
The initial condition is T = 1650˚F (899˚C) at t = 0 at x ≥ 0 and y ≥
0. The boundary conditions are established based on the conditions at the steel
plant and the main object of this investigation. The cooling of the channel is by
conduction inside the body of the channel and by convection and radiation from the
surfaces. The estimation of the heat transfer coefficients is based on the following
considerations.
, in which α is thermal diffusivity, k is the thermal
conductivity of steel, ρ is the density of steel and c is the specific heat of steel.
The initial condition is T = 1650˚F (899˚C) at t = 0 at x ≥ 0 and y ≥
0. The boundary conditions are established based on the conditions at the steel
plant and the main object of this investigation. The cooling of the channel is by
conduction inside the body of the channel and by convection and radiation from the
surfaces. The estimation of the heat transfer coefficients is based on the following
considerations.
1) The channel is placed on the rollers of cooling bed with its flat face downwards and the flanges face vertically upwards.
2) The free convective heat transfer coefficient for the flat face is calculated
from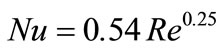 , for 26,000 < Re < 107, where, Re is the Rayleigh
number given by Re = Gr. Pr, in which Gr is the Grashof number and Pr is the Prandtl
number. Prandtl number is given by
, for 26,000 < Re < 107, where, Re is the Rayleigh
number given by Re = Gr. Pr, in which Gr is the Grashof number and Pr is the Prandtl
number. Prandtl number is given by
 where µ is the absolute viscosity of the convective medium. Also,
where µ is the absolute viscosity of the convective medium. Also,
 ,
where β is inverse of the ambient temperature, Δt is the temperature difference
between the channel flat face and the ambient temperature and ν is the kinematic
viscosity of the convective medium. Nu is the Nusselt number for a flat face of
the channel of length L and is given by Nu = hL/k in which h is the free convective
heat transfer coefficient [2,3].
,
where β is inverse of the ambient temperature, Δt is the temperature difference
between the channel flat face and the ambient temperature and ν is the kinematic
viscosity of the convective medium. Nu is the Nusselt number for a flat face of
the channel of length L and is given by Nu = hL/k in which h is the free convective
heat transfer coefficient [2,3].
3) The free convective heat transfer coefficient for the flanges is calculated using [4,5].
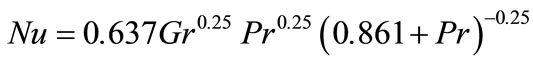 considering
the flange height h (2.7 inches or 68.6 mm) instead of the flat face length L (taken
as 48 inches or 1219 mm) for Grashof number calculation.
considering
the flange height h (2.7 inches or 68.6 mm) instead of the flat face length L (taken
as 48 inches or 1219 mm) for Grashof number calculation.
4) A target temperature of 250˚F (~120˚C) or less should be achievable in about 4 minutes or less, from the time of entry of the channel on the cooling bed and this is achieved by suitably designed water spray system. The
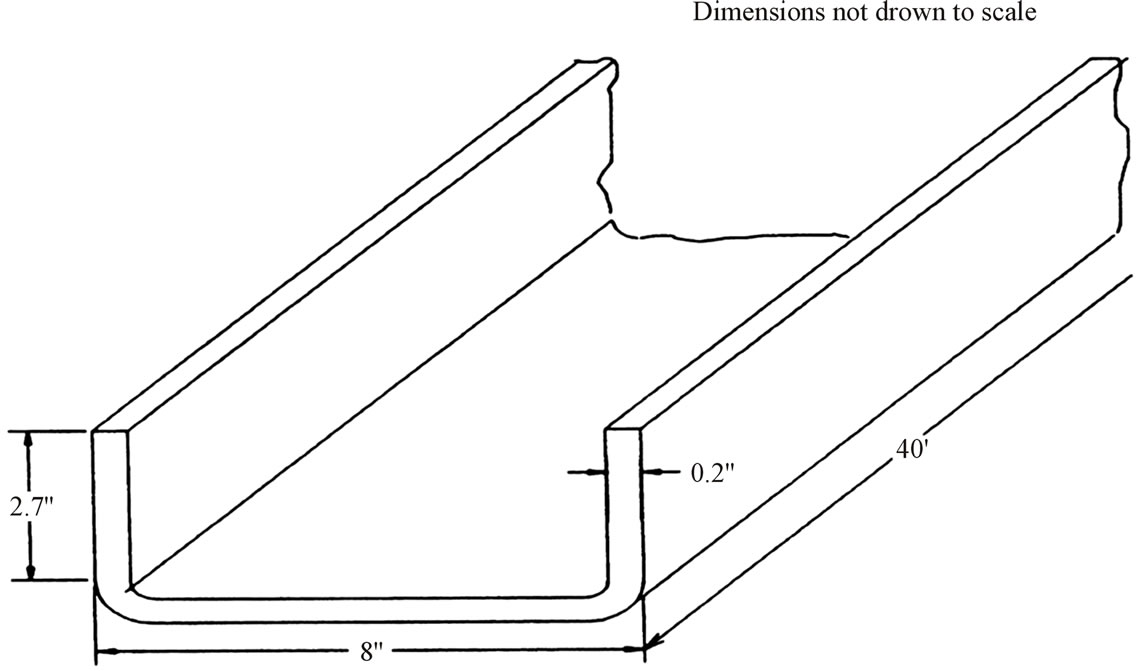
Figure 1. ASTM A-36 Channel Dimensions are shown in inches and feet (1 inch = 25.4 mm, 1 foot = 304.8 mm or ~0.3 m).
heat transfer coefficient of the water spray is calculated by an iterative process on ABAQUS. This also incorporates the radiative heat transfer coefficient and the heat transfer coefficient at film boiling stage. The overall heat transfer coefficient is determined from steps (b), (c) and (d) and applied to the surfaces as appropriate.
Processing was done using ABAQUS that makes use of backward difference operator or modified Crank-Nicholson method to integrate the partial differential equation. This scheme is considered to be unconditionally stable for linear problems. Four-noded linear interpolation elements (DCAX4) were used for the transient heat conduction analysis. The integration points, being located at the nodal points greatly improved the accuracy of computation. The time-step for temperature calculation was based in the criterion
 ,
where
,
where
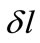 is the element length and
is the element length and
 is the time step, the other symbols being as defined earlier. As per this criterion
a time-step of 3 seconds was used in the present work. The thermal and physical
properties assumed for steel and air (convecting medium) were as follows: density
of steel = 0.284 lb./in3 (7861 kg/ m3), thermal conductivity
of steel = 0.03597 Btu/min. in. ˚F (0.06 W/m K), specific heat of steel = 0.1592
Btu/lb. ˚F (666 J/kg K), density of air = 0.000044396 lb./in3 (1.22
kg/m3), thermal conductivity of air = 0.00064456 Btu/min·in. ˚F
(0.0011 W/m. ˚K), specific heat of air = 0.237 Btu/lb. ˚F (99 J/kg. ˚K).
is the time step, the other symbols being as defined earlier. As per this criterion
a time-step of 3 seconds was used in the present work. The thermal and physical
properties assumed for steel and air (convecting medium) were as follows: density
of steel = 0.284 lb./in3 (7861 kg/ m3), thermal conductivity
of steel = 0.03597 Btu/min. in. ˚F (0.06 W/m K), specific heat of steel = 0.1592
Btu/lb. ˚F (666 J/kg K), density of air = 0.000044396 lb./in3 (1.22
kg/m3), thermal conductivity of air = 0.00064456 Btu/min·in. ˚F
(0.0011 W/m. ˚K), specific heat of air = 0.237 Btu/lb. ˚F (99 J/kg. ˚K).
While the above procedure enables the determination of temperature variation with time on the cooling bed, from the design view point it is necessary to determine the water spray rate from each nozzle and the number of nozzles. As per existing conditions at the plant the length of each channel bed was 40 feet (12.19 m) and therefore it was assumed that 10 nozzles, each covering a distance of 4 feet (~1.22 m) would serve the purpose. The water spray density for each nozzle can be calculated from [6]
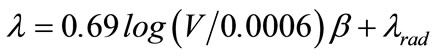 (2)
(2)
where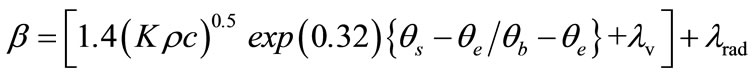
λ = heat transfer coefficient of water spray V = spray water density k = thermal conductivity of steel
ρ = density of steel c = specific heat of steel
θs = surface temperature of steel
θb = temperature of cooling water
θc = evaporation temperature of cooling water
λv = heat transfer coefficient at film boiling stage
λrad = radiative heat transfer coefficient, determined using Stefan-Boltzmann constant, surface temperature, ambient temperature and emissivity constant.
3. Experimental Work
The object of the experimental work was to subject actual channels to cooling rates estimated to be appropriate to result in the chosen exit temperature on the cooling bed at the cutting stand after water spraying and study the microstructure and hardness of the channel obtained. For this purpose a water spray unit was designed by modifying an existing Jominy end quench apparatus so that a channel of length 12 inches (~0.3 m) could be placed horizontally above the water spray nozzle at a distance about 12 inches (~0.3 m), with the flat face of the channel facing the nozzle. A thermocouple was attached to the channel above the nozzle on the face away from the spray zone and the temperature variation with time was continuously recorded in a strip chart recorder. The water spray knob was calibrated to provide the desired spray rate at chosen positions of the knob. The channel was heated in an argon atmosphere furnace to a temperature of 1650˚F, held for 30 minutes, quickly placed the spray stand and subjected to water spray for about 4 minutes, while simultaneously recording the temperature variation with time. The channel was air cooled to room temperature after spraying and a specimen of approximately 12 mm square was cut from the channel at the center of the spray zone. The specimen was then subjected to standard metallographic grinding and polishing for hardness and microstructure examination. The etchant used was 2% solution of nitric acid in alcohol, after the hardness measurement was made using a Brinell hardness tester with a 10 mm ball and 3000 kg load. Each etched specimen was first examined at X1000 under a microscope having a graduated line segment aligned with the image. This procedure enabled the pearlite line spacing to be measured. All the etched specimens were photographed at X100 to provide the optical microstructure.
4. Results and Discussion
In consultation, with the cutting stand operators, it was determined that a safe handling temperature of the channel at this stage would be about 250˚F (~120˚C) or less, at about 3 - 4 minutes after entry into the cooling bed, as opposed to the prevailing temperature (after forced draft and air cooling) of about 518˚F (270˚C) (this temperature was obtained by actual measurement at the cutting stand of the steel plant using an optical pyrometer). Comparison of the experimental temperature variation with time with FEM temperature variation with time showed reasonably good agreement, justifying the use of FEM values for analysis. FEM results obtained as per details given in Section 2 indicated that using a water spray rate of 5 gpm (18.925 l/m) would result in a channel (mid-flat face) temperature of 245˚F (~118˚C) in 3 minutes. The hardness of the metallographic sample water sprayed at this rate was 165 BHN, which is well within the specification limits of ASTM A-36 channel. However the microstructure as represented in Figure 2(a) showed segregated, rather than uniformly distributed pearlite zones, with a pearlite spacing of 8.69 × 10−4 mm. The pearlite volume fraction was 38%, as compared to the equilibrium fraction of 25% as estimated from the iron-carbon equilibrium diagram. It was therefore decided by the authors to reduce the water spray rate to 4.6 gpm (17.41 l/m) and perform ABAQUS analysis again. It was found that the temperature of the channel at the end of 3 minutes was 291˚F (~144˚C), but when the spray time was extended to 4 minutes the temperature reached was 164˚F (~73˚C), which is very safe for handling purposes. The experimental sample sprayed at 4.6 gpm (17.41 l/m) for 4 minutes showed a hardness of 161 BHN, pearlite spacing of 9.71 × 10−4 mm. and pearlite volume fraction of 30%. As shown by the representative photomicrograph [Figure 2(b)]. The pearlite is more uniformly distributed than in Figure 2(a). It was therefore decided by the authors to adopt this spray rate in their design. As each spray nozzle would cover 4 feet (1.22 m) the design of the water cooling system would incorporate 10 nozzles per channel of length 40 feet (12.2 m) on the cooling bed, in the longitudinal direction. On the same basis, for channels stacked so that the final cooling bed has 24 channels placed side by side, the number of nozzles in the lateral direction would be 4. Thus there would be an array of 40 nozzles placed under the cooling bed. In Figure 3 is shown a schematic diagram of a water spray jet [7].
In order to explain the variation in pearlite spacing and microstructure between the channels sprayed at 5 gpm (18.925 l/m) and 4.6 gpm (17.41 l/m) the FEM-generated cooling curves at the midpoint of the flat face of both (Figure 4) were examined with reference to the continuous cooling transformation (CCT) diagram of a hypoeutectoid 1020 steel, as shown in Figure 5. The coarsening of pearlite spacing in the channel sprayed at 4.6 gpm (17.41 l/m) with respect to the one sprayed at 5 gpm (18.925 l/m) can be readily understood by superimposing the curves of Figure 4 on Figure 5, where the FEM generated cooling curve at 4.6 gpm water spray rate is shown superimposed on the CCT curve. The 5 gpm cooling curve (not shown in Figure 5) cuts the start of proeutectoid, start of pearlite and end of eutectoid transformation curves at lower times compared to the 4.6 gpm cooling curve, As a result the 5 gpm sprayed sample shows finer pearlite spacing but higher volume fraction of pearlite, the pearlite being nonuniformly distributed. On the other hand the cooling curve for the sample sprayed at 4.6 gpm cuts the CCT curvesin Figure 5 at greater times resulting in somewhat coarser pearlite spacing, but with lower
 (a)
(a) (b)
(b)
Figure 2. (a) Optical Microscope Picture ofChannel Water Sprayed; (b) Optical Microscope Picture of Channel Water Sprayed at 4.6 gpm at 5 gpm (18.925 l/m) X100. (17.41 l/m) X100. Dark areas are pearlite Dark areas are pearlite, light areas are ferrite light areas are ferrite.
Figure 3. Schematic diagram of a water spray equipment [7] (this is placed 36 inches under the flat face of channel on the final cooling bed).
volume fraction and better uniformity in pearlite distribution. The theoretical explanation for the variation of microstructure with cooling rate has been provided by Shewmon [8] with validating photomicrographs. The photomicrographs shown by Shewmon indicate that at very slow cooling rates, almost equilibrium conditions are attained resulting in coarse proeutectoid ferrite and coarse pearlite. As the cooling rate is progressively increased, ferrite and pearlite become finer but the volume
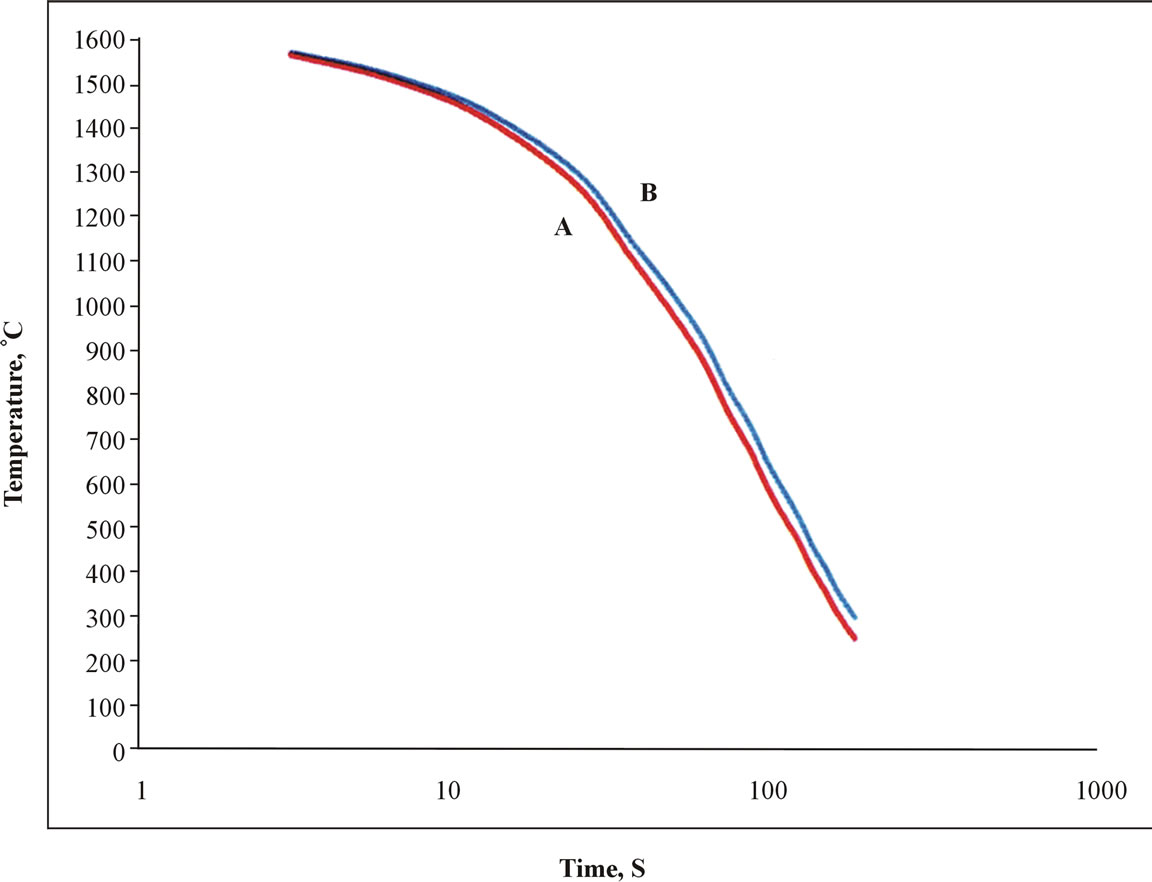
Figure 4. Cooling curves of channel at 5 gpm water spray rate (A) and 4.6 gpm spray rate (B).
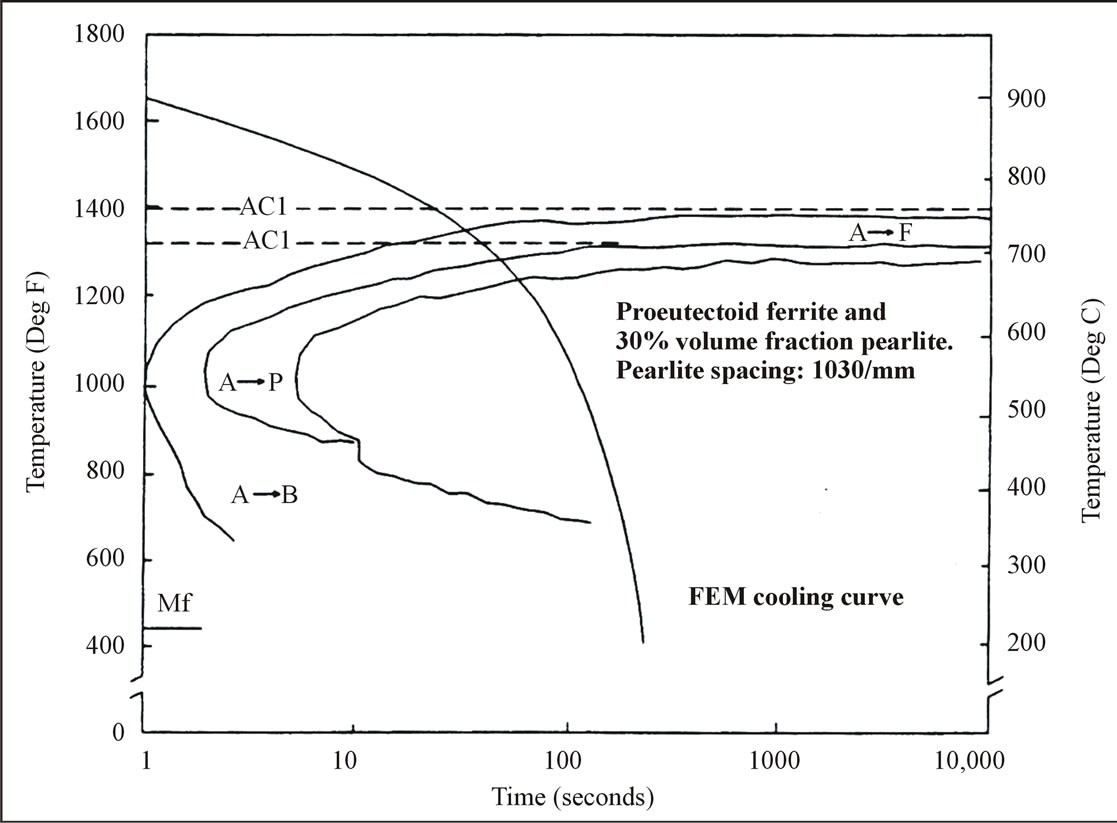
Figure 5. FEM Cooling Curve for 4.6 gpm water spray superimposed on continuous cooling transformation diagram for 1020 steel.
fraction of pearlite increases with respect to the equilibrium proportion. The reason for this trend is the temperature and time dependence of both nucleation rate and growth rate. As the cooling rate is increased, the transformation start and end curves for ferrite and pearlite are cut by the cooling curves at lower temperatures, but the diffusion time is reduced. In the present work the net effect was that as the water spray rate was increased from 4.6 gpm (17.41 l/m) to 5 gpm (18.925 l/m) the pearlite volume fraction increased from 30% to 38% but the pearlite became finer. It should be mentioned in this context that the microstructures shown and discussed refer to only one location in the channel, as noted earlier. The channel corners are subjected to faster cooling and the corresponding microstructure will be different than those shown in this paper; no adverse phase such as martensite was found at any location, including corners. Comprehensive study of the microstructure-cooling rate relationship in the channel, planned in future, would provide good understanding of the effect of the water spray rate of 4.6 gpm on the microstructure and properties of the entire channel. However, for a given location in the channel the arguments presented explain the relative variation in the microstructure. Water spray effects at a much higher rate (6.7 gpm - 25.36 l/m) were also examined in the present work but the results have not been presented in this paper as the hardness obtained was too high for structural applications [1]. The microstructure obtained in this case showed a pearlite volume fraction of 80% and pearlite spacing of 6.54 × 10−4 mm, consistent with the trend shown by Shewmon [8].
5. Summary
An analytical model was developed and solved using FEM to determine the temperature variation with time in an ASTM A-36 channel on the final cooling bed of a mini-steel plant with a view to reduce the temperature of the channel from the existing level to a comfortable level for handling at the cutting stand. The cooling was amplified by using water spray at the bottom of the channel. The effect of water spray rate on the microstructure and hardness at a given location in the channel was studied experimentally using a specially fabricated water spray unit to simulate the analytical model. The results indicate that a water spray rate of 4.6 gpm (17.41 l/m) for 4 minutes gives a very comfortable temperature for handling, accompanied by a good microstructure and hardness. For a channel of length 40 feet (~12.2 m), ten equally spaced water spray nozzles are required, assuming that each nozzle covers a span of 4 feet (1.22 m) in the horizontal direction. Assuming that the final cooling bed has 24 channels placed side-by-side, 4 nozzles would be needed in the lateral direction. Thus an array of 40 nozzles, 10 per row, placed about 3 feet below the cooling bed would be needed to bring down the temperature of the array of channels to a comfortable temperature for handling at the cutting stand, consistent with a good microstructure and hardness in the channels.
Acknowledgements
The authors are grateful to the management of Nucor Steel Corporation, Jewett, Texas for allowing them to visit the plant and inspect the final cooling bed. The channel sample provided by them for metallographic examination is also gratefully acknowledged.
REFERENCES
- S. Rachamadagu, “Controlled Heat Trasfer of Hot Rolled Products on the Cooling Bed,” M.S. Thesis, Texas A&M University, College Station, 1993.
- R. J. Golstein, E. M. Sparrow and D. C. Jones, “Transfert Massique par Convection Naturelle Adjacente a des Plaques Horizontales,” International Journal of Heat and Mass Transfer, Vol. 16, 1973, p. 1025.
- J. R. Lloyd and W. R. Moran, “Natural Convection Adjacent to Horizontal Surfaces of Various Platforms,” ASME Paper 74-WA/HT-66, 1974.
- J. E. Hilliard and J. W. Cahn, “An Evaluation of Procedures in Quantitative Metallography for Volume Fraction Analysis,” Transactions AIME, Vol. 221, 1961, pp. 344- 352.
- E. Schmidt and W. Beckmann, “Das Temperatur und Geschwindigkeitsfeld von Einer Warmeabgebenden Senkreschten platte bei Natralischer Konvektion,” Tech, Mech, Thermodynamick, Vol. 1, 1930, p. 341.
- M. Bamberger and B. Prinz, “Determination of Heat Transfer Coefficients during Water Cooling of Metals,” Materials Science and Technology, Vol. 2, No. 4, 1986, pp. 410-415. http://dx.doi.org/10.1179/mst.1986.2.4.410
- http://www.dultmeier.com/products/0.811.816/3125
- P. G. Shewmon, “Transformations in Metals,” McGrawHill Book Company, New York, 1969, p. 248.
Nomenclature (The Units as Applicable Are Shown in Each Equation or Expression)
T = temperature t = time
Δt = time step
α = thermal diffusivity = k/cρ
k= thermal conductivity c = specific heat
ρ = density x = horizontal distance y = vertical distance Nu = Nusselt number Re = Rayleigh number Gr = Grashoff number
Pr = Prandtl number
µ = absolute viscosity
ν = kinematic viscosity
λ = heat transfer coefficient of water spray
λν = heat transfer coefficient at film boiling stage
λrad = radiative heat transfer coefficient
θs = surface temperature of steel
θb = temperature of cooling water
θc = evaporation temperature of cooling water

