Modern Mechanical Engineering
Vol.3 No.2(2013), Article ID:31643,5 pages DOI:10.4236/mme.2013.32012
Study of Diffusion Instability in Some Ternary Gas Mixtures at Various Temperatures
1Institute of Experimental and Theoretical Physics, Al-Farabi Kazakh National University, Almaty, Kazakhstan
2Atyrau Institute of Oil and Gas, Atyrau, Kazakhstan
3National Research University Moscow Energy Institute, Moscow, Russia
Email: fedor23.04@mail.ru
Copyright © 2013 Vladimir Kossov et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received December 24, 2012; revised March 26, 2013; accepted April 17, 2013
Keywords: Diffusion; Convection; Diffusion Instability; Linear Theory of Stability; Rayleigh Numbers
ABSTRACT
Within the linear theory of stability, the process of isothermal mixing of three-component gas mixtures in a channel of final dimensions in the absence of mass-transfer through its walls is considered. The comparison of experimental data with the results of theoretical calculations for the mixtures He+Ar-N2 and H2+N2-CH4 is shown, that a stable diffusion process as the temperature increased will remain the same and be described by the ordinary diffusion laws, but unstable one lost its intensity and tend to the stable diffusion.
1. Introduction
The study of a diffusion process in multicomponent gas mixtures showed that mutual influence of components to each other under certain conditions lead to phenomena no taking place in ordinary binary diffusion. One of the most interesting peculiarities both in scientific and practical application is diffusion instability [1]. Diffusion instability is characterized by strong convective flows, which considerably exceed purely molecular transfer substantially distorting presumable results. Previous experiments showed that the process of diffusion instability depends on certain conditions and parameters, for example, pressure, concentration, temperature, viscosity, geometry of diffusion channel and etc. [2-6].
The determination of a transition boundary of mixture from the stable state to the unstable one and back is one of the main factors in the study of regime change of mixing. In the paper [1], the stability limits for the onset of convection in ternary gaseous mixture having a density inversion are obtained with a stability theory based on Rayleigh’s treatment and the Stefan-Maxwell equations [7]. However, the theory outlined in this paper is only approximate, and the agreement with experiment is far from perfect.
Experimental data reported in [2-6] in their physical meaning resemble the problem of instability which arises under conditions of thermal convection [8-10]. Application of stability theory [11] allowed formulating an approach to revealing common regularities in determining the transition from the diffusion regime to the gravitational concentration convection. This methodology was used to determine the stability limits of isothermal threecomponent gas mixtures in the case of a horizontal plane layer or in the form of an infinite plane vertical slot [12]. However, the geometry of the considered problem made it possible to achieve just qualitative agreement with the experiment as a cylindrical channel was used in [2-6]. Solving the stability problem of ternary gas mixtures in conditions maximally approximate to the experiment becomes a question of fundamental importance.
The aim of this study is to examine the transition from the state of diffusion to the regime of concentration gravitational convection (diffusion instability) in a channel of finite size in the absence of mass-transfer through its wall. In addition, the obtained data are compared with the experiments presented in [2], where the transition from the state of diffusion to the regime of convection is studied at different temperatures.
2. Mathematical Model of Diffusion Instability
2.1. General System of Equations
The macroscopic flow of the isothermal ternary gas mixture is described by the general system of the hydrodynamic equations, that includes the Navier-Stokes equations, equations for conservation of the number of particles in the mixture and the components. Taking into account the conditions of independent diffusion, for which the 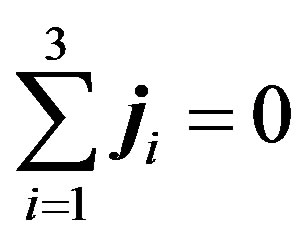 and
and 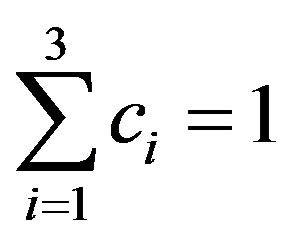 are valid, the system of equations takes the following form [11]:
are valid, the system of equations takes the following form [11]:
 (1)
(1)
where “practical” coefficients of three-component diffusion are defined in accordance with expressions:

where  are the mutual diffusion coefficients indicating interference of two components.
are the mutual diffusion coefficients indicating interference of two components.
The system of Equation (1) is supplemented with the environmental state equation

interrelating the thermodynamic parameters entering into the system of Equation (1).
The method of small perturbations [11] has been used by solution of the system of Equation (1). Taking into account that at L » r (L, r are the length and radius of diffusion channel accordingly) the differences between perturbations of the average 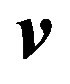 and weight-average
and weight-average  velocities in the Navier-Stokes equation will be inconsiderable, then the final system of equations of gravitational concentration convection for perturbation values in dimensionless quantities takes the form:
velocities in the Navier-Stokes equation will be inconsiderable, then the final system of equations of gravitational concentration convection for perturbation values in dimensionless quantities takes the form:
 (2)
(2)
where 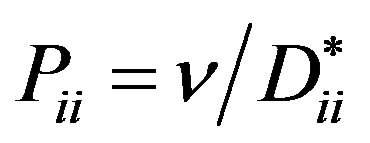 is the Prandtl diffusion number,
is the Prandtl diffusion number,  is the Rayleigh partial number,
is the Rayleigh partial number, 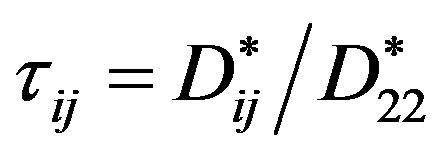 denotes the parameters, which determine the relationship between the “practical” diffusion coefficients.
denotes the parameters, which determine the relationship between the “practical” diffusion coefficients.
2.2. Line of Stability for a Limited Cylindrical Diffusive Channel
Three-dimensional motions are essential in the diffusion cylindrical channel of final length. Therefore, when approximating the velocity, it is necessary to consider all components of the vector  differ from zero. Examining the periodical motions along φ in the cylindrical coordinate and satisfying the conditions on the hard boundaries
differ from zero. Examining the periodical motions along φ in the cylindrical coordinate and satisfying the conditions on the hard boundaries 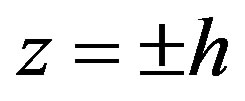 (
(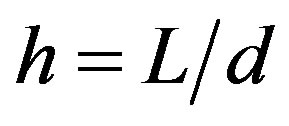 is the geometry parameter characterizing stability), the velocity approximation can be written as [11]:
is the geometry parameter characterizing stability), the velocity approximation can be written as [11]:
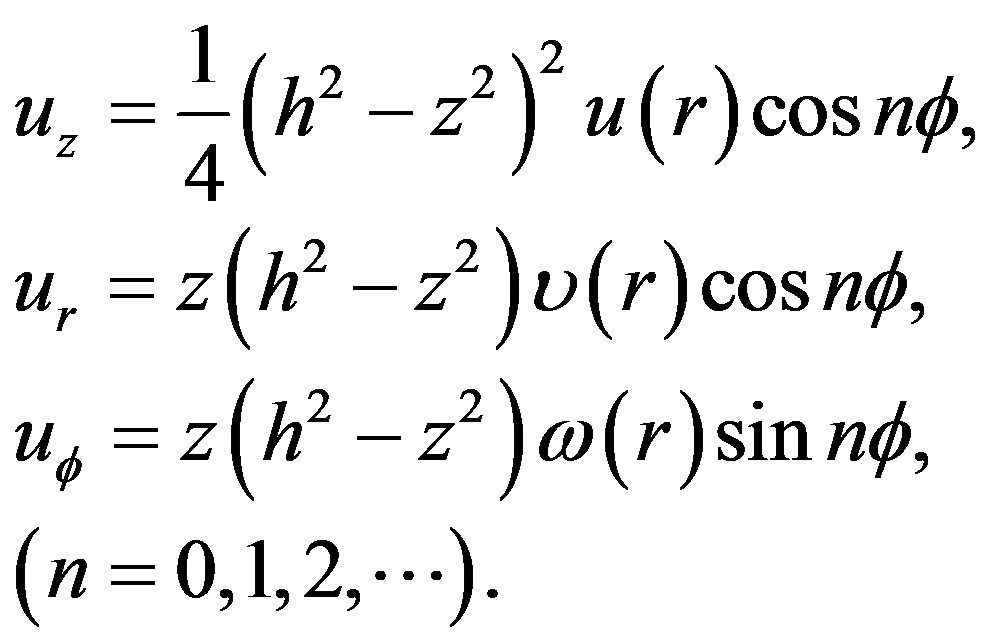 (3)
(3)
The radial functions u, υ, ω should be vanish on the hard lateral surface of cylinder (at ). The relation binding these functions follows from the continuity equation:
). The relation binding these functions follows from the continuity equation:

though
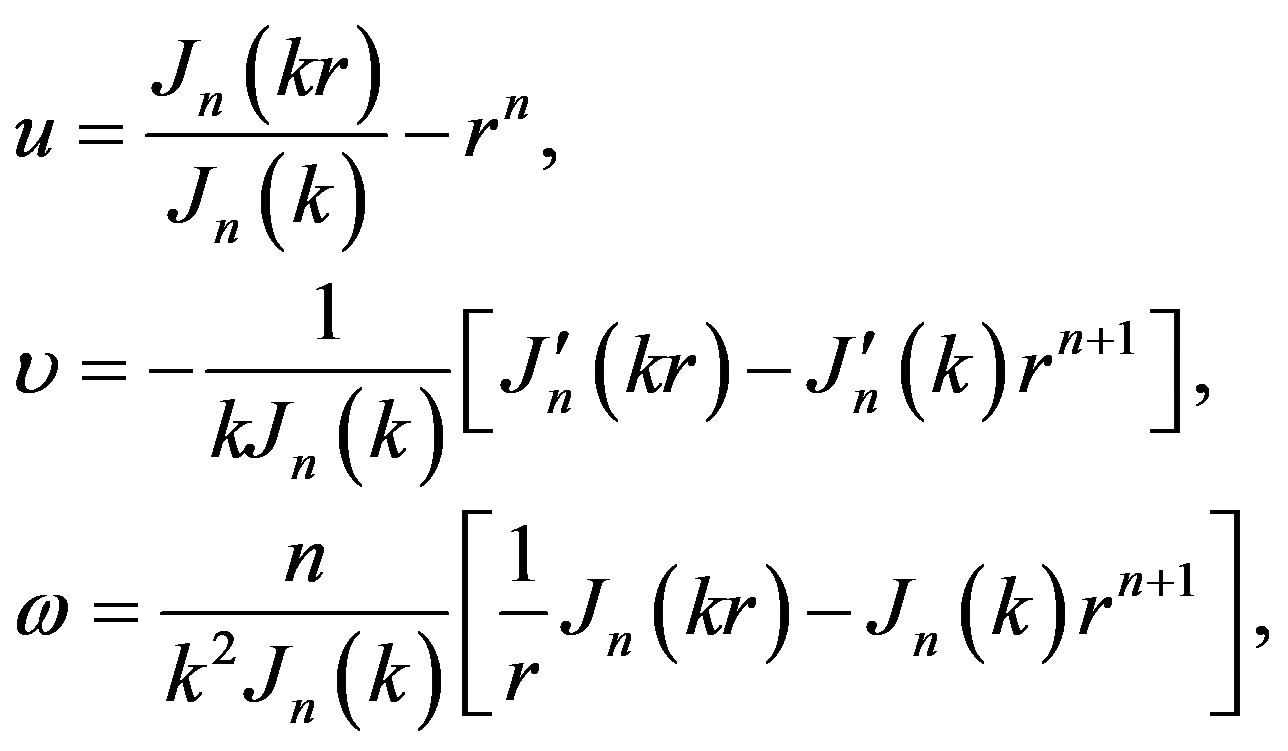 (4)
(4)
where 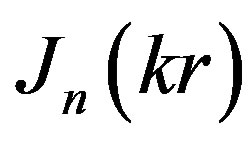 is n-order Bessel function, but the parameter k can be found from the equation:
is n-order Bessel function, but the parameter k can be found from the equation:
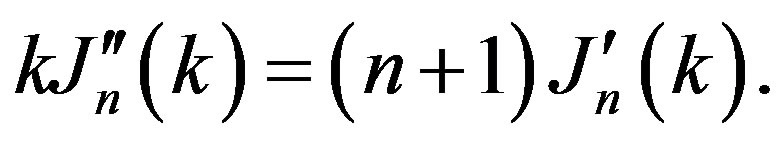 (5)
(5)
Assuming for the first two equations in the set of Equations (2), that , we determine the concentration of components from the following equations:
, we determine the concentration of components from the following equations:

where 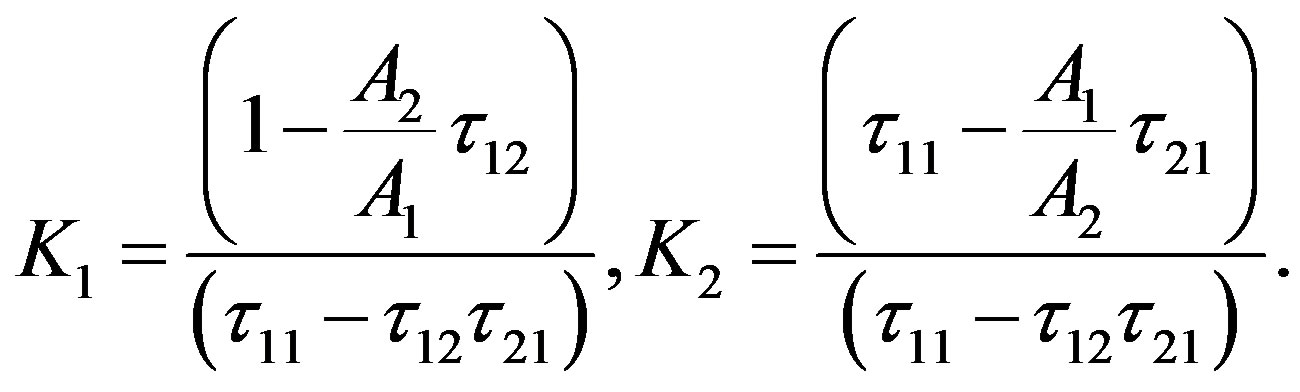
We will consider, that , then
, then
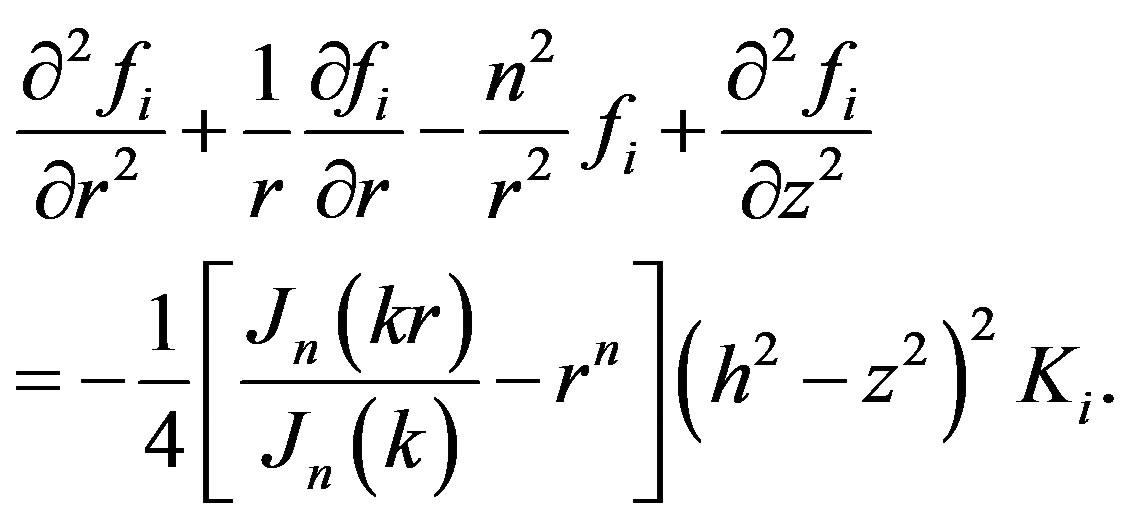 (6)
(6)
Supposing that the perturbations of concentrations vanish  on the end surface
on the end surface , then the additional condition implying that the second derivative vanishes at the ends of diffusion channel results from Equation (6):
, then the additional condition implying that the second derivative vanishes at the ends of diffusion channel results from Equation (6):
 (7)
(7)
that permits to select the following approximation:
 (8)
(8)
where is the radial function of concentration.
is the radial function of concentration.
For determination 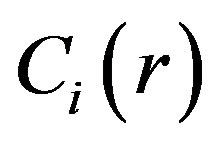 we use Kantorovich method. Substituting Equation (8) into Equation (6), multiplying by depending on z part of the function
we use Kantorovich method. Substituting Equation (8) into Equation (6), multiplying by depending on z part of the function 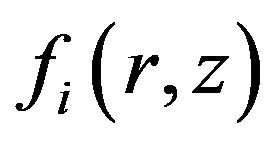 and integrating between – h and h we obtain the equation:
and integrating between – h and h we obtain the equation:
 (9)
(9)
where  Finding components concentrations of Equation (9) were solved with the boundary condition
Finding components concentrations of Equation (9) were solved with the boundary condition , and then the final solution in the center becomes (see Equation (10)):
, and then the final solution in the center becomes (see Equation (10)):
where Jn and In are n-order Bessel functions of the first kind.
In order to determine the monotonous stability boundary of the problem under consideration, the third equation of the system (2) can be scalarly multiplied by the vector  and integrated all over the volume V of the diffusion channel. This can be done under the conditionsthat
and integrated all over the volume V of the diffusion channel. This can be done under the conditionsthat . Then we have:
. Then we have:
 (11)
(11)
This equation in the coordinates 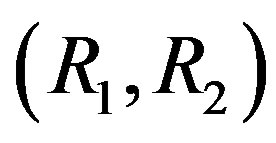 gives a straight line MM, dividing the region of molecular transport and the region of the diffusion instability. Figures 1 and 2 show the location of the neutral line of monotonic instability for the systems He+Ar-N2 and H2+N2-CH4 for
gives a straight line MM, dividing the region of molecular transport and the region of the diffusion instability. Figures 1 and 2 show the location of the neutral line of monotonic instability for the systems He+Ar-N2 and H2+N2-CH4 for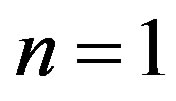 . The region that lies below the line MM corresponds to diffusion.
. The region that lies below the line MM corresponds to diffusion.
From the condition of zero density gradient of the mixture and with allowance for the determined values of partial Rayleigh numbers (2), we obtain the following equation for the line in the plane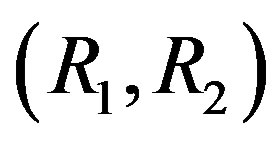 :
:
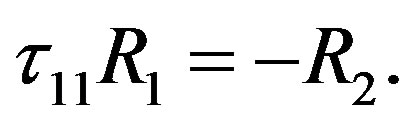 (12)
(12)
The mutual position of the line of monotonic instability MM (Equation (11)) and the line  (Equation (12)) for
(Equation (12)) for  is shown in Figures 1 and 2. As follows from figures, there exists a region in the plane
is shown in Figures 1 and 2. As follows from figures, there exists a region in the plane  where the line MM is situated below the line (12). In this region, the mixture appears to be unstable.
where the line MM is situated below the line (12). In this region, the mixture appears to be unstable.
3. Results of Numerical Experiment
To compare the approach proposed in Paragraph 2 with the experimental data is shown in [2] we represent them in the form of partial Rayleigh numbers. The partial Rayleigh numbers in accordance with (2) can be written as follows:
 (13)
(13)
where 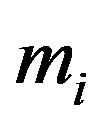 is the molecular mass of the i-th component,
is the molecular mass of the i-th component,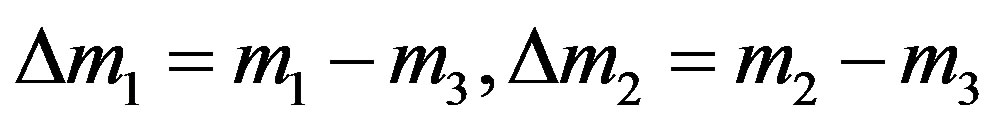 . If conditions of the experiment are known (pressure, temperature, composition of mixtures in each of the flasks, the size of the diffusion channel), then according to Equation (13) we can find R1 and R2 and thus determine the point representing this experiment on the plane
. If conditions of the experiment are known (pressure, temperature, composition of mixtures in each of the flasks, the size of the diffusion channel), then according to Equation (13) we can find R1 and R2 and thus determine the point representing this experiment on the plane . From experiment, we know what the regime (diffusion or convection) occurs under the given conditions. In addition, we assume that the number 1 refers to the component with the lowest density, while the numbers 2 and 3 refer to the components with the highest and intermediate densities respecttively.
. From experiment, we know what the regime (diffusion or convection) occurs under the given conditions. In addition, we assume that the number 1 refers to the component with the lowest density, while the numbers 2 and 3 refer to the components with the highest and intermediate densities respecttively.
Figures 1 and 2 show the experimental data in terms of the Rayleigh numbers for the systems 0.4688Не(1)+0.5312Ar(2)-N2(3) and 0.6179Н2(1)+0.3821N2(2)-CH4(3) and for the systems 0.6192Не(1)+0.3808Ar(2)-N2(3) and 0.6463Н2(1)+0.3537N2(2)-CH4(3) respectively, obtained by varying the temperature. The full circles correspond to the convective mixing process while the open circles conform to the diffusion one.
|
|
 (a)
(a) (b)
(b)
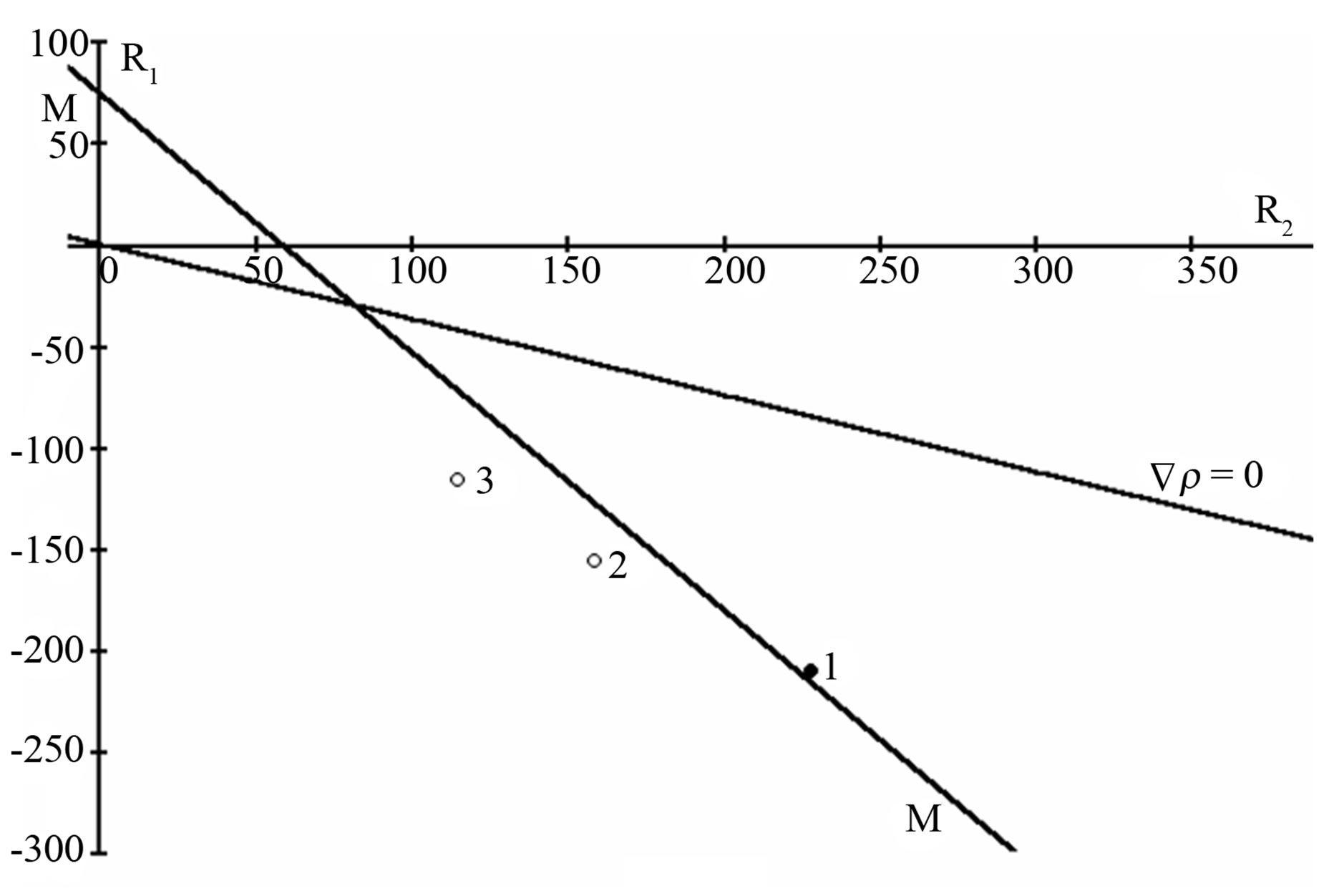
Figure 1. (a) Boundary lines of monotonic instability MM and zero density gradient  for the system 0.4688Не +0.5312Ar-N2. Symbols ● correspond to data that determine unstable state. The calculation is carried out at the temperatures values: T = 293.0 (1), 313.0 (2), 333.0 (3), 353.0 (4) K. (b) Boundary lines of monotonic instability MM and zero density gradient
for the system 0.4688Не +0.5312Ar-N2. Symbols ● correspond to data that determine unstable state. The calculation is carried out at the temperatures values: T = 293.0 (1), 313.0 (2), 333.0 (3), 353.0 (4) K. (b) Boundary lines of monotonic instability MM and zero density gradient 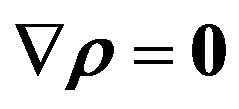 for the system 0.6179Н2+ 0.3821N2-CH4. Symbols ● correspond to data that determine unstable state. The calculation is carried out at the temperatures values: T = 273.0 (1), 293.0 (2), 313.0 (3), 333.0 (4), 353.0 (5) K.
for the system 0.6179Н2+ 0.3821N2-CH4. Symbols ● correspond to data that determine unstable state. The calculation is carried out at the temperatures values: T = 273.0 (1), 293.0 (2), 313.0 (3), 333.0 (4), 353.0 (5) K.
On Figures 1, all points displaying the experiment are situated in the area of instability (region between the line stability MM and the line of zero density gradient), but with temperature rise tend to the region of stable diffusion (region below the line MM).
As is seen, in Figure 2(a) that at the temperature 353.0 K the system 0.6192Не+0.3808Ar-N2 is in the area of stable diffusion. It is conformed to the data given in [2]. According to Figure 2(a) point 1 corresponds to the temperature 293.0 K is situated practically at the curve of monotonic disturbances. That indicates the instable process observes at the considered temperature. Figure 2(b) shows that for the system 0.6463Н2+0.3537N2-CH4 transition into the unsteady regime occurs at the temperature 323.0 K.
Thus, the results reveal that the unstable diffusion process tends to stable one by raising the temperature, but a decrease in the temperature can cause transition to the unstable state of a diffusion-stable system.
4. Conclusion
In this paper, we have studied the instability of mechanical equilibrium (diffusion instability) in ternary gas mixtures at different temperatures. Linear stability theory is applied to determine the boundary of transition from the state of diffusion to the region of the concentration convection. The problem has been solved for a cylindrical channel of finite size and boundary conditions, suggesting the absence of component transfer through the walls of the diffusion channel. The comparison of theoretical results with the experimental data for the study of the
 (a)
(a) (b)
(b)
Figure 2. (a) Boundary lines of monotonic instability MM and zero density gradient  for the system 0.6192Не +0.3808Ar-N2. Symbols ○, ● correspond to data that determine stable and unstable state respectively. The calculation is carried out at the temperatures values: T = 293.0 (1), 323.0 (2), 353.0 (3) K. (b) Boundary lines of monotonic instability MM and zero density gradient
for the system 0.6192Не +0.3808Ar-N2. Symbols ○, ● correspond to data that determine stable and unstable state respectively. The calculation is carried out at the temperatures values: T = 293.0 (1), 323.0 (2), 353.0 (3) K. (b) Boundary lines of monotonic instability MM and zero density gradient  for the system 0.6463Н2+0.3537N2-CH4. Symbols ○, ● correspond to data that determine stable and unstable state respectively. The calculation is carried out at the temperatures values: T = 293.0 (1), 323.0 (2), 353.0 (3) K.
for the system 0.6463Н2+0.3537N2-CH4. Symbols ○, ● correspond to data that determine stable and unstable state respectively. The calculation is carried out at the temperatures values: T = 293.0 (1), 323.0 (2), 353.0 (3) K.
temperature dependence of the diffusion mixing of ternary gas mixtures He+Ar-N2 and H2+N2-CH4 indicates qualitative and quantitative agreement. Therefore, it can be concluded that the proposed calculation technique permits estimation of the critical parameters of the transition to the unstable regime.
5. Acknowledgements
This work has been performed under the support of the Fund of Science of the Ministry of Education and Science of Republic of Kazakhstan (the project number: No. 1134/GF).
REFERENCES
- L. Miller and E. A. Mason, “Oscillating Instabilities in Multicomponent Diffusion,” Physics of Fluids, Vol. 9, No. 4, 1966, pp. 711-721. doi:10.1063/1.1761737
- Yu. I. Zhavrin and V. N. Kosov, “Effect of Temperature on Diffusional Instability,” Journal of Engineering Physics, Vol. 55, No. 1, 1988, pp. 774-778. doi:10.1007/BF00878123
- Yu. I. Zhavrin, A. Z. Aitkozhaev, V. N. Kosov and S. A. Krasikov, “Effect of Viscosity on Stability of Diffusion Mass Transfer in Isothermal Three-Species Gas Systems,” Technical Physics Letters, Vol. 21, No. 3, 1995, pp. 206- 207.
- Yu. I. Zhavrin, N. D. Kosov, S. M. Belov and S. B. Tarasov, “Effect of Pressure on the Diffusion Stability in Some Three-Component Gas Mixtures,” Zhurnal Tekhnicheskoi Fiziziki, Vol. 54, No. 5, 1984, pp. 943-947.
- Yu. I. Zhavrin, V. N. Kosov, D. U. Kul’zhanov, I. V. Poyarkov and N. B. Ankusheva, “Effect of Cell Rotation Speed on Mutual Diffusion in a Three-Component Gas Mixture,” Technical Physics Letters, Vol. 29, No. 2, 2003, pp. 108-110. doi:10.1134/1.1558740
- V. N. Kossov, N. B. Ankusheva and V. D. Seleznev, “Effect of Diffusion Channel Inclination on Stability of Mechanical Equilibrium in Isothermal Binary Gas Mixtures,” Journal of Applied Mechanics and Technical Physics, Vol. 51, No. 1, 2010, pp. 62-64. doi:10.1007/s10808-010-0009-y
- J. O. Hirschfelder, Ch. F. Curtiss and R. Bird, “Molecular Theory of Gases and Liquids,” John Willey & Sons, Inc., New York, 1954.
- D. D. Joseph, “Stability of Fluid Motions,” Springer, Berlin, 1976.
- L. Kh. Ingel, “Convective Instability Mechanism for a Binary Mixture at a Vertical Surface,” Technical Physics, Vol. 54, No. 2, 2009, pp. 204-209. doi:10.1134/S1063784209020078
- S. Chen, J. Tӧlke and M. Krafczyk, “Numerical Investigation of Double-Diffusive (Natural) Convection in Vertical Annuluses with Opposing Temperature and Concentration Gradients,” International Journal of Heat and Fluids Flows, Vol. 31, No. 2, 2010, pp. 217-226. doi:10.1016/j.ijheatfluidflow.2009.12.013
- G. Z. Gershuni and E. M. Zhukhovitskii, “Convective Stability of Incompressible Fluids,” Keter, Jerusalem, 1976.
- V. N. Kosov, V. D. Seleznev and Yu. I. Zhavrin, “The Diffusion Instability of Isothermal Three-Component Gas Mixtures,” Thermophysics and Aeromechanics, Vol. 7, No. 1, 2000, pp. 127-135.


