Modern Mechanical Engineering
Vol.2 No.3(2012), Article ID:22195,6 pages DOI:10.4236/mme.2012.23011
Investigation of Stresses on Tie Band Used to Wrap and Fasten Rolled Coils
1College of Mechanical and Control Engineering, Handong Global University, Pohang, Korea
2School of Mechanical Engineering, Yeungnam University, Gyeongsan, Korea
Email: *cslee@handong.edu, ilchung@yu.ac.kr
Received May 18, 2012; revised June 25, 2012; accepted July 4, 2012
Keywords: Tie Band; Rolled Coil; Springback Stress; Elastic Recovery; Strain Gauge
ABSTRACT
The research was motivated to establish a scientific basis for the required number of steel tie bands used in wrapping and fastening hot rolled coils produced in steel manufacture lines for safe delivery and storage. Strain gages were installed on the tie bands and stress was recorded during the banding and delivery procedure of rolls in the field. The stress developing in the bands due to fastening of the roll and that due to springback of the coil were clearly distinguishable from the strain gage signals. Twelve hot rolled coils having different yield strength, thickness, width, and weight were tested in the recoiling field. The results showed the average tensile stress developing in the bands due to the fastening of the roll to be 151.7 ± 53.8 MPa, which corresponded to one fourth of the failure strength of the steel band in the buckle region. In addition to the stress caused by fastening, average tensile stress caused by springback of the rolled coils was estimated to be 33 MPa. It increased to 79 MPa when one of the tie bands was removed from the roll. Comparing the measured stress due to springback with the theoretical stress formula yielded a proportional constant value of 0.219, and a correlation coefficient of 0.914, which demonstrate the formula to be useful in predicting springback stress. The average safety factor of the tie band was found to be 3.26 and it decreased to 2.60 when one of the bands was removed from the roll. The safety factor of the band was found to decrease with increased coil thickness because the current factory standard on the number of bands does not significantly take into account of increase in the springback force with increased coil thickness.
1. Introduction
Steel manufacture companies have their own standards on the number of steel tie bands used to wrap and fasten hot rolled coils. As shown in Figure 1, the longitudinal bands (L-band) are mainly used to protect a roll from uncoiling and the circumferential bands (C-bands) are used in preventing coil layers from slipping to the sides.

Figure 1. Rolled coils fastened by longitudinal bands (LBand) and circumferential bands (C-Band) for safe delivery and storage. Buckles are used to tightly fasten the bands.
In general, the factory standard for the number of tie bands considers coil thickness and weight of the roll. However, these standards have been established with little scientific bases. Therefore, different numbers of tie bands are used depending on the work field even when the coils are similar in thickness and weight. The difference in the number of tie bands was reported to be as many as two times according to the workers in the field. If reasonable engineering bases are to be established on the required number of tie bands for safe delivery and storage of the rolls, one would expect to eliminate unnecessary bands and reduce cost and man hour for the banding work.
The main function of tie bands is to prevent uncoiling of the rolled coil caused by its tendency of elastic recovery. This phenomenon is called springback [1]. Another function is to protect the roll from possible impact during delivery and storage. The bands are wrapped around the roll and each one is tightly fastened by a buckle using air-pressured guns.
This research was conducted to estimate the stress on the tie bands caused by the fastening force of the band buckle and the spring-back force of the coil, and hence to establish a scientific basis for the proper number of tie bands for rolls. Stress measurements were conducted on the tie bands for various coil dimensions and material strengths. The unknown proportional constant of the springback formula was determined by comparing a theoretical formula for spring-back stress with the experimental results. The results were applied to evaluate safety factors on the standard number of the tie bands used by the local company, POSCO (Pohang Iron & Steel Company Ltd.).
The target material of the current research was hotrolled steel rolls with coil thickness between 1.5 mm and 20 mm, roll width between 730 mm and 1860 mm, yield strength between 200 MPa and 600 MPa, roll weight between 8 ton and 35 ton, and inner coil radius of 760 mm. The tie bands used in the experiment had cross sections of 0.9 mm by 32 mm, ultimate tensile strength of 950 MPa, stretching limit of 10%, and Vickers hardness of 260. The experiments were performed in the recoiling field of the local company for six months.
2. Theory
2.1. Stress in Tie Band
The stress developing in the tie bands is attributed to the following three mechanisms.
Ÿ Stress caused by curvature (outer radius) of the roll.
Ÿ Stress caused by fastening force of the band buckle.
Ÿ Stress caused by springback of the coil.
The stress caused by the curvature of the roll is simply calculated from the bending formula [2] since the band deforms following the roll radius. Stress is expressed as Equation (1) where E presents elastic modulus of the band material, R is outer radius of roll (same as the radius of curved band), and tb is band thickness.
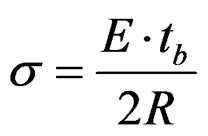 (1)
(1)
Because the elastic modulus of steel does not significantly vary between different coils, the stress caused by curvature is proportional to band thickness and inversely proportional to roll radius.
The stress that develops when bands are fastened onto the roll depends on the magnitude of air pressure in the gun used in fastening the band buckle. Because the air pressure of the gun is maintained to be a constant value, this stress is supposedly controllable. However, our experiment showed that the stress tended to vary significantly between different coils.
The theoretical formula for stress caused by springback of coils was derived as Equation (5) (see next section). The springback stress is proportional to the yield strength of the coil material, the roll width, and the square of the coil thickness, while it is inversely proportional to the number of bands and outer radius of the roll. Therefore, among the three kinds of stress developing in the band, the springback stress showed the largest variation in magnitude depending on coils.
2.2. Stress in Tie Band
As the coils are subjected to a maximum strain within 1% on the recoiling field, a model with a perfectly linear elastic-plastic deformation can be employed without considering strain hardening [3,4]. Furthermore, for the tensile stress caused by the stretching of coils during the recoiling process, which is known to be around 10% of the yield strength, a simple springback Equation is to be used ignoring the stretch effect [3,5].
Therefore, the springback moment of the coil can be calculated from the linear elastic stress distribution along the thickness of the coil as shown in Figure 2 since the elastic portion of stress is attributed for the uncoiling force of the coil. Equation (2) calculates the springback moment by integrating the moment of the force acting on the rectangular cross section of the coil with respect to the neutral axis [2].
 (2)
(2)
In Equation (2), t represents coil thickness, b represents coil width, and σy stands for yield strength.
As shown in Figure 3, the tensile force in the L-band,
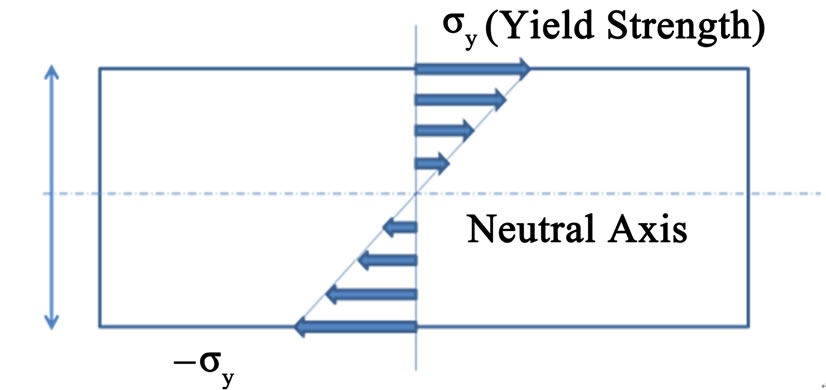
Figure 2. Linear elastic stress distribution in coil with thickness t and yield strength σy.

Figure 3. Tensile force T in the band, pressure P due to springback of coil, and friction force μP developing between the band and the outer layer of the coil. R is radius of the roll.
labeled as T, can be determined by applying the moment equilibrium between the uncoiling moment of the coil and the frictional moment provided by the band. Equation (3) means that the uncoiling moment of the roll by spring-back, Mspringback, is balanced by the moment of the friction force, P, developing between the band and the outer layer of the coil.
In Equation (3), the springback pressure, P, and the friction force, μP, are assumed to develop in only one layer of coil (2πR in circumferential length) and remain constant. The moment arm in the equation equals to the roll radius, R.
 (3)
(3)
By combining Equations (2) and (3), the tensile force in the band can be expresses as in Equation (4).
 (4)
(4)
As we consider the number of bands, N, the stress developing in the band can be expressed as in Equation (5).
 (5)
(5)
The explanations of variables appearing in Equation (5) are as follow. σy: yield strength of coil (MPa); b: coil width (mm); t: coil thickness (mm); R: outer radius of roll (mm); N: number of bands; Ab: cross section area of band (mm2).
Equation (5) was obtained by considering the elastic recovery of one coil layer under a perfectly linear elastic-plastic deformation. However, there are many coil layers in the roll and hence friction forces developing in every layer needs to be considered. The constant in Equation (3), or 2π, considers one coil layer and therefore it is no longer valid for the roll with many coil layers. Consequently, the proportional constant, 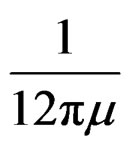 in Equation (5) is also invalid and needs to be determined based on the experimental measurements in this study.
in Equation (5) is also invalid and needs to be determined based on the experimental measurements in this study.
3. Experimental Method
3.1. Stress Measurement
A strain gage measurement system was set up and brought in the recoiling field. It had eight channels and each channel was designed as a quarter bridge with a dummy gage for temperature compensation [6]. Figure 4 shows the schematics of the measurement system. The strain signals were fed to a laptop computer through a NI PCMCIA-6014 data acquisition card. Labview was employed to display and save data at 100 Hz sampling rate. Taking into account the difficulties in accessing the roll, a 15 m long cable was attached to each strain gage.
The C-bands showed lower stress than the L-bands because the C-bands’ main function was to keep the coil from sliding between its layers. Major stress was observed in the L-bands, and therefore strain gages were installed only on L-bands although both L and C-bands were used to fasten the roll.
Figure 5 illustrates the experimental procedure. Before the roll arrived at the station, strain gages were installed on the L-bands. As a roll arrived at the station, the bands were carefully bended and wrapped on the roll. A pneumatic gun was applied to tightly fasten the band buckle. After all the bands were installed, a crane driver was called to come and lifted the roll about 50 cm above the skid on the ground and released it smoothly after 10 seconds. As the roll was lifted, the coil tended to uncoil and the band stress was suddenly raised due to the springback force. As the roll was released on the skid, spring-back was oppressed by the weight of the roll and
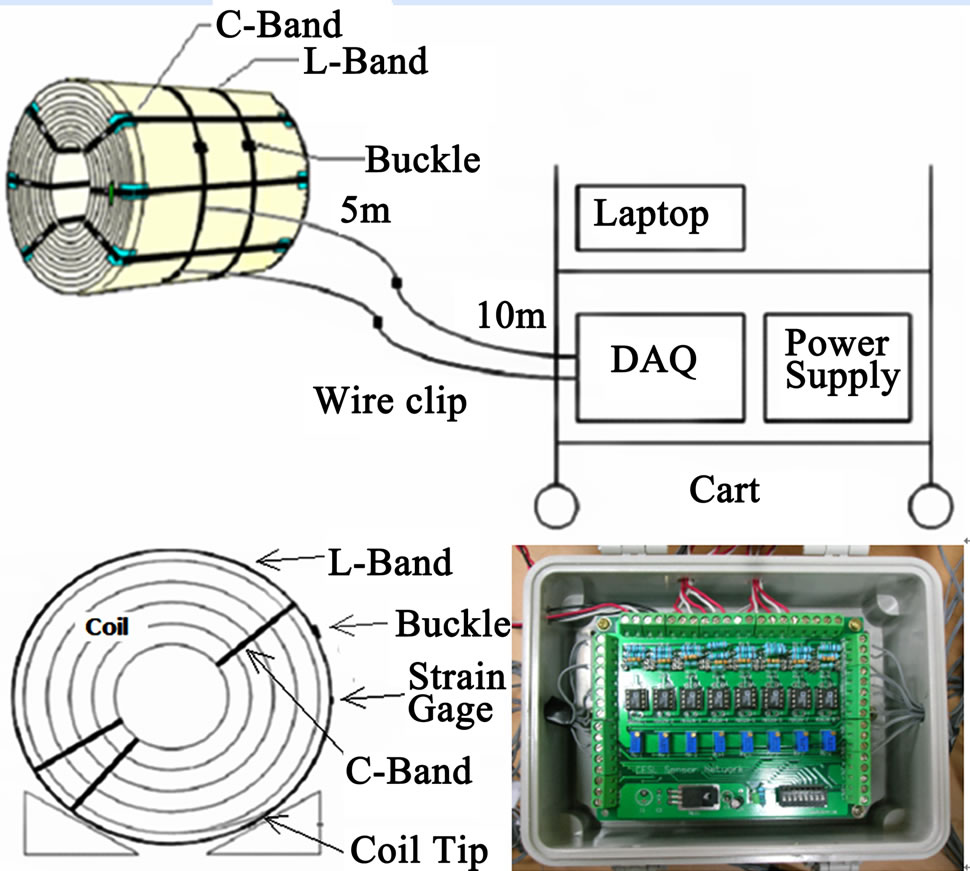
Figure 4. Schematics of stress measurement system.
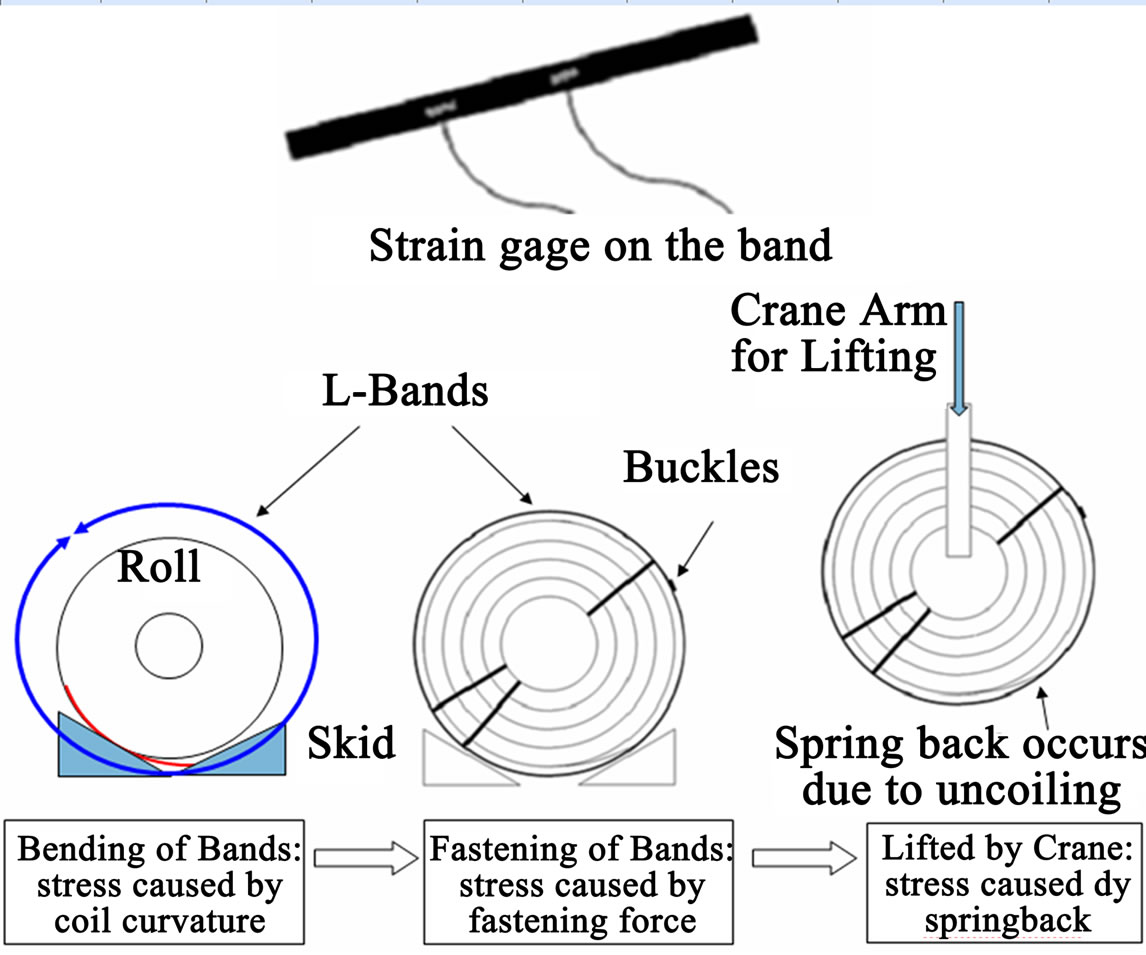
Figure 5. Sequence of stress measurement.
stress reduction occurred in the band. The process of lift and release was repeated to observe subsequent changes in the band stress. In order to observe changes in the stress with less number of bands than the factory’s standard number, the experiment was repeated with one L-band cut from the roll.
3.2. Coils Tested
Dimensions and strength of the coil tested in the study are listed in Table 1. The experiments were conducted for rolls with coil thickness between 2.5 mm and 11.3 mm, roll width between 811 mm and 1212 mm, yield strength between 205 MPa and 449 MPa, and roll weight between 9.7 ton and 23.7 ton.
4. Results and Discussion
4.1. Strength of Tie Band
The strength of the tie band was tested in POSCO technology research center [7]. The tensile strength of the band material alone was estimated to be about 939 MPa. However, when the tie band was tested with the band buckle fastened as shown in Figure 6, the buckle failed in the joining region with the band before the band failed and the average failure strength of the buckle was estimated to be 601 ± 39 MPa. Therefore, the strength of the buckle was used as the ultimate strength of the tie band.
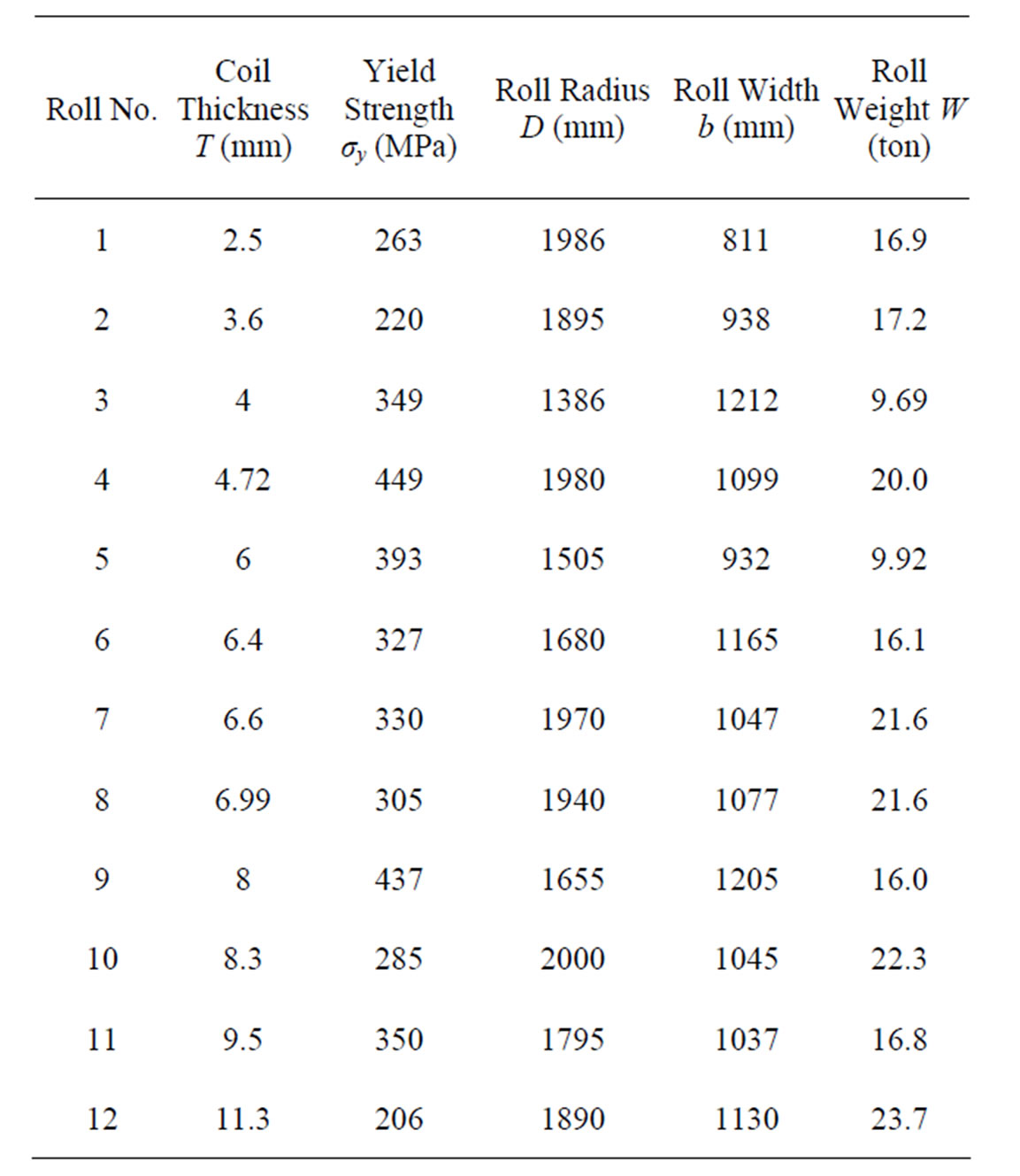
Table 1. Dimensions and strength of coils tested in the study.
4.2. Stress Graph in L-Band
The stress history graph shown in Figure 7 presents the measurements of L-bands. Strain gages were installed on the three L-bands at the similar location. The three strain signals showed similar trend and magnitude. The baseline was adjusted at 0 MPa at time zero. The signal increased by about 70 MPa as the band was bended to fit the outer radius of the roll. Therefore, the stress in the band caused by the curvature of the roll was about 70 MPa. The fluctuation of the signal observed in the beginning is attributed to changes in the curvature of the band as the band was manipulated to be properly placed and wrap the roll. At 230 sec, the signal goes up by about 90 MPa because the band buckle was tightly fastened with a pneumatic gun. After the required numbers of L-bands and C-bands were installed, the roll was lifted by an overhead crane. Therefore, at 420 sec, the signal is raised by about 100 MPa which is attributed to the spring-back force of the coil. At 450 sec, the signal is decreased by about 100 MPa because the roll was released to the skid on the ground and the springback force was removed by the weight of the roll. We intentionally cut one of L-bands after the roll was released to the skid. Therefore, at 460 sec, one of the L-band signals was lost. At 480 sec, the roll was lifted again and the signal is raised by about

Figure 6. Tensile specimen for testing band strength.
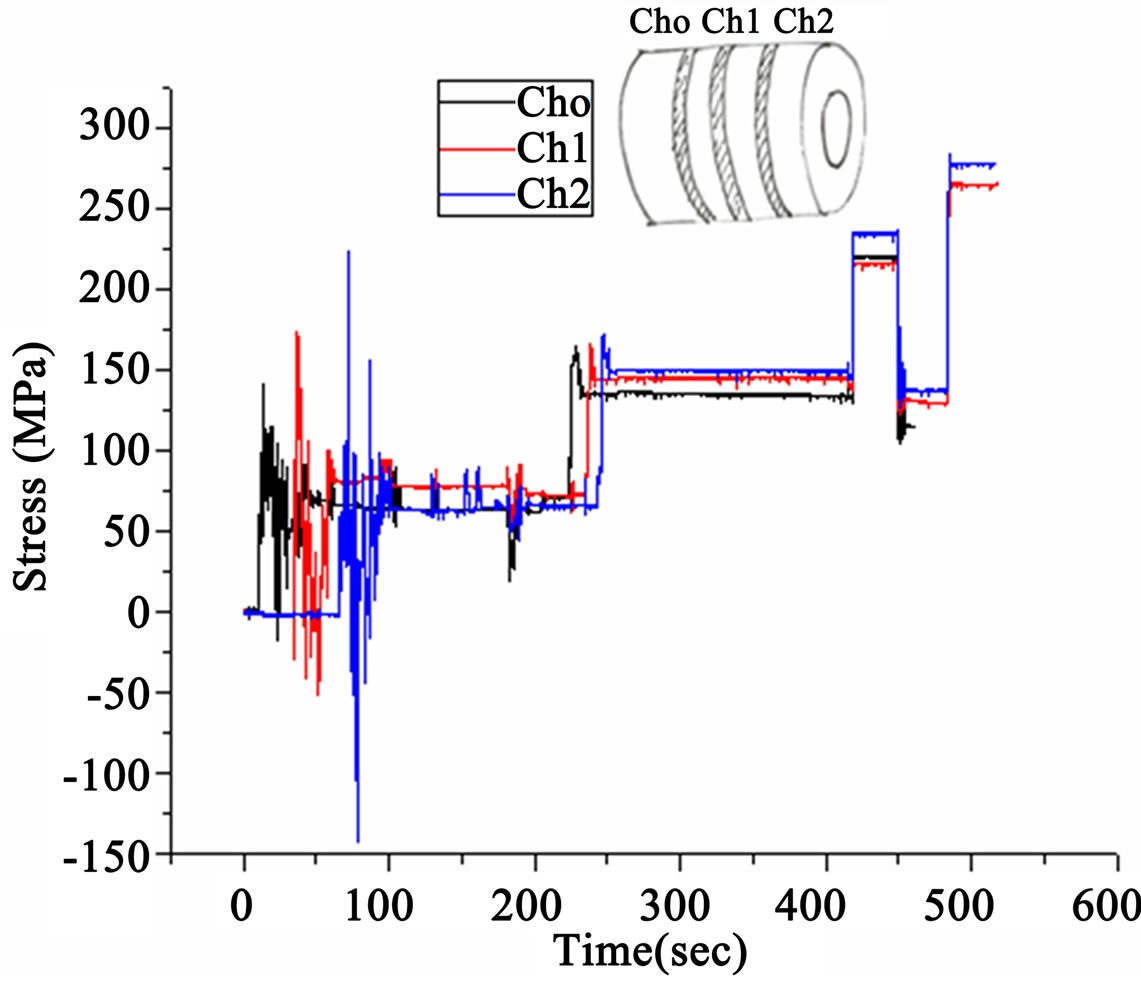
Figure 7. Stress graph in L-bands.
140 MPa, demonstrating a higher springback stress in the band due to a reduced number of bands. The experiment for one roll took less than 10 minutes.
In summary, measurements of stress developing in the L-band were as follow.
Ÿ Stress by curvature of roll = 70 MPa;
Ÿ Stress by fastening of buckle = 90 MPa;
Ÿ Stress by springback of coil = 100 MPa;
Ÿ Stress by springback of coil with one L-band removed = 140 MPa.
The maximum stress was found to lie in the band between the buckle and coil tip (see Figure 4). This is because the fastening force of the band is greatest at the buckle and the springback force is greatest at the coil tip. Therefore, the stress presented in this paper is data obtained from the gage installed at the region of maximum stress.
4.3. Stress Analysis in Tie Band and Estimation of Proportional Constant of Springback Formula
Stress that developed due to the curvature of the band was not taken into account since it had little to do with the failure of band buckles. Twelve coils with different thickness, width, weight, and yield strength were selected for the experiment. Tensile stress caused by the fastening of the band was averaged as 151.7 ± 53.8 MPa. The large standard deviation is attributed to the location of coil tip on the skid. When the coil tip was located near the center of the skid as in Figure 4, the tip was completely pressed by the weight of the roll and the fastening force became larger. However, when the coil tip was away from the center of the skid, the tip was not completely pressed by the roll and the fastening force was not observed to be large. We asked the crane driver to locate the coil tip near the center of the skid as he brought the roll from the production line. However, there were some variations in the location of the coil tip each time.
We observed a sudden increase in the band stress when the roll was lifted after the fastening of the band. This increase corresponded to the springback stress of the roll. The result of the regression analysis between the theoretical formula in Equation (5) and the measured springback stress is shown in Figure 8. The horizontal axis represents the theoretical formula and the vertical axis represents the measured springback stress. The square shaped data plots represent stress obtained for the standard number of tie bands and the circle shaped ones represent stress after removal of one L-band. In Figure 8, the maximum measured springback stress is observed to be around 110 MPa, which developed in thicker coils. If an average fastening stress of 151.7 MPa is added to the springback stress of this coil, the total stress amounts to 261.7 MPa. For thinner coils, the springback stress was much smaller and little contributed to the total stress. Springback stress is observed to significantly increase when one of the bands is removed. It amounts to as much as 180 MPa in thicker coils. The springback stress was averaged to be 33 MPa for twelve coils tested in this study. As one of the L-bands was removed, the average springback stress increased to 79 MPa.
The slope of linear fitting is calculated to be 0.219 with a good correlation coefficient of 0.914. Taking fastening stress into account, a formula for the total stress (springback stress + fastening stress) is obtained as in Equation (6).
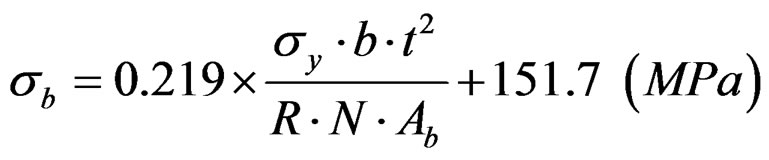 (6)
(6)
Figure 9 shows the springback stress plot with one L-band removed from the roll for the twelve coils tested
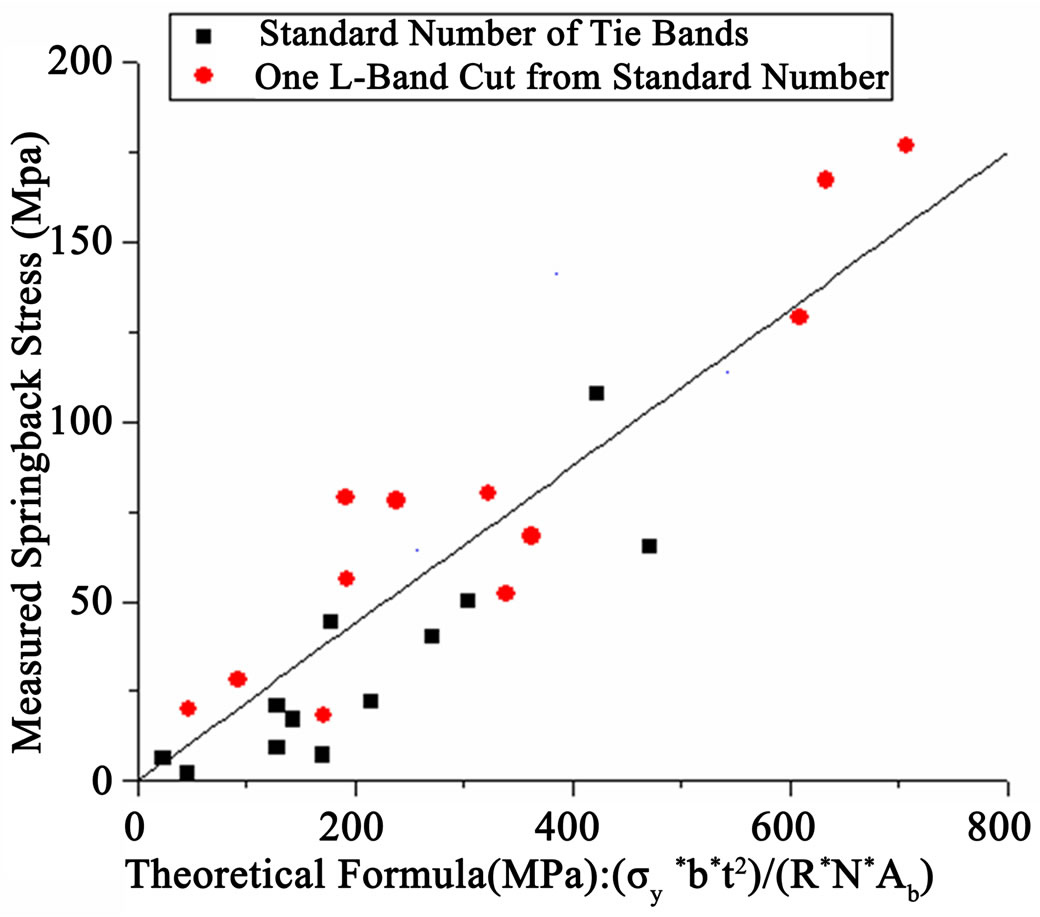
Figure 8. Correlation between measured springback stress and the theoretical formula.
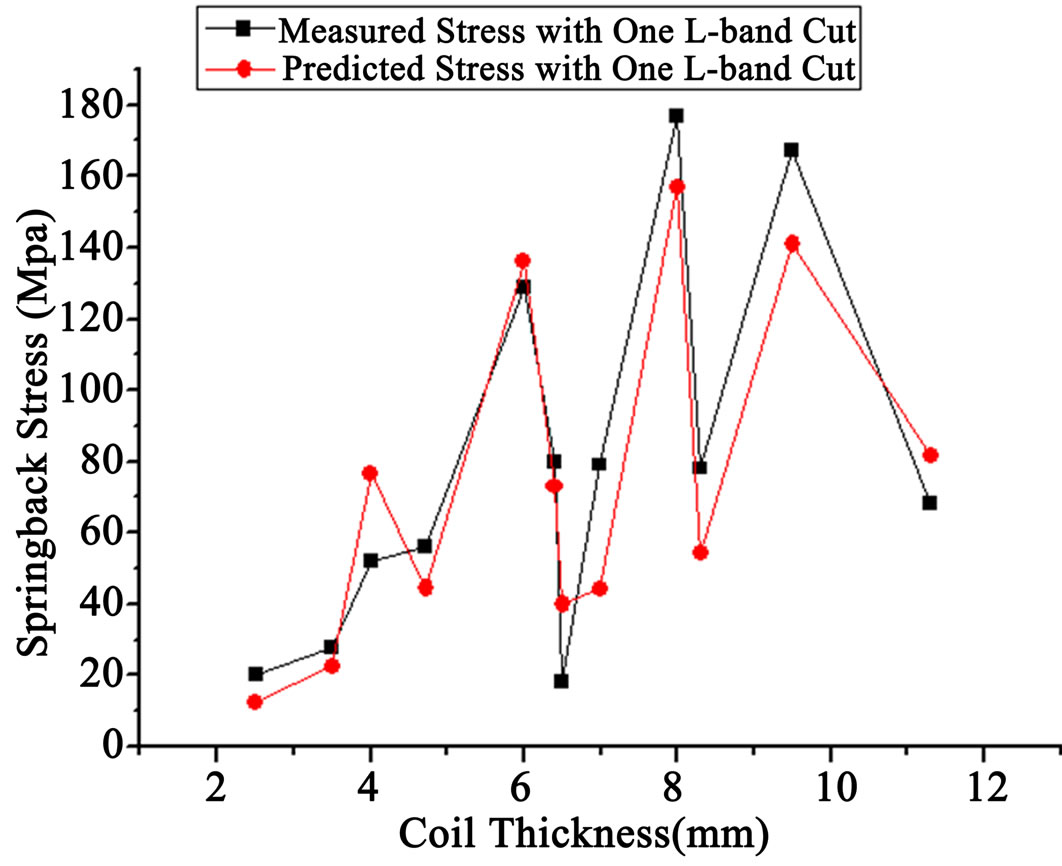
Figure 9. Comparison of measured and predicted springback stress with one L-band removed from the roll for twelve coils tested.
in this study. The square shaped data plots represent measured stress and the circular ones represent predicted springback stress from the first term of the right hand side of Equation (6). The measured and predicted stress show a similar trend in that both stress tend to respond in the same direction as the changes in the magnitude of springback stress. The graph shows that, in general, as coil thickness increases, springback stress increases as well. Fluctuations in the graph are due to variations of other parameters such as yield strength, coil width, roll radius, and roll weight as listed in Table 1. Because of limited access while conducting experiments in the production field, we were not able to isolate the effect of thickness alone from other parameters that influence springback stress.
4.4. Safety Factor
Total stress is obtained by adding stress due to fastening of the band and that due to springback stress as in Equation (6). The safety factor for tie band failure can be calculated by dividing the failure strength, 601 MPa, by the total stress in the band. The average safety factor was found to be about 3.26 for the tested rolls. The lowest safety factor, 1.68, was observed in the 8 mm thick coil with a yield strength of 437 MPa. This coil had a fastening stress of 292 MPa, which was highest among the coils tested, and a springback stress of 65 MPa, which was above the average value of 35 MPa. When one L-band was removed, the average safety factor decreased to 2.60 due to increased springback stress. The lowest safety factor, 1.28, was observed in the same 8mm thick coil. It showed the springback stress of 177 MPa.
We were able to predict the safety factor on the current standard number of bands by using the total stress equation, Equation (6), obtained in this study. When Equation (6) was applied to the POSCO standard [7], the safety factor tended to decrease with increased coil thickness, indicating that thicker coils need more number of bands to avoid excess stress caused by springback of coils.
5. Conclusions
Twelve different coils were tested in the recoiling field to measure stress in the tie bands used to wrap and fasten hot rolled coils. The band buckle showed a tensile strength of 601 MPa which was weaker than the band material strength of 950 MPa. The fastening stress of the bands was averaged to be 151.7 ± 53.8 MPa, which was about a quarter the failure stress of the band buckle. The proportional constant of the springback formula was estimated by comparing the measured stresses in the band with the theoretical formula. The proportional constant was 0.219 with a good correlation coefficient of 0.914, demonstrating a good linearity between measurement and theory.
The springback stress was averaged to be 33 MPa. As one of the bands was removed, it significantly increased to 79 MPa. Adding the springback stress to the fastening stress, the average safety factor of the band was 3.26. It decreased to 2.60 when one of the bands was removed from the roll. The safety factor tended to reduce with increased coil thickness because the factory standard on the number of bands did not significantly take into account of increase in the springback force of the coil with increased thickness.
6. Acknowledgements
This research was supported by POSCO.
REFERENCES
- F. J. Gardiner, “The Springback of Metals,” Transactions of the ASME, Vol. 79, No. 1, 1957, pp. 1-9.
- R. C. Hibbeler, “Mechanics of Materials,” Prentice Hall, Upper Saddle River, 2005.
- K. H. Kim, “Theory and Practice of Thin Metals,” Bando Publishing, Seoul, 1985.
- W. Johnson and T. X. Yu, “On Springback after the Pure Bending of Beams and Plates of Elastic Work-Hardening Material,” International Journal of Mechanical Sciences, Vol. 23, No. 11, 1981, 687-695. doi:10.1016/0020-7403(81)90022-9
- T. X. Yu and W. Johnson, “Influence of Axial Force on the Elastic-Plastic Bending and Springback of a Beam,” Journal of Mechanical Working Technology, Vol. 6, No. 1, 1982, pp. 5-21. doi:10.1016/0378-3804(82)90016-X
- D. G. Alciatore and M. B. Histand, “Introduction to Mechatronics and Measurement Systems,” McGraw Hill, New York, 2007.
- C. S. Lee, “Investigation on Optimum Number of Tie Bands Used to Wrap Hot Rolled Coils,” Project Report for POSCO, Handong Global University, Pohang, 2007.
NOTES
*Corresponding author.

