ABSTRACT

The purpose of this paper is to introduce to you, the Western people, nowadays a “widely unknown” Japanese thermodynamicist by the name of Motoyosi Sugita and his study on the thermodynamics of transient phenomena and his theory of life. This is because although he was one of the top theoretical physicists in Japan before, during and after WWII and after WWII he promoted the establishment of the biophysical society of Japan as one of the founding members, he himself and his studies themselves have seemed to be totally forgotten nowadays in spite that his study was absolutely important for the study of life. Therefore, in this paper I would like to present what kind of person he was and what he studied in physics as a review on the physics work of Motoyosi Sugita for the first time. I will follow his past studies to introduce his ideas in theoretical physics as well as in biophysics as follows: He proposed the bright ideas such as the quasi-static change in the broad sense, the virtual heat, and the field of chemical potential etc. in order to establish his own theory of thermodynamics of transient phenomena, as the generalization of the Onsager-Prigogine’s theory of the irreversible processes. By the concept of the field of chemical potential that acquired the nonlinear transport, he was seemingly successful to exceed and go beyond the scope of Onsager and Prigogine. Once he established his thermodynamics, he explored the existence of the 4th law of thermodynamics for the foundation of theory of life. He applied it to broad categories of transient phenomena including life and life being such as the theory of metabolism. He regarded the 4th law of thermodynamics as the maximum principle in transient phenomena. He tried to prove it all life long. Since I have recently found that his maximum principle can be included in more general maximum principle, which was known as the Pontryagin’s maximum principle in the theory of optimal control, I would like to explain such theories produced by Motoyosi Sugita as detailed as possible. And also I have put short history of Motoyosi Sugita’s personal life in order for you to know him well. I hope that this article helps you to know this wonderful man and understand what he did in the past, which was totally forgotten in the world and even in Japan.

Keywords:

Unknown Japanese Thermodynamicist, Motoyosi Sugita, Thermodynamics of Transient Phenomena, Virtual Heat, Broad Quasi-Static Change, Chemical Potential, Field of Chemical Potential, Diffusion Phenomena, Number of Partition, Dissipation Function, Onsager’s Theory of Irreversible Processes, Prigogine’s Least Production of Entropy, 4th Law of Thermodynamics, Maximum Principle, Pontryagin’s Maximum Principle, Bellman’s Optimality Principle, Theory of Metabolism, Theory of Life, Cybernetics

1. Introduction

Who knows Motoyosi Sugita? Who is Motoyosi Sugita?

The name of Motoyosi Sugita (see Figure 1) is “widely unknown” all over the world today. It is so as well even in Japan nowadays. In this paper I would like to introduce you to this important Japanese theoretical physicist.

I did neither know his name nor his work until this spring in 2016. As I started recently writing a paper on the theory of thermodynamics in the irreversible processes, I found him, this brightest fellow in the early stage of Japan after WWII. Actually he was one of the top figures in the theoretical physicists in Japan right after WWII.

Motoyosi Sugita founded the Japanese Biophysics society as one of the first founding members. To start up the society, in order to show how the scientific society of Bio- physics was important to the Japanese Government, they presented a book on Biophysics as the proceedings of the first meeting among the Japanese Biophysicists [1] . In the part III of this book, Motoyosi Sugita wrote a review, “The Biological Open Systems and Fluid Equilibrium”, where his use of the words “Fluid equilibrium” was meant the so-called “Dynamical equilibrium”. It was his life-time objective to construct “Thermodynamics of life”.

As I read any one of his articles, I have been impressed by his very deep thought on Life as well as Thermodynamics. His ideas seem to me very important and crucial for understanding the physical aspects of life, and therefore, very prompt for making a breakthrough in the research of theoretical biology. Thus, in this paper I would like to summarize what I have studied from his works.

1.1. Birth

Motoyosi Sugita was born in Yatsushiro-machi in Kumamoto prefecture in Japan on August in 1905. Exact day of the born was not known so far. His father was Heishiro Sugita and his mother Haya Sugita. They had the first boy, but the boy was gone by sick before Motoyosi was born. So, Motoyosi became the officially first son of their family. His father Heishiro was the school teacher, later became a principal so that he went many places for teaching as a principal. During Heishiro was spending time at Kumamoto with his mother, Motoyosi was born.

1.2. Education

He graduated from the elementary school attached to the Kochi Teachers College and entered the Dai-ichi Junior High School in Kochi prefecture in 1919.

In 1921 he was admitted to the Konan Junior High School in Kobe, Hyogo Prefecture, moved from the Junior High School in Kochi. At this time most of good high schools in Japan had both junior high school and high school as one school system for 5 - 6 years. The Konan High School was one of them.

In 1926, he graduated from the physical science division in the Konan High School and entered the Department of Physics, the Faculty of Science, the Tokyo Imperial University.

In 1929, he graduated from the Department of Physics, the Faculty of Science, the Tokyo Imperial University. The Tokyo University at that time was under the old system of the Great Empire of Japan, which was totally different from the modern university system of Japan after WWII. Hence, the Tokyo Imperial University was perfectly different from the Tokyo University nowadays. The former was only for the top rank brilliant students selected from them in the Japanese society at that time.

1.3. Working

In 1929, He was enrolled as a researcher at the Institute for Electricity (Denki- Shikenjo), the Ministry of Traffic and Postal Affairs (Teishin-sho).

In September in 1934, he became a teacher at the School for the Japanese Navy Organization.

In August in 1941, he retired the School for the Japanese Navy Organization and became a researcher in Kobayasi Institute in Tokyo (see Figure 2). Here he published his first text book “Thermodynamics New Lecture” in 1942 [2] . He became a lecturer at the Department of Industrial Management, the Tokyo Commercial University.

In March in 1944, he became a professor at the Department of Industrial Man- agement, the Tokyo Commercial University. In April, he also worked as a lecturer at the Tsudajyuku University.

In June in 1949, he became a professor at the Department of Economics, the Hitotsubasi University (see Figure 3). As a concurrent post he became a professor at the Department of Commercial Science, the Hitotsubasi University (until it was re- pealed by the school system change by the Government in 1951).

In September in 1949, he earned the Ph.D. in Science from the Kyoto University by the doctoral thesis “Thermodynamics of Transient Phenomena”, whose partial fulfil- ment was published as a book “Thermodynamics of Transient Phenomena” from Iwanami-shoten in 1950 [3] .

In April in 1953, as concurrent posts, he became a professor at the Department of Sociology, and at the Department of Economics, the Hitotsubasi University. At the same time, he was promoted to be a lecturer for Condensed Matter Physics, at the Department of Engineering, the Meiji University.

In September in 1956, he became a professor both for the Tokyo Commercial University and Hitotsubashi University until it was repealed by the school system change by the Government in 1962.

In April in 1959, he became a lecturer for the intensive lecture for Modern Technology at the Department of Management Sicence, the Konan University and a lecturer for the intensive lecture for the General Commercial Engineering, at the Department of Economics, the Ooita University.

1.4. Marrige

Motoyosi Sugita married Ms. Grace Sakae Oyama in 1933 (see Figure 4). Grace is her Canadian name. She was a Japanese originated Canadian whose ancestry was Christian and immigrated from Hirosaki, Aomori, Japan. She was born in Toronto, Canada. She graduated from the Victoria High School in Toronto. She entered the Nursing School there and graduated at the top of the school. She became the first nurse of the Japanese- Canadians in Canada.

She came to Japan for marriage with Motoyosi Sugita, leaving her family in Canada in 1933. During WWII, she spent very sad time because Japan and Canada became enemy each other, and her family in Canada was forced to be sent to the concentration camps in Canada. Long after WWII, when they visited USA and Canada for attending the International conferences for biophysics and bioengineering, she was able to meet her family members in Canada for the first time in 28 years.

They had one son, Yūkiti. Yūkiti went to Indonesia for his business after Motoyosi and Sakae died. However, he failed his business and he returned back to Japan. He spent his final days in his family’s summer house in Hokuto-shi, Yamanashi, Japan. Yūkiti died on 2 August 2012. Only one relative of Motoyosi Sugita’s family is Ms. Setsu Honda who lives in Hirosaki, Aomori, Japan. Other relatives are now living only in

Canada.

The above information was sent as a letter from Ms. Setsu Honda as her courtesy. I really appreciate it from the bottom of my heart.

1.5. Visits Abroad

In July in 1961, he visited the United States of America and Canada for three months. He attended the 4th International Conference on the Medical Electronics held at New York and the International Conference on Mathematical Biology held at North Carolina.

In August in 1965, he visited the U.S.S.R., Austria, Italy, France, England, West Germany, and Denmark for three months. He attended the International Conference on Molecular Biology held at Napoli, Italy and the second International Conference on Biometrics held at Helgoländ, West Germany.

At the time, he became the president for Bioengineering of the Japanese Society for Medical and Biological Engineering (until 1967).

In 1967, he visited the U.S.S.R., Sweden, West Germany, Netherlands, Belgium, France, Swiss, Austria for three months. He attended the 7th International Conference on Medical Electronics held at Stockholm, Sweden and the 3rd International Con- ference on Biometrics held at Helgoländ, West Germany.

In 1969, he retired from the Hitotsubashi University and became a professor emeritus (see Figure 5).

On the 14th day of January in 1990, he passed away at the age of 85.

1.6. Publications

Motoyosi Sugita published many textbooks [1] - [6] as well as the general books, which were all written in Japanese such as Soceity and Cybernetics [7] , What is Cybernetics? [8] , W. Heitler: Thinking and Wanderings [9] , What is Information Science? [10] , Society and Theory of Systems [11] , Recommendation of Engineering Thinking [12] , The Function of Academics and Creation [13] .

At the same time he published many important scientific papers. Before WWII, he published papers written in German [14] - [21] . After WWII, he published many papers in the Japanese science journals for the public such as Kagaku (meaning Science) and Seibutsu Kagaku (meaning Bioscience) [22] - [35] and Iryo Denshi to Seitai Kogaku (meaning Medical Electronics and Bioengineering) [36] [37] . He published many Japanese articles in his working place reports: in the journal of Kobayasi Institute such as the Bulletin of Kobayasi Institute [38] - [59] ; and in his Hitotsubashi University journals such as the Annals of Hitotsubashi University [60] [61] [62] , Hitotsubashi Ronso [63] [64] [65] [66] [67] , the Bulletin of Hitotsubashi University [68] - [75] . He also published many papers written in English in Western Journals such as the Journal of Physical Society of Japan [76] [77] [78] [79] [80] and the Journal of Theoretical Biology [81] - [91] , as in the references. And also he published many other papers on Physics education and Mathematics education as well, which are neither included nor listed in this paper. You can just see them in the National Diet Library, “Kokkai Toshokan”, of Japan [92] .

1.7. The Research History of Motoyosi Sugita

As early as in 1930’s before WWII, he started to study physics. During this time, at first he seemed to spend much time to translate German physics papers written in Germany (Deutschland) such as Carl Wagner [93] and Georg Siemens [94] into the Japanese and published the articles to the Journal of the Mathematical and Physical Society of Japan (Su-butsu Gakkai Shi). Once he found the concept of the virtual heat, he applied it to the thermodynamics of transient phenomena, and in doing so, he published papers in German in the Japanese journals [14] - [21] .

Thus he seemed to be an expert for the German language in the Japanese physics society at that time before WWII, since in the Japanese education system at that time the Japanese education system had been admirringly adopted from the German system as the first foreign language in the schools in Japan. And surely before WWII, Germany was one of the top countries in sciences including Chemistry and Physics at that time.

Although it has been perfectly forgotten already, Japan was a leading long-time economical supporting country for Germany that was economically totally broken by the WWI. Many Japanese business men privately supported the German society as well. A famous example was Hajime Hoshi who was one of the richest fellows in Japan at that time and he was the founder of the Hoshi Pharmaceutical Company and the Hoshi College of Pharmacy. Hajime Hoshi had supported the Chemical Society of Germany for a long time until Germany would recover [95] up to the era of the Adolf Hitler’s Third Reich of Germany.

Nearly ten years before WWII, Sugita published several famous papers in German as well as in English in the Japanese journals [14] - [21] as mentioned above. However, after WWII his works seemed to be ignored in the Japanese physics society. Because since then, the Japanese education systems totally changed to fit with the English-based society of U.S.A. from the German-based society of Deutschland before WWII. This changed to adopt English as the first foreign language instead of Germany in the schools.

Motoyosi Sugita studied the foundation of thermodynamics for biological systems [2] , and continued it after WWII. From the line of his German physics study which was the top physics country at that time mentioned above, he studied the theory of the German physicists, Becker and Döring [96] and Volmer [97] and an American physicist Frenkel [98] on the cluster growth in the metastable phases in supersaturated vapors.

As early as in 1948 right after the damage of WWII slightly reduced in the society, Motoyosi Sugita published an important paper that discussed the relationship between the metastable (or quasi-static) phenomena in thermodynamics and biological pheno- mena in the Japanese journal, Kagaku [23] . It was also published in the textbook entitled by Thermodynamics of Transient Phenomena [3] .

As the Japanese society was coming back till 1950 he published a more fundamental paper in a Japanese journal, Seibutsu Kagaku [29] . After a long study on the theory of thermodynamics in the transient phenomena such as life, he first postulated that there might exist the 4th law of thermodynamics; otherwise one cannot understand biological phenomena. He stated his considerations on it in §5 entitled by “Can one consider the 4th law of thermodynamics?”. I would like to quote here in the corresponding part from its English version [60] as follows:

…By the way, let us think here the circumstance deeply. According to the 2nd law of thermodynamics, Gibbs’ free energy, G, of the world has tendency to decrease in isothermal and isometric change. On the other hand, we find the tendency that the velocity of decreasing of G, i.e., 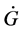wants to take a large value as far as possible. This might be a general principle of nature which I should like to call temporarily the 4th law of thermodynamics.

The foundation of such a large principle will be discussed later, and we can suggest here that it is very important and beneficial idea that the nature of the transient phenomena as well as the living system may be clarified and explained uniformly by this principle.

There are many delicate problems concerning human thought if we propose to clarify the nature of life on the basis of physical and chemistry. In any way the matter looks like as if it were concerned in the 4th law. …

Hence, following the line of thought of Motoyosi Sugita [29] , I can summarize the laws of thermodynamics as follows:

1) The first law (W. Thomson’s principle): The Gibbs free energy G is conserved in a closed system;.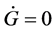

2) The second law (Clausius’s principle): The entropy S always increases in any process;.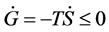

3) The third law (Nernst’s theorem): The entropy approaches zero as the absolute temperature T approaches zero;.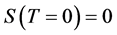

4) The 4th law (M. Sugita’s postulate): The decreasing rate of the Gibbs free energy always takes the maximum in any process; 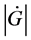= max, where.

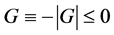Fortunately Sugita published the above paper one year later in English [60] . But it was unfortunate since the journal of the Hitotsubashi university (to which he belonged) that he published was not famous at all among Western physicists as well as the Japanese physicists. And also it has not been available to the public for so long until recently after the internet service was provided.

In 1953 Motoyosi Sugita has found the way to apply the theory of thermodynamics of transient phenomena to more realistic biosystems such as metabolic systems [41] [42] [43] [44] [45] [76] [77] [78] [79] . From this stage his research entered the second stage to construct the thermodynamics of life. Step by step his way of thinking became cybernetics-like, where the feedback control systems played an important role in his theory [46] - [59] [81] [83] - [91] . One of them was cited in Steuart Kauffman’s famous book, The Origins of Order [99] .

Since no computer system was easily available for the bio-systematic calculations in Japan at that time, Motoyosi Sugita collaborated with electrical engineers to construct analog-digital computer circuits for their calculations. They simulated the circuits to obtain the solutions of their-own models of the metabolic control systems. These ideas were summarized as books [1] [5] [6] .

After retiring the Hitotsubashi University, Motoyosi Sugita became to write and publish many general books to the community [7] - [13] .

Although he published many papers and textbooks in science as well as many general books in Japanese, he published only about ten papers in English by unknown reasons. That is why he was so unknown in the Western countries as well as in Japan. Hence, nobody knew him nowadays, and so did I, in spite of his extremely important contributions to the thermodynamics theory.

In this paper I would like to review some important consequences of his theory and discuss the maximum principle in the open non-equilibrium systems as the foundation for the 4th law of thermodynamics to the readers especially in the Western countries.

In Section 2, I will show the bright ideas of Motoyosi Sugita such as the concepts of the broad quasi-static change, the irreversible cycle, and the virtual heat.

In Section 3, I will discuss the Motoyosi Sugita’s approach to the diffusion pheno- mena as the first successful application of his concepts.

In Section 4, I will review the theory of phase change and condensation as a preparation for understanding the following sections.

In Section 5, I will present the theory of thermodynamics of transient phenomena of Motoyosi Sugita, where his theory of chemical reactions will be shown using the concept of the field of chemical potential.

In Section 6, I will show the Motoyosi Sugita’s concept of the maximum principle in the transient phenomena. Here = max conjecture will be discussed, which is a demonstration for the existence of the 4th law of thermodynamics.

In Section 7, I will compare the work of Motoyosi Sugita and those of Lars Onsager and Ilya Prigogine. I hope that the content of this section will be shared with the Western people.

In Section 8, I will discuss the maximum principle of Motoyosi Sugita and that of Pontryagin as well as the Bellman’s principle of optimality. This includes my own theory of the application of the Pontryagin’s maximum principle to thermodynamics. Therefore, I believe that this section is as my emphasis most important among other things.

In Section 9, I will show the Motoyosi Sugita’s theory of metabolism which is the first application of his maximum principle to theory of life. He spent many years as many as 20 years for studying this problem from many sides repeatedly.

In Section 10, I will present the Motoyosi Sugita’s way of thinking on the theory of life. This opens up the thermodynamics of life or life being as well as the network thermodynamics.

In Section 11, as the final section, a simple summary will be made.

2. The Bright Ideas of Motoyosi Sugita

A couple of years after Onsager published his seminal papers on the reciprocal relations in the irreversible processes in 1931 [100] [101] , Motoyosi Sugita published the theory of thermoelectric effects and the Kelvin’s relation in 1933 [17] . This was much later published in Japanese in the Japanese journal during WWII [20] [21] and included in his new text book of theromodynamics, “Netsu Rikigaku Shinko”, meaning Thermo- dynamics New Lecture [2] . In this research he introduced the concept of broad quasi- static change, the virtual heat, and the irreversible cyclic processes in order to describe the irreversible changes in thermodynamics of transient phenomena.

2.1. Sugita’s Concept of the Broad Quasi-Static Change

Motoyosi Sugita [2] [3] meant the quasi-static change “in the broad sense” by the naming of the broad quasi-static change. The broad quasi-static change is defined when the following conditions may be assumed:

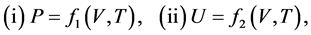(2.1)

where 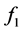and 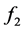are some functions of V and T, respectively.

These are a generalization of the conditions for the case of ideal gases where

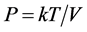and 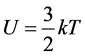are satisfied with k being the Boltzmann constant. When

these conditions are assumed to be satisfied, one can almost follow the standard approach of the quasi-static processes in thermodynamics which means that the process is indefinitely very slow. Indeed, even in the non-idealistic cases the treatment of the quasi-static change in the normal sense has been applied and given plausible results.

This means that the local equilibrium can be satisfied even in the non-equilibrium states, where the broad quasi-static change makes sense if one excludes the relaxation phenomena in which conditions 1) and 2) are not satisfied. Unless the relaxation phenomena are considered, the broad quasi-static change can be applied to most of irreversible processes. The concept of the broad quasi-static change has the amazing possibility of development, once it is combined to statistical mechanics.

Suppose that many macroscopic parts are in the equilibrium state. Let us denote by 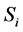the entropy of that i-th small part and by its Helmholtz free energy. The values of the entropy S and the Helmholtz free energy F of the whole system are given by

(2.2)

Therefore, if we use

(2.3)

then we have

(2.4)

This means that when one considers the broad quasi-static change in the irreversible processes, one should not take or need not take the W or Z over the entire phase space. One must cut off the phase space into the small pieces that are in local equilibrium, and concatenate them to cover the whole phase space. This is the meaning of the local equilibrium in the point of view of Motoyosi Sugita.

2.2. Sugita’s Concept of the Virtual Heat

Another assumption that forms the theory of irreversible processes is the concept of the virtual heat. Let us consider the case when the heat ejected from the reservoir that is outside the system. Let us suppose that the reservoir follows the same change of the broad quasi-static change as the system under consideration. Let us denote by the heat absorbed by the thermodynamic system and by T its temperature. Let us assume that the origin of the irreversibility lies inside the system and consider the friction inside the system. Then,

(2.A)

is satisfied, where is the change in the internal energy and is the work to do the outside system. If we consider the expansion of the piston-cylinder system,. Suppose that there exists the friction between the wall of the cylinder and the piston and suppose that the work is consumed by the friction. Now we have

(2.5)

Substituting Equation (2.5) into Equation (2.A), we obtain

(2.6)

This is the virtual heat defined by Motoyosi Sugita. The left hand side of Equation (2.6) is nothing but the heat of the system. Therefore,

(2.7)

where

(2.B)

Now, from the concept of the broad quasi-static change, must have the in- tegration denominator as

(2.8)

Here we never think as if

(2.9)

holds true.

If we think of the adiabatic change without input and output of heat, i.e., , then

(2.10)

Hence,

(2.11)

What is important here is the distinction between and and that between Equation (2.A) and Equation (2.B).

In Equation (2.5), if the work is consumed and become the heat outside of the cylinder, then for the inside of the system (e.g., the gas)

(2.12)

For the outside of the system, the reservoir gives the heat to the gas system and at the same time it receives as a heat the energy lost from the system by the work. Hence,

(2.13)

Therefore, for the whole system we have

(2.14)

Thus, the Sugita’s concept of the virtual heat is very natural and important when one considers the thermodynamics of transient phenomena.

2.3. Sugita’s Concept of the Irreversible Cycle

Let us now consider the Sugita’s concept of the irreversible cycle. Let us denote by the lowest possible temperature available of the thermal reservoir. Let us denote by the entropy change of the reservoir with temperature and denote by its lost heat, in the course of the process when the irreversible cyclic process is preformed. Then we have

(2.15)

since the reservoir gives the heat to the system.

Let us denote respectively by T and S the temperature and the entropy of the system (working material) that performs the cycle. Then we have

(2.16)

since the system receives the heat in addition to the virtual heat of the process, where. Hence, for the whole system, we have

(2.17)

After finishing the cyclic process, the system has to come back to the initial stage of the process (i.e., the initial condition) such that it yields

(2.18)

Hence, the total entropy change in the cycle is given by

(2.19)

On the other hand, for reversible processes, since

(2.20)

one has

(2.21)

Thus, the entropy change occurs only in the thermal reservoir outside the system in the process of the irreversible cycle, such that Equation (2.18) cannot conflict with the second law of thermodynamics. The equality of Equation (2.18) has a great meaning

that the integration of vanishes when the path is closed around the course of the

irreversible cycle. Therefore, one can treat quantitatively the thermodynamics of the irreversible cycle in the same as that of the reversible cycle.

I would like to note that this aspect of the Sugita’s concept of the irreversible cycle is different from that of the Prigogine’s concept of the irreversible cycle, where the entropy change of the system is treated as a quantity that always increases during the process such that (in their notation) [102] - [112] . This is the consequence of what they never consider the irreversible cycles.

Now let us consider the change in the thermal reservoir. The heat is ejected to the system. Therefore, its entropy change is given by

(2.22)

since is the heat adsorbed by the reservoir. Here the quantity has been

called the reduced heat. However, the reduced heat is not a real heat for the reservoir, since the sign of it is reverse to that of entropy of the reservoir [Equation (2.22)]. Thus, although the concept of the reduced heat plays a historical role, it is not so important as a physical quantity. From Equation (2.19) together with Equation (2.15) the following holds

(2.23)

This is nothing but the Clausius’ inequality for the irreversible cycle, where the equality holds true for reversible processes. This can be regarded as the generalization of the standard proof for the Clausius’ inequality for the irreversible cycles [2] [3] [4] [113] .

Historically speaking, Clausius accomplished to derive this relation for the first time. From the fact that the equality holds true in the reversible processes, he showed that

becomes an exact differential and then he derived the entropy. In his approach he

represented a closed curve representing any thermodynamic cycle by a staircase with adiabatic curves and isothermal curves. Regarding the cycle as a combination of many infinitesimal Carnot cycles, for the high temperature sources, denote by and the high temperature and the received heat of the n-th thermal source, respectively, and for the low temperature sources, denote by and the low temperature and the eject heat of the n-th thermal source, respectively. Taking into account the sign of each heat, he proved the relation by using

(2.24)

Now if the intervals could be made so as to be infinitesimally small, then Equation (2.24) becomes

(2.25)

This is the Clausius’ inequality derived from himself [113] .

However, once we look at the expressions in Equation (2.24), the sign of the reduced

heat or is opposite to that of the entropy of the thermal source. In the

quasi-static reversible processes it becomes exactly the entropy change of the working material and hence the equality of the above Equation (2.25) can hold. From this situation, usually it has been thought that one cannot treat the theory quantitatively since the inequality holds in the irreversible processes or when one seeks for the

entropy by, must be the heat received under the reversible process. It is

because one escapes from the complexity of the irreversible processes such that one need not take into account the working material, and because one discusses the cycle process only considering the lost heats. On the other hand, although not always but when the process can be regarded as the broad quasi-static change, and when the true character of the virtual heat is clearly known such as the friction heat or thermal conduction, we can take instead of. And as discussed in the above, even in the irreversible processes we can define the entropy by Equation (2.17) and can use the equality Equation (2.18) as well.

Since the state goes back to the initial state after the completion of the cycle, it seems trivial that the entropy goes back to its initial value as well. Since it was said that in the irreversible processes, one cannot say anything about the entropy in the midst of the process, we could not have said anything about like the above. Now we should note that is neither obtained by ignoring the irreversibility nor is given by intentionally regarding the system as being reversible.

In order to derive the entropy, one must consider the quasi-static reversible processes and define the heat of the processes in the standard point of view as usual. But once one defines the entropy under the quasi-static change, one can use the relation in the broad quasi-static change, whether or not the process is reversible or irreversible. This point seems to us neither clear nor emphasized in the standard texts. In other words, the distinction of the use of and is not thorough according to one's needs. That is, if one takes then the inequality of Equation (2.23) holds; if one takes then the equality of Equation (2.18) holds. One can generalize the above argument to the more general cases such as the case when there exists the thermal conduction in the working material as well as the case when the thermal temperature is not uniform.

This is the argument of Motoyosi Sugita for the concepts of the broad quasi-static change, the virtual heat and the irreversible cycles in the thermal processes. He applied these concepts to the various physical systems such as the thermoelectric effects of Lord Kelvin [2] [3] [4] [14] [15] [17] [20] [21] as well as many biological systems [38] - [91] .

2.4. Application to the Kelvin’s Relation in the Thermoelectric Effect

As an application of the above results, we become able to treat the problem of thermoelectricity (see Figure 6), which had been thought to be difficult to consider. Now, let us denote by (1) the high temperature part with the temperature and by (2) the low temperature part with the temperature [3] . Denote by the heat ejected from (1) and denote by and the heats dissipating in wire A and B, respectively.

Seeing from the outside of (1), the ejected heat per second is given by

(2.26)

Next, let us denote the resistance by. The Joule heat (regarding the virtual heat) due to the electric current is. Therefore, the heat that this part actually absorbs per second is given by

(2.27)

This is the so-called Peltier heat. If we take as the propotional constant, then. Therefore, we now have

(2.28)

For the part (2), we similarly obtain

(2.29)

where the minus sign in the left hand side comes from the reverse direction of the current i in the circuit.

Next consider the part in the wire A. Define by W the heat that is conducting the wire and flowing in the part and define by the heat that is conducting the wire and flowing out the part. Denote by the heat emitted from the part to the surroundings. Denote by its resistance of the wire A. Then, the heat that this part absorbs is given by

(2.30)

This is coreesponding to the quantity. This is called the Thomson heat, where is a constant, the temperature difference in this part.

Similarly for the wire B and considering the part, we obtain

(2.31)

where the sign in the right hand side is due to the condition that the direction of the temperature is reversed to the direction of the current i.

In the stationary state, the sum of the heats that this system absorbs equals the work that the electromotive force E can do. Hence, one has

(2.32)

which is the equation corresponding to the relation (2.B) but its integrated form, where the integration of corresponds to. On the other hand, the equation cor- responding to the relation (2.A) is given by

(2.33)

Next, suppose that the relation (assuming) of Equation (2.8) holds, where in order to satisfy the relation (2.B) the assumptions of (i) and (ii) are necessary. For (i), it is easy for u to satisfy. But for (ii), it cannot be easy for P to compared with the electromotive force in equilibrium. Therefore, we assume instead of (i) for the foundation for the proof. By this, we obtain

(2.34)

It is obvious when the thermoelectric couple is in the stationary state. Then the entropy change occurs only in the thermal reservoir (or one may think the one-round of electron through the circuit as a cycle.) From Equation (2.32) and Equation (2.33), the Kelvin’s relation is given by

(2.35)

So far we are based on the Clausius’ inequality:

(2.36)

Now, rewriting, , , ,

(2.37)

The derivation of the above result Equation (2.37) is as follows: Denote by the cross sections of the wires A and B and by and the thermal conductivities of the wires A and B, respectively. Using the above notations, we first hold the following relations

(2.38)

(2.39)

(2.40)

For the wire A we find

(2.41)

By integration by parts we obtain

(2.42)

On the other hand, for the wire B we similarly obtain

(2.43)

(2.44)

respectively. Here we think that and are included in the sums of and.

Therefore, based on the inequality (2.37), one cannot derive the Kelvin’s relation, as long as the thermal conduction and Joule’s heat can be neglected. Namely, to take Equation (2.37) as the base is not wrong but not sufficient [3] . As Boltzmann [114] had shown the following relation

(2.45)

this cannot exactly yield the Kelvin’s relation.

Now, from Equation (2.36) the linear term of becomes zero. That is,

(2.46)

This means that if Equation (2.36) is added a small quantity less than 0, then Equation (2.37) forms an inequality. Therefore, it is obvious that one cannot derive the desired result from it. On the other hand, we obtain Equation (2.36) by not only considering the heat flowing in from the outside of the system but also considering the heat that the system absorbs. And by this we can derive the Kelvin’s relation exactly.

In summary, the point of view of Motoyosi Sugita lies in the fact that one can obtain Equation (2.36) even for the irreversible cycles. Now, the entropy increase can be obtained immediately from Equation (2.46). Motoyosi Sugita [2] [3] [4] [20] [21] pointed out the insufficiency of the Tolman’s argument [115] in the same problem.

3. Sugita’s Approach to the Diffusion Phenomena

Let us next consider the Motoyosi Sugita’s approach to the diffusion phenomena [3] . In order to see how the concepts of the broad quasi-static change and the virtual heat work in each physical problem, he applied them to the diffusion problem [3] . The diffusion phenomena are really important phenomena when we construct the theory of thermodynamics in transient phenomena. To do so, I would like to follow his argument in his test book [3] .

3.1. Langevin Equation

Now let us consider an ideal gas that is constructed from the mixing of the two species of molecules 1 and 2. For the sake of simplicity, we assume that the density gradient only exists in x direction. This is equivalent to consider the one-dimensional diffusion problem along x direction.

Let us denote by the mass of each molecule of species 1 (species 2). Let us denote by () the number of molecules per cm³ of species 1 (species 2) which have the velocity along x direction. The mass of species 1 that passes the interface of 1 cm³ piercing x in a second is

(3.1)

Hence,

(3.2)

Now, let us denote by, the mole numbers per cm³ of molecules of species 1 and 2. We have

(3.3)

where, the Avogadro number. We now have

(3.1’)

Or if we use, , , then

(3.1’’)

Now taking as and if one can ignore the shift of the center of gravity due to the diffusion, then from Fick’s law, one can obtain

(3.4)

where. On the other hand, if it cannot be ignored then one has to put the viscous term of the fluid. If we put as

(3.5)

then the above equation looks like the Langevin equation type such as

(3.6)

So far we have considered the case of ideal gases. However, for more general cases, if we use

(3.7)

the right hand side of Equation (3.6) can be rewritten as

(3.6’)

or if we use then we can rewrite as

(3.4’)

As Sugita pointed out, the Langevin equation is the equation of motion that one thinks as if the stationary motion is considered statistically so that the effect of accele- ration cannot play a role to the averaged velocity, and the random forces come from like-particles in thermal motions are statistically averaged.

Next let us explain that when the work done by the resistance of friction is added to the system as the virtual heat, the increase of entropy by this process becomes that of entropy by the mixing of the molecules of species 1 and 2.

3.2. Mixing Entropy and Free Energy

Now let us denote by the density of the molecule of species i at each point x in the midst of the mixing process. And let us denote by the number of the molecule of species i at each point x in the midst of the mixing process such that, where. Assume that the chemical potential (per mol) for each component of i, , is given as

(3.8)

where is assumed to be constant in the system. Then, the Gibbs free energy of the entire system should be given as

(3.9)

If the equation is reversely seen, then the chemical potential has to be defined by

(3.10)

Now, since the G is decreasing by the mixing, from Equation (3.9) we have

(3.11)

This means that in the mixing system of ideal gases, the mixing entropy is increasing by the mixing of the molecules and by it G is decreasing. And although the decrease of G is the decrease per second in the irreversible process, we cannot necessarily know but surely know the change in time of G in the midst of the process.

Based on the Langevin equation Equation (3.6'), suppose that the molecule is forced to move by and it transports against the friction. Suppose that we can regard the friction the virtual heat and therefore the entropy of the system can increase by the virtual heat.

For the sake of simplicity let us limit ourselves to the ideal gases. Then, only the energy per molecule is given as a heat per second from the virtual heat. This amount of the quantity per volume becomes. For the whole system it provides only the heat that is defined by

(3.12)

If we assume the process is an isothermal change, then replace by Equation (3.6'). We have

(3.13)

The first term in the right hand side vanishes if the boundary condition is taken. In the second term in the right hand side, since we have the continuity equation:

(3.14)

if we change as in Equation (3.1'), then Equation (3.13) can be represented as

(3.15)

On the other hand, in the ideal system the change in G only occurs in the change of entropy. Therefore, if we rewrite as, then we obtain

(3.16)

Hence, this agrees with Equation (3.11). From considering the above situation, we can recognize that the assumption that the force acting on the diffusion particle is given by Equation (3.6’) is not inconvenient.

Let us consider the case of the non-ideal systems [28] . In this case the chemical potential becomes density dependent. And in the case of the isothermal and isobaric mixing, the volume change and the flow in and out of the heat can occur. And therefore the entropy change is no longer given by that of the ideal mixing,. For this time, Equation (3.9) and Equation (3.11) hold true and the entropy increase due to the receive of the virtual heat is given by Equation (3.15) as well. How can one interpret this? The mixing entropy in this case can change since there occurs the thermal heat exchange other than the virtual heat. If temperature T and pressure P are kept constant, and if the work done for the outside of the system is given by and the change in the internal energy is given by, then the input and output of the heat is given by

(3.17)

Therefore, once we add the heats due to Equation (3.15) and Equation (3.16) to the above increase of entropy due to, we find

(3.18)

This is not inconsistency but rather everything is consistent very much. If we compare the above with Equation (3.16), then

(3.19)

This means that occurs by (). Thus, even for this case of non-ideal gases the entropy increase due to the friction by the mixing can be regarded as the heat receive from the virtual heat source. This is also thermodynamical support for the phenomenological construction of the theory where the quantity such as can be regarded as a field. Motoyosi Sugita called this approach the Onsager-Meixner- Sugita’s method [3] .

3.3. How to Count the Number of Partition

For this title, Motoyosi Sugita used the word the number of complexion. The number of complexion is nothing more than the number of partition in classical statistical mechanics or the number of sates in quantum statistical mechanics in the modern terminology [116] [117] . When the system is in equilibrium, the number of ways that particles interchange their positions in the system is nothing but the number of complexion in his terminology. In this equilibrium case, one can definitely define the chemical potential such as Equation (3.8).

Can such a treatment be allowed even in the midst of the non-equilibrium process? This was the Motoyosi Sugita’s problem. Obviously, it is allowed for the equilibrium state of the process. But it is not trivial for the non-equilibrium state in the irreversible or transient phenomena.

Suppose that the previous argument that provides Equation (3.8) is correct [28] . Assume that is constant. Then one finds

(3.20)

where, the gas constant and the Avogadro number. Or regarding the above integral for as the sum over, we can rewrite it as in a different form:

(3.21)

Hence, by taking the functional derivative for the above with respect to, the chemical potential is given by

(3.22)

The second term in the right hand side comes from the mixing entropy of the system. Therefore, it corresponds to what one assumes that the number of partition at an instantaneous time in the midst of the process is given by

(3.23)

If we take, then since and, Equation (3.22) is derived directly. Therefore, the meaning of is the partition number that is considered within the local part of.

Now, suppose that the whole region of space is divided into small parts of and that the molecule traffic between the small parts is assumed to be forbidden. In the time-interval of for the irreversible process, each part accomplishes its local equilibrium with the concentration, which means that the concentration of the i-th molecule at within, such that the number of partition is given by Equation (3.23) and G is given by Equation (3.21). Corresponding to this state, some region in the phase space has to be considered statistical mechanically.

Next, if we remove the partitions and wait for a short time so that the diffusion occurs, and if we place the partitions in the system once again, then the distribution of the molecules becomes different concentrations of from those before, since the diffusion mixes molecules within such a short time. And the system becomes a new local equilibrium since the partitions are entered in the system. If we looked at the corresponding area in the phase space, then it would move to the position slightly away from the previous one as long as the time interval is very short.

In this way, as the distribution of concentrations is continuously changing by the diffusion, the corresponding region in phase space is also moving continuously through the region corresponding to each state in the midst of the irreversible process and going into the region corresponding to its final equilibrium state. Once the true equilibrium is achieved, not changing or mixing the molecules within the region but the changing or mixing the molecules in the entire space becomes necessary. Hence, the number of partition for the entire system has to be calculated in equilibrium.

There is no limit for time in the equilibrium state, since each process is reversible so that an infinite time can be spent. Therefore, even if molecules are far apart to each other, the state that the molecules exchange their positions can be realized by the ergodic assumption. When the diffusion occurs, at each point can change continuously in time. If is fixed at some moment, then for such a short time the molecules within can exchange their positions and the macroscopic mixing state in the so-called relaxation time can be realized. The above result supports this sort of consideration.

In other words, the molecules within are jumping the positions ceaselessly one after another and transporting microscopically different states by thermal fluctuations. Considering this situation for the phase space, we think that the representative point is doing the Brownian motion within the limited partial region of the phase space and for the time interval considered above it is wandering each point in that region. This approximation would be a rough approximation than the request from the ergodic assumption. But it wanders to the extent that the macroscopic state near the equilibrium state can be realized. Hence, the number of partition is calculated within this region such as Equation (3.23). Thus, if we explicitly describe this, then with gradually shifting the region where the Brownian motion is carried out, the region is going to expand, and finally becomes an extremely broad region that corresponds to the equilibrium. Although this speculation must be justified statistical mechanically [118] [119] , it is required from the macroscopic argument inevitably.

On the other hand, for each diffusion molecule, it should not move with the constant velocity in Equation (3.6') but the central point of the molecules moves with each molecule following the Brownian motion. In many molecules there are higher speed molecules and the lower speed molecules at the same time, and even there exist molecules that reverse their motion. The averaged velocity among such molecules like the molecule of species 1 is given by. In the same way, the chemical potential is meaningful as an averaged value per molecule. This is related to. Thus, we consider the averaged quantities without considering each motion of the molecule such as the kinetic theory of gases. Although it is a phenomenological theory, in order to generalize the treatment of complex statistical mechanics kinematically and to relate it to thermodynamics, there exists nothing else so far.

In summary, the above argument is the Motoyosi Sugita’s argument on the application of the concepts of the broad quasi-static change and the virtual heat to the diffusion phenomena [3] . He also applied his brilliant concepts to many other systems such as the osmotic pressure for the cell membranes. However, I would like to skip this here.

4. The Theory of Phase Change and Condensation

Before going to discuss the Motoyosi Sugita’s theory of thermodynamics of transient phenomena in detail, let us look at the theory of nucleation or condensation in 1930’s [96] [97] [98] as an excursion.

His theory was motivated to be apply it to construct the thermodynamic theory or thermodynamics of life or life being [3] . In order to construct thermodynamics of life or life being, he presented mainly three big concepts:

1) the “field”of chemical potential;

2) the generalized nonlinear Ohm’s law;

3) the maximum principle in transient phenomena.

He extracted these concepts from intensively studying the theory of phase change and condensation or nucleation originated by the German physicists, Becker and Döring [96] and Volmer [97] and an American Physicist, Frenkel [98] before WWII. Therefore let us first review some of the early theory of nucleation phenomena as a prototype or precursor of the theory of thermodynamics of transient phenomena of Motoyosi Sugita.

4.1. Frenkel’s Theory on Nucleation in the Supersaturated State

When Mayer [120] studied statistical mechanically the nature of vapor, he considered clusters that are aggregated into groups of several molecules in addition to single molecules. Frenkel [98] simplified this idea to phenomenologically represent such groups of several molecules as spherical clusters with a certain radius.

Let us now denote by (n) a cluster with n molecules. Denote by its free energy. Let us define by the chemical potential per molecule in the liquid state. Let us define by the surface energy per area of a small drop whose radius is defined by r. In this setting, the free energy of the drop with radius r is given by

(4.1)

If we define by the number of molecules in 1 cm³ in the liquid state, and if we write as

then

(4.2)

Next, define by the number of (n) (n-clusters) in the vapor and we define as

(4.3)

then the Gibbs free energy G of the whole vapor is given by

(4.4)

where T is the temperature of the system, k is the Boltzmann constant. Here is the chemical potential for a single molecule in the vapor and the second term in Equation (4.4) comes from the mixing entropy of the molecules.

When the mixing entropy between single molecules and clusters with different sizes should be evaluated, the expression of mixing entropy for molecules of identical sizes is assumed and used to this case. This seems a problem. And as n becomes large, the expression for the mixing entropy must be modified. Furthermore, we cannot imagine that big liquid drops can float in the vapor. Therefore, the above expression of the Gibbs free energy is not exact quantitatively. However, if we restrict ourselves to the phenomenological argument, then it seems sufficient to approximately represent the system by Equation (4.4).

On the other hand, let us denote by the total number of molecules in the whole system. We now have

(4.5)

Suppose that this mixture of clusters in vapor lies in equilibrium. In this case, seeking for the maximum of G with taking the variations of and, we obtain after some manipulation

(4.6)

or

(4.7)

This is the equation that determines the distribution of (n)-clusters first derived by Frenkel [98] .

This is the distribution of concentrations of (n) clusters in the equilibrium state in the saturated and the supersaturated vapors. It means as follows: When some part of the gas conforms the mixture of (n)-clusters and when the mixture is included in the system, the entropy becomes larger than the one when all the molecules stay as single molecules in the vapor. If we look into each molecule, means that due to the effect of surface energy, the free energy of (n) cluster, , is larger than, n ´ the free energy of each single molecule. However, if we look into the system as a whole, then the free energy of the whole system may be lowered by the mixing entropy of the distribution of the clusters of various sizes. Statistically speaking, the probability that the system lies in a state that groups of (n)-clusters are mixing exceeds the probability that all molecules remain to be single molecules.

4.2. Supersaturated Vapors

Next following the argument of Frenkel [98] , let us consider the supersaturated vapor. When the vapor is supersaturated, since, from Equation (4.1) we obtain

(4.8)

where if we denote by the number of molecules in 1 cm³ in the liquid phase, then is given by

(4.9)

Considering Equation (4.8), as n becomes large, becomes negatively large. Therefore, according to Equation (4.6) it results in that there exist only the clusters of large n. This means that an infinitely large singe cluster exists in the vapor. Hence, it is nothing but the liquid phase.

Thus one can understand the behavior of the supersaturated vapor system pheno- menologically. If, then both the vapor phase and the liquid phase are in equilibrium and the system is a supersaturated vapor; If, then the system is a heating liquid; If, then the system is stable for a liquid phase. However, since the changeover is disturbed, the system has to transiently exist as a vapor, i.e., the gas phase, which is the supersaturated vapor. If one treats the system as being in equilibrium, then one obtains the result of the liquid phase only. So, the supersaturated vapor phase has never been obtained by the standard approach of equilibrium thermodynamics.

Motoyosi Sugita pointed out the following [3] [23] : As stated in the previous section, one can assume that even in the transient phenomena, the expression of in Equation (4.7) holds true and one can apply the to the expression for the Gibbs free energy G using Equation (4.4) in the midst of the transient phenomena. This means that one cannot take the partition number over the entire space. If we do such a thing, then the supersaturated state never appears theoretically, as mentioned in the above. In this case we are considering of cutting off the clusters larger than a certain size and freezing the present temporarily.

Now, the cause that interrupts the changeover from the vapor phase to the liquid phase is the lack of the surface area which leads to the condensation. In order that the liquid phase emerges in the supersaturated vapor phase, it has to pass through the state of extremely small liquid drops in the midst of the process. Large clusters are not included in the midst of the growth. Very small is the rate that clusters gradually grow as the condensation occurs at the surface of small (n) clusters. Therefore, the system is at a standstill as a vapor. According to Frenkel [98] , this is the metastable state. The distribution of with small n reaches the equilibrium and it is described by Equation (4.6).

Motoyosi Sugita noted here the following: When the Gibbs free energy for the entire system G is decreasing as the second law of thermodynamics shows, there appears some part which has larger Gibbs free energy, and this supports the place where con- densation occurs, and it determines the rate of the change in the transient phenomena.

The reason why clusters have large is due to the fact that the arrangement of molecules is very crowded almost same as in liquid, while the position energy between molecules is larger than that in the part of the same volume in the normal liquid. It has a small entropy corresponding to the order of the arrangement, which is also important when we consider life or life being. While n is smaller than some size of nuclei, since there exist the intermolecular forces, the probability that n molecules get together to make a group of n molecules is much larger than the probability of the chance of n-tuple collisions of molecules in an ideal gas where molecules move freely. This is also important when we consider life or life being. It states that when the volume of phase space, that is, the thermodynamical probability, corresponding to the existence of a complex coacervate (the phase space when we consider only the molecules that con- struct a coacervate) is small enough, its entropy is also small correspondingly.

Next, let us differentiate Equation (4.8) with respect to n and evaluate the maximum.

Substituting the value of into it, and taking where is the density of

the liquid, M the molecular weight and is the Avogadro number given by, respectively, we have

(4.10)

On the other hand, let us denote by the pressure of the saturated vapor over the horizontally flat interface and by p the pressure of the supersaturated vapor. Now we have

(4.11)

From this we find the Kelvin’s equation:

(4.12)

And if the maximum of is taken as, from Equation (4.10) we obtain

(4.13)

where K is the maximum size of the clusters. According to Frenkel [98] , the cluster of this size is the nucleus of condensation. The range that is increasing as n is increasing is the region of. At the saturated pressure p in equilibrium with nuclei is equal to the supersaturated pressure. Hence, (due to the fact that becomes the maximum) the unstable equilibrium is realized between the small liquid drops which becomes the nuclei and the vapor. Here it is not until many clusters exist in the vapor that the clusters can become in equilibrium with single molecules in the vapor. In the nuclei only one nucleus can keep equilibrium although it is unstable.

In the above argument, we have assumed that in the metastable state the rate of growth of cluster is small enough. And although the system is not in equilibrium, we have treated it as if it were in equilibrium. This provides the variation principle. This led to the distribution of clusters that is given by Equation (4.6) or Equation (4.7) for n small. Let us next discuss the rate of cluster growth in order to understand the essence of the metastable (quasi-static) state or the transient state. This concept seems common in fundamental aspects of the problem when we consider ther- modynamics of life or life being, although theoretical appearance seems rather different.

4.3. Kinetics of Cluster Growth

According to Becker and Döring [96] , the growth of the cluster is carried out in the following process:

(4.14)

Here 1 stands for a single molecule and it collides with (n), the cluster consisting of n molecules and condensates into, the cluster consisting of molecules. Although there may exist possibly many other process such as

(4.15)

and so on, the probability of these processes must be very small enough compared with that of the collision process of Equation (4.14), since triple collisions or the collision between (3) and 1 are molecular dynamically very few events such that they loose the meaning to form. Thus, in the kinetics or the rate theory one has to pick up the rate-determining process only, while one ignores the other not-rate-determining pro- cesses. This way of thinking is also helpful when we investigate the life phenomena.

Volmer [97] slightly improved the calculation of Becker and Döring [96] . In his calculation he denotes by J the rate of the process of Equation (4.14), which is the total number of clusters per time from 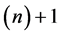to. Then he writes it as

(4.16)

where is the number of the clusters of (n), is the condensation rate per unit area, and the evaporation rate per unit area and means the surface area of sphere with the radius which is given by the sum of the radius of cluster (n) and the radius of a single molecule.

Now in equilibrium of the growth process, both the forward and backward processes are attained such as

(4.17)

This provides. From Equation (4.16) together with this condition, it yields the following relation:

(4.18)

where N is the total number of molecules in the system such that. This can be also derived directly by applying Equation (4.6) to and. Hence this is nothing but the law of mass action for the chemical process of Equation (4.17).

In the saturated vapor, it is no wander that Equation (4.18) must hold valid as well. However, even in the supersaturated vapor, the rate J is expected to be small such that. Therefore, in the latter case we expect that both Equation (4.17) and Equation (4.18) hold valid approximately. This is very important when we consider the transient phenomena in the stationary state. On the one hand there exist main processes and under current processes, on the other hand the processes of and are performed and the equilibrium between them is attained. This point is very important when we investigate the dynamic equilibrium.

In summary the above theory is the theory of condensation in the supersaturated state originated by Becker and Döring [96] and completed by Volmer [97] and Frenkel [98] in the Western countries before WWII.

4.4. Thermodynamics of Kinetics of Cluster Growth

Motoyosi Sugita investigated the above theories of Becker and Döring [96] , Volmer [97] and Frenkel [98] very carefully.

In considering the kinetics of the cluster growth thermodynamically, since the half of Equation (4.18) could be valid even for the non-equilibrium state and then it holds as well, he rewrote Equation (4.18) as follows:

(4.18’)

Denote now by and the concentration of cluster (n) and the

concentration 1, respectively. Then J is given as

(4.19)

Let us introduce the concept of the chemical resistance such as

(4.20)

and let us define the chemical potential for a single molecule in cluster (n) in the midst of the growth process by

(4.21)

Then Equation (4.19) can be rewritten as

(4.22)

The above equation looks like the Ohm’s law of, where

. The quantity in of Equation (4.22) represents the field of force. It is a kind of force that promotes the growth of clusters such that the change in the Gibbs free energy G goes towards its minimum. It corresponds to the Chemical force of Ostwald and hence it was called the chemical resistance [121] .

Now, from this point of view the growth process of clusters

(4.23)

can be regarded as a system of resistances in series in an electrical circuit following the Ohm’s law. In the nucleation process the resistance at the size of nucleus is the largest, and indeed the rate J of the process is determined by it.

Motoyosi Sugita noted the following: The mathematical form of Equation (4.22) is much more convenient than that of Becker etc. It is not the equation to show the destiny of the growth and the decomposition of clusters. Each cluster emerges as a result of statistical and thermal fluctuations and the system moves towards its dynamic equilibrium by following the field of force as the needles of a clock move. This idea becomes very important when we think of crystal growth and life being. What is important here is not the quantitative treatment but the qualitative treatment of the theory. In order to introduce the concept of the field of chemical potential, i.e., the m-field, the expression of J was written in the form of Equation (4.22) in terms of the chemical potentials and the chemical resistance. Here has been assumed to be determined empirically by an experiment. Thus, the above theory of the Ohm’s law like theory is a phenomenological one or a rough preparation for the more exact and detailed theory that will appear in the future. When will be calculated mathematically using molecular statistics, one has to take into account fluctuations and improve the mathematical method of statistical mechanics. But at this stage we restricted ourselves within the phenomenological or rough preparation theory.

5. Thermodynamics of Transient Phenomena of Motoyosi Sugita

As is noticed in the above, the theoretical framework of the above theory is very general. Becker and Döring [96] as well as Volmer [97] applied it to the two-dimensional crystal growth on the surface of crystal. Indeed Motoyosi Sugita applied it to many physical systems in the broad quasi-static change or in the metastable state from physics to biology [4] [5] [6] [41] - [91] . In this section, I would like to focus our attention on the application to chemical reactions.

5.1. Motoyosi Sugita’s Theory of Chemical Reactions

Let us consider the chemical reaction of the following form [104] :

(5.1)

where () stand for the reacting (produced) molecules and () are positive integers representing stochiometry of the reaction. For example, a simple reaction case looks like the following:

(5.1’)

On the other hand, Motoyosi Sugita [3] [60] frequently used the following expression for it:

(5.2)

where () stand for the reacting (produced) molecules and () are positive integers representing stochiometry of the reaction. He distinguished the reacting or produced molecules by i or j.

Denote by () the number of reacting (produced) molecules of ith (jth)

species in mole (simply called the mole numbers). Let us denote by and the concentrations per mole of molecule and, where

. The changes in mole numbers of the reacting and produced molecules are represented by

(5.3)

where and are all positive integers. Here and are called the extent of

reaction or degree of achievement and the reaction rate by Theophile De Donder [102] [103] [104] , respectively.

On the other hand, Motoyosi Sugita used instead of and regarded it as the increment in molecular numbers such that

(5.4)

where i and j stand for the reacting and produced molecules. In this way Motoyosi Sugita emphasized the change of molecular numbers in molecular statistics [3] [5] [60] , while the De Donder’s school emphasized the change in the reaction equations [102] [103] [104] .

Following Motoyosi Sugita’s theory [5] , let us define the Gibbs free energy G as

(5.5)

where and are the number and the chemical potential of the molecule, respectively, and all indices for reacting (i) and produced (j) molecules have been included in the same index k. Equivalently, this induces to the following definition of the chemical potential:

(5.6)

It means that if the amount of of the kth molecules is added to the system from outside, then the work of

(5.7)

is done such that the Gibbs free energy increases. Since the sum in the Gibbs free energy G is linear in, it shows a homogeneous equation. Hence, we have

(5.8)

Using the reaction equation of Equation (5.4), we have

(5.9)

where if then the reaction moves from the left to the right. Substituting Equation (5.9) into Equation (5.8), we can derive the following:

(5.10)

where is defined by

(5.11)

This is nothing but the Affinity introduced by De Donder [102] and Progogine [103] [104] before WWII as well as Marcelin [122] and Jouguet [123] even before WWI in Western countries.

From the knowledge of thermodynamics, G becomes the minimum when the system goes to chemical equilibrium. Hence, in chemical equilibrium,; in other words. Therefore, if we regard as a variation, then we find

(5.12)

This yields the following criterion for the direction of the reaction of Equation (5.2):

(5.13)

This is the criterion given through the concept of affinity.

Let us denote by the mixing entropy [see Equation (3.23)] of the system of chemical molecules. The Gibbs free energy G can be written as

(5.14)

Simply suppose that the mixing entropy is approximately given as

(5.15)

where is the gas constant as before. Substituting Equation (5.15) into Equation (5.14), the chemical potential is given by

(5.16)

Substituting these into in Equation (5.11), we obtain

(5.17)

This yields

(5.18)

where we have defined as

(5.19)

Rewriting Equation (5.18), the law of mass action in the chemical equilibrium is given by

(5.20)

where is called the equilibrium constant at temperature T.

Now let us consider when the system is not in equilibrium. In this case, Equation (5.4) yields the rate equation:

(5.21)

where means the reaction coefficient for the forward (from the left to the right) process while means the reaction coefficient for the backward (from the right to the left) process. We now define the relationship between, and K as

(5.22)

Here if we may follow the argument of Prigogine et al. [103] [104] , then we may define as

(5.23)

where

(5.24)

5.2. Motoyosi Sugita’s Concept of the Generalized Nonlinear Ohm’s Law

Following the theory of Motoyosi Sugita [5] , let us define the chemical resistance to the chemical reaction by

(5.25)

Here I would like to note the following: If we rewrite as

(5.26)

respectively, then we can derive the relation of detailed balance:

(5.27)

Thus, the equation for (Equation (5.25)) indicates a kind of the detailed balance equation.

Motoyosi Sugita jumped over the standard way of thought and he assumed that the chemical potential is meaningful even when the system is not in equilibrium yet. Therefore, he assumed for all components of the molecules

(5.28)

Using Equation (5.28) together with Equation (5.25), he was able to rewrite Equation (5.24) as follows:

(5.29)

(5.30)

Applying these into Equation (5.21) or Equation (5.23) and rewriting, he

was able to derive the following:

(5.31)

This expression has the generalized nonlinear form of the Ohm’s law:

(5.32)

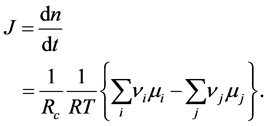
Now we are able to know the following relation:

(5.33)

where means that the left hand side is equivalent to the right hand side. Thus we can have the same criterion as that in Equation (5.13) by considering Equation (5.32):

(5.34)

5.3. Motoyosi Sugita’s Concept of the Field of Chemical Potential

Equation (5.31) was first introduced by Motoyosi Sugita long long time ago [23] [29] [60] . He was inspired by the expresson of Equation (4.22). It was derived by Becker and Döring [96] , Volmer [97] and Frenkel [98] (shortly represent BDVF). They studied the theory of condensation considering the nucleation of clusters in the supersaturated state. Therefore, it describes the non-equilibrium state in the irreversible process of condensation.

Motoyosi Sugita recognized that when chemical equilibrium is slightly broken or when chemical reactions are going on, the physical conditions in chemical reactions are the same as those in condensation as well as nucleation. Thus I would like to express schematically the relationship between the Sugita’s J and the BDVF's J in the following:

(5.35)

The mathematical form in in the above represents a kind of chemical force. This concept is different from another concept of chemical force, Affinity of De Donder [102] [103] [104] . The affinity is defined as in Equation (5.11). On the other hand, the Sugita’s concept of a kind of chemical force is related to the change in molecular numbers in Equation (5.10). Motoyosi Sugita called it the m-field or the filed of chemical potential [3] . Both types of chemical forces acting on either or () take place in the irreversible processes. Thus, he emphasized the use of the concept of the filed of chemical potential to most of all transient phenomena.

As was discussed before in the previous section, in Equation (5.35) one can derive the above expression for J without any problem. However, the expression for cannot be derived from the theoretical framework of equilibrium statistical mechanics. It is a phenomenological expression that is supposed to be determined in experiment. Never- thless, later some kind of its justification was performed by Eyring et al. [124] [125] using the statistical method. And Becker and Döring [96] and Volmer [97] required the kinematical treatment in the theory. Therefore, Motoyosi Sugita called in this situation kinematical situation. On the other hand, he stated that when one went deep into the details, one became stuck without stepping forward any further since one met very difficult problems lying down in statistical mechanics. In order to escape these difficulties, one has to be satisfied with only considering the so-called the quasi- thermodynamics. It is slightly generalized to adjust with the transient phenomena, using the concept of m-field. By this approach, one becomes able to apply the idea and concept to many biological systems. He called this situation the equilibrium theoretical situation.

As an example, let us apply the concept to the condensation on the surface (of either liquid or solid). Denote by J the number of molecules per second that collide with the surface. Denote by the chemical potential for the phase I and that for the phase II. This is given by

(5.36)

Here () means the pressure of the phase I (II), where ().is the temperature of the system. M means the molecular weight of a molecule. is the total area of the surface. And stands for the permeability coefficient, which means that molecules colliding with the surface of phase II can be easily absorbed in the phase. Therefore, if then both phases are in equilibrium, if then the phase I goes to the phase II, and if then the phase II goes to the phase I.

Motoyosi Sugita recognized that this kind of rule for phase change seems very similar to that of the Gibbs’ phase rule for the equilibrium state [126] . In the former phase change occurs as a consequence of the broad quasi-static change in the irreversible process of transient phenomena, while in the latter phase change occurs as a con- sequence of the realization of equilibrium state. Thus there is a conceptual difference between them such as the former is time-dependent and the latter is not time- dependent. However, Motoyosi Sugita postulated the validity of the application of the concept of the field of chemical potential to many biological nonuniform systems such as polymers or macromolecules in protoplasm in cells.

Denote by K a part in a nonuniform system and denote by its chemical potential for component i in K and so forth. If there are three parts K, and in the biological nonuniform system, then we can assign chemical potentials, , and, respectively. Now if the system is in the equilibrium, then the chemical potentials satisfy the following condition:

(5.37)

and if the chemical reaction in equilibrium in the part K is given by

(5.38)

then the condition

(5.39)

must be satisfied. On the other hand, if the equilibrium is not yet attained, then the kinetic rate equation like Equation (5.35) and Equation (5.36) should be applied to describe the system. Even for dynamic systems such as the system of life or life being, if the system is in dynamic equilibrium such as fluid equilibrium or chemical equilibrium, then we may assume that Equation (5.39) is approximately satisfied in the sense of broad quasi-static change and of local equilibrium. This is the concept of the field of chemical potential introduced by Motoyosi Sugita long ago.

Now, let us turn back to the reason how Motoyosi Sugita noticed the concept of field of chemical potential, for a while. As mentioned in the previous sections, he studied the the quasi-static change in classical thermodynamics in Japan before WWII, where Japan was very isolated from Western countries occasionally dashing to the war. He found the way of exceeding it and called it the broad quasi-static change in quasi- thermodynamics. He understood that chemical potential has to be defined locally as a function of a field of the coordinates of the system such as. Otherwise he was not able to derive the Kelvin’s relation for the thermoelectric effect.

In my opinion, it is obvious that his way of thought came from this experience in his physics study, and then he applied the concept to other physical and chemical examples such as chemical reactions. The first look of Motoyosi Sugita for this discovery seems to be the following simple equation:

(5.40)

where means the electric potential acting on the molecule of species i and others are the same as before. Then he extended his way of thinking so that even if no electric potential exist, then the chemical potential as a field is meaningful. Onsager [100] [101] , Debye-Hückel [127] and Onsager-Samaras [128] used the similar ideas before. Why not for other systems? What’s wrong with this?

So, Motoyosi Sugita stepped forward to go beyond the equilibrium thermodynamics to the quasi thermodynamics of transient phenomena. Thus, although we think of chemical potential such as a numerical value for the equilibrium state in the standard point of view of thermodynamics, Motoyosi Sugita never thought like this but he always thought that chemical potential is a field defined on space-time such as the field in field theory even for dynamic, nonuniform, irreversible, non-reproducible and transient phenomena. This is his philosophy on the field of chemical potential.

5.4. Relationship between Cooperative Phenomena and Chemical Potential

Motoyosi Sugita further mentioned that the chemical potential plays an important role when the system undergoes phase change. It is not well-known in the recent modern text books in thermodynamics [103] [104] [105] [106] [108] [116] . This is the cooperative effect when the system undergoes a phase change in the irreversible process in transient phenomena. In other words, it can be dubbed the much more modern word, induction-association principle for the phenomena. The word inducetion- association principle was first introduced by Gilbert N. Ling [129] [130] and has been advocated by Gerald H. Pollack [131] [132] for a long time.

This very particular aspect of the phenomena is the following: When the system faces a phase change, if it undergoes the phase change, then it cannot occur so literally, however. Rather, it never occurs even when the temperature of the system already goes below the critical temperature at which the phase change is supposed to occur. This is the supersaturation phenomena, discussed before. At this moment, in order to make the system undergo the phase change, a nucleus or a stimulus, i.e., a kind of trigger is needed for the phase change. Otherwise, it stays still. Conversely speaking, even if the stimulus of a trigger is very very small or microscopically small, the entire system undergoes the phase change. Hence, the effect is very cooperative. This phenomenon is not perfectly understood yet even nowadays.

In order to understand this type of phenomenon, Motoyosi Sugita emphasized the importance of the concept of the field of chemical potential, namely the m-field. According to Frenkel [98] , even in solid, partially melt parts are included near melting point. But the parts do not develop so easily even below the melting point. He put it the name pre-melting. Motoyosi Sugita postulated that in such a case the m-field plays an important role. He imagined that the m-field is always fluctuating thermally or locally under various conditions. One good example is the cluster growth in the previous section. Local raise of the value of m-field promotes the local phase change in the system until the system goes to equilibrium. A local variation of m-field initiates the action at a distance to another point in the system. It is long-range interaction. Thus, local variation of m-field acts as a trigger for the phase change through the long-range interaction of m-field. This is the nucleation in the supersaturated phases.

In this way, the system can communicate through the m-field in the system just like when the electrical potential does. This means that m-field extends the lines of force as an induction of the generalized potential, the m-field. Mathematically, it may be con- sidered as the gradient of the m-field. Therefore, the idea of induction-association principle of Gilbert N. Ling seems very similar to that of cooperativeness of m-field of Motoyosi Siguta.

The cause of such lines of force comes from the m-field. The m-field consists of the mixing entropy term. Hence, the lines of force or the long-range interaction between the parts in the system appears as the consequence of the mixing entropy, e.g., the last term in Equation (5.40). In the standard viewpoint this nature of long-range interaction emerges as a consequence of electric effect. However, Motoyosi Sugita extended the concept such that so is true for the m-field as well. On the other hand, the action of energy is not long-range but local or short-range. Thus, the induction-action principle of Gilbert N. Ling and the cooperative effect of Motoyosi Sugita comes from the mixing entropy, not from the energy of the system.

Can one think of the field in life being as the m-field? He sometimes asked such a question. In such biomaterial or life or life being, the m-field is not made of a single component but is constructed by a huge number of components. Obviously, the structure of the m-field becomes very complex. If so, then it would be very very difficult to calculate the entropy term, calculating the partition number such as in Equation (3.23), since no simple formula exist for such complicated molecular systems. However, in principle and ideally, we can think of the Gibbs free energy G, the number of partition W and the sum of states Z, etc. Then we can expect that the system can move towards the direction of and the motive force for it is related to the m-field from the point of view of quasi-thermodynamics.

His conclusion is as follows: The m-field is very long-range enough to affect each other. A slight variation such as temperature fluctuation can be eliminated by the cooperativeness of the entire system. Therefore, when one has to apply thermo- dynamics to the system in considering the entire system as a whole. Especially the second law of thermodynamics is such a law. One must be very careful when he applies the second law of thermodynamics to the partial systems. It is sometimes said the following: Since life is not a closed system, we cannot apply the second law of thermodynamics to life. This seems a ridiculous idea, since it misses the point. While one takes into account the Gibbs free energy, one may consider the partial systems, under the condition that temperatue is constant, one may consider the other parts as thermal sources by which some parts can be affected with other parts through the thermal communication to each other.

5.5. The m-Field, as an Invisible Force

In the previous example of the cluster growth in the supersaturated phase, the clusters grow like this:

(5.41)

Here in between the nearest states of clusters and Equation (4.22) holds

(5.42)

The field of chemical potential of in the above expression acts as an invisible force and statistically dominates this cluster growth. It has a tendency of action that the mixing entropy is increased as large as possible and the Gibbs free energy is decreased as small as possible. This tendency appears to be the hidden invisible force to make clusters grow. As seen in Equation (5.41), the is acting in series, which corresponds to the current between the nodes in electrical circuit. On the other hand, chemical resistance is in series as well, where chemical resistance corresponds to resistance in electrical circuit. The current J is stuck to be very small right before the nucleation size, being disturbed by the very large chemical resistance. Therefore, the cluster with maximum size (n) near the critical size of nucleus has its maximum resistance and hence the rate (although). The system wants to go to the nucleus but cannot exceed; this means quasi-stability. This nearly equilibrium state in the supersaturated phase right before the phase change is sometimes called false equilibrium.

In Equation (4.8) as n becomes large, becomes negatively large such that the entropy becomes locally small. The reason why such a state appears is that if such singular parts (i.e., large clusters) are included in the system, it becomes more convenient to make the total G small. Such an action that makes entropy small is also due to the invisible force, the m-field. Apparently the second law of thermodynamics seems to be broken, but it is not so. Once we see the entire system, the second law of thermodynamics has never been broken.

After the growth processes of non-equilibrium thermodynamics are finished, once such clusters or complicated life being develop their structures, the fully developed structures of such clusters or fully developed complicated structures of life being consist of very large Gibbs free energy by definition. This complicated situation seems to contradict the laws of thermodynamics.

Thus, Motoyosi Sugita noticed that there might exist some kind of hidden law of thermodynamics in addition to the three laws of thermodynamics. He postulated that there might exist the 4th law of thermodynamics which dominates the speed of the transient phenomena as mentioned in the introduction.

6. Motoyosi Sugita’s Concept of the Maximum Principle in Transient Phenomena

In this section, let us consider the most important contribution of Motoyosi Sugita in my viewpoint. As discussed in the previous section, the concept of the filed of chemical potential is quite important when we considerate the non-equilibrium processes.

6.1. Motoyosi Sugita's = Max Conjecture and the 4th Law of Thermodynamics

As early as in 1950 Motoyosi Sugita wrote a paper entitled in Japanese, Biological Thermodynamics and its Method, which was published one year later from the Annals of the Hitotsubashi University, entitled in English Thermodynamical Method in Biology [60] . He stated in Japanese on the existence of the 4th law of thermodynamics [29] as the paragraph quoted in Introduction. And also he first applied his theory of thermodynamics in the transient phenomena to the theory of metabolism.

For the reason why Motoyosi Sugita believed the existence of the 4th law of thermodynamics, he listed several examples that seem to be related to this 4th law as follows:

Here let us see many instances suggesting this large principle of thermodynamics.

1) The cascade principle(Stufenregel) found by W. Ostwald [97] shows that the nature has the tendencies as if it wanted to take the pass of smaller resistance or make a de tour and want to establish the equilibrium as fast as possible.

2) Generalizing further the rule described above, it might be said that the nature prefers the line of the least resistance, if there are ways side by side for the equilibrium.

a) According to Volmer [97] , for instance, the crystal formation shows that such a pass is taken actually.

b) Eyring and others [124] [125] called such a process rate determining.

c) Electric current in conductor takes the distribution that heat loss is minimum if the total current takes a given value. Therefore the heat generation must be maximum if the potential difference will be taken as constant. Therefore, if a cell is applied to drive the current, it will take the distribution to dissipate the free energy of the cell as fast as possible.

d) Onsager [100] [101] has derived his reciprocal relation from the principle of least dissipation function. This principle might be considered to the maximum velocity of entropy increase which will be discussed later.

3) If a new passage is built independently which has less resistance than others already existing, then the circumstance above described, that might be the 4th law of thermodynamics, may also be seen from our common sense.

a) The new way may be considered having delicate catalytic action, therefore, large free energy of activation or small entropy. The free energy of activation determines the rate of development of such a passage acting as if the initial cost is to construct a highway. That is why the construction of the way of small resistance is retarded. Nevertheless, it becomes rate determining when it is performed and the old ways become only bypass or will be ruined.

b) The idea of natural selection or struggle for life of biology may be considered as having the relation to this principle. That is the free energy discharged through the old passage is used to the free energy of activation of new way, and the material itself constituting the old way may be useful also as the material of construction (see (v) of VI).

c) Such a circumstance like natural selection can be seen also in the inorganic worlds. For instance, let us observe the nuclear formation of ice in supersaturated water vapor under freezing point, and containing super-cooled water droplets. If the crystal nucleus is formed, not only the condensation occurs on this nucleus, but the super-cooled droplets vaporize and disappear. This is the consequence of the 4th law and the same phenomena can be seen on the discharged plate of PbSO₄ of battery and also in the case of recrystallization of metals and others, and they are playing a role to promote the tendency to the thermodynamic equilibrium.

Thus from the early beginning of his research he recognized and imagined the existence of the 4th law of thermodynamics, where he expected that some kind of the generalization of the least dissipation of energy of Onsager could be necessary. Therefore, I would like to call his expectation the Motoyosi Sugita’s = max conjecture.

In the next section of that paper [29] [60] , VI. Mathematical Theory and Conclusion, he sketched the outline of the 4th law of thermodynamics as follows:

1) First, on the base of microscopic reversibility, Onsager [100] [101] has shown that. Exactly speaking, it is given by

(6.1)

where is the velocity of entropy increase of the total system and is the dissipation function in the sense of Rayleigh [133] as usual or such.

2) On the same base as Onsager, Landau and Lifshitz have shown that

(6.2)

in their statistical physics [134] .

3) Let us denote by the parameter expressing the transient state, and let us assume that G is expressed by using the cut off method, then

(6.3)

(6.4)

where is the chemical potential of the kth component, is its constant part, is its concentration and is the reaction velocity.

4) Let us consider quasi-chemical processes

(6.5)

between the components. This describes a set of chemical reactions such as chain reaction, whose set is denoted by s. It means that there are many chemical reactions that consist of a finite number set of molecules and labelled by i and j.

5) Let us denote by the reaction velocity of the process s from the left to the right. The reaction velocity can be written in the form:

(6.6)

Through this linear transformation, the variables can be transformed to. The number of new parameters may be less than and they may be inde- pendent variable.

6) Substituting Equation (6.6) into Equation (6.3), we find

(6.7)

where we have defined the affinity of the reaction s as

(6.8)

I would like to note here that there is a sign mistake for Equation (6.79) in the English version of this paper [60] .

7) From the rate theory of chemical reaction, can usually be written in the form:

(6.9)

where is the chemical resistance of the process s, which corresponds with the circumstance of the theory of rate process, and the quantity in the bracket represents the m-field, that corresponds with the circumstance of the theory of equilibrium.

8) Inserting Equation (6.9) into Equation (6.7), we can see that is equal to, where H is the Boltzmann’s H-function. If the mean value of H is taken in the momentum space and if it is assumed that s represents only the rate determining precesses in the individual processes and that the higher term of is negligible, then we obtain

(6.10)

The procedure, which neglected the higher term, corresponds with the cut off method discussed in Section 2. The summation of the right hand side of Equation (6.10) may be interpreted as, where is the dissipation function of the quasi- chemical processes, and it may be considered as the virtual heat source discussed in Section 2.

9) The reversal of the m-field can be interpreted if we consider the transition from the stage

(6.11)

In the above paper [29] [60] Motoyosi Sugita was not able to present the detail of the proof of the conjecture. It was limited to suggest the existence. However, in the succeeding papers [40] - [46] [48] [61] [75] [77] [78] [79] he argued the sketch of the conjecture and frequently tried to prove it.

6.2. Relationship between the Boltzmann’s H-Function and the m-Field

In order to investigate the Motoyosi Sugita’s conjecture, the so-called Boltzmann’s H-function plays an important role. So, let us first consider the relationship between the Boltzmann’s H-function and the m-Field for the molecular statistics. For this purpose I would like to restrict ourselves to consider the system of chemical reactions only. However, this way of thinking can be generalized to other physical, chemical and biological systems as well.

Since there is a basic idea for proving the conjecture in [75] , I would like to follow it here. Motoyosi Sugita first defines the Boltzmann’s H-function for chemical reactions by

(6.12)

where are defined by Equation (6.4) and stand for its chemical equilibrium values. The above form of the H-function is justified as long as one adopts the formula for the partition function W such as Equation (3.23) by the cut-off method of Motoyosi Sugita. It obviously satisfies the following:

(6.13)

And if we write then

(6.14)

where the equality holds true only when. This means that the H-function in the equilibrium state is always minimum.

Next, let us consider the derivative of H-function with respect to time along the course of time development. Then, Motoyosi Sugita considers the following:

(6.15)

Let us consider the chemical reaction equations such as Equation (5.21) for chemical reactions of Equation (6.5), for our case here. Associated with the choice of the reaction Equation (6.6), we can write the chemical reaction equations in the following:

(6.16)

where P and R mean production and reduction in the chemical reactions, respectively, and is defined by

(6.17)

where, and are defined by

(6.18)

and

(6.19)

respectively. On the other hand the affinity for each chemical reaction is defined by Equation (6.8). The chemical equilibrium values are obtained by

(6.20)

Obviously this produces the law of mass action such as Equation (5.22) for each chemical reaction:

(6.21)

Substituting all into Equation (6.15) using the definition of chemical potentials Equation (6.4), finally Motoyosi Sugita ends up with

(6.22)

This is nothing but Equation (6.10), where can be regarded as the virtual heats in the transient chemical reactions. Motoyosi Sugita shows that this satisfies the following theorem:

Theorem 1 (Boltzmann’s H-theorem).

(6.23)

Let us now prove the H-theorem. Following the similar argument of Motoyosi Sugita [75] , we find the following:

(6.24)

where is given by Equation (6.17). Now if we denote as

(6.25)

then the summand looks like

(6.26)

Since, the last expression is identically less than or equal to 0.

The equality holds only for the equilibrium. Hence, the theorem is proved.

6.3. Motoyosi Sugita’s Idea for the Proof of the Conjecture

Motoyosi Sugita also considered more general case of the nonlinear processes, which may be represented by the following equations:

(6.27)

where x means a vector of and stands for any function of x. The stationary state of these equations are assumed to be given by

(6.28)

The stability of this system is investigated by the Lyapunov theorem. Denote by. Let us discuss the stability around the stationary state. The equation of motion for y is given by

(6.29)

where we have assumed that can be represented in terms of y_i such that.

Now the simplest Liapunov function is defined as

(6.30)

By differentiating this with respect to t, we obtain

(6.31)

If all real parts of the eigenvalues of the Jacobian matrix are negative, then the stationary state becomes asymptotically stable. This is a satisfactory condition for the theorem. Here if J_ij = J_ji, then the theorem is always true.

Motoyosi Sugita applied this theorem to the Boltzmann’s H-function. And he proved the H-theorem is valid if the Lyapunov’s theorem holds.

Let us define the general Boltzmann’s H-function:

(6.32)

By differentiating the above equation, we immediately obtain

(6.33)

Motoyosi Sugita proved a mathematical theorem:

Theorem 2. If can be Taylor expanded around the stationary state, then it can be rewritten as

(6.34)

where are the parameter integrals defined by

(6.35)

Let us follow his proof, which is short. By assumption, we expand around the stationary state in Taylor series. We obtain

(6.36)

Let us define and as

(6.37)

(6.38)

Using Equation (6.37), the Jacobian can be Taylor expanded in the following:

(6.39)

The remained procedure is to use Equation (6.35) and Equation (6.39) and to derive the right hand of Equation (6.34).

(6.40)

Hence, the theorem is proved. This is nothing more than the mean value theorem in the analysis for the analytic functions with many variables.

Using this theorem, Equation (6.33) turns out to be the following:

(6.41)

Now if all the real parts of are negative, then since and

have the same sign. Therefore, we can obtain the following:

(6.42)

By differentiating Equation (6.33) with respect to t, we obtain

(6.43)

The second term in the above is always positive. Let us now substitute Equation (6.29) into the first term, we find

(6.44)

By definition. And in our assumption that is diagonalizable and

the Liapunov theorem is valid, all the real parts of eigenvalues of the Jacobian are negative. Hence, by multiplication, Equation (6.44) is always positive. From this fact, we obtain the following property of the H-function:

Theorem 3.

(6.45)

Let us define the entropy production of the system by

(6.46)

where k is the Boltzmann constant. Therefore, from Theorem 3 we immediately yield the following theorem:

Theorem 4.

(6.47)

This is nothing but the theorem of the minimum entropy production or the Prigogine’s principle of minimum entropy production [103] [104] .

In summary, this is the outline for the proof of the conjecture proposed by Motoyosi Sugita [75] . He tried again and again to prove this conjecture from various point of view. However, the general proof has never been done in his life time.

7. The Ideas of Motoyosi Sugita as a Specific Development of Lars Onsager’s Lifework

In 1951 Motoyosi Sugita first presented the theory of the maximum principle in transient phenomena such as those discussed in the previous section [38] . This paper was entitled as The Maximum Principle in the Transient Phenomena and the Application to Biology in Japanese. In this paper he first stated his vision and idea on the maximum principle in the transient phenomena. He argued the relationship between his idea of maximum principle and the existing old ideas such as the maximum-minimum principle in the Joule heat, the Boltzmann’s principle in the theory of gases, and the Onsager’s principle of the least dissipation of energy in the theory of irreversible processes [100] [101] . He finally applied his idea to many biological systems such as the thermodynamics of metabolism, the relationship between the maximum principle and the metabolism, the origins of life, and the dynamic equilibrium, the relaxation oscillations, the wholeness of life, etc.

In the succeeding paper in 1952, he further studied the maximum principle in relation to the Boltzmann’s H-theorem [40] . This paper was entitle as The Relationship between the Boltzmann’s H-Theorem and the Dissipation Function in Japanese. This paper is a really instructive one. As is discussed in the previous section, his theory preceded the times of Prigogine [103] [104] . So, in this section I would like to present his comparison between the Motoyosi Sugita’s theory and the Prigogine’s theory as well as Onsager’s theory [100] [101] and Katchalsky’s theory [105] [106] [108] . Fortunately for the Western people, these Japanese papers were summarized as the English versions [77] - [79] .

7.1. Relationship between the Boltzmann’s H-Function and the Irreversible Work

As is shown in the previous section, we have obtained the Boltzmann’s H-function, especially for the case of chemical reactions. Motoyosi Sugita first applied his idea of the virtual heat that has been discussed in the section II to the irreversible work of the system.

In order to see the difference between the method of Motoyosi Sugita and that of Ilya Prigogine more easily, let us change the notation of Motoyosi Sugita to adjust with that of Prigogine. Let us denote by i the internal system which is doing the irreversible work. Let us denote by e the external thermal reservoir, where we assume that no irreversible work has been done. By definition, we have

(7.1)

If the process is the broad quasi-static change (under the isothermal and isopressure), then we have

(7.2)

which is equivalent to

(7.3)

This is not satisfied when the irreversible work exists. In this case we have

(7.4)

which is the isothermal irreversible work. Or equivalently,

(7.5)

On the other hand, since the heat comes out from the reservoir e, we have for the reservoir e

(7.6)

Now we assume that there is no heat exchange otherwise, the total entropy of the system is given by

(7.7)

Since there is no irreversible work in the reservoir e,. And since G is always decreasing, we can state that. This is the irreversible work for the entire system and it is nothing more than "virtual heat" introduced by Motoyosi Sugita long ago. Then we have

(7.8)

This suggests that there exists the maximum principle in the transient phenomena in terms of the Boltzmann’s H-function. Hence, his conjecture is crucially important in the theory of non-equilibrium thermodynamics in the irreversible processes in the transient phenomena such as life. It also suggests the existence of the 4th law of thermodynamics.

On the other hand, Prigogine only showed that for the internal system

(7.9)

This means that the entropy of the internal system is always increasing. There is no explicit expression like Equation (7.5) in the theory of Prigogine based on and tracing the origin back to the school of De Donder [102] [103] [104] . As was discussed in the section II, the above Prigogine’s equation leads to a confusion and a mistake when one considers the irreversible cyclic processes. Because in the viewpoint of De Donder’s school the entropy of the cycle can vanish only when the cycle is reversible; otherwise it must be positive such that

(7.10)

However, as Motoyosi Sugita discussed long long ago, no matter what the irreversible process is taken into account, the following must be satisfied when the internal process is cyclic since the final state must come back to the initial state after one cycle:

(7.11)

On the other hand, as is shown in Section 2 [see Equation (2.19) and Equation (2.23)], we must have for the external reservoir after one cycle

(7.12)

This is the advantage of the Motoyosi Sugita’s concept of the virtual heat for the irreversible processes in the transient phenomena.

7.2. Relationship between the Boltzmann’s H-Function and the Dissipation Function

This argument can be generalized to the systems of flow dynamics or fluid dynamics. In this case there is matter exchange between the reservoir e and the system i. Let us denote by the external part of G and by the internal part of G, respectively. In the stationary state of the internal system i, the time derivative of vanishes (i.e.,). So, we have

(7.13)

This must have the same form as, which becomes the dissipation function of the system; that is. Hence, we must have

(7.14)

or equivalently

(7.15)

This simple looking but very important relation was independently rediscovered by Katchalsky much later [105] [106] [108] . What is important here is that the above equation is valid even for open systems such as the flow or fluid dynamics as well as life systems.

Now Motoyosi Sugita imposes the maximum principle for this relation as follows: Suppose that (or) represents the dissipation processes in the transient phenomena. For example, let us consider the metabolic system. Then, (or) represents the reduction processes in the metabolic system. Then denote by M the amount of creation per second, while denote by the dissipation per second. Let us define. Then, we seek the extremum such that becomes the

maximum under the restriction that. This is the content of Motoyosi Sugita’s variation principle of the maximum in the transient phenomena [40] . Thus, I would like to summarize the Motoyosi Sugita’s maximum principle as follows:

Theorem 5 (Motoyosi Sugita’s Maxmum Principle) Under the constraint, find the maximum of the following equation:

(7.16)

Thus Motoyosi Sugita challenged us who can prove this principle in general. Whoever can do so, then the 4th law of thermodynamics is proven.

7.3. Relationship between Motoyosi Sugita’s Theory and Lars Onsager’s Theory

Following the idea of Lars Onsager [100] [101] [118] [119] , the entropy change can be divided into two parts such as

(7.17)

where means the entropy change inside the system and means the entropy change due to the interaction between the system and the environment.

Let us define the state variables,. And the changes in entropy are supposed to be represented in terms of x's. If one can expand the stationary entropy around the equilibrium entropy inside the system with respect to x’s, then we must have

(7.18)

where stands for the entropy production in the system at time t and t means an infinitesimal time. If the process that we are considering is an irreversible process of the states’s, then the total derivative in time of provides

(7.19)

Equation (7.19) together with Equation (7.18) yields

(7.20)

where

(7.21)

Here are called the generalized flows, while are called the generalized forces.

Considering Equation (7.20) together with Equation (7.19), Onsager postulates the following variation principle:

(7.22)

Or equivalently,

(7.22')

Here Onsager assumes that the quadratic dissipation function is given by

(7.23)

where is called the Rayleigh’s dissipation function.

By the variation principle for Equation (7.22) or Equation (7.22'), we have to consider the following variational equation:

(7.24)

From this, we obtain

(7.25)

Substituting Equation (7.23) into Equation (7.25), we obtain the famous linear relation:

(7.26)

where the coefficients satisfy

(7.27)

This is the Onsager’s reciprocal theorem. Solving Equation (7.26) for, we obtain

(7.28)

where; the reciprocity holds true for. This yields for the dissipation function:

(7.29)

The variational principle of the above equation is given as

(7.30)

Apart from the energy dissipation through the surface, we finally obtain

(7.31)

Since for the isothermal system the internal energy is kept constant, the rate of the Gibbs free energy is related to the entropy change such that. Hence, we obtain

(7.32)

as expected, where is the Rayleigh’s dissipation function.

Now I would like to note that the variational principle of either Equation (7.24) or Equation (7.30) falls into the Motoyosi Sugita’s maximum principle discussed before [see Equation (7.16)]. In the above case of Onsager’s minimum or maximum principle, Onsager implicitly assumed that there exists a constant M such that. Instead of showing that, Onsager also implicitly assumed that for the variation of Equation (7.24) and for the variation of Equation (7.30), respectively. Since the constraint either or is assumed, the extremum of either or after the variation is also constant. Hence, is constant as well. Thus, Onsager’s principle of the least dissipation of energy falls into the Motoyosi Sugita’s maximum principle as a special case.

Next let us consider the relationship between the Motoyosi Sugita’s m-field and the the above Onsager’s theory. As is shown in the above Onsager’s relation between the generalized forces and the generalized flows(or currents) are linear [see Equation (7.26) and Equation (7.28)]. However, in the Motoyosi Sugita’s theory it is not so but it is nonlinear. Going back to Equation (6.10), we hold the following relation:

(7.33)

where from Equation (5.31) or Equation (6.17), is given by

(7.34)

Let us suppose that the system is nearly in the thermodynamic equilibrium as was considered by Onsager. If we assume

(7.35)

where is the enthalpy and the concentration (or activity) of the component i, then

(7.36)

where and are the reaction constants for the forward and backward processes given by

(7.37)

respectively. Then,

(7.38)

Or inversely,

(7.38')

Formally solving the above for, we obtain

(7.39)

where are the expansion constants. On the other hand, following the expansion,

(7.40)

might be obtained if is the equilibrium value and is the constant. Now Equation (7.33) can be rewritten in the following form:

(7.41)

which can be written in the quadratic form like Equation (7.23) if the terms of the higher order of are neglected and is transformed into by

(7.42)

where are constants. Then the reciprocal relation of the coefficient of is easily derived. Thus, Onsager’s functional and the linearity can be derived from the Motoyosi Sugita’s m-field theory as a special limit [77] [78] [79] .

7.4. Relationship between Motoyosi Sugita’s Theory and Ilya Prigogine’s Theory

Following the idea of Prigogine [102] [103] [104] , Prigogine assumes that the entropy increase of the system is given by

(7.43)

where Prigogine’s and are the affinity and the degree of the rate of the process of De Donder [102] and they correspond to the Motoyosi Sugita’s and, respectively. Generalizing this idea to more general chemical reactions, Prigogine [104] formulated almost the same method as that Motoyosi Sugita did long ago. Prigogine wrote as

(7.44)

while the affinity can be rewritten by

(7.45)

where is the gas constant as before and T the temperature of the system. Substituting Equation (7.44) and Equation (7.45) into Equation (7.43), we obtain

(7.46)

This looks different but it is equivalent to Equation (7.33). The correspondence between the Motoyosi Sugita’s theory and the Ilya Prigogine’s theory is as follows:

Sugita (1951) [38] Prigogine (1999) [104]

(7.47)

Thus I can conclude that Motoyosi Sugita succeeded in formulating the theory of non equilibrium thermodynamics long before it was reformulated again and intensively applied by the Prigogine’s school. Unfortunately, since such papers were written first in Japanese and published in Japanese journals such as the Bulletin of Kobayasi Institute and the Journals of the Hitotsubashi University, the contents of his theory have never been appreciated worldwide. This was really unfortunate for us to study his theories. This is one of the reasons why I am writing this paper.

8. The Relationship between the Motoyosi Sugita’s Maximum Principle and the Pontryagin’s Maximum Principle

Now I would like to prove the conjecture of Motoyosi Sugita’s Maximum Principle, using the optimal control theory [135] - [141] . From this, the relationship between the Motoyosi Sugita’s maximum principle and the Pontryagin’s maximum principle becomes clear. I would be able to conclude that the Motoyosi Sugita’s Maximum Principle is nothing but the Pontryagin’s maximum principle in the theory of optimal control.

As I have written in the introduction, I became aware of Motoyosi Sugita’s work in this Spring in 2016. Two years before this year, I have written a couple of papers on the application of the optimal control theory to thermodynamics [142] [143] . Therefore, at that time I did not know the research work of Motoyosi Sugita at all. However, once I became familiar with his work on the maximum principle that is given in Equation (7.16), I became sure that his maximum principle is nothing more than that of Pontryagin [135] [136] such that I can prove it using the theory of optimal control. This approach will be a generalization of the Motoyosi Sugita’s proof given in Section 6. And it will fill in the lack of proof for the conjecture of Motoyosi Sugita with a rigorous one.

Before doing so, I would like to present my philosophy for the problem, since my motivation has come from the very different viewpoint from that of Motoyosi Sugita. I would like to show it in the next subsection first.

8.1. Attractiveness of the Formulation of Classical Mechanics

What is most attractive in the theoretical framework of classical mechanics is as follows:

We believe that the energy is conserved in any mechanical problem, unless there is no dissipation of energy. This is the concept of energy conservation law. Based upon this energy conservation law, we assume that the initial energy is given in the problem for the mechanical system such as a pendulum or a spring. So, as long as there is no dissipation of energy, once the initial energy is given to the system, then it moves automatically and forever. This is our understanding on the physics of macroscopic mechanical objects.

As we know in classical mechanics, all variables in the system are mechanical variables such as the coordinates whose vector is given as and its momenta whose vector is given as. The set of the vectors forms so-called the phase space for the Hamilton dynamics which is given by the Hamilton equations of motion.

On the other hand, in our problem of non-equilibrium thermodynamics for the systems of life or living things, the system is described by dynamical change of the densities of ions, atoms, molecules, etc. under chemical reactions. So, the densities are given as a sum of the sets of classical particles or objects. At a given time the system is determined by the instantaneous values of the densities in the system. Since the system is dominated by the densities, we may call them the state variables. Thus, we have to treat the macroscopic state variables as the new type of mechanical variables in the dynamical systems.

This means that we regard the biologically living macroscopic system as a classical mechanical system given by regarding the state variables as the mechanical variables. This point of view is interesting, since we can regard the living objects as classical mechanical objects. As if a pendulum moved automatically following the energy conservation law, the macroscopic biological system would move automatically following some unknown law of physics. If such a new type of law exists, it will be very nice. I would like to find such new principle of conservation law. This is our goal here.

8.2. Modern Control Theory and Pontryagin’s Maximum Principle

The above vision of mine seems quite similar to that of Motoyosi Sugita. What I stated as the unknown law of physics is absolutely what Motoyosi Sugita stated as the 4th law of thermodynamics long ago. Since there are many detailed mathematical proofs for the Pontryagin's maximum principle, I would like to skip such proofs in this paper, but only show the essence of the proof. If you want to see such proofs, then I would like to recommend you to consult other books [135] - [141] and my papers [142] [143] .

In this section, we are going to consider the essential concepts and the formalism of the so-called Pontryagin’s theory of optimal control [135] [136] for the later purposes. This theory is the totally new type of extensions of the standard control theory [144] which is based upon the negative feedback mechanisms before 1960. Since then, the Pontryagin’s theory was called the modern control theory, while the old control theory was called the classical control theory. This reminds us of what happened in the discovery of quantum mechanics.

On the other hand, theoretically speaking, the Pontryagin’s theory of optimal control is the natural extension of the formalisms of Hamilton’s principle and the least action principle in classical mechanics [134] . It was totally a revolution in theoretical physics as well. However, much has long been not so well-known in physics society. It seems because the revolution has occurred in the optimal control theory and the automatic control theory in engineering community around the year of 1960 and because the value of scientists of USSR was intentionally and absolutely ignored by the Western scientists at that time in the era of the cold war between USSR and USA. This was very unfortunate.

8.3. Equations of Motion for the Open Dynamical System

Let us denote by the n-dimensional state vector for the state variables. Let us denote by the r-dimensional control vector for the control variables. The equation of motion for the dynamical system is given by

(8.1)

namely,

(8.2)

As in the case of classical mechanics, once we regard the state variables x as the classical variables, we can define a Hamiltonian. Let us denote by the adjoint vector for the adjoint variables. Let us define the Hamiltonian:

(8.3)

According to the Pontryagin’s theory of the optimal control [135] [136] , we can prove the Hamilton equation:

(8.4)

(8.5)

In order to escape from the confusion between the standard Hamiltonian in classical mechanics due to Hamilton and the Pontryagin’s Hamiltonian in the optimal control theory, we would like to use the Pontryaginian or Pontryagin’s Hamiltonian for the latter. This is because they are totally different from each other in a physical unit. Hamiltonian is given in units of energy [Joules], while Pontryaginian is given in units

of work rate, [Joules/sec], or power, , [Watts].

Equation (8.4) provides nothing but the original equations of Equation (8.1) by definition. Equation (8.5) is something else. But it can be regarded as a generalization of the speed of change in the Gibbs free energy,.

To understand this point, let us suppose that does not depend upon such as. In this case, Equation (8.5) provides

(8.6)

Substituting this in the above original Pontryaginian of, we obtain

(8.7)

This is nothing but the standard time-derivative of Gibbs free energy: Since, if we rewrite the set as and , we obtain

(8.8)

This expression means that the rate of Gibbs free energy is conserved under the time-development of the system. This proves the first part of the conjecture for the maximum principle of Motoyosi Sugita, where he assumed that M = constant for

[see Equation (7.16)]. Thus, I would like to first claim that M should be the

absolute value of the Hamiltonian in the sense of Pontryagin.

8.4. Proof of the New Conservation Law

The general proof of the conservation of the Pontryagin’s Hamiltonian is quite complex. It is not so convenient to describe the detail in short here. Since the proof is given in the text book of Pontryagin et al. [135] [136] , we skip the detail. Therefore, I would like to describe the essence of the proof.

As before, we start with the dynamics given by Equation (8.1) [or Equation (8.2)]. Let us find the equilibrium state taking the variation such as

(8.9)

where is a small positive value and we assume that the initial condition for such that it starts with the value:

(8.10)

Substituting the above into Equation (8.1), we can expand the original dynamical equations with respect to. Then, we can obtain the linearlized equations of motion:

(8.11)

The matrix is called the Jacobian or Jacobi matrix in the linear stability analysis [103] [104] [see Equation (6.29) in Section 6].

Next, let us define the adjoint matrix,:

(8.12)

And let us define the following dynamical equations for the new functions,:

(8.13)

where, t meaning transpose of. We then define the Pontryagin’s Hamiltonian as

(8.14)

Let us prove that the above Pontryaginian is a constant of motion in the nonlinear dynamical systems for the state variables. Please do not confuse that this problem is a problem for mechanical variables in classical mechanics. Although the Pontryagin’s Hamiltonian is mathematically analogous to the Hamiltonian, it is not the same physical quantity; the former represents the work rate (i.e., the power) and the latter the energy in our choice, as was mentioned before.

Differentiating with respect to time, we have

(8.15)

And we have

(8.16)

for. Substituting this into Equation (8.15), we obtain

(8.17)

Here we have assumed that the extremum condition for with respect to such that

(8.18)

By definition, this is equivalent to the following optimal condition:

(8.19)

where the maximum condition [141] is also given by

(8.20)

If the condition is for the minimum then the inequality has to be reversed.

Let us now impose

(8.21)

which is nothing but Equation (8.13), since if we take its transpose then we have

(8.22)

This equation is called the adjoint equation for the original nonlinear dynamical equations of Equation (8.11). The new set of variables play the role of the dynamical chemical potentials of the system, which depend upon time such that the values are dynamically changing according to the control variables

.

Substituting Equation (8.21) into Equation (8.17), we finally obtain

(8.23)

This means that is a constant of motion. Namely,

(8.24)

Hence, we have proven that the Pontryagin’s Hamiltonian (the Pontryaginian) is conserved in the course of time-development. Thus, the proof is obtained.

This Pontryaginian in the nonlinear systems with the state variables plays an important role of the Hamiltonian in classical mechanics. Physically speaking, this means that as long as the Power is fixed as a conserved quantity, there exists an optimal process that preserves the power.

8.5. Comparison with the Prigogine’s Method

The above approach is quite analogous to the Prigogine’s method in the nonlinear systems [103] [104] . The Prigogine’s method for the stability of the nonlinear dynamics is nothing more than the Lyapunov’s method in mathematics.

In this method, we first assume that the left hand sides of Equation (8.1) or Equation (8.2) are all zeros. This provides the following:

(8.25)

Suppose that Equation (8.25) can be solved. Solving Equation (8.25) for under fixing as, where are constants, we obtain the dy- namically equilibrium states or stationary states:

(8.26)

Similar to Equation (8.9), we expand the state vector as

(8.27)

Substituting this into Equation (8.2), we similarly obtain

(8.28)

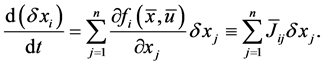
For the special values of, we define

(8.29)

Then substituting the above into Equation (8.28), we obtain

(8.30)

This yields the characteristic equation:

(8.31)

By investigating the characteristics of, we can find the stability condition of the equilibrium state such that if all real parts of the eigenvalues are negative, then the system is stable. This approach is the essence of the Pontryagin’s method. Therefore, it is nothing more than the Lyapunov method in the linear stability analysis in mathematics. This was also discussed by Motoyosi Sugita long ago such as in the subsection VI.C.

In this way, we can understand that the Pontryagin’s method in the optimal control theory is a natural generalization of the Prigogine’s method in nonlinear theory.

8.6. Generalization of the Pontryagin’s Hamiltonian to the System with a Constraint

In the above, we have proven that the Pontryagin’s Hamiltonian with state variables in nonlinear dynamics plays the role of the Hamiltonian of mechanical variables in classical dynamics. And we have shown that the Pontryagin’s Hamiltonian is a constant of motion of the dynamical system, i.e., a conserved quantity. However, we have not yet proven that the Pontryagin’s Hamiltonian takes its maximum value in the region of the admissible control parameter vectors. And we have not yet show that the principle works as well, even when there is a constraint of the system. This constraint is an- alogous to the constraint that we know as the least action principle through the Lagrangian L in classical mechanics. We are now going to consider these problems.

Suppose that there is a constraint in the system such as

(8.32)

where the time-development of the system obeys Equation (8.1) and is the n-dimensional state vector and the r-dimensional control vector.

Let us now impose that this constraint takes the minimum value in the course of the time-development of the system in between and. In other words, we expect that we are able to find the control parameter vector so that always the constraint is minimized in the course of the time-development of the system in between and. This simply means

(8.33)

The physical meaning of this is the following: We evaluate the functional of the state variables as if it were the action functional S in classical mechanics. Then, we expect that the value of the functional is always minimum possible in the course of the time-development. This constraint provides an extremum problem. In this context the functional is sometimes called the evaluation functional or the performance index (PI) in the theory of optimal control [135] [136] . So, we have to find the orbit of the state variables that obey the nonlinear dynamics Equation (8.1) such that the PI-functional must take minimum under the condition that the admissible control variables provide the maximum for the Pontryagin’s Hamil- tonian. This is analogous to the least action principle for the Lagrangian under the Hamilton dynamics for mechanical variables in classical mechanics.

In this more general case than the previous one, we can define Pontryagin’s Hamiltonian as

(8.34)

Obviously this has the form of the Hamiltonian in classical mechanics such as. Do not confuse this of Equation (8.34) with of Equation (8.7). Because the constraint of Equation (8.32) is included in the Pontryagin’s Hamiltonian in this case, while no constraint is included in the previous Hamiltonian. Therefore, I put 0 and 1 to escape from confusion. Thus, in the previous Hamiltonian the maximum can take nonzero value for M, but in the above Hamiltonian, the maximum has to be always zero [see below].

Let us now suppose the following new variable by

(8.35)

By differentiation we find

(8.36)

Let us define a fictitious parameter

(8.37)

Then we can represent the above Equation (8.34) more compactly such as

(8.38)

However, at this time the system must obey the following nonlinear dynamics:

(8.39)

As before, we then have the equations of motion similar to Equation (8.4) and Equation (8.5):

(8.40)

(8.41)

where. Here we would like to note that the first equaltion of Equation (8.41) for reduces to, since does not depend upon at all. We also have the following constraints as before:

(8.42)

where the maximum condition [141] is also given by

(8.43)

If we take then the condition becomes that for the minimum principle.

8.7. Pontryagin’s Maximum Principle

Now we can summarize the very important theorem which is known as the Pontryagin’s maximum principle in the optimal control theory [135] [136] . This theorem is described as follows:

Theorem 6 (Pontryagin’s Maximum Principle) Let us suppose that the dynamical system is described by the nonlinear dynamical equations:

(M1)

for.

Let be an admissible r-dimensional control vector in the admissible region of U given in the time interval such that the solution starts from the initial vector at time and passes a point in the line at time. Here the line is defined as a line that is parallel to the -axis and passes the point in -dimensional phase space X.

One necessary condition that control and trajectory are optimal is that according to the functions and there must exist the following non-zero continuous vectors:

(1) For all t in time interval, the function of variables u in the admissible region U (),takes the maximum at; namely,

(M2)

(2) also satisfies the following condition:

(M3)

(M4)

In practice, if satisfy the coupled equations (M1) and

(M5)

for, and satisfy the condition (1), then the function of time t, , is constant, and the function is different from the integral of Equation (M4) only by a constant amount. Therefore, Equation (M4) is sufficient to be satisfied only at some instant t in. For example, instead of Equation (M3) and Equation (M4), it is sufficient if the following condition is satisfied:

(M6)

The proof of the Pontryagin’s maximum principle is very complicated but is given in detail in the literature [135] [136] . So, we have omitted the proof here. However, the result is quite simple enough for us to apply to physical problems.

Let us go back to the case of the nonlinear dynamics with a constraint in the subsection VIII.F. In this case, is taken. Since this is nothing but the first condition in Equation (M6), we hold the second condition:

(P1)

Hence, we have the following Pontryagin’s maximum principle for this case: at some control vector value,

(P2)

8.8. The 4th Law of Thermodynamics as the Motoyosi Sugita’s Maximum Principle

Now, let us go back to the maximum principle of Motoyosi Sugita [see Equation (7.16)]. We can restate it as follows:

Theorem 7 (Modern Version of the Motoyosi Sugita’s Maxmum Principle) Suppose

that the rate of the Gibbs free energy is given as the Pontryagin’s Hamiltonian

as before. Let us define the Pontryagin’s Hamiltonian with a constraint such that

(8.44)

where the state variables are assumed to obey the following dynamical equations:

(8.45)

Then, if the system advances under the optimal control of the control variables u, then there exists a maximum of the Hamiltonian such that

(8.46)

And in this moment, always the following equations hold: The equations of motion:

(8.47)

for, the optimality condition:

(8.48)

and the maximum condition [141] :

(8.49)

Here in Equation (8.49) if then we change the inequality to such that the maximum condition becomes the minimum condition. I believe that this principle is exactly nothing more than the 4th law of thermodynamics in terms of the language of the modern control theory.

The above approach of Pontryagin’s maximum principle is very general and therefore it should not be restricted within thermodynamics. However, I would like to see the relationship between the Motoyosi Sugita’s maximum principle and the Pontryagin’s maximum principle.

Let us apply the above method to thermodynamics especially for the isothermal system where T = const. In order to do it, we must assume that the dissipated energy from the system is becoming the virtual heat such that

(8.50)

where is the dissipation function of Rayleigh [133] . This is the heart of the Onsager’s principle of the least dissipation of energy. It plays the role of Lagrangian in classical mechanics. Because when we impose that the action of energy change from the dissipation energy to the virtual heat is as fast as possible, then we take variation for it. This restriction imposes the Onsager’s variation principle:

(8.51)

or equivalently

(8.52)

Therefore, once we regard this variational constraint as in Equation (8.44), then we obtain the Pontryagin’s Hamiltonian for isothermal system as

(8.53)

where we have taken as. If we adjust with the definition of Gibbs free energy,

then we must regard the Hamiltonian in the left hand as the power. This

yields

(8.54)

This Hamiltonian was first found by the author two yeas ago [142] [143] .

Thus, as long as we take the extremum using Equation (8.46), we have to obtain the following simple relation

(8.55)

This is the most general expression for the Gibbs equation generalized from the standard one in the textbook of thermodynamics:

(8.56)

Furthermore, if we impose the quadratic relation for the dissipation function of Equation (8.50) then we substitute it into the above. We finally obtain the following relation:

(8.57)

8.9. Relationship between the Pontryagin’s Maximum Principle and the Bellman’s Principle of Optimality

Now I would like to make a comment on the relationship between the Pontryagin’s maximum principle and the Bellman’s principle of optimality (see the details in Appendix). Although both theories seem to treat the same kind of optimal problem, the apparent looking of the results is very different. Even though I can say that they are almost equivalent concepts, it is far from being trivial. Therefore, I would like to clarify this problem. This was first done by Pontryagin et al. [135] [136] .

Bellman simply assumes that there is a dynamical process whose the time develop- ment of the system is given by a time t in between the initial time and the final time. Then, he divides the interval to two regions from to t and from t to to establish the principle of optimality. However, it is not trivial. Rather, it should be unknown till we can solve the system of nonlinear differential equations Equation (8.2). In general, to solve the nonlinear equations is very difficult. Therefore, it becomes a challenging problem in physics.

Suppose that the system of the nonlinear equation of Equation (8.2) would be solved under the optimal control u for. This gives us the time interval as a function of the initial state of the system defined by the n-dimensional vector such as

(8.58)

Let us define instead of. For an arbitrary time t (), we have

(8.59)

Differentiating this with respect to t, we then derive the following:

(8.60)

For the optimal control, we have to take the optimal condition for the control parameter u. So, we finally obtain the optimality relation:

(8.61)

where U stands for the space of admissible control. This is the result that we apply the principle of dynamic programming to the system of the nonlinear equations.

Next, let us define the function:

(8.62)

Differentiating this with respect, we obviously find

(8.63)

where we have used the trivial relation by Equation (A.79). From this we have

(8.64)

Since, after some manipulation using Equation (8.64), we obtain

(8.65)

Then, if we define

(8.66)

then Equation (8.65) turns out to be the adjoint equation:

(8.67)

On the other hand, the Equation (8.61) can be written as

(8.68)

Since the left hand side of the above equation is nothing but the Pontryagin’s Hamiltonian, hence we can prove the Pontryagin’s maximum principle:

(8.69)

from using the Bellman’s dynamic programming.

Thus, as was shown by the Pontryagin’s group [135] [136] , the maximum principle of Lev Semyonovich Pontryagin in the modern control theory is essentially equivalent to the optimality principle of Richard Bellmann in the modern control theory.

9. The Motoyosi Sugita’s Theory of Metabolism: The First Application of the Maximum Principle to Life

Around the year of 1951 Motoyosi Sugita found an idea that he should apply his theory of the maximum principle to the theory of metabolism of life [38] . This was intensively studied and published in the Japanese journals [30] [31] [32] [33] [34] [41] [42] [43] [44] [45] as well as in English [61] [77] [78] [79] . Much later he generalized the idea to more complex systems of life where the control or regularity comes into the system and fortunately these were published in English [62] [80] - [87] .

In this section I would like to introduce to you the earliest version of his theory of metabolism as the application of the maximum principle.

9.1. Combined Chemical Reactions

Let us denote by the mole number for the species i of the molecule inside the body. Let us denote by the mole number for the species a of the molecule outside the body. Denote by the the reaction coordinate for the chemical reaction s in the detailed balance. Then, we define

(9.1)

where r is the number of chemical reactions and () is the matrix element that represents the production of the molecule a (i) from the chemical reaction s. If the life being is in the stationary state (or steady state), then

(9.1')

This has to mean. However, in general the state is progressing so that it is not in the stationary state; Hence,. Therefore, we can assume that isothermal chemical reactions are performed in the life phenomena.

If we denote by the molecule flowing in the body from outside and by the molecule flowing out the body from inside, the chemical motion of the matters in life is not like the water flow; it straightforwardly flows in and flows out. But it is like a complex circulation of the matters inside the body where there are reverse chemical reactions of matters and the matters are flowing out to the body. This is schematically shown in Figure 7.

This is the characteristics of life. When the system is not in the stationary state, the life itself automatically performs the cycle and adapts itself with adjusting this cycle by interacting with the external systems. Since it is not in stationary in this case, we have.

On the other hand, when we consider the stationary state, since it is not in equilibrium, local entropy production exists due to. And therefore there must exist the dissipation of the Gibbs free energy. Let us denote by the total Gibbs free energy of the system including the external system. Now we can write as

(9.2)

where and are the mole numbers of the species of molecules for the outside and inside of the system, respectively.

Now if we assume that there is no dissipation outside the body of life, then the right hand side of Equation (9.2) represents the dissipation of the Gibbs free energy. The first term means that supply from the outside to the system and waste from the system to the outside. If the system of life is in the stationary state, then they are compensate to each other. Because since, therefore. However, since the chemical cycle is performed, we divide this into two parts as

(9.3)

where the first term represents the catabolism and the second term the anabolism.

In chemical reactions in life there seem to exist three types of chemical reactions such as (i) consumption, (ii) supply, and (iii) reproduction. Thus we would like to represent them as follows:

(9.4)

where and are reaction components and and are all integers. may be. and may be the same components as well. The chemical reactions that can be regarded as the path of reactions (ii) for dissolution correspond to the main path coming from the external of the body and going out to the external of the body. The reactions regarded as (i) provide the activation Gibbs free energy and hence they are dissipative reactions. At the same time the dissipation can be compensated by reactions of (iii).

In the system of life, the above reaction are not performed independently, but they should be performed at the same time. Therefore, we can assume the following reactions:

(9.5)

Now we assume that the reaction rates (speeds) are defined by, and and so forth. We are able to assume the following expression for:

(9.6)

where

(9.7)

(9.8)

and is the chemical resistance for the chemical reaction labelled by s and, , and (, , and) are the chemical potentials for, and (,and), respectively.

Thus, once we consider in this way, the reactions are performed automatically such that the Gibbs free energies ejected from the reactions of (ii) are used for the reproduction reactions of (iii) and the dissipations of the Gibbs free energies from reproductions (namely, the Gibbs free energy produced by catabolism) are used for the progression of this combination of the chemical reaction of Equation (9.5).

9.2. Reactions of Metabolism and Maximum Principle

For the sake of simplicity, we assume the following:

(9.9)

(9.10)

This means that the Gibbs free energies produced from (ii) supply are all used for (iii) reproduction. From this situation, large energy and negative entropy are produced and they become the energy and entropy for activation. That is, so-called negative entropy has to be interpreted as activation entropy. In order that smart give and receive of the Gibbs free energies can be performed, it is not possible if the activated complex of the reacting components of the materials of (i), (ii) and (iii) takes common feature with large entropy, but it can be possible if it makes the organization with small entropy. Here is the role of proteins. Therefore, such materials like proteins thermodynamically collapse and they proceed the reactions of Equation (9.5) by give and take of the Gibbs free energy before their collapse, and constantly reproduce the materials with holding the materials that collapse are going to collapse. We have to interpret the concept of negative entropy in this meaning. The point of view of Schrödinger [147] and Brillouin [148] has a danger to recognize the negative entropy as a permanent existence.

According to Equation (9.10), the consumption (or exhaustion) per second asso- ciated with is given by. Therefore,

(9.11)

On the other hand, the reproduction per second is given by

(9.12)

Now when the system is in the stationary state, we have to hold the following relation:

(9.13)

As is discussed in the section VII, Motoyosi Sugita applied the method of maximum principle of Equation (7.16) to the above problem. Assuming that and giving the variation of, we seek for the condition that becomes the maximum. Let us define by a Lagrange multiplier (i.e., unknown parameter of Lagrange). We obtain

(9.14)

Now the relationship between and is given by Equation (9.6). We can assume that Equation (9.11) can be written in the quadratic form in the first approximation as was discussed before [Equation (7.41) in Section 7]. Within this assumption, for each s the following relation has to be satisfied

(9.15)

Here multiplying for both sides of Equation (9.15) and take the sum for s, we find

(9.16)

Comparing Equation (9.16) with Equation (9.13), we obtain. Hence, we obtain

(9.17)

or

(9.18)

This is the detailed balance equation in the process of the chemical reaction s.

From Equation (9.18) together with the help of Equation (9.1'), if we can know the ratios of between different s, then we can know the relationship between. These are the chemical potentials in the living state, and therefore, they usually cannot be measured biochemically; i.e., they are the quantities that dominate the living function biochemically.

To understand this point, let us assume that there is a material K such that it is produced by the rate of and it is consumed by the ratio of. In the stationary state, the balance of income and outgo of the material K is given by

(9.19)

As is shown in Figure 8, suppose that occurs as a combination with. If

the difference of chemical potential in each reaction is written as, then corresponding to Equation (9.18) the balance of Gibbs free energy is given by

(9.20)

Or if we use Equation (9.19) then

(9.21)

Motoyosi Sugita points out that if we write as

(9.22)

then Equation (9.21) has the same form of the equation of simple reproduction in economics, where corresponds to the utility function in economics. And hence he suggests that once we can establish the analogy between biological phenomena and economics, there appears the way to use such mathematical analysis to apply to biology.

Similarly to what was discussed on Equation (9.18), what we can say about Equation (9.21) is the following: If we are able to know the ratio between each reaction rate in the metabolism in the body with keeping the life body in the stationary state, then we are able to find the relation between the chemical potentials. From this we are able to measure the negentropy in the living state by the kinematical method. On the other hand, if we want to measure it by the usual chemical method then we have to make the living system in the equilibrium state and hence inevitably we have to kill the life. However, if we seek for the inter-relationship between the chemical rates with keeping the living chemical reactions, then we can measure the free energy of the system that is in the living state.

As a special example for the above theory of Motoyosi Sugita, he discussed the combined chemical reactions of ATP and proteins. Suppose that all protein reactions are averaged for all proteins conceptually such that we can assume that there is only one protein. Denote by the speed of decomposition of ATP to produce the protein, where the Gibbs free energy of ATP decomposed for the production of protein is given by. On the other hand, denote by the speed of de- composition of protein to produce ATP, where the Gibbs free energy of the protein decomposed for the production of ATP is given by. Then in the stationary state we have

(9.23)

where () is the chemical potential difference between decomposition and reproduction of protein (ATP) (see Figure 9). Therefore, if we can know the value of then we can know, vice versa. The free energy of proteins manufactures the complex organization of life and it makes the smart deliver and receive of the free energy possible. Therefore, once it is cut down to the outside, then the meaning of is lost. Now, according to experiments the function of protein depends on the speeds of production and decomposition.

Thus, when we think in this way, the negentropy (=negative entropy) is not permanently existing, but constantly produced by the reaction (iii), and constantly increasing by the reaction (i). If one doubts why entropy cannot increase in life body, then one forgets the combination of reactions (iii) and (i). Even though, as long as, the local production of entropy is carried out in life body.

9.3. Analogy between Thermodynamics in the Transient Phenomena and Theory of Metabolism

In the year of 1953, Motoyosi Sugita noticed some analogy between the thermal engine and the chemical engine [30] [31] [32] [33] [34] [41] [42] [43] [44] [45] [77] [78] [79] . He recognized that it is more convenient for us to consider the Gibbs free energy than to consider energy. This is because when we consider the balance of chemical energies in life phenomena, the energy is immortal forever but the free energy can be dissipated. He thought that this point is very important for life.

Suppose that there is a life system that eats foods and discharges excreta. Let us denote by the Gibbs free energy of the life system that intaking from the outside. Let us denote by the Gibbs free energy of the life system that excreting to the outside. Let us denote by D the Gibbs free energy of the system that is consumed within the system. Let us denote by the Gibbs free energy of the system that is accumulated within the system. Let us denote by its time derivative.

Now the balance of the Gibbs free energy must satisfy the following relation:

(9.24)

This equation corresponds to Equation (2.6) or Equation (3.19) in the thermal system such that and D correspond to and, respectively. On the other hand, the Gibbs free energy change for the external system (outside of the system) is given by

(9.25)

This corresponds to the Gibbs free energy change in the thermal reservoir for the thermal system such that corresponds to. Hence, the total change of the Gibbs free energy is given by

(9.26)

Since D in the life system corresponds to in the thermal system, Equation (9.26) means the 2nd law of thermodynamics for the life system. From this point of view Motoyosi Sugita intensively studied the theory of life using the analogy.

Let us now take the steady state into consideration. In the steady state, we have

(9.27)

Let us consider the detailed balance of Gibbs free energy. A part of Gibbs free energy is used to do the work of muscles or of digestion, of absorption and of excretion. Let us denote this by W. The other part is used as pump action to promote synthetic reaction or anabolism. The Gibbs free energy of our body is reproduced by this reaction. Let us denote by R the rate of reproduction. There is a loss of the Gibbs free energy during the work. Let us denote it by W. There is a loss of the Gibbs free energy during the pump action. Let us denote it by R. The rest of them is. The relation of these quantities is expressed by Figure 10.

Thus, we must hold the following:

(9.28)

Then we obtain

(9.29)

Let us define the following relation:

(9.30)

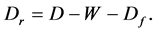
Then we have

(9.31)

9.4. Balance of Substances in Life

As a generalization of the concept of metabolic reaction, Motoyosi Sugita considered the network of the flows of substances in life systems.

Let us denote by the concentration of the chemical substance X in the chemical state of molecule i in the life system. For example, X stands for atomic elements such as C, N, etc., while i stands for complex molecules such as Amino acids, fat, etc.

Catabolism occurs in the directions from more complex molecules to simpler molecules, while Anabolism occurs from simpler molecules to more complex molecules. For the sake of simplicity, let us write the anabolism direction as in a series of, while the catabolism direction is reverse in order. Let us denote by the anabolic reaction from state to state i. Let us denote by the catabolic reaction from state i to state k, where. Now we can write the balance equation of substances as

(9.32)

This network is schematically shown in Figure 11.

In the stationary state we must have the following as usual:

(9.33)

Now let us consider the weight increase of the body of the life. This will be given by. Since the system is an open system, if we denote by the total quantity of the substances that are intaken from the outside of the body and by the total quantity of the substances that are excreted to the outside of the body, then we must have the following:

(9.34)

where w is the weight of the body. Let us denote by the quantity of X flowing from the outside into the state i in the system. Let us denote by the quantity of X flowing out from the state k to the outside. By definition the and must be defined as

(9.35)

(9.36)

respectively.

9.5. Gibbs Free Energy of Life

As described before, let us denote by the Gibbs free energy of the life system and by the Gibbs free energy of the external system. Hence, the total Gibbs free energy that includes the Gibbs free energy of the life itself is given by. The life system is a system that the total Gibbs free energy of is decreasing according to Equation (9.26).

Let us relate the quantities given by Equations (9.24)-(9.26) with the quantities given by Equations (9.32)-(9.36). Let us define the chemical potential that X belongs to the state i by

(9.37)

From this we can define the rate of the Gibbs free energy of the life system by

(9.38)

Now substituting Equation (9.32) into of Equation (9.38), we obtain

(9.39)

This can be converted into the following form:

(9.40)

where and are given by

(9.41)

(9.42)

respectively. In Equation (9.40), represents the anabolic reaction when, while represents the catabolic reaction when . is the Gibbs free energy of the intake of food while is that of waste from the body of the life. Thus we can consider that the food is absorbed with the chemical potential and the waste is ejected with the chemical potential. Hence, the difference is equivalent to the metabolic energy.

Now if we define D as

(9.43)

then we obtain

(9.44)

This is nothing but Equation (9.29). In the stationary state it provides the following:

(9.45)

Thus, we have been able to represent the quantities for the life system such as, , and in terms of the quantities in the biological chemical network such as, , and.

This is the essence of the Motoyosi Sugita’s theory of metabolic network system, which was entitled as Metabolic Turnover of Entropy and Energy and its Mathematical Analysis in Life I-V. It was first published in Japanese in the Busseiron Kenkyu [30] [31] [32] [33] , which was also published in English in the Journal of Physical Society of Japan [61] [77] [78] [79] , and later the generalized version of the theory was published in Japanese in the Bulletin of Kobayasi Institute as well as in the Busseiron Kenkyu [34] [41] [42] [43] [44] [45] . I would like to strongly recommend the Western people to read his theory published as the English papers [61] [77] [78] [79] .

9.6. The Birth of Network Thermodynamics

The above Motoyosi Sugita’s theory of metabolic network in the life-being system is much earlier than the network thermodynamics that was founded by Aharon Katchalsky’s group [106] [108] as earlier as 20 years. As one of the coworker of Lars Onsager, Aharon Katchalsky with his students George F. Oster, and Alan S. Perelson independently developed the extension of the Onsager’s theory of irreversible processes to the theory of life system. They found the relationship between the network of chemical reaction in biosystems and that of electrical circuit in electronics. Hence, they named their theory the network thermodynamics.

The starting point of Aharon Katchalsky’s group is Equation (7.32):

(9.46)

where in order to adjust with their notation, I have used in stead of in Equation (7.32). They took this as the fundamental equation for their theory of network thermodynamics.

Let us suppose that there is a biochemical network system that is represented by a network graph such as Figure 11. Let us assume that we define chemical potential on the i-th node of the graph and the current on the link in the graph, respectively. Let us assume that there is the standard chemical potential that can measure the standard level for the chemical potentials. This is analogous when we consider the electrical circuit where the ground point plays the role of the standard level for all the potentials.

By using this problem-setting, they found the Kirchhoff’s law in biosystems, where there are the Kirchhoff's current law (KCL) and Kirchhoff’s voltage law (KVL). The KCL is the conservation law of the currents on a node such that the total amount of incoming currents to the node must be the same as the outgoing currents from the node. The KVL is the conservation of the voltages (or the potentials) along any closed circuit in the network graph. Obviously these are very common knowledge in the elementary circuit theory or the elementary electromagnetism. Hence there is no need to explain much more. However, although there is a very famous theorem in the circuit theory that is called the Tellegen’s theorem [149] - [154] , this is not so well known among physicists except some experts in electronics, although it is a natural gen- eralization of the theorem of the Joule’s least heat in the steady current or the Thomson’s theorem in the static electric field [155] .

The Tellegen’s theorem states the following: Let us denote by the current flowing out from the node i and flowing into the node j in the link ij. Let us denote by the voltage difference between the the node i and the node j. When both the KCL and KVL are satisfied at the same time for an arbitrary network graph of electrical circuit, if we represent the current vector and the voltage vector by

(9.47)

(9.48)

then the following relation must be satisfied:

(9.49)

where t stands for the transpose of the vector. This simple and rather looking trivial relation of Equation (9.49) is called the Tellegen’s theorem. And it is really a very powerful tool in the electrical circuit theory [149] - [154] .

What is important here is that Aharon Katchalsky’s group has found that Equation (9.46) in the biochemical network system is equivalent to Equation (9.49) in electronic circuit systems. Let us represent the in Equation (9.46) in terms of the differences in the chemical potentials where the level chemical potential is denoted by. It is given by

(9.50)

The rate of the Gibbs free energy of the system, , is given by

(9.51)

From Equation (9.46) we obtain

(9.52)

If we explicitly write down the KCL and the KVL for a given network graph and if we use the relations of the KCL and the KVL, then we can prove that the above Equation (9.52) can be converted into the form of Equation (9.49). This is the findings of Aharon Katchalsky’s group [106] - [112] .

I would like to put a comment here. There is a difference between the Motoyosi Sugita’s approach and the Katchalsky’s approach. In the former, Motoyosi Sugita used the concept of field of chemical potential and therefore, the current flow is given by

(9.53)

while in the latter Katchalsky’s group used the Onsager’s linear relation or the De Donder’s linear relation:

(9.54)

where T is the temperature of the system, k is the Boltzmann constant, is the chemical resistance, and is the chemical potential on the j-node in the network graph. According to the chemical reaction:

(9.55)

the above chemical potentials are defined as

(9.56)

Very very sadly Aharon Katchalsky(Aharon Katzir) was killed by terrorism of the Japanese red army at the Ben Gurion International Airport in 1972. He was one of the victims when 26 people were killed by the attack. I feel very sorry for that. I would like to state that Rest in Peace to him and others. Therefore, actually the year of 1972 is the end of his theory. Later on, Perelson and Oster had followed the line of Katchalsky straightforwardly and extended their theory to more complex network systems [106] - [112] . However, their theory became very pure mathematical so that none can easily follow them. Hence, the Katchalsky theory seems dead at that time. However, recently some people noticed the importance of the Katchalsky’s work and applied to the membrane system of life [156] [157] and the complex metabolic network [158] [159] as Motoyosi Sugita did it long long ago as early as 65 years. This would be regarded as some revival for their theory.

As was discussed in Section 7, the reason why we must have Equation (9.46) lies on the fact that there exists the 4th law of thermodynamics in nature from the view point of Motoyosi Sugita. It is realized as the maximum principle for the transient pheno- mena such as life phenomena. The concept of the transient phenomena is much broad concept than that of the irreversible processes studied by Lars Onsager and Ilya Prigogine as well as Aharon Katchalsky. The maximum principle for the transient phenomena always works as the 4th law of thermodynamics in biological phenomena such as metabolism. So, the equation such as Equation (9.46) appears as the Tellegen’s theorem in the circuit theory and in the biological network theory as well.

10. The Motoyosi Sugita’s Theory of Thermodynamics of Life

10.1. The Phenomena of Life and Its Analogy to Social Economics

In the English paper of 1954 [61] , Motoyosi Sugita pointed out the resemblance of the phenomena of life and the social economics, since the life phenomena can be regarded as the society of molecules in cells or that of cells as follows.

1) Our body consumes various organic and inorganic substances, some of which are produced in our body, like hormone, enzymes, protein, nuclear acid, fats and others, and some of which are taken from the external world by the work of our muscles and digestive organs, like inorganic salt, vitamins, amino acids and others.

2) These substances are useful to maintain life. The idea of nutritive value is well known but quantitatively the value of caloric units is mainly taken into account. The nutritive value of vitamins, iron and other inorganic substances and some amino acids is also taken into account but only qualitatively. There may exist the idea corresponding to utility or welfare function in economics which may be treated analytically and quantitatively.

3) There is consumption of Gibbs free energy (shortly say, F. E.) to produce or absorb the necessary substances and consumption is required by production and intake. Even the absorption of glucose, which is the last stage of digested starch is carried out by the investment of F. E. of ATP, an ester of phosphoric acid of high energy. Therefore, in the case of famine or when ill-fed, our organ loses the power to digest or absorb nutritious substances due to the lack of F. E., which corresponds to initial cost. On the contrary, the function of intestinal absorption will be dangerously damaged if over-fed.

The above is shown in Figure 12, in which the energy is fed back to take the chemical energy from the external world. This feeding back is similar to business life, in which an enterprise is sometimes suppressed by the lack of the initial cost. Indeed our

body corresponds to a factory and ATP to capital.

4) There is the balance of the need and the supply. Superfluous protein, for instance, loses its amino-group and changes into carbon-hydrates corresponding to consumer’s goods. On the other hand, the protein of our tissues, which corresponds to producer’s goods, is destroyed by lack of protein, and the material is used to construct the other necessary part.

According to Professor Kida the relatively short legs of the Japanese are due to the lack of protein of high quality in food during growth. The body seems to lack protein to build legs, for we must use the material to construct the necessary part of our organs. Medical science may be considered good management in the balance of matter and F. E.

5) Our body corresponds to our system of industry. Various substances are produced in every part of our body and supplied to other parts. On the other hand, the parts are also supplied from other parts. There is an exchange and economy of matter and energy. For instance, the production of protein corresponds to the first department of pro- ducer’s goods. In this case as well ATP as protein is consumed. The consumption of the latter corresponds to the depreciation of producer’s goods, in this case the chemical apparatus made of protein.

The ATP which is consumed, is reproduced again in our body and carbon-hydrates, protein and ATP are consumed for reproduction. Here, the carbon-hydrates corre- spond to consumer’s goods and the reproduction of ATP to the second department of economics. Therefore, there is a close analogy between the two fields. For instance, labour is reproduced by the consumption of goods, just as carbon-hydrates in food. This fact is important from the point of view of methodology (see Figure 9).

On the other hand the consumption of protein which is an example of catabolism, corresponds to depreciation which is repaired by anabolism.

6) Depreciation and the repair is the general aspect of life. For instance, reproduction is the turnover of the body itself, which depreciates during life, especially by re- production itself.

If we take, however, the history of man-kind into account, depreciation in the individual body is repaired by other bodies. Therefore, those who enjoy youth enjoy the turnover of the individual body.

Therefore, one of the most prominent aspects of life is the turnover of molecules of cells and of the individual body, so that the world of the living organism is repaired and steadily maintained. This is very important from the point of view of thermo-dynamics, for the F. E. on earth is constantly consumed by organisms.

The steadiness is similar to that of the river, which consumes the potential energy of water and also maintains steadiness on the balance of water.

In a similar manner the depreciation of the apparatus of a chemical plant, the value of N. E. (negative entropy) of our body is also depreciated (c.f., see Section 9). On the other hand this value of N. E. regulates the value of F. E. of activation of bio-chemical reactions. Therefore, the catalytic action of the organs, corresponding to the function of the chemical plant, is also depreciated and repaired. In this respect the writer has introduced the idea of the metabolic turnover of N. E., corresponding to the depre- ciation and the repair of producer’s goods in economics.

7) Besides the feed back of F. E. there is the circulation of matter in our body, for instance the chemical cycle of ATP€ADP or the reduction and oxidation of enzymes. Figure 13 shows the circulation of phosphates of adenosine in which ATP is included. The circulation is very complicated, in general, but is schematized in Figure 7. This is similar to the circulation of paper money in our society. In a similar manner, the matter of high energy is taken from the external world and excreted, so that our body corresponds to a pipe and is called an open system. But it is not an open system like the pipe through which the water of a tank flows.

8) The feedback of matter and energy is very similar to the management of our social life. Chemical processes in our body are combined like the system of gears (c.f., see Section 9), and, if we wish to promote a process, the effect is fed back and produces sometimes unexpected results. Here is the difference of the biochemical change from that in vitro. Therefore, if the knowledge of chemistry in vitro is applied mechanically the effect may be contrary to expectation, as in the controlled social economy.

There is bad circulation in our body. For instance, the appetite is diminished, if health is destroyed, and health is disturbed if the appetite is diminished. Good management by the physician will eliminate bad circulation.

9) There is the balance and stability of matter and F. E., in our metabolism. If the balance is disturbed,the function of our body is disturbed. We have seen that our body resembled a pipe, through which the matter of high chemical energy flows and the matter of low chemical energy is excreted. The balance seems to be favorable to the flow of matter (see Figure 14). In social life the balance of production and consumption is favourable to the movement of goods. There is the recovering action in our body as well

as in our society. If the balance is disturbed, and cannot be recovered, a catastrophe occurs and finally death of our body.

Prof. Bertalanffy [161] [162] [163] called the balance of our body dynamic stability or equilibrium. From the point of view of thermodynamics, this is not thermal equilibrium. But stability can be seen in many transient phenomena of the inanimate world. I have studied such phenomena from the point of view of molecular statistics and noticed the stable equilibrium of the second coordinate which will be discussed later (c.f., see Section 9) in connection with the maximum principle.

10.2. Motoyosi Sugita’s Inclination and Devotion to Incorporate Cybernetics of Norbert Wiener

After 1957 when I was born in Kofu, Japan, Motoyosi Sugita turned the direction of his bio-theoretical work to incorporate the cybernetics of Norbert Wiener [164] [165] [166] . There seem to be several reasons for it.

1) First, Motoyosi Sugita got stuck on his way to prove the maximum principle for the existence of the 4th law of thermodynamics around 1957;

2) Second, there suddenly emerged a world-wide upheaval of cybernetics of Norbert Wiener around the time;

3) Third, he became to see more importance on the regulation such as feedback control introduced by Norbert Wiener and digital control than on the nonequilibrium thermodynamics in the transient phenomena;

4) Fourth, among other things, his concept of field of chemical potential [see Equation (6.9), Equation (7.36), Equation (9.6)]:

(10.1)

was very easy to adjust with cybernetics. Here the chemical resistance plays

the role of the regulation nozzle in the regulator process.

5) Fifth, the concept of cybernetics is so broad that it fascinated him very much, since he was a full time professor for economics and economical management in the Hitotsubashi University which is one of the top national universities for the humanities course in Japan.

6) Sixth, his time was a bit earlier than the era of modern optimal control theory. I believe that this would be the main reason for that.

As is known that cybernetics as well as feedback control of Norbert Wiener belong to the classical control theory, we know the modern control theory such as L. Pontryagin’s maximum principle [see Section 8] and Richard Bellman’s optimality principle (see Appendix) nowadays. Motoyosi Sugita was born in the age of classical control theory much earlier than that of modern control theory. Therefore, he seemed unfamiliar with what happened in the control theory around 1960 when Pontryagin’s revolution occurred. So, he would like to catch up the Norbert Wiener’s theory for his theory of thermodynamics of life.

The above situation seemed to stimulate Motoyosi Sugita to write many books on the application of cybernetics to the theory of life or life being [5] [6] [7] [8] [10] [11] [12] . For the English world, he published many papers on it around 1960-1975 [62] [80] - [87] . Only one of them (1963’s paper) was cited in Stuart A. Kauffman’s The Origins of Order [99] .

Although this research theme is very fascinated, this is out of scope of this paper. Otherwise, more several hundreds pages would be needed to do it. This work would be for you, the readers, probably not for me, I hope!

11. Conclusions

In conclusion, I have introduced the personal history of Motoyosi Sugita in Section 1. Here I summarized his birth, education, working, marriage, visits, publications, as well as his research history, etc.

In Section 2, I have shortly summarized his bright ideas of the concept of broad quasi-static change, the concept of virtual heat, and the concept of irreversible cycle. And I have shown his application of them to a certain classical phenomenon in physics such as the Kelvin’s thermoelectric effect.

In Section 3, as another example for his application to other classical phenomena in physics, I have discussed the diffusion phenomena. Here the Langevin equation, the mixing entropy and free energy, the number of partition have been discussed.

In Section 4, the theory of condensation in the supersaturated state developed by Becker-Döring, Volmer, and Frenkel has been discussed. I explained that this theory promoted Motoyosi Sugita to recognize the importance of the concept of the field of chemical potential.

In Section 5, I have summarized Motoyosi Sugita’s thermodynamics of transient phenomena. Here for the concrete understanding, the theory has been applied to the chemical reactions only. Considering the system of chemical reaction network, the concept of the field of chemical potential, the relationship between cooperative phenomena and the chemical potential have been discussed.

In Section 6, I summarized the maximum principle of Motoyosi Sugita in the transient phenomena. Here I have discussed = max conjecture, the existence of the 4th law of thermodynamics, the relationship between the Boltzmann’s H-theorem and the m-field (i.e., the field of chemical potential). Also, the proof of the conjecture was shown for some special situation.

In Section 7, I have argued the relationship between the Motoyosi Sugita’s theory and the theories of Lars Onsager and Ilya Prigogine. Here in general, both of them are almost identical and therefore they established the same type of theory independently. However, while the Onsager-Prigogine’s theory was limited within the linear theory, Motoyosi Sugita’s theory went far beyond the linear theory using the concept of the field of chemical potential.

In Section 8, I have discussed the relationship between the maximim principle of Motoyosi Sugita and that of Pontryagin in the modern optimal control theory. I have shown that the Motoyosi Sugita’s approach can be absorbed into the more broad category of Pontryagi’s theory. And therefore, the way to prove his conjecture lies on the fact that the Pontryagin’s maximum principle can be regarded as a key to prove the existence of the 4th law of thermodynamics when it is applied to non-equilibrium thermodynamics in the transient phenomena. I also have shown the Bellman’s principle of optimality (see Appendix).

In Section 9, I have shortly summarized the first application of the Motoyosi Sugita’s maximum principle to the theory of metabolism. Here I have discussed the combined chemical reactions, reactions of metabolism, and the maximum principle, the analogy between thermodynamics in the transient phenomena and the theory of metabolism, the balance equation of substances, the Gibbs free energy of life, the birth of network thermodynamics, respectively.

In Section 10, I have shortly introduced the Motoyosi Sugita’s theory of life. Here I have shown his way of thinking on the topic, quoting his main explanation on his motivation. Finally, I have presented the Motoyosi Sugita’s work of theory of life adapting cybernetics of Norbert Wiener after 1957.

Looking back at my long journey to introduce the widely unknown Japanese thermodynamicist, Motoyosi Sugita, to the Western world (namely, the English- reading people) as well as to the young generations of biophysical scientists in Japan, what I have done here seems far from to be perfect. However, being insufficient is much better than nothing to do. All that glitters is not gold. If what I have done here would help you to understand the great work of Motoyosi Sugita, then I could sleep well. This is only just a beginning for the construction of theory of life.

Acknowledgements

I would like to thank Dr. Jewgeni Starikow, Dr. Hiroaki S. Yamada and Dr. Hirohisa Tamagawa for useful communications and for their help in collecting Dr. Motoyosi Sugita’s very old research papers. I would like to thank Dr. Kazuhiko Aomoto for his useful comments and suggestions on mathematics. I would like to express my special thanks to Ms. Noriko Terui of Sōtōshu Hōjōji for providing me many books and scientific papers written by Dr. Motoyosi Sugita. I have no word to express my sincere thanks to Ms. Noriko Terui when I had to find the relative of Dr. Motoyosi Sugita and his wife. I was totally and perfectly owed by her for that. And I finally found Ms. Setsu Honda as the Motoyosi Sugita’s last relative. I would like to thank Ms. Setsu Honda for private communications on the history of Dr. Motoyosi Sugita and his family and for providing me several pictures of Motoyosi Sugita and accepting them for presenting in public. I learned from her that Dr. and Mrs. Sugita had only one son Yūkichi who passed away in the 2nd day of August 2012 and hence there is no descendant for them. I would like to thank my son Jōji Iguchi for finding first Dr. Motoyosi Sugita’s textbook of thermodynamics in Kobe University and thank my elder son Issaku Iguchi for his encouragement. Finally I would like to thank my wife Kazuko Iguchi for her constant support and encouragement and for sharing our life for a long time. I could really enjoy writing this paper.

Cite this paper

Iguchi, K. (2016) Motoyosi Sugita―A “Widely Unknown” Japanese Thermodynamicist Who Explored the 4th Law of Thermodynamics for Creation of the Theory of Life. Open Journal of Biophysics, 6, 125-232. http://dx.doi.org/10.4236/ojbiphy.2016.64012

References

Appendix: The Bellman’s Theory of Optimality Principle

The Richard Bellman’s work in engineering mathematics and control theory has not so well-known in physics community as well [137] [138] . However, it is also very important for our purpose as well as so is Pontryagin’s theory. As is shown before, on the one hand, Pontryagin’s theory is the generalization of the Hamilton principle in classical mechanics to the theory of optimal control. On the other hand, Bellman’s theory is the generalization of the Hamilton-Jacobi theory in classical mechanics to the theory of optimal control, whose theory is called the dynamic programming in the control theory [137] [138] . From the quality and flavor of Bellman’s work and the age that the work was done, I feel like that he is “Richard Feynman” [145] in engineering mathematics. Even their faces are alike to each other as well.

1. Multistage Processes

The expression of the multistage processes is that in the optimal control theory and in the applied mathematics. It is nothing more than the recursive processes and the iteration processes in physical terminology.

Now, let us denote by a state vector x a point in an n-dimensional space. Next, let us consider that the point is transformed into another point by the transformation function. Namely,

(A1)

By repeating this process, the transformation from the n-th stage to the -th stage is written by

(A.2)

Thus, as the initial point flutters from point to point till it moves to the final point, we finally obtain an infinite series of the points. That is,

(A.3)

We call this multistage process. It is inconvenient to write many terms in the series at every time, we write it in the simplified way:

(A.4)

2. N-Stage Processes and Reduction of Data

Since we human being control the system in the optimal control theory, we consider the case of finite time. Therefore, we assume that there is an upper limit number N in the sequence. That is, we consider only the case:

(A.5)

Then, later we take the limiting process:. If we write it much more mathematically reasonably, we have

(A.6)

Now, we consider that there exists a function in this multistage process. In other words, we consider that a function g is written in the following:

(A.7)

This is thought of as a mapping from the coordinates in the very higher dimension onto the scalar function. It is a projection, which deletes many data by this mapping. Therefore, it reduces the data in a sense. What we represent the multistage processes by a function means that we have performed reduction of the data.

As explicit examples, the following forms can be considered:

(A.8)

(A.9)

3. N-Stage Deterministic Process and Mathematical Representation of Policy

Let us consider the expression of the N-stage deterministic process in the optimal control theory and in the applied mathematics [137] [138] . It is nothing more than the recursive processes and the iteration processes in physical terminology.

Now, let us denote by a state vector x a point in an n-dimensional space. Let us denote by u the r-dimensional vectors for control variables that we determine at each stage. Then, an N-stage deterministic process is given as follows:

(A.10)

where we have defined. This produces a vector sequence:

(A.11)

Let us now define the evaluation function or the performance index function by:

(A.12)

In the theory of optimal control [135] [136] , the above external vector u is called the control vector or the control function. On the other hand, in the theory of dynamic programming [137] [138] , it is called the policy or decision.

4. Mathematical Representation of Policy

The evaluation function is a function of the state vectors and the policy vectors from the initial state to the final state. But in order to decide the policy at any stage, the policy itself have to be evaluated by them. Therefore, the policy must be thought of as a function of the past state vectors and the past policy vectors such as

(A.13)

This is called the policy function. When the policy makes the evaluation function optimal, we may call it the optimal policy. And the optimality problem is that to determine the optimal policy by the multistage processes.

The above case of Equation (A.13) is most general, since it includes all the information of the past. Therefore, it is very complicated, since the policies in the past determine the present policy. So, we have to simplify the policy representation by restricting ourselves to consider only the case that the state is determined by the state in the past just before the present time, such as the law of causality. In this restricted case, we have

(A.14)

Or for a bit more complicated system, it is given as

(A.15)

where is defined by

(A.16)

When we adopt the condition such as Equation (A.14) or Equation (A.15), the evaluation function can be written as a sum or a product of the function of local specific variables. In this case we recognize that the separability of the evaluation function is realized. The evaluation function can be written in the following:

(A.17)

(A.18)

5. Independency from the Past and Mathematical Representation of the Law of Causality

The multistage process (that is, the recursive process) always depends upon only the state one step before. Although the past, the present and the future are all connected in time series, the present state is determined by the past state one step before. This is the concept of the multistage process. Therefore, the present is nothing to do with all the past before the past one step before. In this sense, the present is independent of the past.

Mathematically, it is given by

(A.19)

which means

(A.20)

This is the so-called mathematical representation of the law of causality.

6. Mathematical Representation of the Law of Causality

We now define the mathematical representation of causality. Suppose that the state of the system is at time t, where is the initial state of the system. Suppose that the system is progressing from the initial state to the final state at time.

At this moment, we can separate the whole interval from the initial time to the final time into two intervals: one region is the interval between and t and the second is the interval between t and.

In the first interval the state lies in at time, and it goes to the state at time t. In the second interval, the system is progressing from the state at time t to the final state at time. However, the final state is equal to the state that the system starting from the state at time t becomes the system progressing to the state. Thus, we are able to adopt the causality condition that

(A.21)

7. Recursive Processes

When we consider the systems of engineering or physics, we evaluate a function that emerges by an engineering process or a physical process. We calculate the physical quantity, according to the process that the state of the system changes at a time. This becomes the main theme for us.

Now, we call such physical quantities the evaluating function or the performance index in the control theory. Let us denote it by. For example,

(A.22)

By the way, for the terms of, we know

(A.23)

Therefore, the first relation becomes

(A.24)

This is a functional equation of. It is the recursive equation.

Assuming that the system start at the initial state x, if we want to find the maximum of the evaluation function

(A.25)

then we can derive

(A.26)

This is called the Bellman’s equation for dynamic programming.

8. Infinite Process, Time-Dependent Process, and Non-Stationary Process

The process with the limit is called an infinite process. This is the process that we take care of this limit in the above all procedures before.

And we consider that transformation function R is always the same so far. But we may think that the transformation function can change at each step. It is the time- dependent process. That is,

(A.27)

Furthermore, in the non-stationary process:

(A.28)

we have

(A.29)

If we can consider

(A.30)

then we have

(A.31)

9. Continuous Multistage Process

We have considered the discrete multistage processes so far. The discrete multistage processes that are generalized to the cases of the continuous time are the continuous multistage processes. In this case, if we divide the time very many:

(A.32)

then we can treat the process as if it is a discrete process, and then finally we take the time interval to the limit of 0 (i.e.,).

The transformation function is considered up to the linear term of.

(A.33)

We consider the evaluation function up to the linear term of as well. That is,

(A.34)

Therefore, the recursive relation in this case is

(A.35)

Expanding both sides of the equation, and comparing the linear terms, we obtain the following:

(A.36)

This is the functional relation for the continuous multistage process. Physically considering, it is nothing but the Fokker-Planck equation [146] when the external force exists, where corresponds to the velocity.

As is discussed before, if we want to obtain the maximum of the f, we need find the solution of the following equation:

(A.37)

This is called the Bellman’s differential equation.

10. Principle of Optimality and Bellman’s Optimality Equation

Bellman introduced the principle of optimality [137] [138] , which is described in the following principle:

Principle of optimality:

An optimal policy has the property that whatever the initial state and the initial decision are, the remaining decisions must constitute an optimal policy with regard to the state resulting from the first decision.

This principle is a very general property and has universality. And we can say that this principle of optimality is equally matched for the Dirac-Feynman’s principle for the path integral in physics [145] .

For example, we consider the following evaluation function:

(A.38)

This is the function that this physical quantity provides data when we decide whether or not the maximum effect is attained in the multistage deterministic process. We decide whether the process is effective or not through evaluating this function. Namely, we determine so that the function becomes maximum. Therefore, we denote by the function when it becomes maximum:

(A.39)

Since we assume that we decide the optimal policy at each step from the principle of optimality, we have

(A.40)

Comparing this for, we get

(A.41)

The initial state is defined by

(A.42)

Similar functional equations are obtained for other multistage deterministic pro- cesses as well. In general we call these the Bellman’s optimality equation.

11. The Meaning of the Principle of Optimality and Dynamic Programming

The meaning of the principle of optimality and dynamic programming is as follows: In general, the evaluation function is a problem of the two-point boundary value of the initial and final states such that we have to consider all processes in between the interval.

In classical mechanics, we impose that the action function S becomes minimum between the initial and final states under the principle of least action. This provides the Euler-Lagrange equation for the orbit. Conversely, once the Euler-Lagrange equation is written down, we would like to solve the Euler-Lagrange equation. This provides the temporal motion of the orbit in between the two boundary times, which guarantees that the action S becomes always minimum.

On the other hand, in the theory of optimal control, we impose that the evaluation function becomes maximum between the initial and final states as the principle of optimality. This provides the Bellman’s equation of optimality for the state. Conversely, once the Bellman’s equation of optimality is written down, we solve the Bellman’s equation. This provides the temporal development of the state in between the two boundary times, which guarantees that the evaluation function becomes optimal.

In this sense, the Bellman's principle of optimality is the natural extension of the principle of least action in classical mechanics. In the automatic control engineering and the control theory, to determine the policy at each stage is called the dynamic programming. The Bellman’s dynamic programming provides the algorithms to give the optimal evaluation at each stage of the process.

Inversely, we can think that the Euler-Lagrange equation of motion is the algorithm that determines the orbit of the classical object in order to give the optimal action at each time. The evaluation function in classical mechanics is the action function and the evaluation function in the optimal control theory plays the same role as the action in classical mechanics.

12. Continuous Multistage Deterministic Process

We have considered the discrete multistage deterministic processes so far. The discrete multistage deterministic processes can be generalized the continuous multistage deter- ministic processes. In this case, if we divide the time interval into very many small intervals of, we can use the idea of the discrete time:

(A.43)

Then we can treat the process as if it is a discrete process, and at the end we take the limit of.

Let us assume. Suppose that the policy is fixed as u. The transformation function [see Equation (A.1)] is considered up to the linear term of.

(A.44)

where and are the n-dimensional vectors. The evaluation function is given by

(A45)

And we denote by the maximum of the evaluation function such that. Since, we can regard it as a function of continuous time t such as.

We consider the evaluation function of Equation (A.39) up to the linear term of:

(A.46)

Therefore, the recursive relation Equation (A.40) becomes

(A.47)

Expanding both sides of the equation up to the linear order of, and comparing the coefficients of the linear terms, we obtain the following:

(A.48)

This is the functional equation in the continuous multistage deterministic process. This is called the Bellman’s partial differential equation. Physically speaking, it is nothing but the Fokker-Planck equation [146] when the external force exists, where corresponds to the velocity.

In the above we have considered the final time as a free parameter of T. However, since we can regard the initial time as a free parameter, in this case we can just replace as. Then, the corresponding equation becomes

(A.49)

This corresponds to the Hamilton-Jacobi equation in classical mechanics, since the and the second term in the left hand side corresponds to the action integral and the Hamiltonian in classical mechanics, respectively. Therefore, we can call it the Bellman’s Hamilton-Jacobi equation. This point will be discussed more explicitly later.

13. Relationship between the Variational Principle and the Dynamic Programming

At first glance, the functional equation of the dynamic programming for the continuous multistage deterministic process looks totally different from the Euler-Lagrange equation of motion in classical mechanics. We can prove that they are equivalent to each other, however.

For the sake of simplicity, let us consider the following evaluation function with one-dimensional state vector:

(A.50)

where. The value that the evaluation function is maximum is given by

(A.51)

The state variable is at some fixed time t, and time left for the process becomes. In the usual case of the variational problem, corresponding to the velocity (i.e., the tangent) becomes the determination of the policy.

Let us consider the problem to determine the initial tangent. If we denote it by u, then the integral interval can be separated into the following two regions:

(A.52)

In the first interval,

(A.53)

The principle of optimality is described as

(A.54)

Therefore, we have

(A.55)

This functional relation determines both the maximum of the integral and the policy function.

Now, putting here and calculating the right-hand side of the above equation, namely, differentiating inside with respect to u in order to obtain the maximum, we have

(A.56)

This is the condition to get the maximum. To satisfy the principle of optimality is to require that always this condition is satisfied. Therefore, if we think that this condition is always satisfied, then we get rid of in the right-hand side. Hence, we have

(A.57)

Differentiating both sides of Equation (A.56) with respect to time,

(A.58)

Similarly, differentiating both sides of Equation (A.57) with respect to q,

(A.59)

Comparing both results, since each right hand side is identical, we finally obtain the Euler-Lagrange equation:

(A.60)

In this case of the variational problem, we are not able to understand whether or not the original evaluation function takes the maximum value or the minimum value only from the extremum condition for the variation in the linear order. And the condition of Legendre is the condition that guarantees it; Namely, for the case of the maximum (minimum), we hold

(A.61)

In classical mechanics it is very difficult to put the restriction on the policy and it is not necessary to do so. However, in the dynamic programming and in the optimal control theory, there are various ranges and restrictions of the policy.

For example,

(A.62)

In such a case, since the principle of optimality is satisfied, we change the problem to the one that we seek for the maximum with a constraint. That is,

(A.63)

14. Geometrical Meaning of Dynamic Programming

The geometrical meaning of the dynamic programming is as follows: In classical mechanics we seek for the curve corresponding to the orbit in the mechanical system. We select the orbit so that the action becomes maximum or minimum. Therefore, the unknown function u is regarded as a point in the functional space. On the other hand, in the dynamic programming, we seek for the optimal direction at each instant. The solution is represented by the envelope curve that is constructed by collecting the optimal directions selected at each point. Namely, it turns out to be the envelope of its tangents of the curve. Using the terminology in fluid mechanics, it corresponds to the streamline. In this respect, the variational principle in classical mechanics is dual to the principle of optimality each other. Hence, we find the duality between the variational principle and the principle of optimality.

15. Hamilton-Jacobi Equation

When we apply the principle of optimality to classical mechanics, the problem of optimal control reduces to solve the Hamilton-Jacobi equation [137] [138] [139] [140] . Consider the action integral I:

(A.64)

where L is the Lagrangian. When the action integral takes the minimum, we write as

(A.65)

Similarly as before, we divide the whole interval of time into two intervals and:

(A.66)

In the limit of, we have

(A.67)

Differentiating inside with respect to yields

(A.68)

And from this, we find

(A.69)

is the momentum vector at.

Now, this time if we apply the principle of optimality for the state x not at the initial time but at the final time t, then the terms that depend upon the time derivative change its sign to minus. Therefore, we obtain the following:

(A.70)

(A.71)

(A.72)

(A.73)

Thus, if we define the Hamiltonian H by

(A.74)

then we get

(A.75)

This is again the Hamiltonian-Jacobi equation in classical mechanics.

Thus, when the idea of the Bellman’s principle of optimality is applied to the special case of the action function in classical mechanics, then it reproduces to the usual the principle of least action. In this respect, the Bellman’s principle of optimality is thought of as being a natural generalization of the principle of least action.