Open Journal of Composite Materials
Vol.06 No.01(2016), Article ID:62956,12 pages
10.4236/ojcm.2016.61004
On the Impact of Manufacturing Uncertainty in Structural Health Monitoring of Composite Structures: A Signal to Noise Weighted Neural Network Process
Hessamodin Teimouri1, Abbas S. Milani1, Rudolf Seethaler1, Amir Heidarzadeh2
1School of Engineering, University of British Columbia, Kelowna, Canada
2Department of Aerospace Engineering, Sharif University of Technology, Tehran, Iran

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 11 November 2015; accepted 19 January 2016; published 22 January 2016
ABSTRACT
This article investigates the potential impact of manufacturing uncertainty in composite structures here in the form of thickness variation in laminate plies, on the robustness of commonly used Artificial Neural Networks (ANN) in Structural Health Monitoring (SHM). Namely, the robustness of an ANN SHM system is assessed through an airfoil case study based on the sensitivity of delamination location and size predictions, when the ANN is imposed to noisy input. In light of the observed poor performance of the original network, even when its architecture was carefully optimized, it had been proposed to weigh the input layer of the ANN by a set of signal-to-noise (SN) ratios and then trained the network. Both damage location and size predictions of the latter SHM approach were increased to above 90%. Practical aspects of the proposed robust SN-ANN SHM have also been discussed.
Keywords:
Composite Structures, Manufacturing Uncertainties, Structural Health Monitoring, Artificial Neural Networks, Signal-to-Noise Weighting

1. Introduction
The cornerstone of Structural Health Monitoring (SHM) in engineering design is the comparison of data measured over a pre-defined damaged structure to the same type of information obtained from the healthy (un-dam- aged) structure, when subjected to identical loading/testing conditions [1] - [4] . A main goal in SHM is to seek for abnormalities in the structure’s behavior and try to classify or correlate them to the location and extent of damage during the actual service of the same or a similar structure. For this purpose, the machine learning techniques have been developed and widely used by researchers and industry experts [1] , by means of simulating the learning ability of humans via computer algorithms to analyze the measured input data and gain the corresponding (output) knowledge and skills. More specifically, the ultimate purpose of machine learning algorithms is to design computer tools that can effectively find the inherent relations between the inputs and outputs of a given complex system, and subsequently predicting the desired unknown data (e.g., the presence or absence of a critical crack in the current state of a structure) or judging its characteristics (e.g., the crack length). Generalization and robustness of the learning algorithms are vital to SHM system designers and require the ability of a chosen algorithm to predict the structure’s response when confronted with input data outside the nominal training set (i.e., the problem of uncertainty) [5] .
To elaborate on the latter concept of uncertainty, let us consider a sample SHM framework shown in Figure 1. The uncertainty in this system may come from the sensing systems by means of inaccurate data transmitted from sensors or imprecise database developed during the damage signature development process, manufacturing errors, environmental noises, loading perturbations, or the feature extraction/classification toolboxes; all of which can be potentially misleading for the SHM alerts or result in imprecise predictions [2] . Thus, performance and robustness of the SHM system in high-risk applications, such as those in aerospace, should be examined in the presence of noise and uncertainty of input parameters. Such type of SHM uncertainty has been exemplified earlier via a numerical case study [5] on a composite T-joint [6] , which suggested that “the variation caused in the response of the structure due to uncertainty sources could be as large as those by the damage it self”, hence a clear need for developing more robust SHM systems.
As a step forward to address the above need, the main aim of this article is to conduct an investigation into the development of a robust SHM via a weighted Artificial Neural Network (ANN), which can be immune against potential manufacturing errors in the structure. The selected case study is on predicting the location and extent of delamination in a composite airfoil [5] with the NACA-0012 profile under tensile loading [6] . Section 2 describes the experimental setup of the airfoil, the finite element model of the structure, and the developed damage signature database (DSD) to train the SHM. Section 3 provides background information on defining the proposed robust ANN SHM of the airfoil, based on a concept of signal-to-noise (SN) weighting. Section 4 provides the analysis results from the DSD along with an ANOVA analysis for correlating strain responses to the pre-def- ined damage scenarios, and thereby to quantify the significance of SHM uncertainty parameters. The same section follows with results of different weighted and unweighted ANNs, designed to predict damage in the structure from strain signatures in the presence of manufacturing errors (here in the form of composite ply thickness variations). Finally, Section 5 summarizes the main findings of the study and outlines some practical notions regarding the implementation of the proposed SN-ANN SHM.
Figure 1. Example of a SHM system with different features [2] .
2. Case Study Description
The selected composite NACA-0012 airfoil is a sandwich structure consists of a 3 mm thick PVC foam, reinforced with E-glass and carbon woven fabrics (Figure 2). Table 1 lists the stacking sequence of the laminate schedule. A prototype structure was manufactured using the hand layup process and elastic material properties of the laminate components were estimated based on earlier studies [7] -[9] (Table 2).
Figure 2. The NACA0012 composite airfoil lay-up used in the case study.
Table 1. Stacking sequence of the airfoil and nominal ply thicknesses.
Table 2. The material properties used for modeling the airfoil plies (x-index refers to the fiber direction; woven fabrics in FE simulations were modeled as a cross-ply laminate).
The airfoil profile was initially tested under a pre-defined set of delamination scenarios under static tensile loading (Figure 3). Subsequently, a finite element (FE) model of the set-up with the material data in Table 2 was established in Abaqus/Standard and validated against experimental data. More details of the tensile experiments and the Finite Element verification can be found in [10] . The numerical model was employed as a virtual experimental tool to create more damage scenarios with varying ply thicknesses (mimicking a typical type of manufacturing error). Overall 166 damage scenarios were developed considering delaminations with different lengths, ranging from 1.5 cm to 4.5 cm, and at different locations along the chord line of the airfoil between the lower carbon ply and the middle PVC foam of the NACA0012 airfoil, with the internal chord of 31 cm and the external chord of 33.5 cm. Figure 4(a), Figure 4(b) illustrate a general scheme of the delaminations of different lengths and locations as used in establishing the damage signature database (DSD). It is noted that in each individual damaged airfoil scenario in the DSD, one single delamination (i.e., one size, one location) was implemented. It is also noted that 17 positions along the lower surface of the airfoil were considered as sensory points to estimate an accurate (semi-continuous) strain distribution in each DSD simulation.
To account for manufacturing uncertainty, ply thickness variations due to the hand layup production process were assumed to change from one sample to another. The thickness variation range was initially estimated based on tensile experiments. Namely, Table 3 shows the global displacement variations observed at different loading values for the tested airfoils with no delamination. It was assumed that these variations in the structure’s global response have been equivalently caused by variations in thickness of different plies (carbon 200 gr/m3 and glass 200 gr/m3; both below and above the PVC foam). Subsequently, the FE model was used along with an inverse method to determine a reasonable thickness variation range for each of the above mentioned plies to cover at least 60% of experimental data scatter. The obtained lower and upper thickness limits (Table 4), which were also common during the hand laid-up trials, were next employed to generate random values in the subsequent stochastic simulations for each ply thicknesses, assuming a uniform probability density function. In summary, each damage scenario was simulated with five randomly varying ply thicknesses, in addition to the nominal thickness case listed in Table 1. Next, the goal was to employ the simulated DSD and develop a robust SHM to predict both damage size and location in the airfoil.
3. Signal-to-Noise Weighted Artificial Neural Network Development
The Artificial Neural Networks (ANNs) are known as crude electronic models that have been inspired by neural structure of the brain. According to Gurney [11] , ANNs “are interconnected assemblies of simple processing elements, units or nodes whose functionality is loosely based on the animal neuron. The processing ability of the network is stored in the inter-unit connection strengths, or weights, obtained by a process of adaption to, or learning from, a set of training patterns”. The classical machine learning theory is classified into three main categories: classification, regression, and density estimation [12] . The ANNs under the classification category have been widely used in SHM features such as structural load monitoring, usage prediction, and damage diagnostics [13] -[19] . Given an SHM application, different ANN architectures can be defined and optimized based on feed-forward and recurrent networks. The majority of the published work on the development of ANN SHMs has implemented feed-forward networks, and in particular the Multilayer Perceptron (MLP) networks [20] . There are limited reports, however, describing the application of recurrent networks, especially for NDT testing, SHM and material property characterization in general.
The input layer of a MLP network can receive, for instance, the strain measurements at different sensory point
Figure 3. A composite airfoil sample under tension [10] .
Figure 4. Sample delaminations with different lengths plotted adjacent to the PVC foam in the finite element model of the airfoil: (a) ~1 cm delamination, (b) ~2 cm delamination.
Table 3. Variation of displacement observed at different load magnitudes for different samples through repeats of the tensile tests [10] .
Table 4. Half of the calculated thickness ranges (in mm) of different composite layers to cover about 60% of the variation observed in the experiments [10] .
of the structure, and the output layer would predict the location and extent of the existing damage corresponding to the measured input data. As will be shown in Section 4, a conventional MLP ANN can be potentially unable to provide accurate results when optimally trained with un-noisy damage scenarios (i.e., here based on nominal computer simulations), and asked to predict the damage status in practice in the presence of uncertainties. For this reason, in the present work an application of the Signal-to-Noise (SN) ratio coefficients is tested to weigh the input layer of the MLP network (Figure 5) and possibly improve the accuracy of damage predictions.
Signal-to-noise ratio analysis is a means for comparing the level (amplitude) of a desired signal (target value) to the corresponding level of background noise (fluctuations/variation) in measurements. This concept has been widely used in electrical and electromagnetics engineering where the log function of the ratio of signal to noise is defined as the SN factor. In general, there are four types of SN’s [21] :
Lower-the-better static SN: 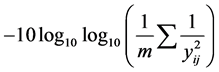 also called SN-L;
also called SN-L;
Higher-the-better static SN: 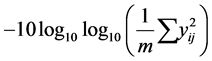 also called SN-H;
also called SN-H;
Nominal-the-best static SN: 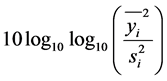 where
where 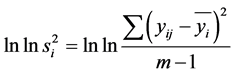 also called SN-M.
also called SN-M.
Here for a given sensor on the structure, 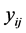 is defined as the sensor reading in the ith damage scenario and the jth thickness variation (test repeat). In another type of so-called ‘dynamic’ signal-to-noise ratio analysis, for each sensor point all the measured data are plotted in the ordered x-y plane (here damage scenario versus measurements) and the slope of a regression line passing through them is calculated (see [21] for theoretical details). If MSE indicates the mean square error of sample measurements, the dynamic SN ratio is then defined as:
is defined as the sensor reading in the ith damage scenario and the jth thickness variation (test repeat). In another type of so-called ‘dynamic’ signal-to-noise ratio analysis, for each sensor point all the measured data are plotted in the ordered x-y plane (here damage scenario versus measurements) and the slope of a regression line passing through them is calculated (see [21] for theoretical details). If MSE indicates the mean square error of sample measurements, the dynamic SN ratio is then defined as:
Zero-proportional Dynamic SN: 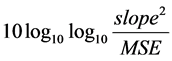 also called SN-D.
also called SN-D.
For the present study, only the SN-M and SN-D methods are physically meaningful as the sensor values under each damage condition are always best if they are nominal (not the lower the better, not the higher the better). It is to note that in comparison with the SN-M mode, in the dynamic mode SN-D, the measurement values are not averaged (assumed constant) over the entire damage scenarios; instead it is assumed that the nominal value of measurements at each sensor point can vary with the damage scenario. As a result, it is expected that the SN-D method outperforms the SN-M method in such SHM applications (more on this topic to follow in the next section). Table 5 lists these SN ratios for the DSD of the composite airfoil. In fact, the obtained SN coefficients are
Figure 5. Schamtic of a multilayer perceptron ANN (adapted from [33] ), weighted by the proposed S/N ratios at the input layer.
Table 5. Summary of obtained signal-to-noise (SN) ratios.
expressing the vulnerability of each individual sensory point under the simultaneous presence of damage and thickness variation scenarios. Regardless of the type, a higher SN coefficient indicates a stronger average signal compared to the noise level, which implies the robustness of the corresponding sensor in reporting the abnormalities caused by the damage status.
Examples of the application of the concept of signal-to-noise ratio in other engineering and medical applications include the quantification of noise in MRI (Magnetic Resonance Imaging) systems [22] , diffusion weig- hted images of spinal cords [23] , electrocardiograms [24] , ultrasonic non-destructive testing of highly scattering materials [25] , etc. The idea of weighting the input layer of a neural network to demonstrate the importance of individual measurement points has also been the topic of some past studies. Zou et al. [26] used back-propag- ation neural networks with a Levenberg-Marquardt learning algorithm to study the protein combinations of both amino acid and amino pairs. The overall accuracy of prediction reached 88.4%, which was a notable enhancement compared to the conventional neural network with an accuracy as low as 66.1%. Chen et al. [27] applied the weighted input layer (adapted from the information entropy theory) to the Elman NN to predict gas turbines performance. The application of the entropy theory to the conventional network resulted in a decreased mean square error of the training/prediction process by about 29%, for real-time predictions.
4. Damage Prediction Results and Discussion
The developed DSD in Section 2 was used in this section for two complementary analyses. First, an ANOVA analysis was established where the statistical significance of the uncertainty factors on the airfoil SHM predictions was proven statistically. Next, a series of Artificial Neural Network (ANN) SHMs were trained and compared for their prediction quality on the damage location and size, under the presence of manufacturing uncertainty factor and using the analytical framework presented in Section 3.
4.1. ANOVA Analysis
Table 5 shows the summary of ANOVA analysis of all 17 sensors in Figure 4, after running the FE model for the entire (166) scenarios of the damage signature database (DSD). The resulting p-values in Table 6 show that no sensor is able to merely focus on predicting the damage status, as all sensor values have been affected by the uncertainty factor (noise) with a P-value < 5%. An earlier statistical study [10] , which was based on the same numerical data but using only 3 instead of 166 damage scenarios, had concluded that among the distributed sensors, four sensor locations showed significantly higher sensitivities (i.e., P-values < 5%) to the damage factor than the thickness variation (noise). Hence, one would mistakenly conclude that those few sensor locations may be chosen for the subsequent DSD training purposes during robust SHM development. However, as seen in Table 6, when a large damage database used (here 166 scenarios), in fact all sensors can be significantly affected by the noise against prediction of damage at different locations and with different sizes. Hence, two conclusions may be made here when comparing the present ANOVA results and those of [10] :
First, it is critical to ensure that a given DSD contains sufficient number of damage scenarios to accurately represent the reality.
Second, for a sufficiently large damage database, and with uncertainty propagated throughout the structure, caution must be taken not to pre-define/prefer limited sensor locations to be used for training proposes.
Table 6. ANOVA analyses for 166 damage scenarios under uncertainty factor (note that a P-value of nearly zero indicates a very high statistical significance/sensitivity).
4.2. Weighted and Unweighted MLP ANN’s
As addressed in Section 3, MLP Artificial Neural Networks are powerful techniques used for pattern recognition purposes in SHM applications [28] -[33] . ANNs are provided with the measured sensory information such as displacement, acceleration, stress/strain, damping ratio, and mode shapes, in time or frequency domains, and are expected to correlate these data to the state of damage (location and size of defect) in the structure.
In the current example, the well-known technique of k-fold cross validation [33] was used to arrive at architecturally optimized ANN architectures. This technique helps the analyst select the number of hidden layers, number of neurons in each hidden layer, activation function, learning algorithm and learning rule. This was initially done for the airfoil’s SHM using the nominal DSD only (i.e., without considering noise). The summary of the obtained cross validation results for the nominal damage cases are presented in Table 7. During the cross- validation, in each iteration 70% of the dataset was considered to be the training set and the 30% for validation and testing; i.e. for instance when the network was optimized on the original 166 dataset, 116 sets were used for training and 50 sets for validation and testing. The best trained network for this SHM had 17 neurons in the first layer (input layer), 24 neurons in the second layer, 20 neurons in the third layer, 8 neurons in the fourth layer and 2 neurons in the last layer (also known as output layer). This network (24-20-8-2 NN in Table 7) was then used to predict damage in all simulated airfoils, both with and without uncertainty (i.e., versus the total DSD). In addition, for comparison purposes, the same network was trained with both nominal and noisy damage scenarios and again used to predict the total DSD. Results of the aforementioned approaches are provided in Table 8.
Concerning the low prediction% values in Table 8, it is clear that the conventional (unweighted) ANN has not been capable of predicting the thickness varying scenarios when it is only trained by the nominal DSD. When the same network is trained with the total DSD, however, it has greatly become capable of predicting
Table 7. Optimized neural networks for the nominal DSD without thickness variation.
Table 8. Comparison of the neural networks for nominal and thickness varying damage scenarios.
damage location (97.0%) and damage extent (95.8%) under uncertain input data. This shows a desirable generalizability of the ANN for robust SHM applications, but it can also pose an important challenge. Namely, in practice the second unweighted but robust ANN will require testing all damage scenarios under several random repeats to arrive at a sufficiently large DSD to be included in the training pool. Running such large DSDs with several noise scenarios would normally pose high cost and time limitations in industrial settings.
To address this challenge, we next attempted to use SN ratios to weigh the input layer of the MLP ANN. Table 8 illustrates the prediction results where the conventional neural network has been weighted by the SN ratios of Table 5 and predicted the noisy (total) DSD. Note that the noisy DSD scenarios have not been directly used in the latter training process, but their impacts have been condensed in the SN ratios. Both the SN-M and SN-D weighting methods have resulted in an improved performance of SHM when used on the original optimum ANN architecture with or without re-optimization. By implementing the “dynamic” signal to noise ratio (SN-D), how- ever, the accuracy of damage location prediction was found to be the highest among all tested ANN models (as high as ~92%).
5. Concluding Remarks
MLP Artificial Neural Networks have proven to be powerful tools for pattern recognition in the structural health monitoring applications, yet its efficiency can reduce when dealing with unseen uncertainty in the input layers of a system such as ply thickness variation in the composite laminate. Using a case study on a composite airfoil and ANOVA analysis over a DSD with 166 damage scenarios along with five random repeats of each due to manufacturing error, it was found that all the sensory points exhibited almost the same delamination detection sensitivity as the uncertainty effect itself, hence the clear need for a robust SHM development. Also by comparing the above results to the earlier study [10] , it was found that the small-size DSDs could be misleading in terms of preselecting specific sensory points to be immune against noise, especially when the uncertainty had been propagated throughout the structure.
One way to deal with uncertainty in the input of SHM data is to include the uncertainty scenarios in the training set, but this approach would involve developing a vast damage database which often requires considerable time and budget for industries. Another approach discussed here would be weighing the conventional neural network by signal-to-noise coefficients. In the performed case study, the noisy DSD was analyzed for each input neuron to calculate an appropriate SN ratio. The approach dramatically increased the efficiency of the ANN- based SHM, even though it was only trained with the original damage scenarios (nominal DSD) and predicted the noisy DSD. Table 8 is a complete summary of all different training and prediction scenarios using the unweighted ANN and weighted ANNs. Among different types of SN, the dynamic SN weighted neural network showed a superior accuracy above 90% in damage prediction. A practical problem with this approach, however, is the reliable estimation of SN weights. This estimation may come from past experience, expert knowledge or by developing a sub-set of initial DSD encompassing uncertainty cases.
This project is a part of a larger research program aiming at identifying practically and economically most viable, yet accurate and robust, algorithms for implementation in real-time SHM systems of composite structures. The assessment of other powerful non-parametric methods such as the Gaussian Processes (GPs) is also of high interest in developing and comparing future robust SHMs.
Acknowledgements
This research was funded by the Natural Science and Engineering Research Council of Canada (NSERC), under the Discovery Grants Program.
Cite this paper
HessamodinTeimouri,Abbas S.Milani,RudolfSeethaler,AmirHeidarzadeh, (2016) On the Impact of Manufacturing Uncertainty in Structural Health Monitoring of Composite Structures: A Signal to Noise Weighted Neural Network Process. Open Journal of Composite Materials,06,28-39. doi: 10.4236/ojcm.2016.61004
References
- 1. Boller, C. and Meyendorf, N. (2008) State-of-the-Art in Structural Health Monitoring for Aeronautics. Proceedings of International Symposium on NDT in Aerospace, Fürth/Bavaria, Germany, 3-5 December 2008.
- 2. Balageas, D., Fritzen, C.P. and Gumes, A. (2006) Structural Health Monitoring. Antony Rowe Ltd., Chippenham, Wiltshire.
- 3. Perez, I., DiUlio, M., Maley, S. and Phan, N. (2010) Structural Health Monitoring in the Navy. International Journal of Structural Health Monitoring, 9, 199-209. http://dx.doi.org/10.1177/1475921710366498
- 4. Lopez-Higuera, J.M. (2002) Introduction to Optical Fiber Sensor Technology. In: Lopez-Higuera, J.M., Ed., Handbook of Optical Fibre Sensing Technology, Wiley, New York, 1-21.
- 5. Teimouri, H., Milani, A.S. and Seethaler, R. (2013) On the Effect of Fabrication and Testing Uncertainties in Structural Health Monitoring. In: Silva, M., Ed., Design of Experiments Applications, InTech, Croatia. http://dx.doi.org/10.5772/56530
- 6. Kesavan, A., John, S. and Herszberg, I. (2008) Strain Based Structural Health Monitoring of Complex Composite Structures. Structural Health Monitoring, 7, 1-13.
- 7. Kachlakev, D.I. (1998) Finite Element Method (FEM) Modeling for Composite Strengthening/Retrofit of Bridges. Research Project Work Plan, Civil, Construction and Environmental Engineering Department, Oregon State University, Corvallis, Oregon.
- 8. Kachlakev, D.I. (1998) Strengthening Bridges Using Composite Materials. FHWA-OR-RD-98-08, Oregon Department of Transportation, Salem, Oregon.
- 9. Kachlakev, D.I. and McCurry Jr., D. (2000) Simulated Full Scale Testing of Reinforced Concrete Beams Strengthened with FRP Composites: Experimental Results and Design Model Verification. Oregon Department of Transportation, Salem, Oregon.
- 10. Teimouri, H., Milani, A.S., Seethaler, R., Abedian, A., Heidarzadeh, A. and Teimouri, B. (2013) Towards Strain-Based Structural Health Monitoring of Composite Airfoil under Uncertainty. 19th International Conference on Composite Materials, Montreal, Canada, July-August 2013, 1-8.
- 11. Gurney. K. (1997) An Introduction to Neural Networks. University of Sheffield, UK. http://dx.doi.org/10.4324/9780203451519
- 12. Chu, F., Yuan, S. and Peng, Z. (2009) Machine Learning Techniques. Encyclopedia of Structural Health Monitoring.
- 13. Azzam, H. (1997) A Practical Approach for the Indirect Prediction of Structural Fatigue from Measured Flight Parameters. Proceeding of the Institution of Mechanical Engineering, Part G: Journal of Aerospace Engineering, 211, 29-38. http://dx.doi.org/10.1243/0954410971532479
- 14. Azzam, H. (1997) The Use of Mathematical Models and Artificial Intelligent Techniques to improve Hums Prediction Capabilities. Proceedings of the Royal Aeronautical Society, Innovation in Rotorcraft Technology Conference, London, 24-25 June 1997, 16.1-16.14.
- 15. Azzam, H., Hebden, I., Gill, M., Beavan, F. and Wallace, M. (2005) Fusion and Decision Making Techniques for Structural Prognosis Health Management. IEEE Aerospace Conference, Montana, MT, 5-12 March 2005, Paper #1535.
- 16. Wallace, M., Azzam, H. and Newman, S. (2004) Indirect Approaches to Individual Aircraft Structural Monitoring. Proceeding of the Institution of Mechanical Engineering, Part G: Journal of Aerospace Engineering, 218, 329-346. http://dx.doi.org/10.1243/0954410042467059
- 17. Reed, S.C. and Cole, D.G. (2003) Development of a Parametric Aircraft Fatigue Monitoring System Using Artificial Neural Network. Proceedings of the 22nd Symposium of the International Committee on Aeronautical Fatigue, Lucern, 9 May 2003, 47-63.
- 18. Scallonila, G., Cracia, J., Cabrejas, J. and Armijo, J.I. (2007) A Full-Scale Parametric Based Fatigue Monitoring System Using Neural Networks. Proceedings of the 24th Symposium of the International Committee on Aeronautical Fatigue, Naples, 16-18 May 2007.
- 19. Levinski, O. (2001) Australian Defense Science and Technology Organization. Prediction of Buffet Loads Using Artificial Neural Network, Document DSTO-RR-0218.
- 20. Teimouri, H. (2015) A New Statistical Approach to Strain-Based Structural Health Monitoring of Composites under Uncertainty. PhD Dissertation in Mechanical Engineering, University of British Columbia, BC, Canada.
- 21. Fowlkes, W.Y. and Creveling, C.M. (2013) Engineering Methods for Robust Product Design: Using Taguchi Methods in Technology and Product Development. Prentice Hall, Englewood Cliffs.
- 22. Welvaert, M. and Rosseel, Y. (2013) On the Definition of Signal-to-Noise Ratio and Contrast-to-Noise Ratio for fMRI Data. PLoS ONE, 8, e77089. http://dx.doi.org/10.1371/journal.pone.0077089
- 23. Griffantia, L., Baglioa, F., Pretia, M.G., Cecconic, P., Rovarisd, M., Basellib, G. and Laganà, M.M. (2012) Signal-to- Noise Ratio of Diffusion Weighted Magnetic Resonance Imaging: Estimation Methods and in Vivo Application to Spinal Cord. Biomedical Signal Processing and Control, 7, 285-294. http://dx.doi.org/10.1016/j.bspc.2011.06.003
- 24. Poungponsri, S. and Yu, X.H. (2013) An Adaptive Filtering Approach for Electrocardiogram (ECG) Signal Noise Reduction Using Neural Networks. Neurocomputing, 117, 206-213. http://dx.doi.org/10.1016/j.neucom.2013.02.010
- 25. Liu, A., Lu, M. and Wei, M. (1997) Structure Noise Reduction of Ultrasonic Signals Using Artificial Neural Network Adaptive Filtering. Ultrasonics, 35, 325-328. http://dx.doi.org/10.1016/S0041-624X(97)00009-7
- 26. Zou, L., Wang, Z. and Huang, J. (2007) Prediction of Subcellular Localization of Eukaryotic Proteins Using Position- Specific Profiles and Neural Network with Weighted Inputs. Journal of Genetics and Genomics, 34, 1080-1087. http://dx.doi.org/10.1016/S1673-8527(07)60123-4
- 27. Chen, T., Xu, X. and Wang, S. (2011) An Intelligent Prediction Method Based on Information Entropy Weighted Elman Neural Network. Proceedings of the Intelligent Computing and Information Science: International Conference, Chongqing, 8-9 January 2011, Part II, 142-147. http://dx.doi.org/10.1007/978-3-642-18134-4_23
- 28. Fang, X., Luo, H. and Tang, J. (2005) Structural Damage Detection Using Neural Network with Learning Rate Improvement. Computers and Structures, 83, 2150-2161. http://dx.doi.org/10.1016/j.compstruc.2005.02.029
- 29. Kesavan, A., John, A. and Herszberg, I. (2008) Strain-Based Structural Health Monitoring of Complex Composite Structures. Structural Health Monitoring, 7, 203-213. http://dx.doi.org/10.1177/1475921708090559
- 30. Al-Haik, M.S., Hussaini, M.Y. and Garmestani, M. (2006) Prediction of Nonlinear Viscoelastic Behaviour of Polymeric Composites Using an Artificial Neural Network. International Journal of Plasticity, 22, 1367-1392. http://dx.doi.org/10.1016/j.ijplas.2005.09.002
- 31. Koker, R., Altinkok, N. and Demir, A. (2006) Neural Network Based Prediction of Mechanical Properties of Particulate Reinforced Metal Matrix Composites Using Various Training Algorithms. Materials & Design, 28, 616-627.
- 32. Singh, A.P., Kamal, T.S. and Kumar, S. (2005) Virtual Curve Tracer for Estimation of Static Response Characteristics of Transducers. Measurement, 38, 166-175. http://dx.doi.org/10.1016/j.measurement.2005.04.005
- 33. Haykin, S. (1997) Neural Networks—A Comprehensive Foundation. 2nd Edition, Prentice-Hall Inc., Upper Saddle River.








