Journal of Power and Energy Engineering
Vol.06 No.11(2018), Article ID:88741,13 pages
10.4236/jpee.2018.611004
Stabilization of Wind Farm by Using PMSG Based Wind Generator Taking Grid Codes into Consideration
Md. Rifat Hazari1*#, Mohammad Abdul Mannan2, Atsushi Umemura1, Rion Takahashi1, Junji Tamura1
1Department of Electrical and Electronic Engineering, Kitami Institute of Technology (KIT), 165 Koen-cho, Kitami, Hokkaido 090-8507, Japan
2Department of Electrical and Electronic Engineering, American International University-Bangladesh (AIUB), 408/1, Kuratoli, Khilkhet, Dhaka, Bangladesh

Copyright © 2018 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: October 25, 2018; Accepted: November 23, 2018; Published: November 26, 2018
ABSTRACT
This paper presents a new operational strategy for a large-scale wind farm (WF) which is composed of both fixed speed wind turbines with squirrel cage induction generators (FSWT-SCIGs) and variable speed wind turbines with permanent magnet synchronous generators (VSWT-PMSGs). FSWT-SCIGs suffer greatly from meeting the requirements of fault ride through (FRT), because they are largely dependent on reactive power. Integration of flexible ac transmission system (FACTS) devices is a solution to overcome that problem, though it definitely increases the overall cost. Therefore, in this paper, a new method is proposed to stabilize FSWT-SCIGs by using VSWT-PMSGs in a WF. This is achieved by injecting the reactive power to the grid during fault condition by controlling the grid side converter (GSC) of PMSG. The conventional proportional-integral (PI)-based cascaded controller is usually used for GSC which can inject small amount of reactive power during fault period. Thus, it cannot stabilize larger rating of SCIG. In this paper, a suitable fuzzy logic controller (FLC) is proposed in the cascaded controller of GSC of PMSG in order to increase reactive power injection and thus improve the FRT capability of WF during voltage dip situation due to severe network fault. To evaluate the proposed controller performance, simulation analyses are performed on a modified IEEE nine-bus system. Simulation results clearly show that the proposed method can be a cost-effective solution which can effectively stabilize the larger rating of SCIG compared to conventional PI based control strategy.
Keywords:
Wind Turbine Generator, Fuzzy Logic Controller, Power System Stability, Power Converter, PI Controller

1. Introduction
Global warming is one of the serious problems that the world faces recently due to the use of fossil fuel-based power plants to generate electricity [1] . Owing to the drawbacks of conventional power plants, clean energy has grown significantly since the last decade. Wind power (WP) is one of the clean energy sources which grow significantly since the last decade. According to the global wind energy council (GWEC), the cumulative installation size of WP was 539.1 GW at the end of 2017 and it will reach 840.9 GW by 2022 [2] . This huge installation of WP into the power system has serious impacts on system stability. In order to continue the smooth operation of power grid including WP, FRT necessities have been executed all over the world. It demands that the WF must remain connected to the power grid during a fault event and support the system in a similar way as conventional synchronous generators (SGs) [3] .
Most of the WFs are constructed using FSWT-SCIG due to their superior characteristics, e.g., brushless operation, robust construction, operational simplicity and low cost [4] . However, the SCIG is directly coupled with the grid system and does not have FRT capability during network disturbance situation [4] . In addition, the SCIG necessitates large reactive power during fault situations to recover air gap flux. If sufficient reactive power is not injected, the developed electromagnetic torque drops significantly. Usually, a capacitor bank is placed near the SCIG terminal to inject the reactive power. However, the SCIG requires large amount of reactive power during transient period than steady state condition and the capacitor bank is unable to inject this high amount of reactive power during transient period.
In order to improve the FRT capability during network fault situation, some supplementary devices, for example, an energy capacitor system (ECS) [5] , superconducting magnetic energy storage (SMES) [6] , and a static synchronous compensator (STATCOM) [7] are installed in WFs with FSWT-SCIGs. However, the overall system cost increases.
On the other hand, the VSWT-PMSG is a smart kind of wind turbine system in which both active and reactive power output can be controlled effectively [8] . The advantages of VSWT-PMSG configurations are [9] [10] : 1) No brushes and gearbox, thus higher reliability and lower maintenance are required; 2) The full power converter totally decouples the generator from the grid, therefore power system disturbances have no direct impact on the generator; 3) No supplementary power supply for magnetic field excitation is required as permanent magnet is used in the rotor; 4) The converter allows very flexible control of active and reactive power in all grid conditions (normal or disturbed); 5) The converter can fully control the amplitude and frequency of the generator voltage. However, the only drawbacks of VSWT-PMSG are expensive cost due to use of full rating power electronic AC/DC/AC converter. Thus, combined installation of small-scale VSWT-PMSG along with large-scale FSWT-SCIG could be an effective solution. The VSWT-PMSG system can supply additional amount of reactive power during transient period to the FSWT-SCIG. Therefore, the FRT capability of SCIG can be ensured at lower cost. The power converters of PMSG consist of machine side converter (MSC) and GSC. The GSC is responsible to inject reactive power to the grid system [11] . Thus, the designing of GSC control strategy is very crucial and equally important. Normally, cascaded control strategy based on four conventional PI controllers is used in the inner and outer loops of GSC controller [11] . But the accomplishment of the conventional PI controller is insufficient during transient period and it cannot provide effective amount of reactive power [12] . This is because, for example, conventional PI controller cannot deal with the system non-linearity due to parameter changes in the grid system. According to the deviation of the grid system impedances, gain margin and phase margin of the control system should be changed.
On the other hand, the FLC can handle nonlinear systems very effectively because it offers variable gain during transient conditions. Compared with conventional PI controller, FLC has the potential to provide an improved method even in the wide parameter variations. The FLC can take the place of conventional PI controller.
Thus, using an FLC in the inner loop of GSC controller to provide efficient amount of reactive power to stabilize SCIG-based WF during fault periods is convenient. Therefore, the main contribution of this paper is the design of a novel FLC-based GSC controller of PMSG to improve the FRT capability and stabilize the gird-connected SCIG-based WF. Detailed design procedure and control strategies of the overall system are presented in this paper. The effectiveness of the proposed control strategy is verified by both transient and dynamic simulation analyses. Real wind speed data measured in Hokkaido Island, Japan, are used for dynamic study.
The transient performance of the overall system composed of proposed GSC controller controlled PMSG, SCIG, and conventional SGs is compared with that composed of a PMSG controlled by conventional PI-based cascaded controller presented in [11] . Finally, it is found that the proposed FLC-based GSC controller is very effective to improve the FRT capability of SCIG-based WF.
The rest of the paper is organized as follows. Section 2 presents the description of power system model. Section 3 describes the wind turbine model, and the design procedure of the PMSG control system with proposed GSC controller is introduced in Section 4. The simulation results and a discussion of the performance of the proposed and conventional methods are presented in Section 5. Finally, Section 6 summarizes the findings and concludes the paper.
2. Description of Power System Model
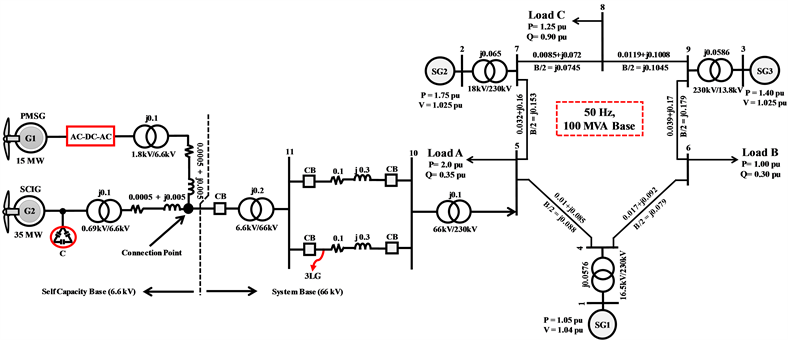
This study employed the power system model illustrated in Figure 1 for transient stability and dynamic performance analyses. It is composed of IEEE nine-bus main model and a WF. The main system consists of three conventional SGs (SG1 rating: 150 MVA, SG2 rating: 250 MVA and SG3 rating: 200 MVA). IEEE type AC4A exciter model presented in [13] is considered for all SGs. The SG1 and SG2 are thermal power plants whereas SG3 is a hydro power plant. The models and parameters of thermal and hydro governor systems are taken from [13] . The WF is connected to bus 5 through double circuit transmission lines, transformers, and it consists of one SCIG (rated capacity: 35 MW) and one PMSG (rated capacity: 15 MW) as shown in Figure 1. The total capacity of WF is 50 MW. Each PMSG and SCIG are denoted by an aggregated equivalent single generator to decrease computational time [14] [15] . The parameters of conventional SGs, SCIG, and PMSG are presented in Appendix.
3. Wind Turbine Model
The extracted mechanical power from a wind turbine can be expressed as [8] :
(1)
where,
(2)
(3)
(4)
where, Pw = Captured wind power, ρ = Air density (KG/m3), R = Radius of the
Figure 1. Power system model.
rotor blade (m), Vw = Wind speed (m/s), Cp = Power coefficient, β = Pitch angle,and λ = Tip speed ratio. In addition, c1 to c6 are characteristic coefficients of wind turbine [16] , and ωr = rotational speed of wind turbine (rad/s).
The maximum power point tracking (MPPT) technique shown in Equation (5) is adopted in this work [8] .
(5)
The rotating mass of variable speed wind turbine is composed of rotor hub with blades and generator shaft. The two-mass drive train model is considered in this work [11] [17] .
4. PMSG Model and Control System
An arrangement of VSWT-PMSG and control scheme is illustrated in Figure 2. The complete system comprises wind turbine with drive train models, PMSG without gearbox, MSC, GSC, and pitch angle controller. The both converters are built by using two levels of insulated gate bipolar transistor (IGBT), and the machine side controller and the grid side controller are responsible for controlling them. The MSC is directly associated to the stator terminal of PMSG whereas the GSC is attached to the grid system through step up transformers. PMSG model available in PSCAD library is used in this work [18] . A DC chopper is located in the DC-Link circuit. It is controlled by the comparator block. When the DC-link voltage (Vdc) ≥ 1.05 pu, the comparator activates the DC chopper and protect the DC-Link circuit. The pulse width modulation (PWM) method is used in this work and the carrier frequency is taken 3.0 kHz for both converters. The rated Vdc is 3.0 kV.
4.1. Machine Side Controller
The MSC transforms the three phase AC voltage generated by PMSG to DC voltage. The controller for MSC is composed of four conventional PI controllers as depicted in Figure 3. The controller is consisting of two loops; upper loop is for
Figure 2. Arrangement of PMSG system.
Figure 3. Machine side controller.
reactive power whereas lower one is for active power. The q-axis current (Isq) and the d-axis (Isd) current control the active power (Ps) and reactive power (Qs) of the PMSG system, respectively. The reference active power (Pref) is obtained by the MPPT algorithm described in Section 3. The unity power factor operation is performed by setting the reference reactive power ( ) to zero.
4.2. Grid Side Controller
This chapter describes the proposed controller of GSC and detail design procedure of FLC.
4.2.1. Proposed Grid Side Controller Operation
The GSC transforms the DC voltage into three phase AC voltage of the grid frequency. Figure 4 depicts the proposed controller for GSC. It is composed of three PI controllers and one FLC. The controller is used to control the reactive power (Qg) delivered to the grid and keep the Vdc constant by using the d-axis (Igd) and q-axis (Igq) currents of GSC. The FLC is used in the inner loop of the GSC controller to supply reactive power more efficiently during fault condition. Based on the system parameters, the FLC can provide variable gain. Therefore, it is possible to inject effective amount of reactive power during transient period. Thus, the terminal voltage can quickly be going back to the pre-fault value. In addition, the proposed control strategy can effectively stabilize the SCIG-based WF compared to conventional PI based cascaded GSC controller of PMSG.
4.2.2. Fuzzy Logic Controller Design
In order to design the proposed FLC, the error of the grid d-axis current (eIgd) and rate of change of the eIgd (ceIgd) are considered as the controller inputs. The grid d-axis voltage reference ( ) is chosen as the controller output. The main structure of the FLC consists of fuzzification, rule base, fuzzy inference, and defuzzification as illustrated in Figure 5 [19] . For fuzzification, the triangular membership functions with overlap are used for inputs and output as shown in Figure 6, in which the linguistic variables NB, NM, NS, ZO, PS, PM, and PB stand for negative big, negative medium, negative small, zero, positive small,
Figure 4. Proposed grid side controller.
Figure 5. Structure of FLC.
Figure 6. Membership functions: (a) inputs (eIgd, ceIgd), and (b) output ( ).
positive medium, and positive big, respectively. The membership functions have been determined by trial and error approach to obtain the best system performance.
The rules of fuzzy mapping of the input variables to the output are specified in the form below:
IF
The entire rule base is presented in Table 1, which includes a total of 49 rules.
In this work, Mamdani’s max-min method is used as the inference mechanism [19] . For defuzzification, the center of gravity method is used in order to obtain [19] .
5. Simulation Results and Discussion
5.1. Transient Stability Analysis
In this study, simulations were conducted by using PSCAD/EMTDC software on
Table 1. Fuzzy rules.
the power system model illustrated in Figure 1. The FLC was designed using FORTRAN code. For transient stability analysis, three line to ground (3LG) fault near bus 11 was considered as depicted in Figure 1. The fault is considered to happen at 0.1 s, the duration of fault is 0.1 s (5 cycles), the circuit breakers (CBs) on the faulty line are opened at 0.2 s in order to isolate the faulty line from the entire power system and reclosed at 1.0 s. The simulation time is 10.0 s with a solution time step of 5 µs. The wind speed applied to each wind turbine is kept constant at 11.0 m/s based on the assumption that the wind speed does not change dramatically within this short period. Simulations were performed for two cases in order to validate the effectiveness of the proposed FLC controlled GSC controller of PMSG.
Case 1: with conventional cascaded GSC controller of PMSG presented in [11] .
Case 2: with proposed cascaded FLC-based GSC controller of PMSG presented in Section 4.2.
The grid code of FRT requirement for WF which is considered in this study is illustrated in Figure 7 [3] . Based on the curve, the wind turbine must stay connected with the power system if the voltage dip is within the defined range.
The simulation results of PMSG, SCIG, and SGs are depicted in Figure 8 and Figure 9, respectively. The reactive power injected by PMSG to the SCIG system in Case 2 is greater than that in Case 1 after a severe network fault as shown in Figure 8(a). Thus, the connection point voltage is recovered to the pre-fault value more quickly in Case 2 whereas it fails in Case 1 as depicted in Figure 8(b). Since the connection point voltage does not satisfy the standard FRT graph presented in Figure 7 for Case 1, the WF is disconnected from the power system by opening the CB near the connection point of wind generators at t = 2 s. Figure 8(c) shows the rotor speed response of SCIG. As the reactive power injection by PMSG is insufficient in Case 1, thus, the rotor speed of SCIG becomes unstable. On the other hand, the reactive power injection by PMSG is higher and more effective in Case 2, thus, the rotor speed becomes stable in this case. The DC-Link voltage is returned to the steady-state value more quickly in Case 2, wherein it failed to back to the steady-state value in Case 1 as shown in Figure 8(d).
Figure 7. FRT requirement for WF.
Figure 8. Responses of wind generators: (a) PMSG reactive power, (b) voltage at connection point of wind generators, (c) SCIG rotor speed, and (d) PMSG DC-Link voltage.
Figure 9. Responses of conventional SGs: (a) SGs rotor speed, and (b) SGs load angle.
Figure 9(a) and Figure 9(b) illustrate the rotor speed and power angle responses of conventional SGs (δSGs) with respect to SG1 load angle (δSG1). It is clearly seen from the figures that the rotor speed and power angle responses of SGs are more stable in Case 2 than Case 1. As a result, it can be concluded that the VSWT-PMSG with proposed FLC controlled GSC can enhance the transient stability of SGs as well as the voltage stability of the WF during transient condition.
5.2. Dynamic Performance Study
In this chapter, analysis about dynamic performance about the proposed GSC controller of PMSG is presented. The same power system model depicted in Figure 1 is used in this study. The total simulation time is 250.0 s. The real wind speed data measured at Hokkaido Island, Japan, shown in Figure 10(a), is used in the simulation. Figure 10(b) shows the reactive power output of each wind generator. The PMSG supplies the necessary reactive power to the SCIG for voltage regulation. Thus, the connection point voltage is approximately constant, as shown in Figure 10(c). Due to the fluctuations in the wind speed of wind generators, the frequency response of the power system is varying as shown in Figure 10(d). But, the frequency fluctuations lie within the permissible limit in Japan (±0.2 Hz).
The dynamic simulation study confirmed that the proposed FLC-controlled
Figure 10. Responses of power system: (a) applied wind speeds to wind generators, (b) reactive power output of wind generators, (c) voltage at connection point of wind generators, and (d) power system frequency response.
PMSG system can effectively supply reactive power and thus maintain the connection point voltage constant under a randomly varying wind speed.
6. Conclusions
This study proposes the application of fuzzy logic in GSC controller of PMSG to enhance the FRT capability of SCIG-based WF during transient period. The effectiveness of the proposed controller is tested by considering severe 3LG fault. The transient performance of the overall system composed of the proposed FLC-controlled PMSG, SCIG, and conventional SGs is compared with that of PMSG with the conventional control strategy. It is found that the proposed control strategy can ensure the FRT capability of WF as well as power system transient and steady-state stability. Therefore, it can be concluded that the proposed GSC controller for PMSG can be an effective solution to augment the transient stability of the grid-connected WF.
Application of adaptive neuro-fuzzy inference system (ANFIS) based control strategy of GSC for PMSG is strong candidate for future study.
Acknowledgements
This study was supported by the Grant-in-Aid for Scientific Research (B) from The Ministry of Education, Science, Sports and Culture of Japan.
Conflicts of Interest
The authors declare no conflicts of interest regarding the publication of this paper.
Cite this paper
Hazari, M.R., Mannan, M.A., Umemura, A., Takahashi, R. and Tamura, J. (2018) Stabilization of Wind Farm by Using PMSG Based Wind Generator Taking Grid Codes into Consideration. Journal of Power and Energy Engineering, 6, 40-52. https://doi.org/10.4236/jpee.2018.611004
References
- 1. Ula, A. (1991) Global Warming and Electric Power Generation: What Is the Connection? IEEE Transactions on Energy Conversion, 6, 599-604. https://doi.org/10.1109/60.103631
- 2. Global Wind Energy Council (GWEC) (2017) Annual Market Update 2017, Global Wind Report. http://www.gwec.net/
- 3. E. ON NETZ GmbH (2006) Grid Connection Regulation for High and Extra High Voltage. E. ON NETZ GmbH, Essen, Germany.
- 4. Muyeen, S.M., Mannan, M.A., Ali, M.H., Takahashi, R. and Tamura, J. (2006) Stabilization of Wind Turbine Generator System by STATCOM. IEEJ Transactions on Power and Energy, 126-B, 1073-1082.
- 5. Muyeen, S.M., Takahashi, R., Ali, M.H., Murata, T. and Tamura, J. (2008) Transient Stability Augmentation of Power Systems Including Wind Farms Using ECS. IEEE Transactions on Power Systems, 23, 1179-1187. https://doi.org/10.1109/TPWRS.2008.920082
- 6. Elshiekh, M.E., Mansour, D.A., Zhang, M., Yuan, W., Wang, H. and Xie, M. (2018) New Technique for Using SMES to Limit Fault Currents in Wind Farm Power Systems. IEEE Transactions on Applied Superconductivity, 28, 1-5.
- 7. Muyeen, S.M. (2015) A Combined Approach of Using an SDBR and a STATCOM to Enhance the Stability of a Wind Farm. IEEE Systems Journal, 9, 922-932. https://doi.org/10.1109/JSYST.2013.2297180
- 8. Muyeen, S.M., Tamura, J. and Murata, T. (2009) Stability Augmentation of a Grid Connected Wind Farm. Springer-Verlag, London.
- 9. Arani, M.F.M. and Mohamed, Y.A.I. (2016) Assessment and Enhancement of a Full-Scale PMSG-Based Wind Power Generator Performance under Faults. IEEE Transactions on Energy Conversion, 31, 728-739. https://doi.org/10.1109/TEC.2016.2526618
- 10. Zhao, Y., Qiao, W. and Qu, L. (2015) A Discrete-Time Direct Torque Control for Direct-Drive PMSG-Based Wind Energy Conversion Systems. IEEE Transactions on Industry Applications, 51, 3504-3514. https://doi.org/10.1109/TIA.2015.2413760
- 11. Rosyadi, M., Umemura, A., Takahashi, R., Tamura, J., Uchiyama, N. and Ide, K. (2015) Simplified Model of Variable Speed Wind Turbine Generator for Dynamic Simulation Analysis. IEEJ Transactions on Power and Energy, 135, 538-549.
- 12. Ferdi, B., Benachaiba, C., Dib, S. and Dehini, R. (2010) Adaptive PI Control of Dynamic Voltage Restorer Using Fuzzy Logic. Journal of Electrical Engineering: Theory and Application, 1, 165-173.
- 13. Kundur, P. (1994) Power System Stability & Control. McGraw-Hill Inc., 2 Pennsylvania Plaza New York City.
- 14. Ackerman, T. (2005) Wind Power in Power System. John Wiley & Sons, UK. https://doi.org/10.1002/0470012684
- 15. WECC Renewable Energy Modeling Task Force (2014) WECC Wind Power Plant Dynamic Modeling Guide.
- 16. Matlab Documentation Center (2018) http://www.mathworks.co.jp/jp/help/
- 17. Miller, N.W., Pric, W.W. and Samches-Gasca, J.J. (2003) Dynamic Modeling of GE 1.5 and 3.6 Wind Turbines-Generators. GE-Power System Energy Consulting.
- 18. PSCAD/EMTDC User’s Manual (1994) Manitoba HVDC Research Center, Canada.
- 19. Bose, B.K. (2001) Modern Power Electronics and AC Drives. Prentice Hall, PTR.
Appendix
The SGs, PMSG, SCIG, and drive train parameters used in this study are given in Table A1.
Table A1. Parameters of conventional SGs and wind generators.
NOTES