ABSTRACT

This article presents a comprehensive review for the dilemma of reactive power flow, while addressing different proposed remedy strategies: conventional and most update solutions. Robust analytical expressions were utilized to exploit the functionality of the proposed solutions and to show clearly the relation between the reactive power and control variables. The article, moreover, proposes a simple, innovative and robust analysis for static performance of the STATCOM. This approach shows clearly the advantages of the STA- TCOM in regulating reactive power and maintaining load voltage level within presumable limits. The approach, furthermore, reveals explicitly via analytical expressions the impact of the STATCOM operation on different aspects of the power system under concern.

Keywords:

Compensation, TCR, TSC, STATCOM, Reactive Power

1. Introduction

Reactive power flow is a salient feature of an electrical power system. Reactive power is mandatory for the operation of different load types either static or rotating [1] [2] . For example, in rotating load as induction motor, which is the main industry motor, the reactive power is essential for producing the revolving magnetic field required for successful operation. In the transmission and distribution networks of electric power, the reactive power is required to fulfill the requirement of proper operation. The value and the direction of the reactive power in such networks vary according to load level and power factor [1] [2] [3] . These lines are essentially reactive networks of distributed parameters characterized by their series inductance and shunt capacitance [4] [5] [6] [7] .

Reactive power flow, however, has a number of undesirable consequences. It increases the drawn current for the same load level, which in turn increases the losses, maintenance and cost of the power system operation. Moreover, it reduces the power stability margin. It under heavy level of reactive power probably results in voltage instability [8] [9] [10] [11] .

Different reactive power compensating strategies are reported in the literature. These schemes vary from simple techniques such as fixed capacitor/inductor to recent approaches such as Static Synchronous Compensator (STATCOM), Static Series Synchronous Compensator (SSSC) and Unified Power flow controller (UPFC) [12] [13] [14] [15] . The recent techniques as STATCOM, SSSC and UPFC are solid-state based circuits that manipulated DC voltage and DC current to synthesize the compensated voltage/current. These schemes are revolved from traditional solid-state topologies, Static VAR Compensators (SVC), such as Thyristor Controlled Reactor (TCR), Thyristor Switched Capacitor (TSC) and Thyristor Controlled Capacitor (TCC) [11] - [18] .

The compensating techniques either conventional or recent suffer from limitations. For example, the reactive output of SVC topologies is proportional to the square of the voltage magnitude. Therefore, the SVC provided reactive power decrease rapidly as voltage decreases, which reduces its stability. STATCOM typically exhibit higher losses and may be more expensive than SVC. Moreover, STATCOM operates under balanced operating conditions; thus its performance is deteriorated under abnormal operating conditions. The UPFC, also as STA- TCOM, could not operate properly under disturbance conditions [19] - [26] .

In this article, comprehensive analysis for the phenomenon of reactive power is provided. The different indices for the reactive power are highlighted. Then, examples of reactive power compensating scheme are addressed regarding operational constraints and performance characteristics. A simple and robust analysis for the static performance of the STATCOM is advised. Simple and clear analytical expressions are advised to expose explicitly the relation between the STATCOM and different aspects of power system operation. Finally, the conclusion highlights the main points in the dilemma of reactive power.

This article has a number of objectives:

1) Providing a comprehensive highlighting for conventional and recent techniques for compensating reactive power.

2) Analyzing the static/dynamic performance of different reactive power com- pensator as a simple straightforward approach.

3) Proposing simple and innovative approach for the static performance of the STATCOM, which illustrates via analytical expression the increase in load voltage and the reduction in transmission line losses due to STATCOM operation.

2. Reactive Power and Performance Indices

As mentioned before that reactive power is elementary for some load to function; therefore the majority of loads are functioning at lag power factor which is less unity. Figure 1 shows the variation of the power factor of a load with the drawn reactive power either inductive or capacitive. The active load power is assumed 1.0 pu in generating Figure 1.

Figure 1 shows that a load power factor is heavily dependent on the drawn reactive power and vice versa. Moreover, for inadequate design the load results in flowing large reactive power and hence degrading the power factor.

Reactive power flow, as mentioned, could result in uneconomic operation of the power system, as it increases the current magnitude and hence copper and reactive losses in the transmission and distribution networks. This is shown Figure 2. The power system in Figure 2 is assumed to operate at rated voltage and 1.0 pu active power, and the line under concern has a resistance of 0.1 pu. This hypothetical value for line resistance is assumed to depict the worst design case.

Figure 2 shows that current magnitude and losses increases for non-zero reactive power despite inductive or capacitive. This definitely impacts the economic operation of a power system, which eventually affects the end-line customers. To visualize the full dilemma of reactive power, Figure 3 shows the efficiency of 0.1 pu resistance power system versus the circulated reactive power. In producing Figure 3, only ohmic losses in the tranmission line are considered.

Figure 3 shows how could the flow of the reactive power impacts the efficiency. The figure shows that the efficiency is reduced under the flow of the reactive power despite its sign. This is attributed to the fact that Figure 3 is generated for uncompensated operation. The relatively low value around 90% of the efficiency at zero reactive power is due to the large value of the line resistance.

3. Reactive Power Compensation

Different techniques are emerged to remedy the problem of reactive power circulation. These approaches range from simple method to most-update approaches. Each approach enjoys merits and suffers from drawbacks. In the following, a concise highlight for these methods is addressed.

3.1. Simple Compensation Strategies

A simple compensation technique is inserting fixed capacitor/inductor [1] [2] [3] [4] . The capacitor is used for nominal/heavy load operating points to produce sufficient reactive power for boosting voltage profile at load buses. The inductor meanwhile is used for light load operating point to limit the voltage within the presumable regulation. Usually, the capacitor/inductor is inserted in the system via mechanical switch. The reactive power produced from reactive elements capacitor/inductor is obtained from the primitive equation,

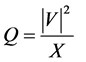(1)

where Q is either inductive or capacitive depending on X. The capacitive reactance powers produced via fixed capacitor elements are shown in Figure 4. This figure shows that pumped reactive power increases almost linearly with the capacitor value. This could be considered as a guideline for dimensioning the reactive power compensation element.

Figure 4 shows the linear dependency of the pumped reactive power from the capacitor with the capacitor value. This implies application of bulky and costly capacitor for compensating large loads. The reactive power produced from the fixed capacitor bank compensation is voltage dependent (Figure 4), as it varies with the square of the voltage at the common coupling point.

These techniques suffer from serious limitations, such as:

Fixed compensation, which limits their compensation ability;

Inability to respond for load requirements; these techniques fail to provide instantaneous response for load reactive power requirements;

Resonances, the fixed compensator capacitor/inductor values could resonate with transmission line parameters.

3.2. SVC Topologies

SVC gains more advantages than rotating reactive power compensators and fixed reactive elements, such as:

1) High efficiency;

2) Reduced volumetric dimension;

3) Relatively fast responses compared with synchronous condenser;

4) Adaptive operation, SVC could provide continuous compensation compared with fixed reactive elements. SVC could act as source/sink for the reactive power according to the control strategy;

5) Automation, as SVC are mainly solid-state devices, they could be controlled via intelligent systems as microprocessor and microcontroller.

It is worth to mention that SVC suffers from elevated harmonic content in the output voltage and current. This would produce additional problems to the power system.

SVC for shunt operation is composed from two main topologies. These are TCR and TSC, as shown in Figures 5-7. TCR and TSC could act independently generating inductive/capacitive reactive power, or they run as one device producing variable reactive power. In SVC, the reactive passive elements are interfaced to the common coupling point via self-commutated sold-state devices. TCR consists from inductance interfaced via pair of anti-parallel thyristors. The firing angles of the thyristors are controlled in continuous manner. For TCR, there are two modes of conduction: discontinuous current and continuous current. The inductor current is continuous if the firing angle α of the thyristor is greater than π/2 and less than π. For more details, see references [22] [24] . The inductor current is given in terms of firing angle,

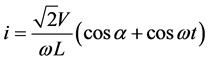(2)

The reactive power produced by TCR is given by,

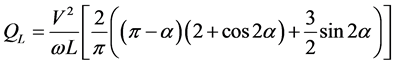(3)

Figure 6 shows the reactive power generated from TCR at different firing angles.

Figure 6 shows that for X_pu =1.0 the produced reactive power is 4 pu. A small inductor is sufficient to produce the required reactive power. The range of the firing angles of the thyristor is limited to be 90˚ - 180˚. This is to ensure continuous inductor current conduction.

TSC similarly to TCR is composed from capacitor interfaced to the common coupling point via pair of anti-parallel thyristors (Figure 7).

Here the thyristors are controlled such that current through the thyristor I_TCR is function in the thyristor firing angle, α. The RMS value of the current could be obtained by,

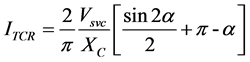
Thus, the reactive power could be calculated by,

For more details, see references [22] [24] .

The thyristor RMS current and the capative reactive power are function in thyristor firing angle, α. The reactive powers as a function in thyristor firing angle and the capacitance are shown in Figure 8.

Figure 8 shows that as the firing angle increases the delivered reactive power decreases. Therefore, the reactive power diminishes at high firing angles (Figure 8). The capacitive reactive power is inversely proportional with capacitance value, (8).

TCR and TSC are usually merged in topology themed SVC (Figure 9). This widens the applicability range of the SVC and allows compensation of different load levels.

The characteristics of SVC are shown in Figure 10. SVC in Figure 10 is composed of TCR and TSC topologies.

Figure 10 shows that SVC for voltage below 1 pu operates as TSC, while for higher voltage level than 1 pu, it acts as TCR. SVC, Figure 10, has the ability to generate and or absorb reactive power accordingly to the load level and power factor.

3.3. STATCOM

STATCOM is the recent configuration of SVC; it remedies the limitations in the traditional SVC. STATCOM generally utilizes high sufficient frequencies such that STATCOM produces high quality output voltage and current. The main objective of the STATCOM is to produce instantaneous +/- reactive power according to the load requirement and the operating point. Figure 11 shows a power system where the STATCOM is attached at the point of common coupling. The STATCOM is usually interfaced via a transformer.

STATCOM consists of mainly a Voltage Source Converter (VSC) attached to large DC capacitor. Fully controlled solid-state devices are used to implement VSC. The basic objective of a VSC is to produce a sinusoidal ac voltage with minimal harmonic distortion from the DC voltage. The DC voltage across the DC capacitor (CDC) of the STATCOM is controlled to be constant. The DC capacitor has the function of establishing an energy balance between the input and output during the dynamic performance of the STATCOM. The size of the capacitor is primarily determined by the ripple input current encountered with the particular converter design [4] [27] .

Static Performance of STATCOM

Static performance of the STATCOM could be obtained from the equivalent circuit shown in Figure 12. This circuit depicts the steady-state performance of a load connected to a supply via a transmission line with inductive and resistive losses. The load voltage V_L is taken as a reference (Figure 12). The STATCOM is modeled as a variable current source, which generates current component that eliminates the reactive component of load current. Therefore, the supply pumps only active power and reactive power required to compensate transmission line inductive drop.

The supply voltage amplitude IV_sI = 1.0. The supply angle δ is given by

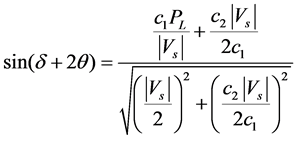(4)

where P_L is load power and the angle θ is given by

(5)

where c₁ and c₂ are given respectively by,

(6)

(7)

The load voltage is given by,

(8)

The STATCOM modeled current source is given by,

(9)

The graph of load voltage V_L is shown in Figure 13 without compensation for different load levels and power factors along with compensated scenario. The load voltage illustrated in Figure 13 is obtained by Equation (8).

Figure 13 shows that the system operation with STATCOM results in better load voltage profile. However, as the STATCOM is attached at load bus; thus the supply has to deliver the required reactive power to fulfill the requirements of transmission line. Figure 13 shows for lag load a significant drop for load voltage is recorded, which maybe not suitable for voltage sensitive loads.

The influence of the STATCOM on the transmission line losses are shown in Figure 14, where transmission line losses are drawn versus load power for different load power factor.

It is obvious in Figure 14 that operation of the system under concern while deploying STATCOM results in minimum line current amplitude and hence minimum transmission line losses. Figure 14, shows for uncompensated operation the lead power load scenarios reduce transmission line losses compared to lag power factor scenarios.

The reactive power delivered by STATCOM under different load and power factor levels is illustrated in Figure 15.

Figure 15 reveals the merit of STATCOM in instantaneous responding for load reactive requirements. However, Figure 15 shows hypothetical operating conditions, such as the operation close to power equal of 0.1 lag/lead. Moreover, the figure ignores the operational limits of the STATCOM, which are returned to storage capacity of the DC source and ratings of solid-state devices.

4. Conclusions

A comprehensive overview for the problem of reactive power and different compensating techniques are given in this article. The reactive power is mandatory for operating a power system as different types of loads require reactive power to function. These loads include rotating and staticas induction motor and light loads. However, the circulation of the reactive power influences the operation of different power system components and subsystems such as transmission lines and cables. Moreover, significant voltage drop is produced due to the flow reactive power, which could result in voltage instability.

Different compensation techniques are developed and adopted in the power system. The fixed reactive passive elements produce reactive power that is voltage dependent. Moreover, resonances could be produced due to the interaction of reactive elements with the transmission lines and power system reactances.

Conventional SVC configurations as TCR and TSC emit significant harmonics into common coupling point.

STATCOM enjoys the advantages of fast response, robustness and reliability. STATCOM produces continuous reactive power according to the loading conditions.

Acknowledgements

The authors are grateful for Shaqra University and College of Engineering for supporting and encouraging this work in particular Prof. Dr. Abdulaziz S. Alsayyari, dean of Engineering College.

Cite this paper

AbdElhafez, A.A., Alruways, S.H., Alsaif, Y.A., Althobaiti, M.F., AlOtaibi, A.B. and Alotaibi, N.A. (2017) Reactive Power Problem and Solutions: An Overview. Journal of Power and Energy Engineering, 5, 40-54. https://doi.org/10.4236/jpee.2017.55004

References