ABSTRACT

Solar cells are well known as devices for sustainable electric energy generation. Nowadays the potential induced degradation has been brought up as an obstacle problem for practical use. In order to determine the cause of this kind of degradation, numerical simulation by a finite difference time domain method has been performed for computational electromagnetics in the case that the thunder attacks the solar modules. The results show that the dielectric breakdown in the glass covered over the solar cells triggered by the thunderstroke is critical. So it is helpful to protect the dielectric breakdown in the glass from the thunderstroke.

Keywords:

Solar Cell, Potential Induced Degradation, Thunderstroke, Leakage Current

1. Introduction

Solar cells are quite attractive devices to generate electricity without any environmental disturbance such as thermal or atomic power generation of electricity [1] [2] . The one solar cell provides a voltage as small as 1 V. Then many cells are used by connecting them in series to give several hundred volts, sometime even more than one thousand volts. It is because the higher voltage can be transferred by electric line with the less energy loss.

As early as 1978, it has been already reported that solar cells have an intrinsic problem that high potential can induce degradation. This potential induced degradation has attracted more attention since Swanson et al. reported the degradation up to 30%. Thereafter, more and more attention has been paid to this practical obstacle for solar cell applications. The potential induced degradation [3] [4] [5] is now a main theme for the improvement of the solar cell durability. But the cause for the degradation has not yet been clarified enough. It is partly because it takes no less than one year to induce full degradation. Anyway, the degradations including others are now a big issue for practical use [6] .

Solar panels are usually installed on the roof or on the ground, in the rigorous circumstances of nature. We focus on the thunderstroke to the solar panels; the thunder induces high voltage where the solar panels are exposed to it. We assume that the thunderstroke induced dielectric breakdown in insulators in the module, which results in the increase of leakage current in the module.

The solar cell module consists of glass cover, a back sheet and an aluminum frame. The leakage current can be classified into the three parts. This article aimed to clarify the degradation part and to acknowledge the degradation mechanism. For this purpose, a simulation study has been performed on the basis of a finite difference time domain method with Maxwell’s electromagnetic equations.

2. Theory

The basic equations treated here are Maxwell’s electromagnetic equations:

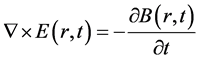
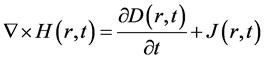
Using B = μ H, D = ε E and J = σ E, we obtain the equations:

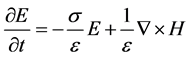
These equations were transferred to difference equations. In order to perform the numerical calculation, the process was based on the well-known Yee algorithm [7] . Actual calculation steps are shown in the literature. We used the differential-based absorbing boundary condition proposed by Mur [8] .

All the spatial finite differences Δx, Δy and Δz should be under a tenth of the wave length. As for the time finite difference Δt, it should be consistent with the Courant condition that is

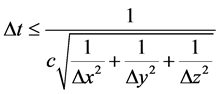
3. Modelling

The solar cell panel treated here is described. Figure 1 shows the top and bottom view of the panel in (a) and a sectional view in (b). The panel consists of three layers of a glass plate, a solar cell and EVA for encapsulation, and back sheet (PET) from the surface to the bottom. The panel was fixed by an aluminum frame around it. The solar cell itself was treated as a perfect conductor. It was assumed that water exists on the glass to simulate a rainy weather.

The analytical model of the solar cell panel is shown in Figure 2. The aluminum frame was earthed through 10 Ω at the four corners. The two output terminals were shunted and then earthed through 500 kΩ. The earth is expressed as a perfect conductor with the thickness of 0.01 m. The electromagnetic parameters such as relative dielectric constant, relative permeability, and electric conductivity for each material are shown in Table 1.

We describe here the model of thunderstroke where only the indirect thunderstroke was considered. The thunder current was located at the point P in Figure 2 and flowed along the z axis. The parameter LX and LY was 0.3 m. The wave of the thunder current was formed by the step voltage for the tail that ranges from 20 kA or 70 kA with a head voltage whose width was between 0.1 μs. The current was uniform along the z axis.

Unit: S/m.

Analytical space was in the area of 1.6 m × 1.6 m × 0.4 m. The differences of Δx, Δy and Δz are 10 mm, 10 mm, and 1 mm, respectively. In order to satisfy the Courant condition, the time difference was set to 1 ps. We took the 300,000 time steps that are far larger than the head voltage width.

We defined V1, V2, and V3 as shown in Figure 3. The calculated voltage was taken near the point O in Figure 2 and another point where electric field was concentrated. In order to confirm the field-concentrated point, the profile of the electric field in each material was examined at first.

4. Results and Discussion

Figure 4 shows the profiles of the electric field induced at the bottom of the back-sheet, where both LX and LY was 0.3 m, the head width and the magnitude of the thunderstroke current were 0.1 μs and 20 kA, respectively. At 3 ns, electric

field waves were found to spread outward from the point M. At 3.5 ns, it can be seen that the wave is accumulated as it reached the right end. At 4 ns, the reflected waves are seen from both the upper and the lower sides toward the center. At 0.1 μs, all waves are mostly disappeared. The height of the wave is maximized at the aluminum frame in all the figures. The fact was also observed on the surface of the back-sheet and on the glass layer. Thus, the voltage was calculated in the vicinity of the aluminum frame.

We next consider the V1, V2 and V3 as a function of time. The calculated results are shown in Figure 5 and Figure 6. Figure 5 shows V1 and V2 variations along the time as well as the thunderstroke current of I. The I was a step voltage of which the head width was 0.1 μs and the height was 20 kA. The V1 has the largest spike that marked 21 kV at maximum and the spike voltage gradually decreases till 0.15 μs. On the other hand, V2 is no more than 5 kV. The voltages at

point O shown in Figure 6 are far smaller than those near the aluminum frame, as is consistent with the discussion in Figure 4.

We next consider the effect of water on the glass plate. The height of the current was 70 kA here. The voltages of V1 and V2 are shown in Figure 7. These results are the case that water exists on the glass. The maximum voltage is up to 60 kV across the glass. Since the thickness of the glass was 3 mm, the electric field can be estimated to be 20 kV/mm. This value is no less than the dielectric strength of ordinary glass. The calculated results without water on the glass are shown in Figure 8. It is interesting that the maximum voltage spike was less than 30 kV on the contrary. And V1 was reduced to be similar to V2 in this case. From this fact, water on the glass seems to be a main role to induce dielectric breakdown in the glass layer. However, the mechanism of the role is not yet clarified physically.

5. Conclusion

The potential induced degradation is one of the biggest problems for practical use of solar cell panels. In order to clarify the degradation mechanism, numerical calculations were performed in the case of thunderstroke, based on the Maxwell’s electromagnetic equations. The results have shown that the electric field was induced over the panel, especially strong at the aluminum frame. When the thunderstroke current was 70 kA, the electric field induced in the glass that covered the solar cells reached the dielectric strength of 20 kV/mm. It was also found that the existence of water over the glass raised the induced electric field to a great extent. The dielectric breakdown in the glass was found to be a main cause of the potential induced degradation in this study.

Cite this paper

Ohmukai, M. and Tsuyoshi, A. (2017) Simulation Suggests Origin of Potential Induced Degradation of Solar Cell. Journal of Power and Energy Engineering, 5, 43-49. https://doi.org/10.4236/jpee.2017.56004

References