Journal of Power and Energy Engineering
Vol.05 No.01(2017), Article ID:73518,22 pages
10.4236/jpee.2017.51004
Secure Operation and Optimal Generation Scheduling Considering Battery Life for an Isolated Northwest Grid of Saudi Arabia
Hani Albalawi, Karthikeyan Balasubramaniam, Elham Makram
Department of Electrical and Computer Engineering, Clemson University, Clemson, USA

Copyright © 2017 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: November 21, 2016; Accepted: January 14, 2017; Published: January 17, 2017
ABSTRACT
Maintenance schedule of generators in an interconnected power system presents multifaceted challenges, two important ones being optimal operation cost and secure operation. When a generator is scheduled for maintenance, achieving optimal generation scheduling for the committed generators is necessary but it is not sufficient for secure operation of power systems. This problem is decomposed into two subproblems: i) Finding the optimal set points for the generators; ii) Validating secure operation with those set points from i). Both these subproblems [i) and ii)] have been studied extensively in the literatures. However, the research here focuses on incorporating battery energy storage systems (BESS) in power operation, a renewable generation that can provide smooth and flexible reserves of power, an area that has not yet been fully explored. In addition, incorporating BESS while considering both the cost implications and addressing secure operation has not yet been addressed in previous literatures. The purpose of this paper is to present both secure and optimal operation besides improving the longevity of the BESS. Feasibility of the proposed approach is demonstrated on Tabuk region―an isolated northwest grid of Saudi Arabia.
Keywords:
Optimal Cost, Secure Operation, Battery Life, Forced Contingency

1. Introduction
With increasing load demand, renewable generation has provided a viable means for reducing emissions and operational costs. In particular, the use of solar generation has seen a significant increase over the last decade. However, the random power output of PV has created several challenges in power system operation and control. Renewable generation is categorized as non-load following generation as its output cannot be controlled. The inter-dispatch variability of renewable generation that is geographically distributed, to a large extent, is smooth. However, scenarios such as the one considered in this work where the renewable generators are not geographically distributed present a considerable challenge with respect to variability and availability [1] . One of the solutions potentially addressing the challenge of solar variability is to use battery storage, which has been found to be particularly effective when working in parallel with PV in peak load shaving as presented in [2] [3] . Renewable energy systems today are sufficiently developed and are widely used to address environmental and economic dispatch (ED) concerns. Storing energy at off-peak times when there is additional generation capacity and then using this stored energy will make the economic dispatch (ED) more efficient in terms of operating cost. Time shifting renewable energy generation through the use of BESS will help reduce the operating cost in this scenario as the incremental cost of producing power through controllable generation is lower at certain levels of loading [4] .
Many studies have been introduced for optimal operation with PV and battery storage. For example, the Authors in [5] presented an optimal battery scheduling plan with emission constrains to reduce the carbon footprint of conventional thermal units. Reference [6] proposed an optimal peak shaving by managing energy storage devices, and the research presented in references [7] [8] proposed optimal charging/discharging scheduling of BESS to minimize line losses in distribution systems. In [9] an optimal power management for grid connected PV system with batteries is proposed to minimize customer energy bills, and an optimal scheduling of battery storage presented in [10] is used to evaluate the optimal amount of installed battery into the grid by considering the CO2 emission in the economic evaluation. The authors in [11] proposed an optimal scheduling of non-utility facility with battery storage under a price taking scheme. None of these studies, however, considered the battery life in the cost function. Disregarding the battery life in optimal power scheduling is an unrealistic scenario. Although BESS lowers operating costs, the life of the battery is significantly reduced. As BESS requires substantial investment, it is imperative that they be used effectively and efficiently such that the economic and security margins of the power grid operation are maximized.
This paper presents an optimal generation scheduling taking into consideration renewable energy sources, BESS usage cost, and secure operation. In addition, it also proposes an optimal generation schedule considering battery life and short term outages: resulting in extended battery life and finding a solution during outages without affecting the optimal operation. Feasibility of this proposed approach is demonstrated using Tabuk power system―an isolated northwest grid of Saudi Arabia.
The outline of this paper is as follows: Section 2 shows the PV farm output power. Section 3 defines the usage cost that introduced to extend the battery life. Section 4 discusses the optimization problem formulation and constraints. Section 5 explains the forced contingency analysis implemented for secure operation during optimal operation. Section 6 provides a brief description of the test system. Section 7 discusses the simulation result.
2. PV Output Power
The summer irradiation data for Tabuk city used here was taken from Renewable Resource Atlas of Saudi Arabia [12] . The station data is located at Tabuk University. Figure 1 shows the irradiation profile for 31 August 2015. To simulate the PV output power of the farm, the Wavelet Variability Model Toolbox in Matlab was used; the details and validation of this model are described in [13] [14] . In this paper, a 100 MW solar PV farm is simulated to be included in the optimization process. Figure 2 illustrates the PV power for the solar farm.
3. Battery Usage Cost
The levelized cost of the battery is adopted in defining the usage cost to quantify
Figure 1. Irradiation data.
Figure 2. PV output power.
the charge/discharge cycle in the optimization process. Thus, the formulation explicitly involves the life cycle of the BESS based on the definition of a usage cost as given in Equation (1), which imposes the physical degradation of the BESS. Excluding the life cycle creates unrealistic situation and exaggerates the significance of BESS on system operation at minimum cost. The cost of the battery is not estimated; rather it is specified based on the battery markets and prices for large scale storage. The goal here is to achieve minimum operational cost while at the same time extend the life of the battery by using it only when needed.
The levelized cost of energy (LCOE), which provides a more accurate reflection of the actual cost of a given battery, helps to determine the cost ($/kwh) involved in charging and discharging the battery over its lifetime. This cost is used as the usage cost for the battery. The LCOE is calculated as follows [15] ;
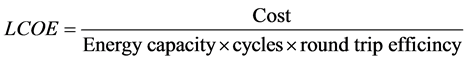 (1)
(1)
The cost in Equation (1) includes installation costs, variable and fixed operation and maintenance costs. Moreover, the battery replacement cost is also involved since the battery will be replaced once, at the year 8 of a 15-years period. A lead acid battery is used and the battery data with its cost are based on the battery markets and prices [16] . Table 1 shows the battery parameters and cost.
Thus,
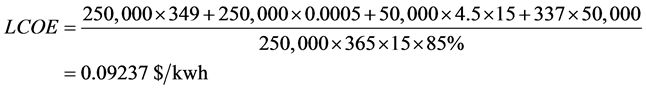
4. Problem Formulation
Many methods have been used by the power industry to solve economic dispatch problems in order to minimize the operation cost. The complexity of the
Table 1. Battery data and cost [16] .
problem and the economic benefit gained from cost minimization have motivated both the academia and the industry to develop improved optimization techniques [17] , resulting in such promising methods such as Lagrangian Relaxation, Dynamic Programming, Branch and Bound Mixed Integer Programming and Bender Decomposition Methods [18] [19] [20] . Recent developments in integer programming propose additional promising methods to acquire improved solutions for large scale systems more rapidly [17] . In this work, the fuel cost curve is approximated using a quadratic function. Hence, the ensuring formulation is of mixed integer quadratic programming (MIQP) type.
4.1. Energy Storage
Equation (2) below is the energy balance equation of the (BESS) [21] , while Equations (3)-(5) give the bounds for the rate of charge and discharge and the battery storage limits.
 (2)
(2)
 (3)
(3)
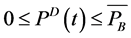 (4)
(4)
 (5)
(5)
Equation (2) is of particular importance because  and
and  are free variables that could take non-zero values in any dispatch. However, in reality the BESS can either charge or discharge during a given interval but not both. This condition is enforced with the use of a binary variable such as
are free variables that could take non-zero values in any dispatch. However, in reality the BESS can either charge or discharge during a given interval but not both. This condition is enforced with the use of a binary variable such as
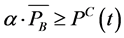 (6)
(6)
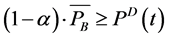 (7)
(7)
Although Equations (6) and (7) ensure that only charging or discharging occurs during a given dispatch, such a modeling requires the use of the binary variable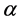 , increasing the computation effort required to solve the problem. Instead, the need for binary variables is avoided because of their implicit inclusion in the objective function. As Charging and discharging in the same dispatch result in an inefficient use of the energy and, hence, would increase the total cost, the optimizer would never charge and discharge at the same dispatch and instead schedules charging and discharging in an optimal manner.
, increasing the computation effort required to solve the problem. Instead, the need for binary variables is avoided because of their implicit inclusion in the objective function. As Charging and discharging in the same dispatch result in an inefficient use of the energy and, hence, would increase the total cost, the optimizer would never charge and discharge at the same dispatch and instead schedules charging and discharging in an optimal manner.
4.2. Power Balance Equation
Equation (8) is the power balance equation. The algebraic sum of the power generated by generators, the PV power and the BESS should equal to the power demand for all dispatches.
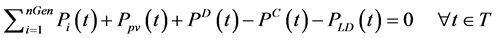 (8)
(8)
4.3. Generation Limit
The amount of power generated and the ramp up/down rate for each generator is constrained as follows:
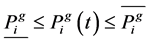 (9)
(9)
 (10)
(10)
4.4. Fixed Cost for the Generator
The fixed cost for the generator was model as seen in Equation (11), where  is a binary variable. Hence, whenever non-zero power is produced by the ith generator
is a binary variable. Hence, whenever non-zero power is produced by the ith generator

4.5. Startup Cost
Equation (12) ensures that 

4.6. Objective Function
The cost function, defined as the fuel cost of all generators, the startup cost and the battery usage cost, is formulated as follows:

where



5. Forced Contingency Analysis
Forced contingency can be described as any outage of a grid component such as a line or a transformer and/or a generator due to a fault. These outages can cause voltage or line limit violations due to the resulting overloading. A contingency, thus, is defined as a possibly harmful disturbance that may occur during operation. However, in normal operation conditions, contingency analysis is used under heavily loaded systems to provide a list of lines to be ranked in order to help relieve the overloading of the system by removing a line (N-1). If one line does not relieve the overload, then another line is removed (N-1-1).
This paper focused in forced contingency during optimal operation to provide the operators with an overview of the system and a solution for any of the outages in order to maintaining optimal operation. Hence, different cases will be applied to the system. For each case, the optimal operation cost is obtained, followed by a line outage due to a fault. An improved solution for any outage may be provided by removing another line to ensure optimal operation is maintained without any violations.
6. Test System
This optimization approach based on MIQP was applied to the isolated northwest grid in Tabuk city consisting of 12 buses as shown in Figure 3 and Figure 4, with a voltage level of 132 KV. It includes two generation stations, connected at Buses 1 and 5, consisting of 25 units with total capacity of 959.2 MW. The generation capacity and age of each unit are shown in Table 2. A standard IEEE fuel cost curve and a fixed startup cost, shown in Table 3, were used for the newest unit, while the cost curves of the remaining generators have been modeled based on the unit’s age by decreasing the efficiency of the standard one, meaning that newer generators have lower fuel cost than the older ones. Since the age of each unit is based on 2013, a load curve for a summer day in July of that year was used for the simulation, with the load profile and lines data being provided by the Saudi Electricity Company (SEC), Tabuk sector.
7. Simulation Result
From the recorded data obtained for the summer day used in this study, the peak loading condition was used as the worst case scenario for the test system. On that day, the generated power at peak load occurred at 4 pm with a total load of 720 MW. The battery storage constraints used in the simulation shown in Table 4 are based on the battery data given in Table 1. The dispatch interval was every 15 minutes, with a specified ramp up/down of 2 MW/min. The model was implemented in MATLAB using CPLEX [23] to solve MIQP. The performance of the optimization problem can be measured by the integrality gap, defined as the gap between the optimal value of the relaxed solution and the optimal integer solution [24] [25] .
Different situation were applied to the system, with optimal operation cost being obtained for each. In addition, forced contingency analysis was implemented
Figure 3. Single line diagram of the test system [26] .
Table 2. This table shows all generators (diesel) capacity [22] .
Table 3. Standard IEEE coefficient for the fuel cost curve [10] .
Table 4. This table shows battery constraints.
by tripping a line (N-1) due to a fault. When such a violation occurred, a search of a solution for any overloaded lines was obtained. Violation was addressed by removing another line (N-1-1) to maintain the stability of the system. Similarly, the cases can be extended to generators/transformers maintenance scheduling, with such cases involving removing one or more generators from Tabuk-2. The specified cases investigated in this paper include the follows:
1. Case A: All generators in Tabuk-2 are ON, full capacity 959.2 Mw.
2. Case B: One large generator in Tabuk-2 is scheduled for maintenance, remaining capacity 881.2 Mw.
3. Case C: Two largest generators in Tabuk-2 are scheduled for maintenance, remaining capacity 803.2 MW.
4. Case D: Three largest generators in Tabuk-2 are scheduled for maintenance, remaining capacity 737.7 Mw.
5. Case E: Four largest generators in Tabuk-2 are scheduled for maintenance, remaining capacity 673.2 Mw.
Table 5 shows the optimal operation cost of one minute simulation for the different cases. These particular cases are used here to determine whether the PV and battery can help in meeting demand with minimum operation cost or if they are able to replace generation in Tabuk-1 since it is an old station (≥30 years old) with a high operating fuel cost. For the first scenario of each case, except for Case E, the optimal operation cost is achieved when the PV is included without any penetration from Tabuk-1. Case E required Tabuk-1 to operate with both PV and battery to help to meet the demand with minimum operation cost because of the lack of power when four generators are out-of-service due to maintenance scheduling. Hence, the PV with the battery storage can replace Tabuk-1. Without the PV, (as shown in Cases C, D and E) Tabuk-1 with the battery helped the system to meet the demand at optimal operation cost even in the most extreme case when four generators are out-of-service due to a long term outage or maintenance.
Table 5. This table shows the optimal operation cost for all the cases.
In this study, three cases with results are selected. Figure 5 shows the simulation results for the first scenario of Case C when the two largest generators in Tabuk-2 were out-of-service for maintenance. As the results indicate, the energy stored in the battery operated within the battery energy limits. The power contribution of Tabuk-2 is presented in Figure 5(c); it was the only station with PV and BESS supplied the demand with optimal operation cost as shown in Table 5. As seen in the demand and supply graph in Figure 5(a), the battery began to charge approximately at 10 a.m. when extra power was available at minimum load, and then discharging at 4 p.m. and 10 p.m.
Figure 6 shows the simulation results for the second scenario in Case D. Since the PV and three largest generators in Tabuk-2 were not in operation, the battery helped to meet the demand at peak load by charging earlier in the day. Figure 6(a) shows the battery charged twice, once at approximately 4 a.m. and again at 7 a.m. when there was extra power and then discharged later in the day at peak load, which occurred at 4 p.m., to support the demand. The amount of power generated from each generator is shown in Figure 6(c) and Figure 6(d).
Figure 7 illustrates the results of the most extreme case when the PV and the four largest generators in Tabuk-2 were out-of-service for maintenance. As shown in Figure 7(a), the battery helped to meet demand by charging twice early in the morning for almost 8 hours in total. The lack of power during peak time was compensated by discharging the battery from 2 p.m. to 6 p.m. when all generators were operating at full capacity of 673.2 MW. A second charging and discharging process occurred from approximately 8:30 p.m. to 10 p.m. respectively as shown in Figure 7(a).
Minimum operation cost and extended battery life have been achieved for all cases presented in Table 5. To determine the importance of including the battery life in the cost function, the usage cost of the battery is neglected. Figure 8 and Figure 9 show the simulation results of two selected cases to illustrate the



Figure 5. Simulation result for case C scenario 1: (a) Demand and supply, (b) BESS energy and (c) Scheduled power for Tabuk-2.




Figure 6. Simulation result for case D scenario 2: (a) Demand and supply, (b) BESS energy, (c) Scheduled power for Tabuk-1, and (d) Scheduled power for Tabuk-2.




Figure 7. Simulation result for case E scenario 2: (a) Demand and supply, (b) BESS energy, (c) Scheduled power for Tabuk-1, and (d) Scheduled power for Tabuk-2.




Figure 8. Simulation result for case B scenario 1: (a) and (c) BESS charging/discharging, (b) and (d) BESS energy. (a and b) Battery usage cost included, (c and d) Battery usage cost excluded.




Figure 9. Simulation result for case B scenario 1: (a) and (c) BESS charging/discharging, (b) and (d) BESS energy. (a and b ) Battery usage cost included, (c and d) Battery usage cost excluded.
impact of the battery life both with and without the battery usage cost. The purpose of including the usage cost for the battery is to extend its life. In addition, the BESS has an associated life cycle that should be considered to achieve optimal utilization of the battery. Charging/discharging the battery freely will impact the battery life cycle. Figure 8 and Figure 9 show the impact of the battery life on the objective function. When the battery life is included, the BESS is utilized for two cycles while it is utilized for 4 cycles when the battery life is omitted as seen in Figure 8(a) and Figure 8(c). In the cases seen in Figure 9(a) and Figure 9(c), the number of cycles increased from 1 to 3 cycles when the battery usage cost was not considered. Table 6, which summaries the number of cycles utilized in each case, indicates a significant improvement to extend the battery life. In addition, more power is used for both charging and discharging process as more energy is stored since the battery is charging/discharging freely as shown in Figure 8(d) and Figure 9(d).
After achieving optimal operation cost and extended battery life the peak loading condition, which occurred at 4 p.m., is selected as a worst case scenario to validate secure operation. For each case, 18 forced contingency (N-1) are applied individually due to a fault since the system has 18 lines as shown in Table 7. For each contingency if a violation has occurred, another line is removed (N-1-1) in order to help relieve the overload.
In all cases, a violation is considered if a line achieves a 100% or more of its capacity. Table 8 shows the optimal generated power at peak loads for each case with the PV and battery penetration. Due to the size of the PV farm, it is not feasible to locate the PV farm within residential areas as it requires a large land area to accommodate it. Hence, the ideal location is near Bus 6 [26] .
Table 9 shows only the cases where violations observed for any forced con-
Table 6. This table shows number of cycles performed for each case.
Table 7. Line and peak load data.
Table 8. Optimal generated power at peak loads for each case with PV and battery.
Table 9. Observed violation cases.
tingency as well as solution for relieving the overloaded lines. In these cases, the violations occurred only at line 5-6, which is mostly responsible for the delivery of power at Bus 9 that has the largest load. However, when the PV or Tabuk-1 is operating with the battery no violation occurred.
8. Conclusion
In this paper, an MIQP based optimization problem was formulated in order to find the optimal operation schedule for generators in an isolated northwest grid of Saudi Arabia in the presence of renewable generation and battery storage. The BESS was embedded in the optimization problem by introducing a usage cost based on battery markets and prices for a large-scale storage. The results show substantial improvement both in the longevity of the BESS and in the economic and secure operation of the test system. This paper also presented various cases to evaluate system reliability for any short term outages during optimal operation. Feasible solutions were provided for the violations investigated in order to maintain an optimal operation cost for a power system.
Cite this paper
Albalawi, H., Balasubramaniam, K. and Makram, E. (2017) Secure Operation and Optimal Generation Scheduling Considering Battery Life for an Isolated Northwest Grid of Saudi Arabia. Journal of Power and Energy Engineering, 5, 41-62. http://dx.doi.org/10.4236/jpee.2017.51004
References
- 1. Marwali, M.K.C., Haili, M., Shahidehpour, S.M. and Abdul-Rahman, K.H. (1998) Short Term Generation Scheduling in Photovoltaic-Utility Grid with Battery Storage. IEEE Transactions on Power Systems, 13, 1057-1062.
https://doi.org/10.1109/59.709099 [Paper reference null] - 2. Chowdhury, B.H. and Rahman, S. (1988) Analysis of Interrelationships between Photovoltaic Power and Battery Storage for Electric Utility Load Management. IEEE Transactions on Power Systems, 3, 900-907.
https://doi.org/10.1109/59.14539 [Paper reference null] - 3. Fischl, R., Herczfeld, P.R., Halprin, T.F. and Stewart, D.B. (1979) Design of Integrated-Electric-Solar-Utility System for Peak Load Shaving. Proceedings of the IEEE Power Engineering Society Winter Meeting, New York, 4-9 February 1979, 102-105. [Paper reference null]
- 4. Pazheri, F.R., Othman, M.F., Malik, N.H. and Safoora, O.K. (2012) Economic and Environmental Dispatch at Highly Potential Renewable Area with Renewable Storage. International Journal of Environmental Science and Development, 3, 177-182.
https://doi.org/10.7763/IJESD.2012.V3.211 [Paper reference null] - 5. Haddadian, G., Khalili, N., Khodayar, M. and Shahidehpour, M. (2015) Optimal Scheduling of Distributed Battery Storage for Enhancing the Security and the Economics of Electric Power Systems with Emission Constraints. Electric Power Systems Research, 124, 152-159.
https://doi.org/10.1016/j.epsr.2015.03.002 [Paper reference null] - 6. Levron, Y. and Shmilovitz, D. (2012) Power Systems’ Optimal Peak-Shaving Applying Secondary Storage. Electric Power Systems Research, 89, 80-84.
https://doi.org/10.1016/j.epsr.2012.02.007 [Paper reference null] - 7. Teng, J.H., Luan, S.W., Lee, D.J. and Huang, Y.Q. (2013) Optimal Charging/Dis- charging Scheduling of Battery Storage Systems for Distribution Systems Interconnected with Sizeable PV Generation Systems. IEEE Transactions on Power Systems, 28, 1425-1433.
https://doi.org/10.1109/TPWRS.2012.2230276 [Paper reference null] - 8. Ziadi, Z., Taira, S., Oshiro, M. and Funabashi, T. (2014) Optimal Power Scheduling for Smart Grids Considering Controllable Loads and High Penetration of Photovoltaic Generation. IEEE Transactions on Smart Grid, 5, 2350-2359.
https://doi.org/10.1109/TSG.2014.2323969 [Paper reference null] - 9. Riffonneau, Y., Bacha, S., Barruel, F. and Ploix, S. (2011) Optimal Power Flow Management for Grid Connected PV Systems with Batteries. IEEE Transactions on Sustainable Energy, 2, 309-320.
https://doi.org/10.1109/TSTE.2011.2114901 [Paper reference null] - 10. Oka, Y. and Yokoyama, A. (2013) Optimal Operation Scheduling and Economical Evaluation Method of Battery Energy Storage System in Power System with a Large Penetration of Photovoltaic Generation. IEEE PowerTech (POWERTECH), Grenoble, 16-20 June 2013, 1-6.
https://doi.org/10.1109/ptc.2013.6652320 [Paper reference null] - 11. Nuchprayoon, S. (2015) Optimum Scheduling of Non-Utility Facility with Battery Storage under a Price-Taking Scheme. IEEE PowerTech, Eindhoven, 29 June-2 July 2015, 1-6.
https://doi.org/10.1109/ptc.2015.7232608 [Paper reference null] - 12. Renewable Resource Atlas of Saudi Arabia.
https://rratlas.kacare.gov.sa [Paper reference null] - 13. Lave, M. and Kleissl, J. (2012) Testing a Wavelet-Based Variability Model (WVM) for Solar PV Power Plants. IEEE Power and Energy Society General Meeting, San Diego, 22-26 July 2012, 1-6.
https://doi.org/10.1109/PESGM.2012.6344951 [Paper reference null] - 14. Lave, M., Kleissl, J. and Stein, J.S. (2013) A Wavelet-Based Variability Model (WVM) for Solar PV Power Plants. IEEE Transactions on Sustainable Energy, 4, 501-509.
https://doi.org/10.1109/TSTE.2012.2205716 [Paper reference null] - 15. Levelived Cost of Energy Storage, Renew Economy.
http://reneweconomy.com.au/2015 [Paper reference null] - 16. Akhil, A.A., Huff, G., Currier, A.B., Kaun, B.C., Rastler, D.M., Chen, S.B. and Gauntlett, W.D. (2013) DOE/EPRI 2013 Electricity Storage Handbook in Collaboration with NRECA. Sandia Report: SAND2013-5131, Sandia National Laboratories, Albuquerque. [Paper reference null]
- 17. Srinivasan, D. and Logenthiran, T. (2009) Short Term Generation Scheduling of a Microgrid. IEEE TENCON, Singapore, 23-26 January 2009, 1-6. [Paper reference null]
- 18. Ongsakul, W. and Petcharaks, N. (2004) Unit Commitment by Enhanced Adaptive Lagrangian Relaxation. IEEE Transactions on Power Systems, 19, 620-628.
https://doi.org/10.1109/TPWRS.2003.820707 [Paper reference null] - 19. Ouyang, Z. and Shahidehpour, S.M. (1991) An Intelligent Dynamic Programming for Unit Commitment Application. IEEE Transactions on Power Systems, 6, 1203- 1209.
https://doi.org/10.1109/59.119267 [Paper reference null] - 20. Padhy, N.P. (2004) Unit Commitment—A Bibliographical Survey. IEEE Transactions on Power Systems, 19, 1196-1205.
https://doi.org/10.1109/TPWRS.2003.821611 [Paper reference null] - 21. Baker, K., Hug, G. and Li, X. (2014) Optimal Storage Sizing Using Two-Stage Stochastic Optimization for Intra-Hourly Dispatch. North American Power Symposium (NAPS), Pullman, 7-9 September 2014, 1-6.
https://doi.org/10.1109/naps.2014.6965384 [Paper reference null] - 22. Electricity & Cogeneration Regulatory Authority (ECRA).
http://www.ecra.gov.sa/ar-sa/dataandstatistics [Paper reference null] - 23. The ILOG CPLEX.
https://www.ibm.com/developerworks/downloads/ws/ilogcplex/ [Paper reference null] - 24. Carrión, M. and Arroyo, J.M. (2006) A Computationally Efficient Mixed-Integer Linear Formulation for the Thermal Unit Commitment Problem. IEEE Transactions on Power Systems, 21, 1371-1378.
https://doi.org/10.1109/TPWRS.2006.876672 [Paper reference null] - 25. Morales-España, G., Latorre, J.M. and Ramos, A. (2013) Tight and Compact MILP Formulation for the Thermal Unit Commitment Problem. IEEE Transactions on Power Systems, 28, 4897-4908.
https://doi.org/10.1109/TPWRS.2013.2251373 [Paper reference null] - 26. Albalawi, H., Makram, E. and Alogla, T. (2015) PV Penetration with Battery Storage for an Isolated Northwest Grid of Saudi Arabia. North American Power Symposium (NAPS), Charlotte, 4-6 October 2015, 1-6.
https://doi.org/10.1109/naps.2015.7335082 [Paper reference null] - 27. Albalawi, H. and Makram, E. (2015) Power Quality Study of an Isolated Northwest Grid of Saudi Arabia with PV and Storage. Journal of Power and Energy Engineering, 3, 54-64.
https://doi.org/10.4236/jpee.2015.36006 [Paper reference null]
Nomenclature
A. Binary Variables


B. Continuous Variables






C. Parameters













T: Set of all dispatches included in optimization horizon.
Submit or recommend next manuscript to SCIRP and we will provide best service for you:
Accepting pre-submission inquiries through Email, Facebook, LinkedIn, Twitter, etc.
A wide selection of journals (inclusive of 9 subjects, more than 200 journals)
Providing 24-hour high-quality service
User-friendly online submission system
Fair and swift peer-review system
Efficient typesetting and proofreading procedure
Display of the result of downloads and visits, as well as the number of cited articles
Maximum dissemination of your research work
Submit your manuscript at: http://papersubmission.scirp.org/
Or contact jpee@scirp.org







