Journal of Power and Energy Engineering
Vol.04 No.09(2016), Article ID:70535,16 pages
10.4236/jpee.2016.49004
Application of the Weibull Distribution to Estimate the Volume of Water Pumping by a Windmill
M. Toledo Velázquez1, J. Hernández Rodríguez2, M. Vega Del Carmen1*, F. E. Flores Murrieta2, G. Tolentino Eslava1
1Laboratorio de Ingeniería Térmica e Hidráulica Aplicada (LABINTHAP), IPN-SEPI-ESIME Zacatenco, Ciudad de México, México
2División de Ciencias e Ingeniería, Laboratorio en Sistemas de Energía, Universidad de Quintana Roo, Chetumal, México

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: April 29, 2016; Accepted: September 10, 2016; Published: September 13, 2016
ABSTRACT
Given the steady increase in use of alternative energy sources to supply part of the energy demand of the world, and considering that Mexico has enough wind resources to produce all the electricity required by the country, in this work, it is carried out the development of a system of wind resource assessment to determine the volume of water that a windmill pumping system can provide in a specific area. To this end, it has developed a computer program for wind resource assessment by measurements of wind speed, direction, temperature, barometric pressure and relative humidity. Measuring equipments were mounted in a wind measurement tower of 10 m high, within the premises of the University of Quintana Roo which is located along the coast. Until this day, there are records over a period of five months of the variables of wind speed, wind direction, temperature, relative humidity and atmospheric pressure. These variables were used for statistical calculations using the Weibull distributions. To give a better use of the calculated data, they were applied to the evaluation of a Pumping System.
Keywords:
Pumping Systems, Weibull Distribution, Wind Energy, Windmill

1. Introduction
As part of the implementation of wind energy evaluation and application in Mexico, at the University of Quintana Roo, division of Science Engineering Energy Systems Laboratory, is developing a methodology for preliminary evaluation of the wind energy potential, the section is trying to use computer programming in order to obtain a standard methodology that can be applied to rural areas in which the wind energy is considered a potential source to generate mechanical energy to use in pumping systems or electricity generation.
It is necessary to know the wind characteristics to predict the amount of energy that can be extracted by any wind energy converter system as well as proving the feasibility of the system in order to use the wind potential. Monthly and Annual wind distributions can be calculated and plotted from the wind speed data, since they depend on knowing how much energy can be extracted and in what period of time due to the wind aleatory characteristics. It is also necessary to analyze the aerodynamic theories of wind rotors and the pumping machines performances to match them to a wind powered pumping system and achieve to extract the maximum power from the wind in a particular place.
2. Measuring Techniques
The energy yield of a wind turbine can be predicted with statistically validated values of mean wind speed, wind speed distribution and the vertical wind profile. Statistically reliable values required measurements at long periods of time. It is necessary the specification of a reliable value for the long-term mean annual wind speed, for this is required the mean value taken over at least ten years. Measurements taken by oneself over a period of only a few months with simple equipment are not suitable for this purpose.
Wind measurement over a relatively short period of time, for instance one year, offers the possibility of comparing these values with the long-term data measured within the same period of time at the closest location at which the long-term mean value is known. This permits the verification of whether and to what extent the local value deviates from the value ascertained for the larger area.
The wind speed is plotted against time, indications as to the turbulence intensity can be derived from the wind variations. From the point of view of the prudently planning operator, wind measurements having this objective make sense and may even be necessary.
The measurements of wind velocity requires of transducers to convert an electric signal in a velocity reading. These devices are mounted on top of or on side arms of a mast or a tower (Figure 1). The mast height depends on the requirements to be met. If only a comparison with the data in the wind maps is intended, then the standard measuring elevation of 10 m is enough. If there are too many uncertainties concerning to wind shear, it is necessary to build the wind measuring mast as high as the rotor hub height. However, a wind measuring mast with a height equal to or greater than fifty meters represents a cost factor.
In the past, mechanical anemographs were used which plotted wind speed and direction on a paper strip. Mean values were determined with the help of a plotting rule. Nowadays, electronic recorders are used almost exclusively where the measured data is stored on tape or in a chip. This provides for immediate data evaluation by computer.
Figure 1. Anemometric tower with a cup anemometer and vane.
The manufacturers offer an almost endless variety of suitable storage devices and analyzers. Figures 2-6 show the wind data acquisition for a period of 5 months with a period of acquisition of 10 minutes. During the period of time was done a mean of the total data in 10 minutes with 10 reading per second. The data meaning was saved in a memory which include temperature, wind velocity, humidity and density.
3. Parameters k and c
It is quite logical to look for mathematical functions that approach the frequency and duration curves as closely as possible, as a tool to predict the output of windmills later on. In this respect much attention has been given to the Weibull distribution [1] , since it is a good match with the experimental data. The Weibull distribution is characterized by two parameters: the Shape Parameter k (dimensionless) and the Scale Parameter c (m/s). The Weibull distribution uses two functions: The Cumulative Distribution Function F(V), indicating the time fraction or probability that the wind speed V is smaller than or equal to a given wind speed V’, Equation (1).
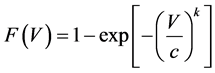 (1)
(1)
The Probability Density Function, represented in this case by the velocity frequency curve given by Equation (2).
 (2)
(2)
The average wind speed can be expressed as a function of c and k or vice versa; c is a function of
Figure 2. January data.
Figure 3. February data.
Figure 4. March data.
Figure 5. April data.
Figure 6. May data.
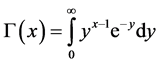 (3)
(3)
With  and
and 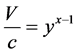 one obtains
one obtains 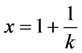 and after a few manipulations results Equation (4).
and after a few manipulations results Equation (4).
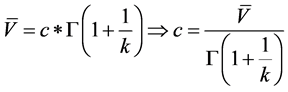 (4)
(4)
F(V) and f(V) yields Equation (5) and Equation (6).
 (5)
(5)
 (6)
(6)
Calling  the reduced wind velocity and represented it by X result Equation (7) and Equation (8).
the reduced wind velocity and represented it by X result Equation (7) and Equation (8).
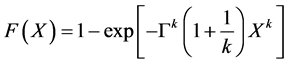 (7)
(7)
 (8)
(8)
4. Estimation of Weibull Parameters from Given Data
The Weibull distribution shows its usefulness when the wind data of one reference place are being used to predict the wind regime in the surrounding of that place. There are some methods to extract the Weibull parameters k and c from a given set of data [2] :
Weibull Paper
Standard Deviation Analysis
Energy Pattern Factor
Empirical Method
Maximum Likelihood Method.
The Maximum Likelihood Method can be programmed, which is very useful to have an automatic process while obtaining the Weibull parameters. The other methods are considered with less accurate than this, one because of their graphical and empirical characteristics. Although they are used as a reference to evaluate the results of the maximum likelihood method gives.
Figure 7 and Figure 8 show the Cumulative Distribution Function and the Probability Density Function respectively for some wind regimes, noting the importance of cal-
Figure 7.The Weibull cumulative distribution function versus the reduced wind velocity for different values of the Weibull shape factor.
Figure 8. The dimensionless Weibull wind speed frequency curve as a function of the reduced wind velocity for different values of the Weibull shape factor.
culating the Weibull distribution Parameters. The F(X) curve (Figure 7) shows the percentage of time that the wind speed will be below the average wind speed during a wind regime (i.e., a given k value).
The f(X) curve (Figure 8) shows the most frequent wind speed value in a given wind regime (i.e., k = any value) versus the average wind speed. It is possible to convert this value to a fraction that indicates the time fraction this most frequent wind speed occurs. Figure 9 shows the wind velocity and power density fluctuations for each month of a year, with the Energy Pattern Factor included in the power density calculations, and so having an idea of a period of year in which the maximum power can be extracted by a wind energy converter system.
5. Wind Rotor Performance
The fraction of extracted power that is called power coefficient Cp, in practice seldom exceeds 40% if measured as the mechanical power of a wind rotor. The subsequent conversion into electrical power or pumping power gives a reduction in available power, depending on the efficiency h of the transmission and pump or generator. A further reduction of the available power is caused by the fluctuations in speed and directions, which an actual windmill experiences in the field.
The design of the rotor consists in reach the next parameters:
Radius
The design tip speed ratio
Number of blades
It is also important to select an adequate airfoil based on a design lift coefficient and the corresponding angle of attack.
Figure 9. Monthly fluctuations of mean wind speed and mean power density for a year in a place of interest.
The radius of the rotor must be calculated with the required energy output E in a year (or in a critical month) given the average local wind speed and its distribution. An approximation for water pumping windmills is given by:

In that way, the energy output E and the radius for a month or for a year can be estimated. The choices of ld and B are more or less related as the guidelines in Table 1 suggest.
The type of load determine ld: water pumping windmills driving piston pumps have 1 < ld < 2 and electricity generating wind turbines usually have 4 < ld < 10.
Figure 10 shows the advantage of having a larger number of blades when the rotor has a low tip speed ratio. This is true for the rotors used by water pumping wind turbines. Note that when the lift to drag ratio is lower than 50, there is a decrease in the performance of the rotor when running at a tip speed ratio higher than 3.
Accordingly, if one wishes to use wind rotors for water pumping which are easy to manufacture and cheap, one might be confined to using simple airfoils shape such as curved plate or flat plates, whose aerodynamics characteristics, this is to say L/D ratio, are low (CL/CD = 10 - 30).
Traditionally single-acting lift pumps have been used in wind powered pumping systems and its characteristics have to be chosen based on the water output requirements at the site.
The design wind speed (Vd) of the system is the wind speed at which the overall efficiency reaches a maximum. This speed can be calculated by realizing that at each wind speed, the net power supplied by the rotor-pump combination must be equal to the hydraulic power to pump the water.
Figure 10. Influence of lift to drag ratio on the maximum power coefficient at each tip speed ratio for an infinite number of blades.
Table 1. Guidelines to choice a number of blades value depending on the tip speed ratio.

The expression given by Equation (10) means that the design wind speed can be modified by changing the stroke of the pump or by installing another size pump. A change in water lifting head also changes the design wind speed. For a first estimation the average local wind speed can be selected as the design wind speed.
6. Wind Powered Pumping Systems
The availability of wind energy is highly variable and is likely to be intermittent. As a rule-of thumb, expect an average of 6 to 8 hours per day of water pumping at a rate specified for a wind velocity of 25 km/h. Hand pumping can be done on some windmill pumps in emergencies, but wind-powered pumping units should be used in conjunction with storage facilities capable of meeting three or four days water demand as a back-up supply during periods of low wind.
If the windmill is used to generate electricity to power an electrically-powered pump, it will probably be necessary to store the electricity in batteries due to the variability in generation. Therefore, a pump powered by an electrical motor for use in conjunction with a windmill that generates electricity should have a Direct Current motor. For such systems, it is important to use good-quality deep-cycle batteries and to incorporate electrical controls such as blocking diodes and charge regulators to protect the batteries.
The positive-displacement cylinder pump is the most common type of pump used in pumping systems using wind turbines. These pumps are connected to a gear box before the wind turbine shaft, Figure 11. The operation of these pumps can be improved with the addition of springs, cams and counterweights that alter the stroke cycle and off-set the weight of the drive rod.
The air-lift pump is an alternative to use the wind energy in pumping systems. The air-lift pump is a type of deep-well pump. This pump is used in dirty water and high viscosity fluids. This pump has no moving parts, other than an air compressor driven by the windmill, and the efficiency of the air compressor is an important factor in determining the overall efficiency of the pump. Compressed air is sent to the well to this boost water to a discharge pipe. It is possible to make water flow calculations for different wind speeds using Equation (11), which includes the volumetric efficiency.

The water flow calculations can be plotted (Figure 14) and compared with the next two empirical expressions. The flow of water pumped over a head of H meter with the hydraulic power Phyd [3] is given by Equation (12).
Figure 11. American windmill pump of 2 m in diameter.

This expression can be reduced to Equation (13).

If a pump is coupled to a wind rotor at a given wind speed such that the mechanical power of the rotor is equal to the mechanical power exerted by the pump. This working point can be found by intersection of the rotor curve and the pump curve. Other expression to calculate the water output per day in a month or in a year period for a given average local wind speed and knowing the rotor diameter, the head and the pump-rotor system efficiency [4] is:

It is possible to use Equation (14) to calculate the water output per day by varying the rotor diameter and using the average wind speed. The rotor-pump system efficiency value can be 12%, which is used for first estimations in wind powered pumping windmills [5] . EPF is the corresponding value to the wind regime (i.e., k value) for the month with the average wind speed. This month can be the critical month. For purposes of first estimations the EPF value is in accordance with a common wind regime (i.e., Rayleigh distribution k = 2; EPF = 1.91) [6] . Reducing the expression by using the above values and to obtain the water flow in litters per hours, Qpd in (l/hr) can be obtained for different rotor diameters and water lifting head by varying the average wind speed.
7. Results
To facilitate the judgment to what extent a given location might be suitable for the utilization of wind energy it is necessary to know the daily, monthly, annual wind pattern, as well as energy produced per month, per year. It is often important to know the number of hours that a windmill will run, then a velocity frequency histogram is obtained for the month of May (Figure 12) or the time fraction that a windmill produces more than given power. The result is the Duration Distribution.
If the histogram is approximated by a smooth curve through the value at the middle of each interval then a Duration Curve results (Figure 13). By studying the shape of this duration curve an idea is obtained about the kind of wind regime. The flatter the duration curve, i.e., the longer one specific wind speed persists, the more constant the wind regime is. The steeper the duration curve, more irregular the wind regime is.
By applying Equations (11) - (14) the average water flow in (litter/hr) is obtained and it is possible to compare the results in order to have different first estimation methods to know if a place has potential for the application of wind powered water pumping systems. Figure 14 shows the curves as a comparison example between the results
Figure 12. The velocity frequency histogram for the month of May in Quintana Roo, México.
Figure 13. The duration distribution for the month of May in Quintana Roo, México.
Figure 14. Comparison example for the water output using Equations (11) - (14) with a given rotor diameter and water lifting head.
from Equations (11) - (14) for a 2.2 m rotor diameter and a 10 m water lifting head.
The efficient extraction of power from the wind is governed not only by the performance of the wind rotor but also the wind behaviour and the response of the entire system [7] - [9] , the load included, to variations in the wind speed (Figure 15). The selection criteria is to select the month with the lower wind speed such a way that with any higher wind speed the system will meet the requirements of the place. For Equation (9), the period T value must be equal to the number of hours contained in the critical month.
From Equations (11) - (14) and the duration distribution, it is possible to calculate the rate of water that a pump can rise in a height of 10 m, considering that the diameter of the windmill was 2 m. Table 2 shows the calculations for the power and volume of water per month.
Table 2 shows that the most common wind velocities along the month of May were the low velocities, and the best power coefficients are for the high velocities. Although, the low velocities had had the better duration in the month, and the high velocities had had the best power coefficients, the better values of volume of water pumped were for the intermediate values of velocities. In fact, the mean of pumping water was 15 m3 per day.
Figure 15. Variation of wind power, wind velocity frequency distribution and the wind energy distribution for a particular location.
Table 2. Calculation for the month of May.
8. Conclusions
The methodology used to analyze the wind data allows establishing a preliminary evaluation over the whole country. However, it depends on availability of wind data. It is therefore possible to know the possibility of eolian utilization performing a previous technical study in order to know the resource potential. With the results obtained, it is possible to compare the rotor geometric characteristics obtained for specific water con- sumption with other machines existing in the market in order to determine its feasibility.
The theoretical approach for the description of the performance of water pumping windmills could be a powerful tool for the selection and design of equipment, together with its use for making realistic estimates of a wind powered lift pump when coupled to a particular wind regime. Another advantage of this work is that it is possible to develop economic feasibility studies about the technology for aerial machine implementation in a given location. These studies must be based on exhaustive resource measurements, necessary to consolidate an eolian project.
Cite this paper
Velázquez, M.T., Rodríguez, J.H., Carmen, M.V.D., Murrieta, F.E.F. and Eslava, G.T. (2016) Application of the Weibull Distribution to Estimate the Volume of Water Pumping by a Windmill. Journal of Power and Energy Engineering, 4, 36-51. http://dx.doi.org/10.4236/jpee.2016.49004
References
- 1. Justus, C.G., Hargraves, W.R., Mikhail, A. and Graber, D. (1977) Methods for Estimating Wind Speed Frequency Distributions. School of Aerospace Engineers, Georgia Institute of Technology, Atlanta.
- 2. Lysen, E.H. (1983) Introduction to Wind Energy CWD 82-1. Amerfoorst, The Netherlands.
- 3. Robert, F., et al. (2012) Taller Sobre Aplicaciones Productivas de la Energía Eólica y la Energía Fotovoltaica. Institute of International Education, Sandia National Laboratory, and Quintana Roo, México Government, Sponsored by US Agency for International Development and the US Energy Department.
- 4. Pinilla, A.E. (1985) Wind Powered Pumping Systems for Colombia. Thesis of Doctor of Philosophy, University of Reading, UK.
- 5. Fingersh, L., Hand, M. and Laxson, A. (2006) Wind Turbine Design Cost and Scaling Model. Technical Report NREL/TP-500-40566, EUA.
- 6. Maki, K., Sbragio, R. and Vlahopoulos, N. (2012) System Design of a Wind Turbine Using a Multi-Level Optimization Approach. Renewable Energy, 43, 101-110.
http://dx.doi.org/10.1016/j.renene.2011.11.027 - 7. Lugo, L.R., Barrera, C.E. and Reyes, A.I. (1990) Methodology for Preliminary Evaluation of the Eolian Potential Case Mexico. Solar and Wind Technology, 7, 527-530.
- 8. Malhotra, P., Hyers, R.W., Manwell, J.F. and McGowan, J.G. (2012) A Review and Design Study of Blade Testing Systems for Utility-Scale Wind Turbines. Renewable and Sustainable Energy Reviews, 16, 284-292.
http://dx.doi.org/10.1016/j.rser.2011.07.154 - 9. Spera David, A. (1995) Wind Turbine Technology, Fundamental Concepts of Wind Turbine Engineering. Department of Energy USA, NASA, ASME Press, New York.
Nomenclature
F(V) Cumulative Distribution Function [--]
f(V) Probability Density Function [s/m]
G(x) Gamma Function [--]
k Weibull Shape Factor [--]
c Weibull Scale Factor [m/s]
V Wind Speed [m/s]

Vd Design Wind Speed [m/s]
F(X) Reduced Cumulative Distribution Function [--]
f(X) Reduced Probability Density Function [--]
X Reduced Wind Velocity [--]
Phyd Hydraulic Power [W]
Pmech Mechanical Power [W]
A Rotor Area [m2]
ra Air Density = 1.225 [kg/m3]
rw Water Density = 1000 [kg/m3]
s Stroke (pump) [m]
Dp Pump Diameter [m]
Cpmax Maximum Power Coefficient [--]
Q Water Flow [m3/s]
Qpd Water Output per Day [m3/day]
g Gravitational Acceleration = 9.81 [m/s2]
H Total Dynamic Load (Head) [m]
R Rotor Radius [m]
l Tip Speed Ratio [--]
ld Design Tip Speed Ratio [--]
B Number of Blades [--]
E Energy Output [W-hr]
T Period Length [hr]
hrp Rotor-Pump System Efficiency [--]
hvol Volumetric Efficiency [--]
hmech Mechanical Efficiency [--]
D Rotor Diameter [m]

















