Journal of Power and Energy Engineering
Vol.03 No.11(2015), Article ID:61420,10 pages
10.4236/jpee.2015.311004
Bidding Strategy in Deregulated Power Market Using Differential Evolution Algorithm
Veera Venkata Sudhakar Angatha1, Karri Chandram2, Askani Jaya Laxmi3
1EEE Department, SR Engineering College, Warangal, India
2Department of EEE & Instrumentation, BITS PilaniKK Birla Goa Campus, Goa, India
3EEE Department, JNTUCE, JNTUH, Hyderabad, India

Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).


Received 28 August 2015; accepted 21 November 2015; published 24 November 2015

ABSTRACT
The primary objective of this research article is to introduce Differential Evolution (DE) algorithm for solving bidding strategy in deregulated power market. Suppliers (GENCOs) and consumers (DISCOs) participate in the bidding process in order to maximize the profit of suppliers and benefits of the consumers. Each supplier bids strategically by choosing the bidding coefficients to counter the competitors bidding strategy. Electricity or electric power is traded through bidding in the power exchange. GENCOs sell energy to power exchange and in turn ancillary services to Independent System Operator (ISO). In this paper, Differential Evolution algorithm is proposed for solving bidding strategy problem in operation of power system under deregulated environment. An IEEE 30 bus system with six generators and two large consumers is employed to demonstrate the proposed technique. The results show the adaptability of the proposed method compared with Particle Swarm Optimization (PSO), Genetic Algorithm (GA) and Monte Carlo simulation in terms of Market Clearing Price (MCP).
Keywords:
Bidding Strategy, Differential Evolution, Power market, Market Clearing Price

1. Introduction
The electric power industry worldwide is experiencing restructuring and deregulation of power market. Deregulation and restructuring of electric power industry around the world raises many challenging issues related to the operation of power system. The core issue of restructuring is deregulating the power industry and introducing the competition among the generating companies. Competition creates the opportunities for GENCOs to get more profit. In restructured power market, each GENCO reasonably builds strategic bid to maximize its own profit [1] [2] . The market efficiency is improved with the deregulated power market structure. The power exchange and ISO are independent non-profit organizations. Electricity is traded through bidding in the power exchange (PX). ISO controls and operates the transmission grid. GENCOs sell energy to PX and ancillary services to ISO. Energy is distributed to end users through distribution network and ancillary services are used to support the system organization. A framework for sub-optimal bidding strategy was presented in [3] . Genetic algorithm [4] [5] has been proposed for solving bidding strategy. A two level optimization algorithm was adopted in [6] for building market bidding strategy, where the market participants try to maximize their profit. A brief literature survey on bidding strategy is presented in [7] . Several classical techniques such as Markov decision process [8] [9] , Lagrangian Relaxation [10] , Monte Carlo based approach [11] have been proposed by various scholars in the past decade. Apart from these methods, few other techniques [12] -[21] are suggested to solve the bidding strategy. Recently, modern heuristic methods [22] -[32] like particle swarm optimization, gravitational search algorithm and hybrid algorithms have been proposed to solve the bidding strategy problem with wide variety.
It is noticed from the literature survey that several techniques are adopted to solve strategic bidding problem. However, there is a need to improve the quality of solution in terms of profit. The main objective of this paper is to suggest a new technique for solving bidding strategy problem. Therefore, DE is recommended in this paper. The remaining paper is formulated as follows: problem formulation for bidding in Section II; proposed methodology and implementation steps of DE in Section III; case studies in Section IV; conclusions of the paper in Section V.
2. Problem Formulation for Bidding
Consider a power system consists of “n” independent generators, an inter-connected transmission network controlled by ISO, a Power Exchange, an aggregated load, and “m” large consumers who join in demand side bidding. Further, assume that every generating company and large consumer is required to bid a linear non-de- creasing supply and non-increasing demand functions respectively to power exchange.
The GENCO supply bid price is denoted by 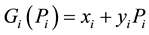 where
where ,
,  is the ith generator active power output,
is the ith generator active power output,  is intercept and
is intercept and 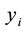 is slope of the supply bid curve. The jth large consumer demand price is denoted by
is slope of the supply bid curve. The jth large consumer demand price is denoted by 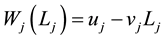 where
where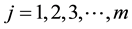 ,
, 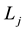 is the jth load active power demand.
is the jth load active power demand. 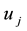 is intercept and
is intercept and 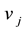 is slope of the demand bid curve.
is slope of the demand bid curve.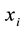 ,
, 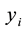 ,
, 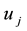 , and
, and 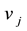 are non-negative bidding coefficients.
are non-negative bidding coefficients.
Now, the main task of Power Exchange is to determine a set generation outputs, a set of consumer demands that minimizes the total purchasing cost, while meeting the security and reliability constraints with clear dispatch procedures. That is, Power Exchange determines a set of power outputs 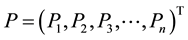 and a set of demands
and a set of demands 


Power balance equation is as follows:

where, MCP is the electricity uniform market clearing price to be determined. 
Generation and load in equality constraints are:


where 




where
When the generation and load inequality constraints are neglected, the solution to equations are as follows:

Power awarded to generator and large consumer is calculated as follows:


When solution of Equations (8) violates the maximum power limit








Subject to Equations (1)-(5) where Ci (Pi) is ith supplier production cost function. The generation cost function is expressed as follows:

where fi, ei, and di are fuel cost coefficients of ith generator. The marginal cost of ith generator is calculated as follows:

The objective is to determine 



Subject to Equations (1)-(5) where 



It is known that bidding participants can set MCP at the level that ensures maximum profit to them if they aware bidding strategy of rivals. Whereas in sealed bid auction based market, electricity data for the next bidding period is not openly available, hence GENCOs and large consumers cannot solve the problem due the information needed to solve the problem given in Equations (10) and (13) is not available. But, the bidding previous history is available, and hence the bidding coefficients of opponents can be roughly calculated. However, previous round bidding information will be made open to all participants, after market operator decides MCP, and market participants can make use of this information to develop their strategic bids for the next round of transaction. Whereas, each supplier can estimate their opponents bidding coefficients using probability distribution function (pdf).
3. Proposed Methodology
In this section, a brief description of DE [33] and the implementation steps of DE for bidding strategy are provided.
3.1. Differential Evolution
Differential Evolution algorithm [34] has been proposed by Storn and Price in 1995. It is a basic yet effective population-based stochastic search procedure for taking care of global optimization problems. The algorithm is named as Differential Evolution because of a unique kind of differential operator, which makes new off-springs from parent chromosomes rather than classical crossover and mutation.
A brief depiction about different operators of differential evolution is given beneath:
3.1.1. Initialization
First step of DE is initialization of population. The population should cover the whole search space. The upper and lower limits are taken as Xmax and Xmin:


where D represents number of variables. The jth component of the ith individual is initialized as follows:

where 

3.1.2. Mutation
Off springs for the next generation are introduced into the population through transformation process. The transformation is performed by selecting three individuals from the populace in an arbitrary way.
Let Xr1, Xr2, Xr3 and Xi represent three random individuals and target individual respectively such that r1 ≠ r2 ≠ r3 ≠ i upon which mutation is performed during the Gth generation as:

where Vi,G+1 is the perturbed mutated individual. The difference of two random individuals is scaled by an element F, which controls the amplification of the contrast between two individuals in order to avoid search stagnation and to enhance convergence.
3.1.3. Crossover
New off-springs are reproduced through the crossover operation based on binomial distribution. The members of the current population (target individual) and the members of the mutated individuals are subjected to crossover operation in this manner delivering a trial vector as follows:

where Cr is the crossover constant that controls the diversity of the population and prevents the algorithm from getting caught into the local optima. The crossover constant must be in the range of [0,1]. Cr = 1 infers the trial vector will be composed entirely of the mutant vector individuals and Cr = 0 infers that the trial vector members are composed of the individuals of parent vector. The mathematical statement can also be written as:

3.1.4. Selection
In DE, selection technique is performed with the trial vector and the objective vector to get the best set of people for the next generation. In the proposed methodology, one and only population kept up and consequently the best individuals replace the object individual’s in the present population. The objective values of the trial vector and the object vector obtained from the fitness function are evaluated and compared.

Mutation, crossover and selection continue until some stopping criterion is reached.
Flowchart of Differential Evolution is shown in Figure 1.
3.2. Differential Evolution for Bidding Strategy
Complete procedure of the differential evolution algorithm for solving bidding strategy is illustrated below (Figure 2):
1) Step I Input Data
(i) For Bidding problem: Number of suppliers, number of consumers, fuel cost data of suppliers and consumers. (ii) For Differential evolution: Population size, number of iterations, mutation and crossover ratio.
2) Step II Initialization
Initialization is one of the important steps in solving the bidding strategy problem. Thebidding coefficients are inter-dependent. Here, x and u are kept constant and y and v are selected randomly.
3) Step III Iterations Starts
(i) Calculate Market Clearing Price
(ii) Evaluate powers of suppliers and large consumers
(iii) Calculate profit of suppliers and large consumers.
4) Step IV Iterations Starts for DE
(i) Generate donors by mutation
(ii) Perform recombination
(iii) Evaluate MCP for updated values of b and d
(iv)Evaluate powers and check for limits of generators and consumers
(v) Check the error
(vi) Find the best solution
(vii) End of iterations for DE
(viii) End of iterations
5) Step V Final Results
4. Case Studies
The proposed DE algorithm is tested on a IEEE 30 bus system with six generators and two consumers. Coding of the algorithm is developed in MATLAB (version 2012 A) and executed in personal laptop (Dell vostro, i3,2310 M CPU 2.10 Ghz, 4GB RAM, 64 bit WINDOW operating system). Fuel cost coefficients of generators
Figure 1. Flowchart of differential evolution.
(e in $/MWh, and f in $/MW2h), demand cost coefficients (g and h), generator output power limits and large consumer load demands are taken from [31] and are provided in Table 1.
During execution of the proposed algorithm, the numerical values of various control parameters are used and are shown in Table 2.
Each rival supplier is assumed to have an estimated joint normal distribution for the bidding coefficients.
Figure 2. Flowchart of proposed method.
Table 1. Generator and large consumer data.
After execution of the proposed algorithm, the end results of a and b are listed in Table 3. The market clearing price (MCP) by the proposed algorithm is 17.6405 $/MWh.
The powers of generators and consumers are given in Table 4. The estimated profit of six generators and benefit of two large consumers are shown in Table 5.
Market clearing price of different methods, which decides the profit of the bids, is given in Figure 3.
The estimated total profit of six generators and two large consumers with different methods are shown in Figure 4. The sum of profit obtained both for generators and consumers by the proposed method is $5076.70, which is higher than the profit obtained from PSO, GA and Monte Carlo methods.
Table 2. Numerical values of various control parameters.
Table 3. Bidding coefficients of generators and large consumers.
Table 4. Comparison of Generated Powers in MWs with different methods.
Figure 3. Comparison of Market Clearing Price (MCP) with different methods.
Figure 4. Comparison of Profits with different methods.
Table 5. Comparison of Benefits ($) with different methods.
5. Conclusion
Differential evolution for solving bidding strategy in deregulated power market is presented in this paper. The proposed algorithm is an effective method and easy to implement for solving bidding strategy problem. From the reported results it is observed that the proposed differential evolution is an effective method in terms of quality of solution. The simulation results show that the proposed differential evolution algorithm provides better solution in terms of profit compared to the existing methods available in the literature survey. More realistic strategic bidding problem can be developed for generating companies and consumers for better competition in the real time operation of power system under deregulation.
Cite this paper
Veera VenkataSudhakar Angatha,KarriChandram,Askani JayaLaxmi, (2015) Bidding Strategy in Deregulated Power Market Using Differential Evolution Algorithm. Journal of Power and Energy Engineering,03,37-46. doi: 10.4236/jpee.2015.311004
References
- 1. Lai, L.L. (2001) Power System Restructuring and Deregulation-Trading, Performance and Information Technology. Wiley, New York.
http://dx.doi.org/10.1002/0470846119 - 2. Shahidepour, M., Yamin, H. and Li, Z. (2002) Market Operations in Electric Power Systems: Forecasting, Scheduling and Risk Management. Wiley, New York.
- 3. Lamont, J.W. and Raman, S. (1997) Strategic Bidding in an Energy Brokerage. IEEE Transactions on Power Systems, 12, 1729-1733.
http://dx.doi.org/10.1109/59.627883 - 4. Richter Jr., C.W. and Shible, G.B. (1998) Genetic Algorithm Evolution of Utility Bidding Strategies for the Competitive Marketplace. IEEE Transactions on Power Systems, 13, 256-261.
http://dx.doi.org/10.1109/59.651644 - 5. Richter Jr., C.W., Shible, G.B. and Ashlock, D. (1998) Comprehensive Bidding Strategies with Genetic Programming: Finite State Automata. IEEE Transactions on Power Systems, 14, 1207-1212.
http://dx.doi.org/10.1109/59.801874 - 6. Weber, J. and Overbye, T. (1999) A Two-Level Optimization Problem for Analysis of Market Bidding Strategies. IEEE PES Summer Meeting, 2, 682-687.
- 7. David, A.K. and Wen, F. (2000) Strategic Bidding in Competitive Electricity Markets: A Literature Survey. IEEE Power Engineering Society Summer Meeting, 4, 2168-2173.
- 8. Hao, S. (2000) A Study of Basic Bidding Strategy in Clearing Pricing Auctions. IEEE Transactions on Power Systems, 15, 975-980.
http://dx.doi.org/10.1109/59.871721 - 9. Song, H., Liu, C.-C., Lawarree, J. and Dahlgren, R.W. (2000) Optimal Electricity Supply Bidding by Markov Decision Process. IEEE Transactions on Power Systems, 15, 618-624.
http://dx.doi.org/10.1109/59.867150 - 10. Zhang D., Wang, Y. and Luh, P.B. (2000) Optimization Based Bidding Strategies in the Deregulated Market. IEEE Transactions on Power Systems, 15, 981-986.
http://dx.doi.org/10.1109/59.871722 - 11. Wen, F.S. and David, A.K. (2001) Optimal Bidding Strategies and Modeling of Imperfect Information among Competitive Generators. IEEE Transactions on Power Systems, 16, 15-21.
http://dx.doi.org/10.1109/59.910776 - 12. Wen, F.S. and David, A.K. (2001) Optimal Bidding Strategies for Competitive Generators and Large Consumers. Electrical Power and Energy Systems, 23, 37-43.
http://dx.doi.org/10.1016/S0142-0615(00)00032-6 - 13. Wen, F.S. and David, A.K. (2001) Strategic Bidding for Electricity Supply in a Day-Ahead Energy Market. Electric Power Systems Research, 59, 197-206.
http://dx.doi.org/10.1016/S0378-7796(01)00154-7 - 14. Guan, X., Ho, Y.-C. and Lai, F. (2001) An Ordinal Optimization Based Bidding Strategy for Electric Power Suppliers in the Daily Energy Market. IEEE Transactions on Power Systems, 16, 788-797.
http://dx.doi.org/10.1109/59.962428 - 15. David, A.K. (2002) Competitive Bidding in Electricity Supply. IEE Proceedings on Generation, Transmission and Distribution, 140, 421-426.
http://dx.doi.org/10.1049/ip-c.1993.0061 - 16. Gountis, V.P. and Bakirtzis, A.G. (2004) Bidding Strategies for Electricity Producers in a Competitive Electricity Market Place. IEEE Transactions on Power Systems, 19, 356-365.
http://dx.doi.org/10.1109/TPWRS.2003.821474 - 17. Li, T. and Shahidehpour, M. (2005) Strategic Bidding of Transmission-Constrained GENCOs with Incomplete Information. IEEE Transactions on Power Systems, 20, 437-447.
http://dx.doi.org/10.1109/TPWRS.2004.840378 - 18. Ma, X., Wen, F., Ni, Y. and Liu, J. (2005) Towards the Development of Risk-Constrained Optimal Bidding Strategies for Generation Companies in Electricity Markets. Electric Power Systems Research, 73, 305-312.
http://dx.doi.org/10.1016/j.epsr.2004.07.004 - 19. Attaviririyanupap, P., Kita, H., Tanaka, E. and Hasegawa, J. (2005) New Bidding Strategy Formulation for Day-Ahead Energy and Reserve Markets Based on Evolutionary Programming. Electrical Power and Energy Systems, 27, 157-167.
http://dx.doi.org/10.1016/j.ijepes.2004.09.005 - 20. Rahimiyan, M. and Mashhadi, H.R. (2008) Supplier’s Optimal Bidding Strategy in Electricity Pay-as-Bid Auction: Comparison of the Q-Learning and a Model Based Approach. Electric Power Systems Research, 78, 165-175.
http://dx.doi.org/10.1016/j.epsr.2007.01.009 - 21. Boonchuay, C., Ongsakul, W., Zhong, J. and Wu, F.F. (2010) Optimal Trading Strategy for GenCo in LMP-Based and Bilateral Markets Using Self-Organising Hierarchical PSO. International Journal of Engineering, Science and Technology, 2, 82-93.
- 22. Soleymani, S. (2011) Bidding Strategy of Generation Companies Using PSO Combined with SA Method in the Pay as Bid Markets. Electrical Power and Energy Systems, 33, 1272-1278.
http://dx.doi.org/10.1016/j.ijepes.2011.05.003 - 23. Azadeh, A., Ghaderi, S.F., Nokhandan, B.P. and Sheikhalishahi, M. (2012) A New Genetic Algorithm Approach for Optimizing Bidding Strategy Viewpoint of Profit Maximization of a Generation Company. Expert System with Applications, 39, 1565-1574.
http://dx.doi.org/10.1016/j.eswa.2011.05.015 - 24. Kumar, J.V., Kumar, D.M.V. and Edukondalu, K. (2013) Strategic Bidding Using Fuzzy Adaptive Gravitational Search Algorithm in a Pool Based Electricity Market. Applied Soft Computing, 13, 2445-2455.
http://dx.doi.org/10.1016/j.asoc.2012.12.003 - 25. Qiu, Z., Gui, N. and Decininck, G. (2013) Analysis of Equilibrium-Oriented Bidding Strategies with Inaccurate Electricity Market Models. Electrical Power and Energy Systems, 46, 306-314.
http://dx.doi.org/10.1016/j.ijepes.2012.10.036 - 26. Wen, F.S. and David, A.K. (2000) Coordination of Bidding Strategies in Energy and Spinning Reserve Markets for Competitive Suppliers Using Genetic Algorithm. Power Engineering Society Summer Meeting, Vol. 4, Seattle, 16-20 July 2000, 2174-2179.
http://dx.doi.org/10.1109/PESS.2000.866983 - 27. Wen, F.S. and David, A.K. (2001) Strategic Bidding for Electricity Supply in a Day-Ahead Energy Market. Electrical Power Systems Research, 59, 197-206.
http://dx.doi.org/10.1016/S0378-7796(01)00154-7 - 28. Wen, F.S. and David, A.K. (2002) Coordination of Bidding Strategies in Day-Ahead Energy and Spinning Reserve Markets. Electrical Power and Energy Systems, 24, 251-261.
http://dx.doi.org/10.1016/S0142-0615(01)00038-2 - 29. Wen, F.S. and David, A.K. (2002) Optimally Co-Ordinated Bidding Strategies in Energy and Ancillary Service Markets. IEE Proceedings on Generation, Transmission and Distribution, 149, 331-338.
http://dx.doi.org/10.1049/ip-gtd:20020211 - 30. Yang, L, Wen, F., Wu, F.F., Ni, Y. and Qiu, J. (2002) Development of Bidding Strategies in Electricity Markets Using Possibility Theory. IEEE International Conference on Power System Technology, 1, 182-187.
http://dx.doi.org/10.1109/ICPST.2002.1053529 - 31. Kumar, J.V., Pasha, S.J. and Kumar, D.M.V. (2010) Strategic Bidding in Deregulated Market Using Particle Swarm Optimization. Annual IEEE India Conference, Kolkata, 17-19 December 2010, 1-6.
http://dx.doi.org/10.1109/indcon.2010.5712648 - 32. Zhang, G., Zhang, G.L., Gao, Y. and Lu, J. (2011) Competitive Strategic Bidding Optimization in Electricity Markets Using Bilevel Programming and Swarm Technique. IEEE Transactions on Industrial Electronics, 58, 2138-2146.
http://dx.doi.org/10.1109/TIE.2010.2055770 - 33. Sudhakar, A.V.V., Chandran, K. and Laxmi, A.J. (2014) Differential Evolution for Solving Multi Area Economic Dispatch. International Conference on Advances in Computing, Communications and Informatics (ICACCI), New Delhi, 24-27 September 2014, 1146-1151.
http://dx.doi.org/10.1109/ICACCI.2014.6968486 - 34. Storn, R. and Price, K. (1997) Differential Evolution—A Simple and Efficient Heuristic for Global Optimization over Continuous Spaces. Journal of Global Optimization, 11, 341-359.
http://dx.doi.org/10.1023/A:1008202821328






