Journal of Power and Energy Engineering
Vol.02 No.10(2014), Article ID:50386,5 pages
10.4236/jpee.2014.210004
Simultaneous One-Step Approximations of Real and Reactive Power Flow*
Arie Ten Cate
Retired, Berkel en Rodenrijs, The Netherlands
Email: arietencate@gmail.com
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 17 July 2014; revised 25 August 2014; accepted 14 September 2014
ABSTRACT
This paper presents two new non-iterative approximations of the power flow in a network. Real and reactive power are simultaneously modelled in complex equations. Also, resistances are not set to zero. This is a generalization of the DC approximation, where only real power is modelled with zero line resistance. Hence the proposed approximations are more accurate than the DC approximation. The voltage lag over a link in a short, low voltage, network link is ten times as accurate as with the DC approximation. In the Appendix a new mathematical constant is introduced.
Keywords:
Power Flow Modeling, Non-Iterative Modeling, Taylor Expansion, Taylor Approximation, DC Approximation

1. Introduction
For AC network power flow calculations there are two widely used models: the exact AC model and the DC linear approximation. Being linear, the DC model solves in one step; it is used when this advantage outweighs the disadvantage of being approximate. See [2] -[5] .
The DC approximation is based on several assumptions. However, one of these assumptions is not needed to obtain a linear system: the assumption of negligible line resistances. A linear system without this assumption is more accurate, in particular of course if this assumption is far from satisfied. Also, the DC approximation models only real power.
The rest of the paper is organized as follows. We start with the exact AC model in Section 2. In Section 3 the linear Taylor approximation is applied. This results in two quite similar models. Then we add the unneeded assumption, arriving at a cruder model, of which the DC model is a part. The estimation of the line losses is discussed shortly in Section 4. In Section 5 the accuracies of the linear models are computed using a simple example. Finally some conclusions are given and in the Appendix a mathematical detail is discussed.
2. The Exact Model
Consider a power network to which applies the standard Short Line model; i.e., without shunt capacitances. We have for the voltages at the ends of a link between node 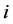 and node
and node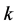 :
:
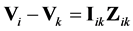 (1)
(1)
with 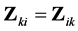 and hence
and hence . Complex variables are bold upright (except in the Appendix).
. Complex variables are bold upright (except in the Appendix).
Then the conjugate complex power flow from node  in the direction of node
in the direction of node 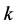 is given by:
is given by:
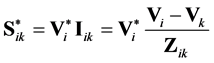 . (2)
. (2)
Substituting this into the equations stating that the net power flow from any network node is zero, gives the well-known simultaneous nonlinear system of equations, with as many equations as unknown node voltages. (At a node with a generator, we have a given voltage and a unknown power supply from the generator.)
After solving this system for the voltages, the currents can be computed using (1).
3. The Linear Taylor Models
The standard method for the linearization of a function is the first-order Taylor approximation. This will be applied here with complex differentiation, using a lemma about the derivative of a conjugate. The same result can be obtained without this lemma, differentiating with respect to the real and imaginary parts of the voltages. Finally, a slightly different result is obtained when differentiating with respect to the polar coordinates of the voltages.
3.1. Complex Differentiation
Rewrite (2) as
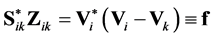 . (3)
. (3)
We shall alternatively consider 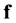 as a function of the complex
as a function of the complex 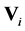 and
and 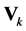 themselves, or as a function of the rectangular or the polar coordinates of the complex voltages.
themselves, or as a function of the rectangular or the polar coordinates of the complex voltages.
Consider the first order Taylor approximation of 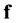 around the point defined by
around the point defined by
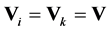 (4)
(4)
where 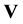 is a given voltage, such as the nominal voltage, usually chosen to be real. It is assumed that all voltages in the network are close to this point. At this point we have
is a given voltage, such as the nominal voltage, usually chosen to be real. It is assumed that all voltages in the network are close to this point. At this point we have .
.
The two derivatives at (4) are:

For the second equality sign in the first derivative, see the Appendix. Then we have the following Taylor expansion around (4):

The total system is now linear in all nodal voltages. This boils down to replacing the 

3.2. Scalar Differentiation: Cartesian Coordinates
The above result can also be obtained without the Appendix, by differentiating with respect to the real and imaginary parts of the voltages, as follows.
Let 



The four derivatives at (4) are:

Then we have the following Taylor expansion around (4):

This is the same result as (6) above.
3.3. Scalar Differentiation: Polar Coordinates
Instead of the cartesian coordinates, we might express the complex voltages in their magnitude and their argument (phase angle). Then, instead of point (4), we now have:

with given 




Rewrite 


The three derivatives at (10) are:

Then we have the following Taylor expansion around (10):

with

the voltage magnitude drop. Hence we have:

This result differs from the above linearization.
We have here a generalization of Equations (48) and (49) of [1] . The generalization is our complex given voltage



Using 

which is equal to (15) with 

3.4. The DC Approximation
Adding the assumption of negligible line resistances changes 


This is the well known DC approximation, modelling only real power and ignoring line resistance. There is little to recommend this, compared with the other linear approximations above.
Probably these two reductions (no 

4. Line Losses
With each of the above linear approximations, the power flow from 




5. Example
One would expect the two Taylor approximations to be more accurate than the DC approximation. This is indeed the case in the example presented in Table 1, modelling one single-phase low-voltage network link at the end of a line in a residential area. The parameters, shown at the foot of the table, are taken from Appendix F.6 of [1] with a small change of the sending end voltage. The magnitude of this voltage is below the nominal voltage, due to the voltage drop from the generator down to this link.
The errors with polar Taylor are easy to explain from (15): the 


With the DC, the voltage lag error is more than ten times larger than with the two Taylor models. A similar result is found in the forthcoming [6] , where the polar Taylor is investigated.
6. Conclusions
Two new non-iterative approximations of the power flow over a short transmission line have been introduced, based on the general method for linear approximations: the first-order Taylor approximation. The equations of
Table 1. The voltage change over a link in a low-voltage network.

these approximations are complex, modelling in this way both real and reactive power.
They result from the same assumptions as the DC approximation, except the needless assumption of small 
A simple example shows what one might expect from this model: much more accurate voltages than the DC approximation. There seems to be little motive to use the DC approximation.
Further work is needed to test this with larger applications (as in [6] ) and to extend this approach to the Medium-Length Line model (i.e., including shunt capacitances).
References
- Ten Cate, A. (2012) The Socially Optimal Energy Transition in a Residential Neighbourhood in the Netherlands. http://www.cpb.nl
- Purchala, K., Meeus, L., Van Dommelen, D. and Belmans, R. (2005) Usefulness of DC Power Flow for Active Power Flow Analysis. IEEE Power Engineering Society General Meeting, 1, 454-459.
- Van Hertem, D., Verboomen, J., Purchala, K., Belmans, R. and Kling, W.L. (2006) Usefulness of DC Power Flow for Active Power Flow Analysis with Flow Controlling Devices. The 8th IEE International Conference on AC and DC Power Transmission, 28-31 March 2006, 58-62. http://dx.doi.org/10.1049/cp:20060013
- Stott, B., Jardim, J. and Alsaç, O. (2009) DC Power Flow Revisited. IEEE Transactions on Power Systems, 24, 1290- 1300. http://dx.doi.org/10.1109/TPWRS.2009.2021235
- Coffrin, C., Van Hentenryck, P. and Bent, R. (2012) Approximating Line Losses and Apparent Power in AC Power Flow Linearizations. IEEE Power and Energy Society General Meeting, San Diego, 22-26 July 2012, 1-8.
- Pouw, J.I.P. (2014) Capacity Evaluation of Medium Voltage Distribution Network Planning Alternatives. M.Sc. Thesis, Eindhoven University of Technology, Eindhoven.
Appendix. The Magnitude of
A complex-valued function 


The complex derivative of the conjugate is

with




However, we have:

Hence, although one might say that 



Compare with Complex Infinity (loosely speaking, a complex number with infinite magnitude but without argument) and with Complex Zero (a complex number with zero magnitude and without argument).
A practical use of this result is as follows: for any real or complex 

and in particular:

and hence also:

This last result is used in section 3.1, Equation (5).
NOTES
*Rob Aalbers (CPB) suggested the use of Taylor while I was working on [1] .




