Journal of Power and Energy Engineering
Vol.2 No.1(2014), Article ID:42166,8 pages DOI:10.4236/jpee.2014.21004
Design Analysis of DC-DC Converters Connected to a Photovoltaic Generator and Controlled by MPPT for Optimal Energy Transfer throughout a Clear Day
1Department of Electronics, Sfax High Institute of Electronics and Communications, University of Sfax, Sfax, Tunisia; 2Electronic Laboratory and Information Technology, Department of Electrical Engineering, Sfax National School of Engineers, University of Sfax, Sfax, Tunisia; 3Department of Physics, Science Faculty of Sfax, University of Sfax, Sfax, Tunisia.
Email: *sami.kolsi@gmail.com
Copyright © 2014 S. Kolsi et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. In accordance of the Creative Commons Attribution License all Copyrights © 2014 are reserved for SCIRP and the owner of the intellectual property S. Kolsi et al. All Copyright © 2014 are guarded by law and by SCIRP as a guardian.
Received Nov 30th, 2013; revised Dec 5th, 2013; accepted Dec 20th, 2013
Keywords:DC-DC Converter; Energy Efficiency; Design; Load Matching; MPPT
ABSTRACT
The DC-DC converters are widely used in photovoltaic generating systems as an interface between PV module and the load. These converters must be chosen to be able to match the maximum power point (MPP) of PV module when climatic conditions change with different resistive load values. So DC-DC converters must be used with MPPT controller in order to reduce losses in the global PV system. This article focuses on the effect of climatic conditions on design of two components (inductance, capacitance) for three topologies of DC-DC converters commonly used in PV systems. When climatic conditions change, the boundary of inductance and capacitance parameters of DC-DC converter will change. These two parameters must be properly sized to achieve optimal efficiency for each converter. The design optimization is based on two principles: 1) for a steady-state operation in a continuous conduction mode, the inductance value for all choppers must be greater than the maximum value of boundary inductance, and 2) in order to limit the output voltage ripple of DC-DC converter below a desired value, the filter capacitance must be larger than the maximum value of boundary capacitance.
1. Introduction
When a PV module is directly coupled to a given load resistance RLA (Figure 1), the operating point is located at A. For another value of resistive load RLB, the operating point will move to B. During this range of load variation, there is only one point at which the PV module provides its maximum power point (MPP). This occurs when load resistance is equal to the optimal value (load resistance at MPP: RL = Ropt). But it’s very difficult to select a fixed load which matches this value, and even if it is done, this point itself changes under changed climatic conditions.
To overcome this problem, a maximum power point tracker system (MPPT) must be used to force the PV module’s operating point at the MPP. MPPT can extract more than 97% of the PV power when properly optimized. The goal of the MPPT is to match the impedance of load to the optimal impedance of PV module [1]. MPPT uses the DC-DC converter for a different purpose: regulating the input voltage at the PV module’s MPP and providing load matching for the maximum power transfer [2].
On the other hand, when a DC-DC converter is interposed between the PV module and the load, the operating point depends on the impedance seen by the module (Rin), which shows dependence on two parameters: RL and duty cycle (α). Thus, under different loads, the duty cycle can be adjusted to change Rin to match Ropt at any cli-

Figure 1. Operating point of a PV module with different resistive load.
matic condition. Several methods are proposed for MPPT algorithm: system oscillation [1], look-up table [3], fractional open-circuit voltage [4], fractional short-circuit current [5,6], current sweep [7], perturbation and observe (P&O) [8], Hill Climbing [9-11], conductance incremental [12-14], a biological swarm chasing algorithm [15], Ripple correlation control [16], fuzzy logic control [17,18] and neural network [19]. However, the parameters’ sizing of the different topologies of DC-DC converters has not been studied widely although this sizing affects significantly the optimum operation of the PV systems. For example, the bad choice of the converter according to the load makes the MPPT less useful and this affects the converter efficiency. Also, the bad converter sizing affects significantly its efficiency.
In this paper, we propose an analyzing method of design optimization of inductance and capacitance of three basic topologies of DC-DC converters connected to a PV module and controlled by MPPT when climatic conditions (cell temperature and solar irradiance) change throughout a day for a suitable load resistor using MATLAB simulation. The objective of this work is to achieve optimal efficiency for each converter.
2. Theory Development
2.1. PV Module Modelling
A single exponential model [20-22] (one diode model) considered as the most popular model for solar cells describes the relationship between voltage and current. This relationship given by a PV module is written as:
 (1)
(1)
where Ns is the number of cells connected in series. This model contains five parameters, photogenerated current (Iph), reverse saturation current (Is), series resistance (Rs,pv), shunt resistance (Rsh) and diode ideality factor (n). The one diode model circuit is shown in Figure 2.
To make a better model, the computation of Iph, Is and Rs,pv parameters includes temperature effects. The Rsh and n parameters are considered constant and equal respectively to 1000 Ω and 1.21. These two values are estimated to attain the best match with the I-V curves on the datasheet of the given PV module.
2.2. MPPT Method Analysis
The location of the MPP in the I-V curve of PV module is not known beforehand and always changes dynamically depending on irradiance and temperature. Therefore, the MPP needs to be located by tracking algorithm, which is the heart of MPPT controller. The goal of the MPPT is to match the load resistance RL to the optimal output resistance of PV module Ropt defined as:
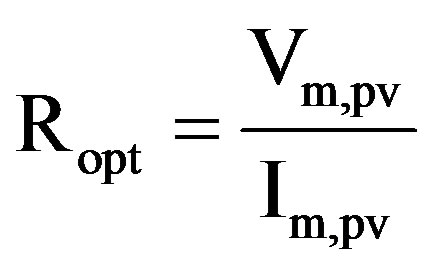 (2)
(2)
When RL matches with that of Ropt (Rin = Ropt), the maximum power transfer from PV to the load will occur.
The MPPT method used in this work is called: “output sensing method”, it measures the power change of PV at the output side of converter and uses the duty cycle as a control variable [2]. This control method employs the Perturbation and Observation (P&O) algorithm to locate the MPP. The flowchart of algorithm is shown in Figure 3.
In order to accommodate duty cycle as a control variable, the P&O algorithm [23] used here is a slightly modified version of the classic one, but the idea how it works is the same. The algorithm perturbs the duty cycle and measure the output power of converter. If the power is increased, the duty cycle is further perturbed in the same direction; otherwise the direction will be reversed. When the output power of the converter is reached at the
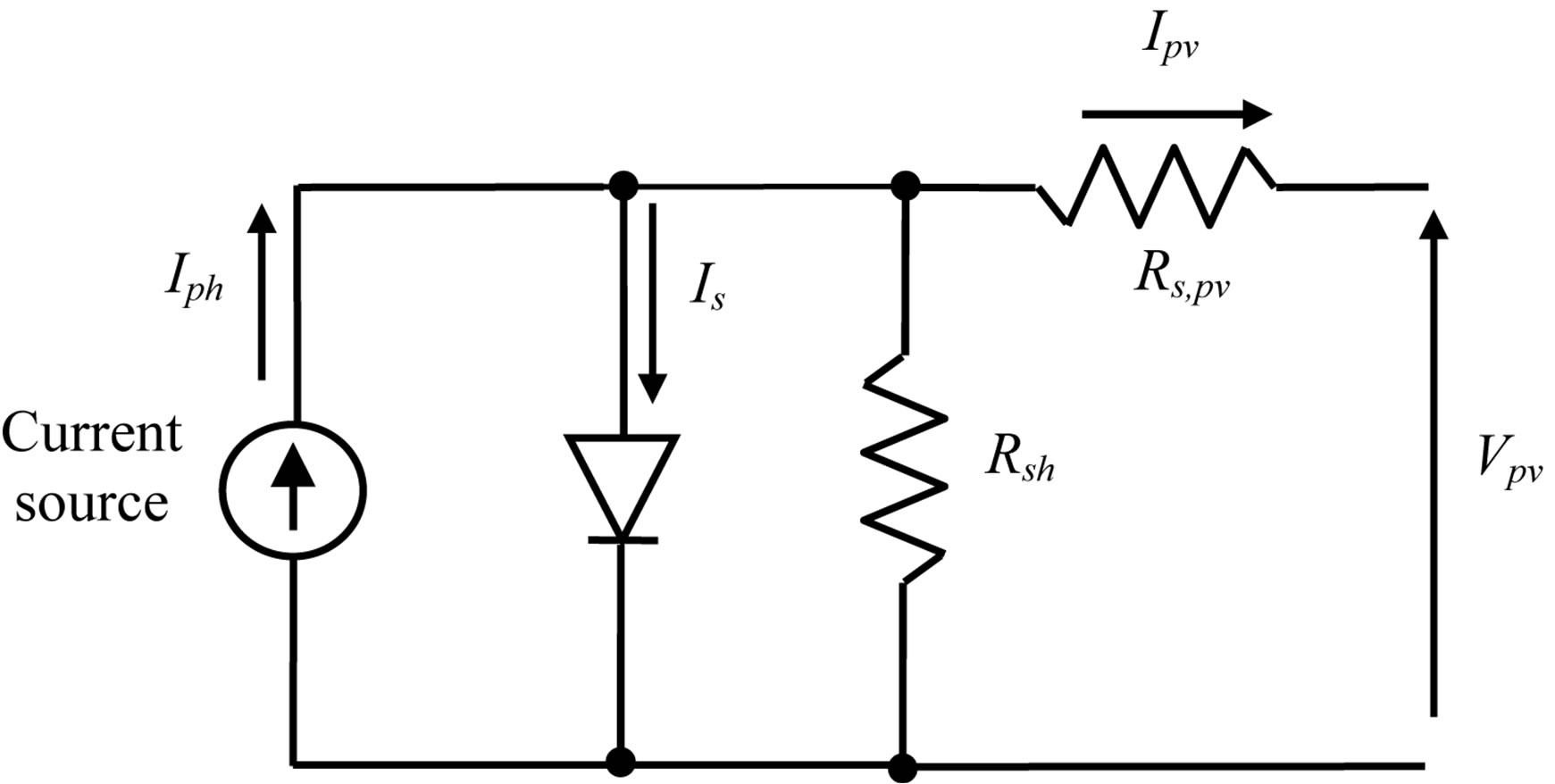
Figure 2. A one diode equivalent circuit for PV module used in the MATLAB simulation.
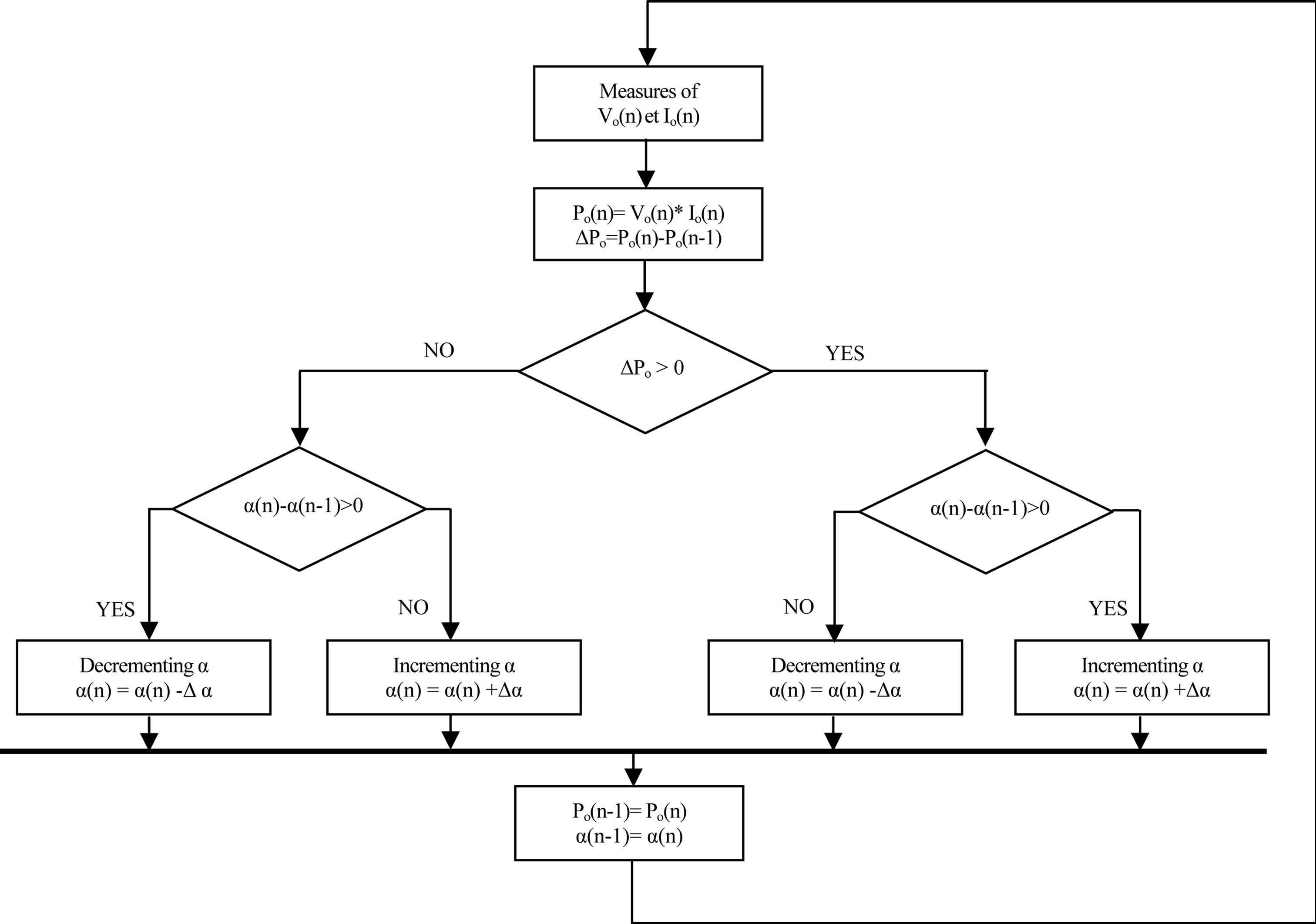
Figure 3. Flowshart of P&O algorithm with the output sensing method.
peak, the PV module is supposed to be operating at MPP.
2.3. Operation of DC-DC Converters
The three basic DC-DC converters commonly used in PV systems are: buck, boost and buck-boost converters [24], are shown in Figure 4. The characteristic parameters of each topology can be described by the following parameters listed in Table 1 [25].
The converter can operate in two distinct modes of operation, the continuous conduction operation (CCO) or the discontinuous conduction operation (DCO). The CCO occurs when inductance current is always greater than zero and is preferred for high efficiency and good utilization of semiconductors switches and passive components [26]. The DCO is not preferred since the dynamic order of the converter is reduced [26].
The inductance L is used to filter the input and output current of the converter. Lbo is the boundary value of L for a given duty cycle α to ensure that the chopper is operated in CCO mode [25]. The capacitance C allows minimizing the output voltage ripple of the converter, so Cbo is the boundary capacitance value required for a given duty cycle α to reduce the output ripple voltage of the converter to specified desired value [25]. The above parameters can be computed using the relationships given in Table 1.
We note that these relations were deduced under the assumption that the converter is lossless and always operates in CCO mode.
3. Results and Discussions
The following simulation work is carried out under the climatic conditions in Tunisia. The SIEMENS SM-50H [27] was selected as photovoltaic generator for the simulation. The module consists of 33 single-crystalline silicon solar cells connected in series and provides 50 W as nominal maximum power in STC. The characteristic parameters of this module are shown in appendix.
Figure 5 shows the climatic data used for this study. The set of these data is the measurements of a sunny day of March in Tunisia. The figure shows that the lowest irradiance is 191 W/m2 at 26.7˚C while the highest irradiance was 1064 W/m2 at 40˚C. From these data, we calculate values of optimum resistance Ropt at highest

Figure 4. DC-DC converters diagram commonly used. (a) Boost; (b) Buck; (c) Buck-boost.

Table 1. Characteristic parameters for each DC-DC converter [25].
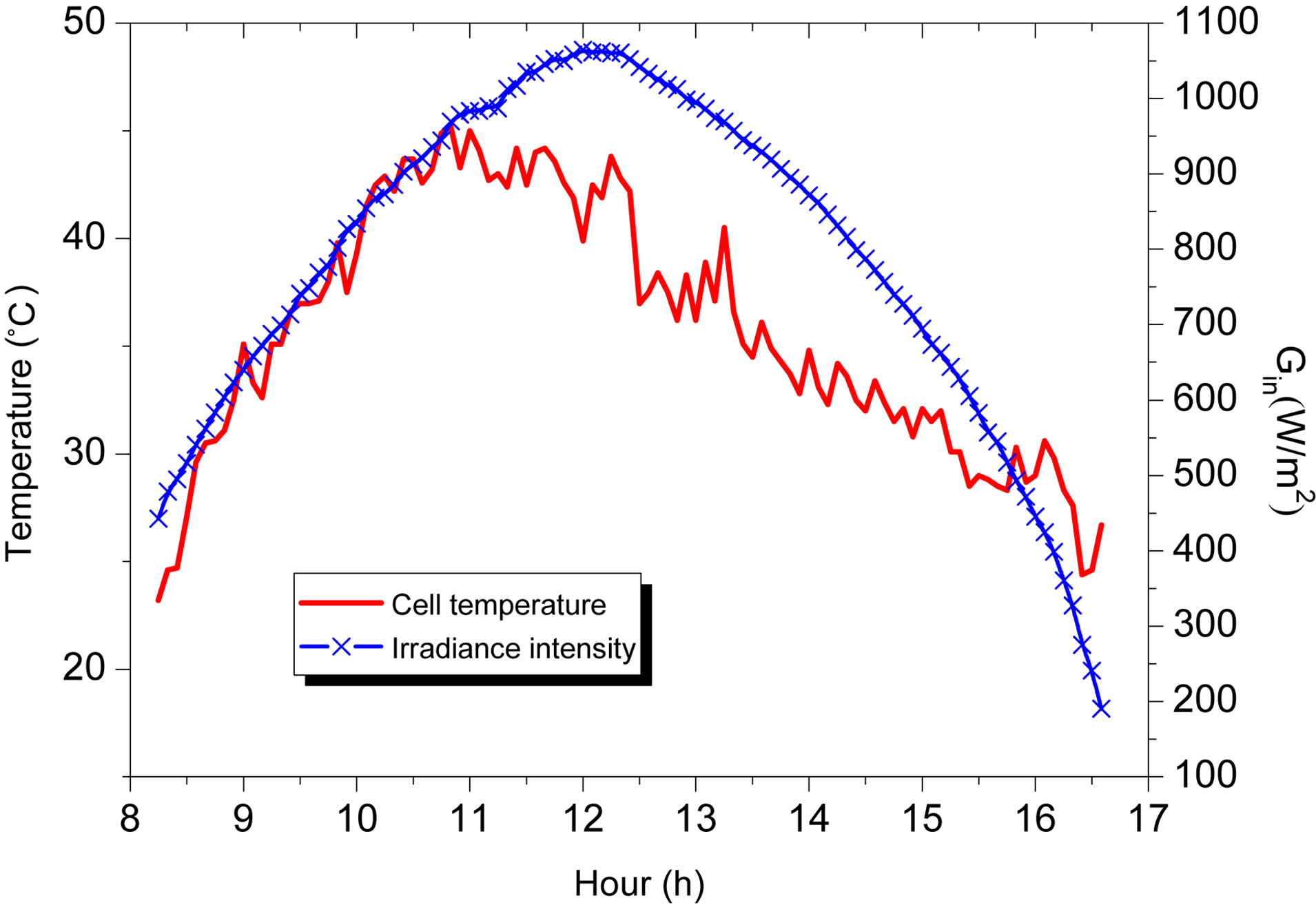
Figure 5. Irradiance and cell temperature data for a sunny day of March in Tunisia.
climatic conditions (Ropt,(min)) shown in the middle of the day (12 h) and Ropt at lowest climatic conditions (Ropt,(max)) shown at the end of the day. Thus, Figure 6 demonstrates the variation of Ropt throughout the day. Table 2 summarizes these data.
The irradiance and temperature parameters change systemically during the day, consequently the MPP will change; thus, the duty cycle must be adjusted in order to track the new MPP. Hence, boundary values of capacitance and inductance (Cbo, Lbo) will also change (Table 1). The values of these components sized for a certain duty cycle may be less than the chosen converter design parameters. Therefore, the converter may work in DCO mode with large output voltage ripple which reduces the converter efficiency.
In order to reach the ideal choice of these parameters, we will study the behaviour of Cbo and Lbo later along the day according to changing in climatic conditions using the following criteria:
• a typical switching frequency for all DC-DC converters of 50 KHz.
• suitable load resistor associated to each converter.
• a maximum percentage ripple of output voltage 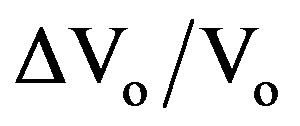 equal to 2%.
equal to 2%.
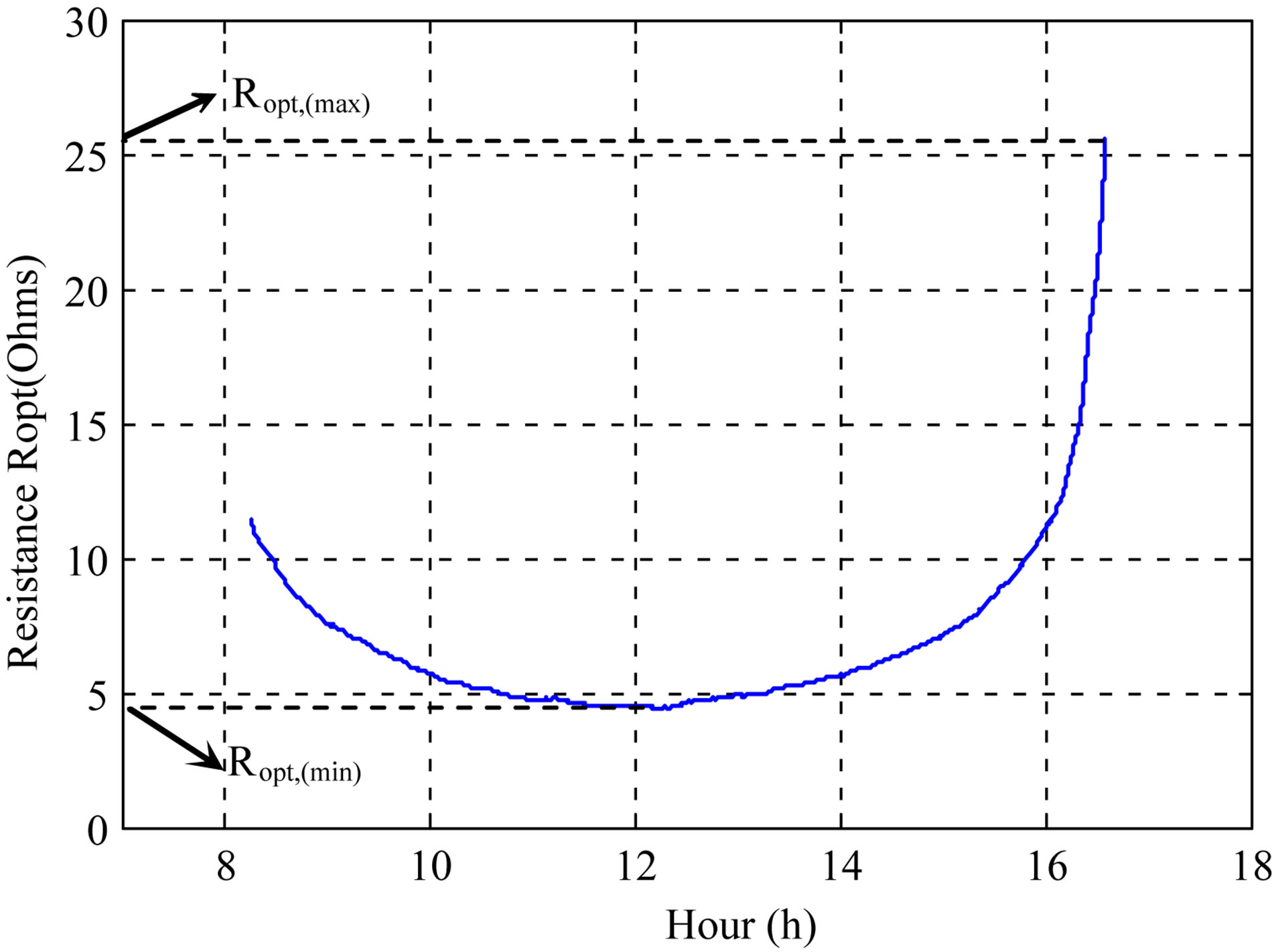
Figure 6. Optimum resistance trajectory for a sunny day of March in Tunisia.

Table 2. Module characteristic in low and high climatic conditions.
3.1. Design for Buck Converter
For buck converter, the resistor load is chosen to be RL = 3 Ω < Ropt,(min) as presented in Figure 7(a). The effect of duty cycle α on Lbo and Cbo is demonstrated in Figure 7(b), where Cbo is drawn with different values of filter inductance L. We note that curve 1 corresponds to L = Lbo,(max), and then other curves are obtained by increasing L in steps of 2 µH. In curve 2, when L = Lbo, it’s apparent that Cbo is constant and independent of α, but increasing L over Lbo,(max) gives a significant decreasing in Cbo. The impedance matching is available at A to B which corresponds to a variation of duty cycle between 0.347 and 0.825 (Figure 7(a)) and this leads to a decreasing of Lbo from 19.58 µH (Lbo,(max)) to 5.25 µH (Lbo,(min)). At point C, the duty cycle is α = 0.6, and Lbo = L1,bo = 12 µH. If climatic conditions changes, this point moves to D corresponding to α = 0.5 and Lbo will take a value of Lbo = L2,bo = 15 µH > L1,bo. It turns out that the choice of L1,min will operate the buck converter in DCO mode. Therefore, L must be chosen larger than Lbo,(max), which occurs at the lowest climatic conditions for loads lower than Ropt,(max) to give a CCO mode regardless of the climatic conditions. Some designers select a value 25 percent larger than Lbo,(max) to ensure that inductor current is continuous [25].
In curve 1, it can be seen that Cbo decrease from 83.3 µF (Cbo,(max)) to 22.3 µF (Cbo,(min)) when the operating point varies from A to B. For a given climatic condition,

Figure 7. Effect of duty cycle on (L,C) design of buck converter.
if the duty cycle is α = 0.6 corresponding to point C, Cbo = C1,bo = 51 µF. If this point moves to D corresponding to α = 0.5, Cbo will increase to C2,bo = 63.8 µF > C1,bo. Consequently, the choice of C1,bo will make the output voltage ripple of the buck converter larger than the desired limit value. In order to avoid this problem, the filter capacitance C must be designed for a value larger than Cbo,(max), which is obtained at the lowest climatic conditions for loads lower than Ropt,(max).
3.2. Design for Boost Converter
In this study, the resistor load is chosen to be RL = 30 Ω > Ropt,(max) as shown in Figure 8(a). Figure 8(b) shows the variation of Lbo and Cbo according to α. It can be seen that when α is increased, Cbo will increase linearly. When the climatic conditions changes from the lowest to the highest value, the operating point moves from A to B respectively. Thereafter, the impedance matching is available at A to B by varying duty cycle between 0,14 and 0.617 (Figure 8(a)) which leads to an increase of Cmin from 4.66 µF (Cbo,(min)) to 20.58 µF (Cbo,(max)). Therefore, the filter capacitance C must be greater than Cmin,(max) which occurs at the highest climatic conditions for loads greater than Ropt,(min). Lbo takes a hill curve form, the peak of the hill is noted Lbo,(peak) = 44.77 µH obtained for a duty cycle αm = 1/3. This particular value of duty cycle is obtained while solving the following equation

Figure 8. Effect of duty cycle on (L,C) design of boost converter.
for the chosen load value and the switching frequency given by:
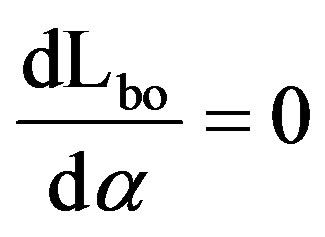 , where
, where 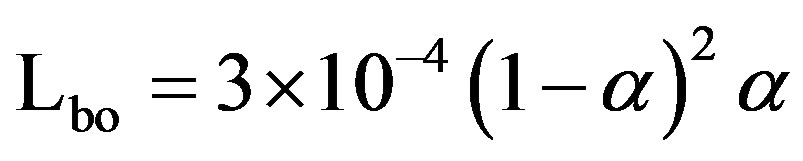 (3)
(3)
We note that Lbo,(peak) always occurs at αm = 1/3 only if it is included in the operating range of duty cycle variation and this value is constant and independent of any other parameters. Finally, Lbo,(peak) = Lbo,(max) in this study.
3.3. Design for Buck-Boost Converter
Several previous studies investigated that the buck-boost converter has not any constraint for the choice of load. In our study, Ropt,(min) < RL = 8 Ω < Ropt,(max), is chosen as shown in Figure 9(a). When the operating point moves from A to B by changing in climatic conditions from the lowest to the highest, the impedance matching is available at A to B by varying duty cycle between 0.36 to 0.575. And subsequently, a linear increase of Cbo from 45 µF (Cbo,(min)) to 71.8 µF (Cbo,(max)) is shown in Figure 9(b). Whereas, Lbo is decreased linearly from 32.77 µH (Lbo,(max)) to 14.45 µH (Lbo,(min)). To ensure that the buck-boost converter operates in CCO mode, the inductance L must be chosen larger than Lbo,(max), which is always at the lowest climatic conditions for any loads values. And, to ensure a limit value of the ripple in output voltage at a desired value, C must be designed for a value larger than Cbo,(max), which is always at the highest cli-

Figure 9. Effect of duty cycle on (L,C) design of buck-boost converter.
matic conditions for any loads values.
4. Conclusions
The goal of this study is to achieve the highest performance of three topologies of DC-DC converters connected to a single PV module and controlled by MPPT throughout a clear day in Tunisia. These topologies of converters are commonly used in PV systems.
This goal can be achieved only if each converter is properly sized. Thereafter, the effect of changing climatic conditions on the choice of filter inductance and capacitance of each type of converter is investigated. We stated that the inductance for these converters must be greater than Lbo,(max) to guarantee a CCO mode. We have investigated that this value occurs at the lowest climatic conditions for all DC-DC converters except the boost converter which may occur at any location during the period of system operating. Also in order to limit the output voltage ripple of DC-DC converters below a required value, we stated that the capacitance must be larger than Cbo,(max). We have investigated that this value occurs at the lowest conditions for buck converter and at the highest conditions for boost and buck-boost converters.
REFERENCES
- H. S. H. Chung, K. K. Tse, S. Y. Ron Hui, C. M. Mok and M. T. Ho, “A Novel Maximum Power Point Tracking Technique for Solar Panels Using a SEPIC or Cuk Converter,” IEEE Transactions on Power Electronics, Vol. 18, No. 3, 2003, pp. 717-724. http://dx.doi.org/10.1109/TPEL.2003.810841
- A. Oi, “Design and Simulation of Photovoltaic Water Pumping System,” Master of Science in Electrical Engineering Thesis, California Polytechnic State University, San Luis Obispo, 2005.
- H. Tarik Duru, “A Maximum Power Tracking Algorithm Based on Impp = f(Pmax) Function for Matching Passive and Active Loads to a Photovoltaic Generator,” Solar Energy, Vol. 80, No. 7, 2006, pp. 812-822. http://dx.doi.org/10.1016/j.solener.2005.05.016
- H. J. Noh, D. Y. Lee and D. S. Hyun, “An Improved MPPT Converter with Current Compensation Method for Small Scaled PV-Applications,” Proceedings of the 28th Annual Conference on Industrial Electronics Society, Sevilla, 5-8 November 2002, pp. 1113-1118.
- T. Esram and P. L. Chapman, “Comparison of Photovoltaic Array Maximum Power Point Tracking Techniques,” IEEE Transactions on Energy Conversion, Vol. 22, No. 2, 2007, pp. 439-449. http://dx.doi.org/10.1109/TEC.2006.874230
- S. Yuvarajan and S. Xu, “Photo-Voltaic Power Converter with a Simple Maximum-Power-Point-Tracker,” Proceedings of the 2003 International Symposium on Circuits and Systems ISCAS’03, Vol. 3, 2003, pp. III-399-III-402.
- M. Bodur and M. Ermis, “Maximum Power Point Tracking for Low Power Photovoltaic Solar Panels,” Proceedings of the 7th Mediterranean Electrotechnical Conference, New York, 12-14 April 1994, pp. 758-761.
- F. Liu, Y. Kang, Y. Zhang and S. Duan, “Comparison of P&O and Hill Climbing MPPT Methods for Grid-Connected PV Converter,” Proceedings of the 3rd IEEE Industrial Electronics and Applications Conference ICIEA, Singapore City, 3-5 June 2008, pp. 804-807.
- W. Xiao and W. G. Dunford, “A Modified Adaptive Hill Climbing MPPT Method for Photovoltaic Power Systems,” Proceedings of the 35th Annual IEEE Power Electronics Specialists Conference PESC’04, Aachen, 20-25 June 2004, pp. 1957-1963.
- H. Al-Atrash, I. Batarseh and K. Rustom, “Statistical Modeling of DSP-Based Hill-Climbing MPPT Algorithms in Noisy Environments,” Proceedings of the 31st Annual IEEE Applied Power Electronics Conference and Exposition APEC 2005, Vol. 3, No. 6-10, 2005, pp. 1773- 1777.
- E. Koutroulis, K. Kalaitzakis and N. C. Voulgaris, “Development of a Microcontroller-Based, Photovoltaic Maximum Power Point Tracking Control System,” IEEE Transactions on Power Electronics, Vol. 16, No. 21, 2001, pp. 46-54. http://dx.doi.org/10.1109/63.903988
- J. Sachin and V. Agarwal, “An Integrated Hybrid Power Supply for Distributed Generation Applications Fed by Nonconventional Energy Sources,” IEEE Transactions on Energy Conversion, Vol. 23, No. 2, 2008, pp. 622-631. http://dx.doi.org/10.1109/TEC.2008.918631
- N. Femia, D. Granozio, G. Petrone, G. Spaguuolo and M. Vitelli, “Optimized One-Cycle Control in Photovoltaic Grid Connected Applications,” IEEE Transactions on Aerospace and Electronic Systems, Vol. 42, No. 3, 2006, pp. 954-972. http://dx.doi.org/10.1109/TAES.2006.248205
- J. H. Lee, H. S. Bae and B. H. Cho, “Advanced Incremental Conductance MPPT Algorithm with a Variable Step Size,” Proceedings of the 12th International Power Electronics and Motion Control Conference EPE-PEMC, Portoroz, 30 August-1 September 2006, pp. 603-607.
- L. Chen, C. Tsai, Y. Lin and Y. Lai, “A Biological Swarm Chasing Algorithm for Tracking the PV Maximum Power Point,” IEEE Transactions on Energy Conversion, Vol. 25, No. 2, 2010, pp. 484-493. http://dx.doi.org/10.1109/TEC.2009.2038067
- D. Casadei, G. Grandi and C. Rossi, “Single-Phase Single-Stage Photovoltaic Generation System Based on a Ripple Correlation Control Maximum Power Point Tracking,” IEEE Transactions on Energy Conversion, Vol. 21, No. 2, 2006, pp. 562-568. http://dx.doi.org/10.1109/TEC.2005.853784
- T. L. Kottas, Y. S. Boutalis and A. D. Karlis, “New Maximum Power Point Tracker for PV Arrays Using Fuzzy Controller in Close Cooperation with Fuzzy Cognitive Network,” IEEE Transactions on Energy Conversion, Vol. 21, No. 3, 2006, pp. 793-803. http://dx.doi.org/10.1109/TEC.2006.875430
- N. Khaehintung, K. Pramotung, B. Tuvirat and P. Sirisuk, “RISC Microcontroller Built-In Fuzzy Logic Controller of Maximum Power Point Tracking for Solar-Powered Light-Flasher Applications,” Proceedings of the 30th Annual Conference of the IEEE Industrial Electronics Society, Busen, 2-6 November 2004, pp. 2673-2678.
- L. Zhang, Y. Bai and A. Al-Amoudi, “GA-RBF Neural Network Based Maximum Power Point Tracking for Grid-Connected Photovoltaic Systems,” Proceedings of the International Conference on Power Electronics Machines and Drives, Bath, 4-7 June 2002, pp. 18-23. http://dx.doi.org/10.1049/cp:20020083
- R. Chenni, M. Maklouf, T. Kerbache and A. Bouzid, “A Detailed Modeling Method for Photovoltaic Cells,” Energy, Vol. 32, No. 9, 2007, pp. 1724-1730. http://dx.doi.org/10.1016/j.energy.2006.12.006
- M. Chegaar, G. Azzouzi and P. Mialhe, “Simple Parameter Extraction Method for Illuminated Solar Cells,” SolidState Electronics, Vol. 50, No. 7-8, 2006, pp. 1234-1237. http://dx.doi.org/10.1016/j.sse.2006.05.020
- M. A. De Blas, J. L. Torres, E. Prieto and A. Gacía, “Selecting a Suitable Model for Characterizing Photovoltaic Devices,” Renewable Energy, Vol. 25, No. 3, 2002, pp. 371-380.
- C. Cabal, “Optimisation Énergétique de l’Étage d’Adaptation Électronique Dédié à la Conversion Photovoltaique,” Ph.D. Thesis, CNRS, University of Toulouse III, Toulouse, 2008.
- J. M. Enrique, E. Durán, M. Sidrach-de-Cardona and J. M. Andújar, “Theoretical Assessment of the Maximum Power Point Tracking Efficiency of Photovoltaic Facilities with Different Converter Topologies,” Solar Energy, Vol. 81, No. 1, 2007, pp. 31-38. http://dx.doi.org/10.1016/j.solener.2006.06.006
- D. W. Hart, “Power Electronics,” McGraw-Hill Companies Inc., New York, 2010.
- M. H. Rashid, “Power Electronics Handbook,” 2nd Edition, Academic Press, New York, 2007.
- SIEMENS, “Solar Module SM50-H 50W,” MonoCrystalline Photovoltaic Module Datasheet. http://www.a1solar.co.uk/sm50-h.pdf
Nomenclature
Vpv: output voltage from PV module (V).
Ipv: output current from PV module (A).
Av: converter voltage gain.
Ai: converter current gain.
Rin: input resistance to converter (Ω).
ΔVo: output ripple voltage of converter (V).
Lbo: boundary value of inductance (µH).
Cbo: boundary value of capacitance (µF).
RL: load resistance (Ω).
Ropt: PV output resistance at MPP (Ω).
Is: reverse saturation current.
Pm,pv: PV module maximum power (W).
Vm,pv: PV voltage at MPP (V).
Im,pv: PV current at MPP (A).
Gin: incident irradiance intensity (W/m2).
VT: thermal voltage (VT = (K·T)/q)
K: Boltzmann’s constant (J/K).
T: cell temperature (˚C).
q: electron charge (1.602 × 10−19 C).
Vo: output voltage from converter (V).
Io: output current from converter (A).
Po: output power from converter (W).
Ns: number of series-connected cells.
α: converter duty cycle.
Rs,pv: PV module series resistance (Ω).
Rsh: shunt resistance (Ω).
n: diode ideality factor.
Iph: total photogenerated current (A).
f: switching frequency of DC-DC converter (KHz).
Abbreviations
STC: Standard Test Condition.
MPP: Maximum Power Point.
MPPT: Maximum Power Point Tracker.
CCO: Continuous Condition Operation.
DCO: Discontinuous Condition Operation.
NOTES
*Corresponding author.

