Journal of Materials Science and Chemical Engineering
Vol.05 No.12(2017), Article ID:81292,12 pages
10.4236/msce.2017.512004
Determination of Volume Conductivity of Polyethylene Using Positive Corona, When the Current through the Sample Depends Linearly on Grid Potential
Pranvera Dhima1,2, Floran Vila1
1Department of Physics, University of Tirana, Tirana, Albania
2Laboratory of Institute of Communication Technology, University of Technology, Darmstadt, Germany
Copyright © 2017 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: November 16, 2017; Accepted: December 22, 2017; Published: December 25, 2017
ABSTRACT
In this paper we determine for the first time the volume conductivity of polyethylene (of 40 μm and 50 μm thickness), using the positive corona triode. A general theory of flowing of the current through the sample, when it depends linearly on the grid potential, is formulated. A concrete methodology for the definition of volume conductivity is composed. The volume conductivity of polyethylene lies within the interval: . These results obtained using the corona triode are closely similar to those obtained using the standardized “static” methods, thus showing its superiority to the “dynamic” method of electronic radiation.
Keywords:
Polyethylene, Positive Corona Triode, Volume Conductivity

1. Introduction
The electrical properties of polymers are of great importance for various applications. Polyethylene is the most extensively used thermoplastic polymer, due to its excellent electrical, thermal, and mechanical properties.
Conductivity, an important parameter of polymer characteristics, is traditionally performed with the classic “static” method (a system of electrodes) [1] . But, in addition, a “dynamic” method, based on electron-beam irradiation of thin samples of polyethylene (PE) is used for the measurement of the conductivity [2] [3] [4] .
In this paper we determine for the first time the volume conductivity of polyethylene using the positive corona triode: corona point, grid, grounded electrode.
For this purpose, firstly, a general theory of flowing of the current through the sample, when it depends linearly on the grid potential, is formulated. And then, after receiving the experimental data, a concrete methodology for the definition of volume conductivity is composed.
The results obtained by the proposed formula, are closely similar to those obtained using standardized “static” methods, thus showing a superiority of the corona triode method as compared to the “dynamic” method of electron-beam irradiation.
2. Theoretical Considerations
Sample Current
The current through the polymer samples is realized by the corona discharge in the point to plane geometry, described in detail in [5] .
While a high positive voltage is applied on the corona electrode the air becomes ionized, creating positive ions and free electrons near the corona, in plasma region (Figure 1). In the unipolar drift region only positive ions exist. The unipolar ions are propelled towards the sample surface and could enter the surface layer of the material, even into its inside [6] .
Figure 1. Model of a positive corona discharge (The sample thickness is exaggerated in this figure).
The positive ions that arrive at the surface of the sample, transfer their charge to it, introducing potential gradients on the surface and in the bulk of the sample. Thus, a part of the charges are transported along the surface and the other part are transported through the bulk, producing an electric field in the bulk of the sample [7] [8] .
The time variation of the first part of charges determines a displacement current and the time variation of the other part of charges determines a conduction current that depends on the kind of process that occurs in the material [5] [8] . Thus, assuming that the system is a capacitor, the total current intensity , at a moment of time t, will be:
(1)
where, , , and , are volume conductivity, the surface and dielectric constant of the square sample with a length side , respectively. is the average electric field strength, caused by the potential difference between the surface of the sample with thickness and the grounded electrode [9] .
To simplify the analysis, it was assumed that surface trap states are uniformly distributed, in a thin layer [10] . Consequently, the surface density of charges embedded, and the potential that they cause will be considered uniform [5] [11] [12] .
Thus, we can write:
(2)
Taking into consideration the Equation (2) as well as fact that , the Equation (1) will be presented as:
(3)
The volume conductivity, in the differential Equation (3) is the unknown quantity that we intend to determine. Meanwhile, the other quantities ( , , , ) are known, or are experimentally determined [ and ]. But, to solve that equation, the relationship between the interdependent quantities and , should be known in advance. This raise the question: what is the relationship between and , two quantities that can be measured?
The charge density is closely related to the current across the sample and the surface potential measured. Thus, the charge condition inside the material can be represented according to the surface potential measured [13] . The facts indicate that this relationship can be different in various situations [14] [15] [16] . Thus, let us turn to the experiment to find it out.
3. Experimental Method
3.1. Experimental Setup
The used schematic diagram of corona triode is shown in Figure 2(a) and Figure 2(b).
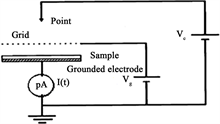

Figure 2. Schematic diagram of corona triode (a); corona triode (b).
PE square samples of 2.5 cm side length of 40 μm and 50 μm thickness were used in this work. One face of the samples was coated by an aluminum foil, using a copper double-sided sticky layer. This ensures a good contact with the grounded electrode (circular of 20 mm diameter and 8 mm high) on which the samples were laid.
The other free surface has been exposed for 30 s to a corona discharge generated by a corona electrode (point, 1 mm diameter) situated above the grounded electrode and connected to a DC high-voltage supply (FUG HCN 14-12500). Positive 10.09 kV voltage was applied to the corona electrode. A metallic grid connected at different DC potential (Model 240 A, Keithley Instruments) of the same polarity as that of the corona electrode was inserted between the point and the sample surface. Thus, a better control over the potential to which the surface was charged, and over the charge uniformity could be achieved [5] [11] [12] . Distance between the grid and the grounded electrode was 10 mm; the distance from the grid to the corona electrode was 7 mm. A digital picoampere meter (Model 445, Keithley Instruments) was used for measuring the sample charging current. As soon as the high-voltage supply of the corona charger was turned-off (within 3 seconds), the sample was moved to an electrostatic voltmeter (Model 244, equipped with a probe model 1017) for surface potential measurement, without physical contact. We used new samples for each measurement.
3.2. Experimental Results
The experiments with corona triode, give us the opportunity to study the corona discharge influence in electrostatic charging process of PE. The determination of the charging current vs. grid potential curves show important results related to electrical characteristics [5] .
We found out the relationship between the current flowing through the sample and its surface potential, via the grid potential. Therefore, two dependencies were determined simultaneously, the current flowing through the sample and its surface potential, as a function of the grid potential. The experimental graphs of both of the above dependencies, of PE (40 μm and 50 μm thickness), are shown in Figure 3 and Figure 4, respectively.
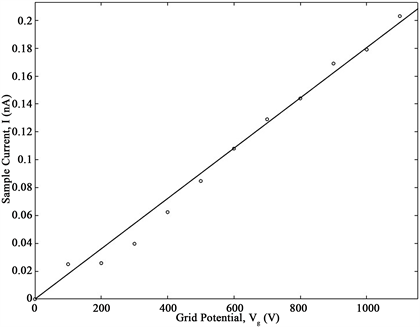

Figure 3. Dependence of the current flowing through the (a) 40 μm thickness PE sample and (b) 50 μm thickness PE sample, on the grid potential (Solid lines represent linear fittings for each case, with adjusted R2 values of 0.9872 and 0.9770, respectively).
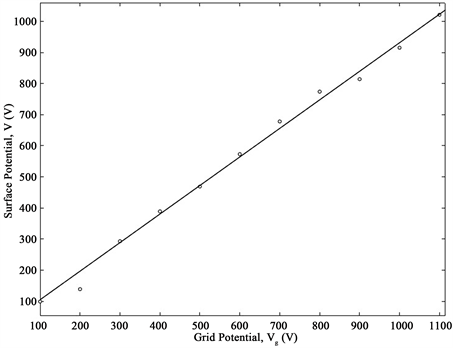
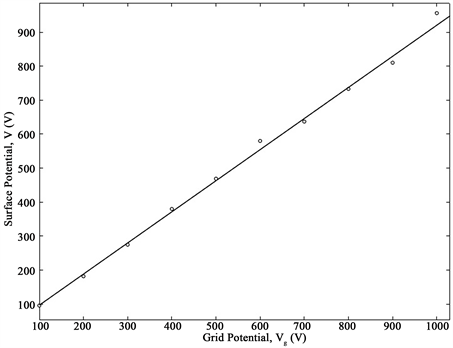
Figure 4. Dependence of the surface potential on the grid potential, of (a) 40 μm thickness PE sample and (b) 50 μm thickness PE sample (Solid lines represent linear fittings for each case, with adjusted R2 values of 0.9939 and 0.9956, respectively).
The experimental results, shown in Figure 3 present this type of dependency:
(4)
meanwhile, those shown in Figure 4 present a type of dependency like:
(5)
Thus, considering the Equation (4) and the Equation (5), the required relationship between the current flowing through the sample and its surface potential is obtained and is of the type:
(6)
where:
(7)
4. Determination of Volume Conductivity
4.1. Analysis of the Case of Linear Dependence of the Current Flowing through the Sample on the Grid Potential,
Let us turn to the determination of volume conductivity , that is the fundamental objective of this study. The definition of the relationship between the sample current and the surface potential in Equation (6), allows us to write the Equation (3) in the following form:
(8)
where,
and (9)
The solution of the Equation (8) is associated with logarithmic and exponential expressions. If the below conditions for the presentation of the logarithmic and series expansion of exponential functions:
and (10)
are satisfied, then the solution has the form:
(11)
where t is the time interval in which the current flows through the sample, whereas [9] .
In the Equation (11), is the only unknown quantity that contains , the object of our determination. Related with , Equation (11) represents an equation of the second degree. The only solution that can be accepted, under our experimental conditions, is:
(12)
as it satisfies the condition given by the Equation (10) [9] . Thus, according to the Equation (9) as well, we determine:
(13)
Let us note:
(14)
that is a constant for a given sample, as and are the thickness and the length side of square sample, respectively.
Thus, using the constants , , [see Equation (7)] and the quantity , the Equation (13) can be written:
(15)
4.2. Discussion
Firstly, let us discuss about the important experimental constant k. in view of Equation (7), Equation (9) and Equation (17), the constant can be written:
(16)
Thus, according to Equation (10), we can write:
(17)
where,
(18)
But, to permit the constant tobeused in all the allowed zone of experimental measurements, itneedstobedetermined in the case when has the lowest value.
The experiments show that , thus we may obtain:
(19)
In view of Equation (17) and Equation (19) we can conclude:
(20)
Secondly, let us just clarify what is the conductivity zone, determined by the Equation (15).
Let us express from Equation (15), in its final form, as a function of and . We have:
(21)
Whereas, according to Equation (9) and Equation (10): or using the constants and , we obtain:
(22)
The above relation gives them a the matical interval of , valid for . But, from the theory formulated by us, in view of Equation (5) and Equation (19), derives or, if we note we have:
(23)
Thereof derives that, in our argumentations, only the surface potential values that satisfy the condition:
(24)
are accepted. Thus, according to Equation (21) and Equation (23) as well, the interval that should be conditioned by extremum values of , is determined as below:
(25)
where:
and (26)
Definitely, in the theory developed by us, only those experimental facts which are subject to Equation (20), Equation (23) and Equation (24) are accepted. While is defined by the Equation (21) and lies in the interval determined by Equation (25).
4.3. Numerical Calculation
Let us present, in the Table 1, the calculations based on experimental results for PE of 40 μm and 50 μm thickness, respectively.
It can be seen that the experimental constants in both cases, satisfy the condition given by Equation (20). While the acceptable coefficients, in accordance with the Equation (23), satisfy the conditions: and , respectively. Thereof derives that, [see Equation (24)], the surface potential values higher than 1020 V cannot be accepted. So, in accordance also with Equation
Table 1. The calculations based on experimental results for PE of 40 μm and 50 μm thickness.
(25), volume conductivities, in both samples, lie within the intervals: and , respectively.
A review of the literature, regarding the electrical properties of PE [3] [11] [17] [18] [19] [20] , shows that its conductivity lies within the range to , in full accordance with our experimental measurement results. On the other hand, as it can be seen, both intervals overlap each other. Thus, definitely, it can be said that conductivity of PE lies within the interval: .
Let us compare the above results, obtained with the corona triode, with those obtained before, using standardized “static” methods (a system of electrodes) and “dynamic” methods (electronic irradiation of PE) [3] .
The studies show [3] [11] [19] [20] , that using the “static” methods, the obtained average volume conductivity value of PE is , very close to the above interval of determination.
While, using the “dynamic” methods [2] [3] , the obtained value for PE irradiated with electron beam is .
It can be clearly seen that the corona triode method is superior to the “dynamic” method because its results are closely similar to those obtained using the standardized “static” methods. We emphasize that the differences, generally, are not related with the order of magnitude but only with its coefficient. As there are differences between the above mentioned methods, these differences in results are to be expected. In the first case, the positive ions of corona triode are used. In the second case, electron “bombardment” from a scanning electron microscope is used, thus the volume resistivity is dependent on electrons energy and on the irradiation time as well. While in the third case, a three electrode differently standardized system is used [3] .
5. Conclusions
In this paper we determine for the first time the volume conductivity of polyethylene, using the positive corona triode: corona point, grid and grounded electrode. The formulated theory and the proposed methodology, when the current flowing through the sample is proportional to its surface potential, allows the precise determination of the interval.
The volume conductivity ( ) interval for PE is defined as the overlap of the two intervals for PE of 40 μm and 50 μm thickness.
The obtained results, using the corona triode are closely similar to those obtained using the standardized “static” methods, thus showing its superiority to the “dynamic” method of electronic radiation.
Cite this paper
Dhima, P. and Vila, F. (2017) Determination of Volume Conductivity of Polyethylene Using Positive Corona, When the Current through the Sample Depends Linearly on Grid Potential. Journal of Materials Science and Chemical Engineering, 5, 40-51. https://doi.org/10.4236/msce.2017.512004
References
- 1. (1993) Standard Test Methods for DC Resistance or Conductance of Insulating Materials, ASTM Designation D 257-93, 103-119.
- 2. Vila, F., Sessler, G. M. (2001) Influence of Electron Beam Irradiation on Electric Parameters of Dielectric Materials. Journal of Electrostatics, 51 & 52, 146-152.https://doi.org/10.1016/S0304-3886(01)00092-4
- 3. Vila, F., Sessler, G. M. and Sykja, H. (2005) The Influence of Electron Beam Irradiation on the Volume Resistivity of Polyethylene and Kapton. Journal of Electrostatics, 63, 749-754. https://doi.org/10.1016/j.elstat.2005.03.039
- 4. Vila, F., Dhima, P. and Mandija, F. (2013) The Influence of Temperature on the Electrical Resistivity of the Cellular Polypropylene and Effect of Activation Energy. Springer Plus, 2, 472. https://doi.org/10.1186/2193-1801-2-472
- 5. Giacometti, A. and Oliveira, O.N. (1992) Corona Charging of Polymers. IEEE Transactions on Electrical Insulation, 27, 924-943. https://doi.org/10.1109/14.256470
- 6. Zhao, W.-B., Zhang, G.-J., Yang, Y. and Zhang Yan, Zh. (2007) Correlation between Trapping Parameters and Surface Insulation Strength of Solid Dielectric under Pulse Voltage in Vacuum. IEEE Transactions on Dielectrics and Electrical Insulation, 14, 170-178. https://doi.org/10.1109/TDEI.2007.302885
- 7. Batra, I.P., Kanazawa, K.K., Schechtman, B.H. and Seki, H. (1971) Charge-Carrier Dynamics Following Pulsed Photoinjection. Journal of Applied Physics, 42, 1124-1130. https://doi.org/10.1063/1.1660155
- 8. Giacometti, A., Fedosov, S. and Costa, M. (1999) Corona Charging of Polymers: Recent Advances on Constant Current Charging. Brazilian Journal of Physics, 29, 269-279. https://doi.org/10.1590/S0103-97331999000200009
- 9. Dhima, P. (2016) A Study about Polymer Electrisation. Scientific Report, Physics Department, Faculty of Natural Science, Tirana University, Tirana.
- 10. Li, J., Zhou, F., Min, D., Li, Sh. and Xia, R. (2015) The Energy Distribution of Trapped Charges in Polymers Based on Isothermal Surface Potential Decay Model. IEEE Transactions on Dielectrics and Electrical Insulation, 22, 1723-1732.https://doi.org/10.1109/TDEI.2015.7116370
- 11. Moreno, R.A. and Gross, B. (1976) Measurement of Potential Buildup and Decay, Surface Charge Density and Charging Currents of Corona-Charged Polymer Foil Electrets. Journal of Applied Physics, 47, 3397. https://doi.org/10.1063/1.323199
- 12. Hoang, A.T., Pallon, L., Liu, D., Serdyuk, Y.V., Gubanski, S.M. and Gedde, U.W. (2016) Charge Transport in LDPE Nanocomposites Part I-Experimental Approach. Polymers, 8, 87. https://doi.org/10.3390/polym8030087
- 13. Chen, G.-J., Xiao, H.-M. and Xia, Zh.-F. (2006) Charge Storage Characteristics in Hybrid Electret Film Consisting of Porous PTFE and PP with Negative Corona Charging. Acta Physica Sinica, 55, 2464-2469. http://doi.org/10.7498/aps.55.2464
- 14. Min, D., Cho, M., Khan, A.R. and Li, Sh. (2012) Charge Transport Properties of Dielectrics Revealed by Isothermal Surface Potential Decay. IEEE Transactions on Dielectrics and Electrical Insulation, 19, 1465-1473. https://doi.org/10.1109/TDEI.2012.6260024
- 15. Vilitis, O., Titavs, E., Nitiss, E. and Rutkis, M. (2013) Chromophore Poling in Thin Films of Organic Glasses. Latvian Journal of Physics and Technical Sciences, 1, 66-75. https://doi.org/10.2478/lpts-2013-0004
- 16. Borzabadi, E., Vaughan, A.S. and Bailey, A.G. (2003) Electrostatic Surface Potential Decay on Cellulose Acetate. Annual Report Conference on Electrical Insulation and Dielectric Phenomena, Albuquerque, 19-22 October 2003, 193-196.
- 17. Brunson, J. and Dennison, J.R. (2005) Measuring Charge Storage Decay Time and Resistivity of Spacecraft Insulators. All Physics Faculty Publications, 1480. https://digitalcommons.usu.edu/physics_facpub/1480
- 18. Ram, A. (1997) Fundamentals of Polymer Engineering. Springer, Boston, 90. https://doi.org/10.1007/978-1-4899-1822-2
- 19. Warfield, R.W. and Petree, M.C. (1961) Electrical Resistivity of Polymers. Polymer Engineering & Science, 1, 80-85. https://doi.org/10.1002/pen.760010208
- 20. Pallon, L.K.H., et al. (2015) Formation and the Structure of Freeze-Dried MgO Nanoparticle Foams and Their Electrical Behavior in Polyethylene. Journal of Materials Chemistry A, 3, 7523-7534. https://doi.org/10.1039/C4TA06362G



