Journal of Computer and Communications
Vol.04 No.12(2016), Article ID:71671,45 pages
10.4236/jcc.2016.412004
Cryptographic Protocols Based on Nielsen Transformations
Benjamin Fine1, Anja I. S. Moldenhauer2, Gerhard Rosenberger2
1Department of Mathematics, Fairfield University, Fairfield, CT, USA
2Fachbereich Mathematik, Universität Hamburg, Hamburg, Germany
Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: August 14, 2016; Accepted: October 28, 2016; Published: October 31, 2016
ABSTRACT
We introduce in this paper cryptographic protocols which use combinatorial group theory. Based on a combinatorial distribution of shares we present secret sharing schemes and cryptosystems using Nielsen transformations. Nielsen transformations are a linear technique to study free groups and general infinite groups. In addition the group of all automorphisms of a free group F, denoted by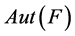 , is generated by a regular Nielsen transformation between two basis of F, and each regular Nielsen transformation between two bases of F defines an automorphism of F.
, is generated by a regular Nielsen transformation between two basis of F, and each regular Nielsen transformation between two bases of F defines an automorphism of F.
Keywords:
Nielsen Transformation, Matrix Group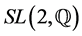 , Secret Sharing Protocol, Private Key Cryptosystem, Public Key Cryptosystem
, Secret Sharing Protocol, Private Key Cryptosystem, Public Key Cryptosystem

1. Introduction
This paper is located in the area of group based cryptography. A cryptographic protocol consists of the collection of rules, formulas and methods to handle a cryptographic task. In cryptology it is common to call the parties who want to communicate privately with each other Alice and Bob.
The traditional cryptographic protocols, both symmetric key and public key, such as the RSA algorithm, Diffie-Hellman and elliptic curve methods, are number theory based. Hence, from a theoretical point of view, they depend on the structure of abelian groups. Although there have been no successful attacks on the standard protocols, there is a feeling that the strength of computing machinery has made the techniques less secure. As a result of this, there has been an active line of research to develop and analyse new cryptographic protocols, as for example cryptosystems and key exchange protocols, based on non-commutative cryptographic platforms. Up to this point the main sources for non-commutative platforms have been nonabelian groups. For an overwiev about mathematical cryptography see [1] and especially for a book about non-commutative group based cryptography see [2] .
Important along the line of cryptographic protocols are secret sharing protocols. These consist of methods to distribute a secret among a group of users by giving a share of the secret to each. The secret can be recovered only if a sufficient number of users (but perhaps not all) combine their pieces. There are many different motivations for the secret sharing problem. One of the most important is the problem of maintaining sensitive information. There are two crucial issues here: availability and secrecy. If only one person keeps the entire secret, then there is a risk that the person might lose the secret or the person might not be available when the secret is needed. Hence it is often useful to utilize several people in order to access a secret. On the other hand, the more people who can access the secret, the higher the chance the secret will be leaked. By sharing a secret in a threshold scheme the availability and reliability issues can be addressed. The paper by C. Chum, B. Fine and X. Zhang [3] contains a wealth of information on secret sharing schemes in general and managing an access control group.
This paper is organized as follows. We first describe secret sharing protocols and a combinatorial distributions of shares, which are given by D. Panagopoulos in [4] . After introductory definitions we start with a secret sharing scheme using directly the combinatorial distribution of shares. Based on this we present two schemes in which we apply regular Nielsen transformations in connections with faithful representations of free groups and the Nielsen reduction theory. We also modify the secret sharing schemes to a private key cryptosystem and finally Nielsen transformations are used for a public key cryptosystem which is inspired by the ElGamal cryptosystem. The new cryptographic protocols are in the dissertation of A. Moldenhauer [5] under her supervisor G. Rosenb-erger at the University of Hamburg. Thus, parts of this paper are from [5] .
2. Preliminaries for the Newly Developed Cryptographic Protocols
A 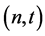 -secret sharing protocol, with
-secret sharing protocol, with  and
and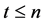 , is a method to distribute a secret among a group of n participants in such a way that it can be recovered only if at least t of them combine their shares. Hence any group of
, is a method to distribute a secret among a group of n participants in such a way that it can be recovered only if at least t of them combine their shares. Hence any group of  or fewer participants cannot calculate the secret. The number t is called threshold. The person who distrib- utes the shares is called dealer.
or fewer participants cannot calculate the secret. The number t is called threshold. The person who distrib- utes the shares is called dealer.
One of the first 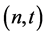 -secret sharing schemes is introduced by A. Shamir in [6] . It has become the standard method for solving the
-secret sharing schemes is introduced by A. Shamir in [6] . It has become the standard method for solving the 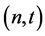 -secret sharing problem.
-secret sharing problem.
A. Shamir uses polynomial interpolation for his 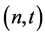 -secret sharing scheme. Let
-secret sharing scheme. Let  be any field and let
be any field and let 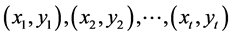 be t points in
be t points in 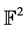 with pairwise distinct
with pairwise distinct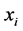 ,
, . We say a polynomial
. We say a polynomial 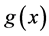 over
over  interpolates these points if
interpolates these points if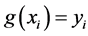 ,
,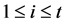 . A. Shamir’s secret sharing scheme is based on the following theorem.
. A. Shamir’s secret sharing scheme is based on the following theorem.
Theorem 1. [7]
Let 







A. Shamir’s 














D. Panagopoulos presents in his paper [4] a 
Share distribution method explained by D. Panagopoulos.
To distribute the shares in a 
1) Calculate

2) Let 





3) The dealer distributes to each of the n participants one of the sets
In addition to this share distribution method the new protocols in this paper are based on combinatorial group theory and Nielsen transformations. Therefore, we review some basic definitions concerning regular Nielsen transformations and Nielsen reduced sets (see [8] or [9] ).
Combinatorial group theory is the branch of algebra which studies groups with the help of group presentations. A group presentation for a group G consists of a set X of generators and a set R of defining relators on X. We write.
The group G is called finitely generated if both sets X and R are finite. The newly developed cryptographic protocols use finitely generated free groups. Let F be a finitely generated free group with free generating set

group F is the set of all reduced words in







The empty space on the right symbolized, that there are only trivial relators. For more information about group theory see for instance [8] , [9] or [10] .
Let F be a finitely generated free group on the free generating set




Definition 2 An elementary Nielsen transformation on 
(T1) replace some 

(T2) replace some 


(T3) delete some 

In all three cases the 

Nielsen transformations are a linear technique to study free groups and general infinite groups. In addition the group of all automorphisms of a free group F, denoted by
Definition 3. A finite set U in F is called Nielsen reduced, if for any three elements 

(N0)
(N1) 

(N2) 


Here 

Proposition 4. ( [8] , Theorem 2.3) or ( [9] , Proposition 2.2)
If 
For the secret sharing schemes based on Nielsen transformations we will only use regular Nielsen transformations. We agree on some notations.
We write 











Corollary 5. ( [8] , Korollar 2.9)
Let F be a free group with basis X and let U be a subset of X which is Nielsen reduced. Then it is

Especially, if U is also a basis for F, then
Theorem 6. ( [8] , Satz 2.6)
Let U be Nielsen reduced, then 
For the next lemma we need some notations. Let 

segment of w is that initial segment 

If the free length of the word w is even, we call the initial segment s of w, with 


Let 


Lemma 7. ( [10] , Lemma 3.1)
Let 


1) Both the major initial and major terminal segments of each 
2) For each 
There are different problems known in combinatorial group Theory, for example:
Theorem 8. ( [8] , Satz 1.9) Isomorphism problem in free groups:
Let X and Y be two sets. Let 


Problem 9. Word problem:
Let 

A further problem, which is a more general problem than the word problem and is needed for some of the developed cryptographic protocols based on combinatorial group theory, is the membership problem or also called extended word problem.
Problem 10. Membership problem:
Given a recursively presented group G, a subgroup H of G generated by
and an element

A related problem (to the membership problem) is the constructive membership problem.
Problem 11. Constructive membership problem:
Given a recursively presented group G, a subgroup H of G generated by 


Theorem 12. ( [8] , Satz 1.9) Isomorphism problem in free groups:
Let X and Y be two sets. Let 


Furthermore, we introduce a linear congruence generator because it is also used for the cryptosystems in this paper.
For 




Definition 13. [1]
Let 



Theorem 14. [1] (Maximal period length for n = 2m,
Let










Then the sequence 

1) 

2) If 

3) 

3. A Combinatorial Secret Sharing Scheme
Now we present a 
The numbers n and t are given, whereby n is the number of participants and t is the threshold.
1) The dealer first calculates the number
2) He chooses m elements


3) Each participant 


If t of the n participants come together they can reconstruct the secret while they first combine their t private sets 

The secret is the sum of the inverse elements in the set

This cryptographic protocol is summarized in Table 1 .
If the dealer needs a special secret 



The participants get 
Security 15. Each element 









Table 1. Summary of the combinatorial 
If just one element 
Remark 16. We realize that the share distribution method by D. Panagopoulos is also given as a special case by M. Ito, A. Saito and T. Nishizeki in [11] . In [5] it is shown that if the method in [11] is used to generate a 

In addition, in [5] it is shown in detail, that the purely combinatorial secret sharing scheme is very similar to a scheme, which J. Benaloh and J. Leichter obtain if they realize a 
Remark 17. It is important in terms of practicability, that the dealer calculates and distributes the shares for the participants long before the secret is needed by the participants. Hence, the dealer has enough time to execute the share distribution method and his computational cost should be of no consequence for the cryptographic protocol. If t participants reconstruct the secret, they add up only m elements, which is feasible in linear time.
Example 18. We perform the steps for a 


The dealer follows the steps:
1) He first calculates
2) The dealer chooses the numbers


(a) The six subsets with size 2 of the set 
With help of the 








3) The dealer distributes the set 


If three of the four participants come together, they can calculate the secret S. For example the participants 

and hence get the secret
4. A Secret Sharing Scheme Using a Regular Nielsen Transformation
In this section we describe a 


We use the special linear group over the rational numbers because these numbers can be stored and computed more efficiently on a computer than irrational numbers.
Let F be a free group in 

distribute the shares for the participants as described in Section 2. The shares will be subsets of a free generating set of the group F (in an abstract and an explicit version).
The numbers n and t are given, whereby n is the number of participants and t is the threshold. The dealer does the following steps:
1) He chooses an abstract free generating set X for the free group F of rank

He also needs an explicit free generating set M, that is

and
2) With the known matrices in the set M he computes the secret




If the dealer needs a special secret he can act as in Section 3 described.
3) The dealer constructs the shares for the participants in the following way:
(a) He first applies a regular Nielsen transformation simultaneously for both sets X and M to get Nielsen-equivalent sets U and N to X and M, respectively (see Figure 1).
The elements 


(b) The dealer now uses the method of D. Panagopoulos to split U and N and to get the shares 


4) The dealer distributes the shares.
If t of the n participants combine their parts they obtain the sets U and N. The secret can be recovered as follows:
1. The participants apply regular Nielsen transformations in a Nielsen reduction manner for U and step by step simultaneously for N. By Proposition 4 they get Nielsen reduced sets 


Because of Corollary 5 it is 









The cryptographic protocol is summarized in Table 2 (page 73).
Less than t participants can neither get the whole set U, which is Nielsen-equivalent to X, nor the set N, which is Nielsen-equivalent to M.
For the calculation of the secret, the participants need the set M, because the secret depends on the traces of the matrices
If the set U is known, it is only known which Nielsen transformation should be done to get the Nielsen-equivalent set X, but it is unknown on which matrices they should be done simultaneously.
If only the set N is known, then the matrices in 
In the book ( [13] , page 247) of J. Lehner a method is given to explicitly obtain a free
Figure 1. Simultaneously regular Nielsen transformations for the dealer.
Figure 2. Simultaneously regular Nielsen transformations for the participants.
Table 2. Summary of the secret sharing scheme using Nielsen transformations and
generating set M for a free group F on the abstract generating set
Theorem 19. [13] Let F be a free group with countably many free generators


with 

The group G generated by 
We now present an example for this secret sharing scheme.
Example 20. We perform the steps for a 
of the computer program Maple 16. It is


First the Dealer generates the shares for the participants.
1) The dealer chooses an abstract presentation for the free group F of rank 3
He takes an explicit presentation

and hence the set of the matrices
is a free generating set for a free group of rank 3.
2) The dealer chooses
and hence the secret is
3) Construction of the shares for the participants:
(a) First the dealer applies regular Nielsen transformations (NTs) simultaneously for both sets X and M to get Nielsen-equivalent sets U and N to X and M, respectively. These transformations are shown in Table 3 (see page 75) and Table 4 (see page 76).
The Dealer obtains the sets
and
(b) He gets the shares 


Table 3. Nielsen transformations (NTs) of the dealer I.
Table 4. Nielsen transformations (NTs) of the dealer II.
i) It is
ii) The dealer chooses the elements 
With the help of the 








Now we apply this to U and N to create the share-sets for the participants, respec- tively:
4) The Dealer distributes to each participant a tuple






Assume the participants 



The participants apply regular Nielsen transformations step by step simultaneously for both sets U and N to get 

With the knowledge of the set 
Table 5. Nielsen transformations (NTs) from the participants I.
and hence it is
In general we can use any free matrix group F of rank 







Table 6. Nielsen transformations (NTs) from the participants II.
5. Another Secret Sharing Scheme Based on Nielsen Transformations
We explain another secret sharing scheme which arises of the protocol in Section 4. As in the previous section, let F be a finitely generated free group with the abstract free generating set

For a 




with 

The dealer does a regular Nielsen transformation on the set U to get the Nielsen- equivalent set V (see Figure 3).
Each participant


Figure 3. Regular Nielsen transformation.
If t of the n participants come together to reconstruct the secret, they combine their shares and get the set



because for each i it is 


This 
6. A Symmetric Key Cryptosystem Using Nielsen Transformations
In this section we introduce a symmetric key cryptosystem using Nielsen transfo- rmations. Before Alice and Bob are able to communicate with each other, they have to make some arrangements.
We speak about public parameters also in private key cryptosystems, because these are parameters which each person, also an eavesdropper, Eve, gets, if she looks at the sent ciphertext. Public parameters are also elements, which Alice and Bob communicate with each other publicly. It is also not a secret which plaintext alphabet is used for the communication.
Public Parameters.
They first agree on the following public parameters.
1) A finitely generated free group F with free generating set 

2) A plaintext alphabet 

3) An abstract free group 




4) A subset 



Table 7. Summary of the 
The set 
5) They agree on a linear congruence generator 
Private Parameters.
Now, they agree on the private parameters.
1) Alice and Bob choose an explicit Nielsen reduced set U with N elements, which are words in X. Such systems U are easily to construct (see Lemma 7 and Theorem 6 or also [8] and [9] ).
Now, it is 

2) They use a one-to-one correspondence

3) Alice and Bob agree on an automorphism






Remark 21. If the explicit set





The key space: The set 


Private Key Cryptosystem.
Now, we explain the private key cryptosystem and look carefully at the steps for Alice and Bob.
Public knowledge:





Encryption and Decryption Procedure:
1) Alice and Bob agree privately on the private parameters: a set 

2) Alice wants to transmit the message

with 
2.1) She generates with the linear congruence generator h and the knowledge of 





2.2) The encryption is as follows.

Recall that the one-to-one correspondence 



is sent to Bob. The 











3) Bob gets the ciphertext

with



3.1.a) With the knowledge of




with 

With the knowledge of the Table 8 (page 82) the decryption is as follows

He generates the plaintext message

with
3.1.b) Bob knows the Nielsen reduced set U, hence with an algorithm as for example explained in the book ( [8] , page~33) he is able to write the elements 










This cryptographic protocol is summarized in Table 9 (page 83).
Table 8. Plaintext alphabet 


Remark 22. As soon as Alice and Bob agree on the starting seed automorphism and the Nielsen reduced set U, Bob is able to calculate the first columns of Table 8 (page 82) for decryption (he does not know how many columns he will need because he does not know yet how long the plaintext from Alice will be). If he gets the ciphertext C from Alice, he only has to do a search in the table to get the corresponding plaintext units to
Table 9. Summary of the private key cryptosystem.
the ciphertext units. If columns are missing to decrypt the ciphertext, he calculates the missing columns. Thus, in Version 3.1.a. instead of Version 3.1.b. for decryption Bob is able to do calculations for decryption even before he knows the ciphertext.
Remark 23. The cryptosystem is a polyalphabetic system, that means, a word

It follows an example, in which for decryption a table (see Table 8 (page 82)) is used, which stores the ciphertext alphabet 
Additionally, in [5] an example is given, in which Bob knows the Nielsen reduced set U, hence with a known algorithm he is able to write the ciphertext as a sequence of words in U. With the automorphisms Alice uses for encryption he is able to decrypt the ciphertext correctly.
Example 24. This example was executed in GAP1. All details are given in Appendix A. Firstly, Alice and Bob agree on public parameters.
1) Let F be the free group on the free generating set
2) Let 
3) Let H be the abstract free group of rank 

4) A set 
5) The linear congruence generator with maximal periodic length is
The private parameters for this example are the following:
1) Let 

The starting automorphism 






We now look at the encryption and decryption procedure for Alice and Bob.
2) With the above agreements Alice is able to encrypt her message
Her message is of length 4. She generates the ciphertext as follows:
2.1) First, she determines, with the help of the linear congruence generator 




The automorphisms are describable with the help of regular Nielsen transformations, it is


the Nielsen transformations are applied from the left to the right.
2.2) Secondly, she encrypts her message. The ciphertext is
The ciphertext C is written as words in X, it is
3) Bob gets the ciphertext
from Alice. Thus, he knows that he needs 4 automorphisms for decryption.
3.1) Bob knows the set U, the linear congruence generator h and the starting seed automorphism
Now, he is able to compute for each automorphism 


With these tables he is able to reconstruct the plaintext from Alice. He searches for the plaintext element 





Table 10. Correspondence: Plaintext alphabet to ciphertext alphabet I.
Table 11. Correspondence: Plaintext alphabet to ciphertext alphabet II.
Security 25. The cryptosystem is a polyalphabetic system, that means, a word

The security depends on the fact, that the set U is private. Note, that the ciphertext units 




and 

The symbol “


Let

be the set of ciphertext units and let 

group



main security certification depends on the fact, that for a single subset V of 





A subset of V is also known, it is 

hence a candidate for U.
Furthermore, the security depends on the way how Alice and Bob choose the automorphisms of the set




A more detailed cryptographical analysis can be found in [5] and there are also three modifications given, which are summarized as follows:
1) We present a modification where the ciphertext is only one reduced word in X instead of a sequence of words, in this case it is possible that additional information is needed for decryption, thus these are sent with the ciphertext if required. The ciphertext can be interpreted as words in X and as words in U, thus the additional information could be given about the ciphertext written as a word in U or as a word in X.
Security: The security certification is extended to the fact that Eve is in general not able to identify the beginning and end of a ciphertext unit




2) We present a modification, which uses a faithful representation from F into the special linear group 

Security: The security certification is extended to the fact, that there is no algorithm known to solve the (constructive) membership problem for (discrete) free subgroups of 


3) We present a modification, which utilizes the negative solution of Hilbert's Tenth Problem. Instead of a presentation of the ciphertext as a sequence of matrices in 



Security: The security certification is extended to Hilbert’s Tenth Problem. In addition the security is improved by the fact, that for each encryption Alice and Bob can take privately ephemeral matrices in




Remark 26. In [5] are two more private key cryptosystems given, which use finitely generated free groups, Nielsen transformations and automorphisms on finitely generated free group. The first one uses automorphisms on F instead of a subgroup of F, as in the above described private key cryptosystem. It also has three modifications, which use the ideas for the modifications above. The second protocol uses automo- rphisms on plaintext units and in addition randomly chosen ephemeral keys (matrices of
7. Cryptosystem with Nielsen Transformation Inspired by the ElGamal Cryptosystem
Now we describe a public key cryptosystem for Alice and Bob which is inspired by the ElGamal cryptosystem (see [16] or ( [2] , Section 1.3)), based on discrete logarithms, that is:
1) Alice and Bob agree on a finite cyclic group G and a generating element
2) Alice picks a random natural number a and publishes the element
3) Bob, who wants to send a message 



4) Alice recovers
For the new public key cryptosystem in this section let







An ElGamal like public key cryptosystem, with public parameters determined by Alice, is now as follows:
Public parameters: The finitely generated free group


Encryption and Decryption Procedure:
1) Alice chooses privately a natural number n and publishes the element
2) Bob picks privately a random 


He sends the ciphertext 
3) Alice calculates

and gets the message m.
The ElGamal like public key cryptosystem is summarized in Table 12 (page 90).
Remark 27. It is important that different random ephemeral keys t are used to encrypt different messages. As it is for the standard ElGamal cryptosystem (see [18] ). Suppose that Bob uses the same ephemeral key t to encrypt two messages 









Security 28. A possible attacker, Eve, can see the elements






Table 12. Summary of the ElGamal like public key cryptosystem using automorphisms on a finitely generated free group F.
in the free generating set X from which it is unlikely to realize the exponents n and t, that is, the private keys from Alice and Bob, respectively. The security is based on the Diffie-Hellman problem and discrete logarithm problem in cyclic subgroups of automorphisms in free groups.
Variation 29. We give some ideas to enhance the security, they can also be combined:
1) The element 
2) Alice and Bob agree on a faithful representation from F into the special linear group
of all 









We now explain this variation in more details.
In addition to 










Alice needs a faithful representation of 



Thus, each 

(a) The public element from Alice is as before

(b) Bob chooses privately a message


and writes it as a word in Y whereby he used the assignment 








Instead of 

(c) Firstly, Alice calculates 

Bob, because

Secondly, she writes 




She gets a matrix in 




An eavesdropper, Eve, gets a matrix 





We now end this section with an example.
Example 30. This example, is a very small one and it is just given for illustration purposes. The calculations were done with GAP, see Appendix B. Bob wants to send a message to Alice.
The public parameters are the free group F of rank 3 with free generating set




1) Alice’s private key is
Her public key is
2) Bob privately picks the ephemeral key 
His message for Alice is
and
The ciphertext for Alice is the tuple
3) Alice first computes
and gets m by
8. Conclusions
A. Shamir’s secret sharing protocol (see [6] ) has become the standard method for solving the 
In contrast to other secret sharing schemes the part for the participants at the combinatorial secret sharing scheme, see Section 3, is very easy, they only have to add up m elements. The (time) expensive part is the part of the dealer, who has to generate the sets 
The secret sharing scheme of Section 4 uses combinatorial group theory, especially Nielsen transformations and finitely generated free groups. It is mathematically a very interesting cryptographic protocol, which serves very good as a basis to develop other cryptographic protocol. In addition the secret sharing scheme of Section 5 is also a mathematically very interesting cryptographic protocol. Both secret sharing schemes are the basis for the newly developed cryptosystems.
In comparison to the standard cryptosystems which are mostly based on number theory we explained two cryptosystems which use combinatorial group theory. The first cryptosystem in Section 6 is a kind of a one-time pad, which choice of the random sequence for encryption is not number-theoretic. Especially the modifications with matrices are of interest for cryptography. If the symmetric key cryptosystem is used together with the second modification, which uses a faithful representation into




For further research one could search for other cryptographic protocols, which can be based on Nielsen transformations, for example a public key cryptosystem which is not ElGamal like or a key exchange protocol. There is no algorithm known to solve the (constructive) membership problem for (discrete) free subgroups of rank equal or greater than 2 in

Cite this paper
Fine, B., Moldenhauer, A.I.S. and Rosenberger, G. (2016) Cryp- tographic Protocols Based on Nielsen Trans- formations. Journal of Computer and Com- munications, 4, 63-107. http://dx.doi.org/10.4236/jcc.2016.412004
References
- 1. Baumslag, G., Fine, B., Kreuzer, M. and Rosenberger, G. (2015) A Course in Mathematical Cryptography. De Gruyter, Berlin.
http://dx.doi.org/10.1515/9783110372779 - 2. Myasnikov, A., Shpilrain, V. and Ushakov, A. (2008) Group-Based Cryptography. Advanced Courses in Mathematics - CRM Barcelona. Birkhäuser, Basel.
- 3. Chum, C., Fine, B. and Zhang, X. Shamir’s Threshold Scheme and Its Enhancements. To Appear.
- 4. Panagopoulos, D. (2010) A Secret Sharing Scheme Using Groups. Preprint.
http://arxiv.org/abs/1009.0026 , - 5. Moldenhauer, A.I.S. (2016) Cryptographic Protocols Based on Inner Product Spaces and Group Theory with a Special Focus on the Use of Nielsen Transformations. Ph.D. Thesis, University of Hamburg, Hamburg.
- 6. Shamir, A. (1979) How to Share a Secret. Communications of the ACM, 22, 612-613.
- 7. Atkinson, K. (1989) An Introduction to Numerical Analysis. 2nd Edition, John Wiley & Sons, Hoboken.
- 8. Camps, T., Groβe Rebel, V. and Rosenberger, G. (2008) Einführung in die kombinatorische und die geometrische Gruppentheorie. Berliner Studienreihe zur Mathematik Band 19. Heldermann Verlag, Berlin.
- 9. Lyndon, R.C. and Schupp, P.E. (1977) Combinatorial Group Theory. Ergebnisse der Mathematik und ihre Grenzgebiete 89, Springer-Verlag, New York.
- 10. Magnus, W. Karrass, A. and Solitar, D. (1966) Combinatorial Group Theory. Pure and Applied Mathematics, a Series of Texts and Monographs Volume XIII. John Wiley & Sons, Hoboken.
- 11. Ito, M., Saito, A. and Nishizeki, T. (1987) Secret Sharing Scheme Realizing General Access Structure. Proceedings of IEEE Globecom 87, 99-102.
- 12. Benaloh, J. and Leichter, J. (1990) Generalized Secret Sharing and Monotone Functions. CRYPTO '88. Springer-Verlag, New York.
- 13. Lehner, J. (1964) Discontinuous Groups and Automorphic Functions. Mathematical Surveys Number VIII. American Mathematical Society, Providence.
http://dx.doi.org/10.1090/surv/008 - 14. GAP (2015) Version 4.7.7 of 13-feb-2015 (Free Software, GPL).
http://www.gap-system.org - 15. Eick, B., Kirschmer, M. and Leedham-Green, C. (2014) The Constructive Membership Problem for Discrete Free Subgroups of Rank 2 of . LMS Journal of Computation and Mathematics, 17, 345-359.
http://dx.doi.org/10.1112/S1461157014000047 - 16. ElGamal, T. (1985) A Public Key Cryptosystem and a Signature Scheme Based on Discrete Logarithms. IEEE Transactions on Information Theory, IT-31, 469-473.
http://dx.doi.org/10.1109/TIT.1985.1057074 - 17. Diekert, V., Kufleitner, M. and Rosenberger, G. (2013) Diskrete algebraische Methoden. De Gruyter, Berlin.
http://dx.doi.org/10.1515/9783110312614 - 18. Menezes, A.J., van Oorschot, P.C. and Vanstone, S.A. (1997) Handbook of Applied Cryptography. CRC Press LLC, Boca Raton.
Appendix
We now give the computer code in GAP2 for Example 24 and Example 30. Therefore we use the FGA3 package in GAP and also Nielsen transformations.
If there are Nielsen transformations of type 


the following
A. Calculations in GAP for Example 24
Alice and Bob use the free group




In GAP they define
LoadPackage("FGA");;
F:=FreeGroup("x", "y", "z");;
AssignGeneratorVariables(F);;
u1:=x*y*z;;
u2:=y*z*y^-1;;
u3:=x^-1*z*x^-1;;
u4:=y^-1*x^2;;
u5:=z^-1*x*y*x;;
u6:=z^-1*y*x^-1;;
u7:=x^3*y;;
u8:=y^3*z^-2;;
FU:=Group(u1, u2, u3, u4, u5, u6, u7, u8);;
and prove that U is a Nielsen reduced set with the operation
> FreeGeneratorsOfGroup(FU)
which gives a Nielsen reduced generator set for the group FU:
gap> Free Generators Of Group (FU);
[x*y*z, y*z*y^-1, x^-1*z*x^-1, y^-1*x^2, z^-1*x*y*x,\
z^-1*y*x^-1, x^3*y, y^3*z^-2 ]
Alice knows the linear congruence generator h hence she can get the 4 required automorphisms of the set 
These automorphisms are describable with Nielsen transformations as follows:
Automorphism
Hence, the automorphism is
Automorphism
Hence, the automorphism is
Automorphism
Hence, the automorphism is
Automorphism
Hence, the automorphism is
In GAP she defines for the automorphisms:
#Automorphism f_{u_1}
u11:=u1*u7*u2*u4;;
u12:=u2*u4*u3*u4^2;;
u13:=u3*u4^2;;
u14:=u4*u6*u5^-1*u1*u7;;
u15:=u5^-1*u1*u7;;
u16:=u6*u3*u4^2;;
u17:=u6^-1*u4^-1*u7*u8;;
u18:=u8*u1*u7;;
#Automorphism f_{u_2}
u21:=u3^-1*u1^-1*u2*u4;;
u22:=u2^-1*u8*u6*u5;;
u23:=u3*u5*u4^-2;;
u24:=u2*u4*u7*u6*u5;;
u25:=u5*u2^-1*u6*u5;;
u26:=u6*u5*u2*u4;;
u27:=u7*u6*u5;;
u28:=u8*u4^-1*u2^-1;;
#Automorphism f_{u_3}
u31:=u1*u2^-1*u7^-1*u3^-1*u8;;
u32:=u2^-1*u3*u7;;
u33:=u3*u7*u4*u8^-2;;
u34:=u4*u8^-2;;
u35:=u5^-1*u6*u3;;
u36:=u6*u2^3*u7;;
u37:=u7*u4*u8^-2;;
u38:=u7^-1*u3^-1*u8;;
#Automorphism f_{u_4}
u41:=u4*u3*u1;;
u42:=u3*u2^-1*u4*u3;;
u43:=u4*u3*u5*u2*u3^-1;;
u44:=u4^-1*u5*u2*u3^-1;;
u45:=u5*u2*u3^-1;;
u46:=u6*u2*u4*u3*u1;;
u47:=u7*u4^-1*u3*u2^-1;;
u48:=u8*u2^3*u3^-1*u4^-1;;
Hence, to get the ciphertext
as a word in X, she calculates in GAP:
gap > u11;
x*y*z*x^3*y^2*z*y^-2*x^2
gap> u24;
y*z*y^-2*x^5*y*z^-1*y*x^-1*z^-1*x*y*x
gap> u37;
x^5*(z^2*y^-3)^2
gap> u42;
x^-1*z*x^-1*y*z^-1*y^-2*x*z*x^-1
Thus, the ciphertext is
and this is sent to Bob.
For decryption Bob calculates the tables Table 10 (page 86) and Table 11 (page 87). For this he chooses the automorphisms in
gap> u11; u12; u13; u14; u15; u16; u17; u18;
x*y*z*x^3*y^2*z*y^-2*x^2
y*z*y^-2*x*z*x^-1*(y^-1*x^2)^2
x^-1*z*x^-1*(y^-1*x^2)^2
y^-1*x^2*z^-1*y*x^-2*y^-1*x^-1*z*x*y*z*x^3*y
x^-1*y^-1*x^-1*z*x*y*z*x^3*y
z^-1*y*x^-2*z*x^-1*(y^-1*x^2)^2
x*y^-1*z*x^-2*y*x^3*y^4*z^-2 y^3*z^-2*x*y*z*x^3*y
gap> u21; u22; u23; u24; u25; u26; u27; u28;
(x*z^-1)^2*y^-1*x^-1*y*z*y^-2*x^2
y*z^-1*y^2*z^-3*y*x^-1*z^-1*x*y*x
x^-1*z*x^-1*z^-1*x*(y*x^-1)^2*x^-1*y
y*z*y^-2*x^5*y*z^-1*y*x^-1*z^-1*x*y*x z^-1*(x*y)^2*z^-1*y^-1*z^-1*y*x^-1*z^-1*x*y*x z^-1*y*x^-1*z^-1*(x*y)^2*z*y^-2*x^2
x^3*y*z^-1*y*x^-1*z^-1*x*y*x
y^3*z^-2*x^-2*y^2*z^-1*y^-1
gap> u31; u32; u33; u34; u35; u36; u37; u38;
x*y*z*y*z^-1*y^-2*x^-2*z^-1*x*y^3*z^-2
y*z^-1*y^-1*x^-1*z*x^2*y
x^-1*z*x^4*(z^2*y^-3)^2
y^-1*x^2*(z^2*y^-3)^2
x^-1*y^-1*x^-1*y*x^-2*z*x^-1
z^-1*y*x^-1*y*z^3*y^-1*x^3*y
x^5*(z^2*y^-3)^2
y^-1*x^-2*z^-1*x*y^3*z^-2
gap> u41; u42; u43; u44; u45; u46; u47; u48;
y^-1*x*z*y*z
x^-1*z*x^-1*y*z^-1*y^-2*x*z*x^-1
y^-1*x*z*x^-1*z^-1*(x*y)^2*z*y^-1*x*z^-1*x x^-2*y*z^-1*(x*y)^2*z*y^-1*x*z^-1*x
z^-1*(x*y)^2*z*y^-1*x*z^-1*x
z^-1*y*x^-1*y*z*y^-2*x*z*y*z
x^3*y*x^-2*y*x^-1*z*x^-1*y*z^-1*y^-1
y^3*z^-2*y*z^3*y^-1*x*z^-1*x^-1*y
With this information Bob is able to reconstruct the message
B. Calculations in GAP for Example 30
Alice defines the public parameters.
Let 
LoadPackage("FGA");;
F:=FreeGroup("x", "y", "z");;
AssignGeneratorVariables(F);;
Additionally she defines the freely reduced word 
hence the automorphism is
and she defines in GAP:
x1:=x*y^2;;
y1:=z^(-1);;
z1:=y^(-1)*z^(-1);;
Alice chooses as private key

#Calculate automorphism f^2=f^1(f^1)
x2:=x1*y1^2;;
y2:=z1^(-1);;
z2:=y1^(-1)*z1^(-1);;
gap> x2; y2; z2;
x*y^2*z^-2
z*y
z^2*y
#Calculate automorphism f^3=f^1(f^2)
x3:=x2*y2^2;;
y3:=z2^(-1);;
z3:=y2^(-1)*z2^(-1);;
gap> x3; y3; z3;
x*y^2*z^-1*y*z*y
y^-1*z^-2
(y^-1*z^-1)^2*z^-1
#Calculate automorphism f^5=f^2(f^3)
x5:=x3*y3^2*z3^(-2);;
y5:=z3*y3;;
z5:=z3^2*y3;;
gap> x5; y5; z5;
x*y^2*z^-1*y^2*z*(z*y)^2
y^-1*(z^-1*y^-1*z^-1)^2*z^-1
((y^-1*z^-1)^2*z^-1)^2*y^-1*z^-2
#Calculate automorphism f^7=f^2(f^5)
x7:=x5*y5^(2)*z5^(-2);;
y7:=z5*y5;;
z7:=z5^2*y5;;
gap> x7; y7; z7;
x*y^2*z^-1*y*(y*z)^2*(z*y*z^2*y)^2*z*y y^-1*((z^-1*y^-1*z^-1)^2*y^-1*z^-1)^2*z^-1*y^-1*z^-2 (((y^-1*z^-1)^2*z^-1)^2*y^-1*z^-2)^2*y^-1*(z^-1*y^-1*z^-1)^2*z^-1
Thus, the automorphism 
Her public key is
c:=x7^2*y7*z7^(-2)*y7;;
gap> c;
(x*y^2*z^-1*y*(y*z)^2*(z*y*z^2*y)^2*z*y)^2*(z^2*y)^2*\ ((z*y*z)^2*y*z)^2*z*y*z^2*y*z^-1
Bob is now able to send a message to Alice. Let 


m:=z^-2*y^2*z*x^2*y^-1*x^-1;;
#Calculate automorphism f^2=f^1(f^1)
x2:=x1*y1^2;;
y2:=z1^(-1);;
z2:=y1^(-1)*z1^(-1);;
gap> x2; y2; z2; x*y^2*z^-2 z*y z^2*y
#Calculate automorphism f^3=f^1(f^2)
x3:=x2*y2^2;;
y3:=z2^(-1);;
z3:=y2^(-1)*z2^(-1);;
gap> x3; y3; z3;
x*y^2*z^-1*y*z*y
y^-1*z^-2
(y^-1*z^-1)^2*z^-1
#Calculate automorphism f^5=f^2(f^3)
x5:=x3*y3^2*z3^(-2);;
y5:=z3*y3;;
z5:=z3^2*y3;;
gap> x5; y5; z5;
x*y^2*z^-1*y^2*z*(z*y)^2
y^-1*(z^-1*y^-1*z^-1)^2*z^-1
((y^-1*z^-1)^2*z^-1)^2*y^-1*z^-2
Hence, the automorphism 
He now calculates his ciphertext 


#c22:=f^5(c)
c22:=(x5*y5^2*z5^(-1)*y5*(y5*z5)^2*(z5*y5*z5^2*y5)^2*z5*y5)^2*\ (z5^2*y5)^2*((z5*y5*z5)^2*y5*z5)^2*z5*y5*z5^2*y5*z5^(-1);;
c1:=m*c22;;
gap> c1;
z^-2*y^2*z*x^2*(y*z^-1)^2*((z^-1*y^-1*z^-2*y^-1)^2\ *z^-2*y^-1)^2*(z^-1*y^-1*z^-1)^2*z^-1*y^-1*((((z^-\ 1*y^-1*z^-1)^2*y^-1*z^-1)^2*z^-1*y^-1*z^-1*y^-1*z^\ -1)^2*(z^-1*y^-1*z^-2*y^-1)^2*z^-1*y^-1*z^-1)^2*((\ z^-1*y^-1*z^-2*y^-1)^2*z^-2*y^-1)^2*(z^-1*y^-1*z^-\ 1)^2*z^-1*x*y^2*z^-1*y*(z^-1*(((z^-1*y^-1*z^-2*y^-\ 1)^2*z^-2*y^-1)^2*(z^-1*y^-1*z^-1)^2*z^-1*y^-1)^3*\ (z^-1*y^-1*z^-1)^2*y^-1*z^-1*((z^-1*y^-1*z^-2*y^-1\
)^2*z^-2*y^-1)^2*(z^-1*y^-1*z^-1)^2*y^-1)^3*z^-1*(\ (z^-1*y^-1*z^-2*y^-1)^2*z^-2*y^-1)^2*(z^-1*y^-1*z^-1)^2*\
y^-1*z^-1*y
#c2:=f^5(a)
c2:=x5^2*y5*z5^(-2)*y5;;
gap> c2;
(x*y^2*z^-1*y^2*z*(z*y)^2)^2*z^2*y*(z*y*z)^2*z*y*z^-1
Bob sends 
In GAP she computes:
#dc:=f^7(c2)
dc:=(x7*y7^2*z7^(-1)*y7^2*z7*(z7*y7)^2)^2*z7^2*y7*\ (z7*y7*z7)^2*z7*y7*z7^(-1);;
gap> dc;
(x*y*(y*z^-1)^2*((z^-1*y^-1*z^-2*y^-1)^2*z^-2*y^-1\
)^2*(z^-1*y^-1*z^-1)^2*z^-1*y^-1*((((z^-1*y^-1*z^-\ 1)^2*y^-1*z^-1)^2*z^-1*y^-1*z^-1*y^-1*z^-1)^2*(z^-\ 1*y^-1*z^-2*y^-1)^2*z^-1*y^-1*z^-1)^2*((z^-1*y^-1*\ z^-2*y^-1)^2*z^-2*y^-1)^2*(z^-1*y^-1*z^-1)^2*z^-1)\ ^2*y^-1*(((z^-1*y^-1*z^-1)^2*y^-1*z^-1)^2*z^-1*y^-\ 1*z^-1*y^-1*z^-1)^2*(z^-1*y^-1*z^-2*y^-1)^2*z^-1*y\ ^-1*z^-1*((((z^-1*y^-1*z^-2*y^-1)^2*z^-2*y^-1)^2*(\ z^-1*y^-1*z^-1)^2*z^-1*y^-1)^2*((z^-1*y^-1*z^-1)^2\ *y^-1*z^-1)^2*z^-1*y^-1*z^-2*y^-1)^2*(((z^-1*y^-1*\ z^-1)^2*y^-1*z^-1)^2*z^-1*y^-1*z^-1*y^-1*z^-1)^2*(\ z^-1*y^-1*z^-2*y^-1)^2*z^-1*y^-1*z^-1*y
gap> dc^-1;
y^-1*(((((z*y)^2*z)^2*z*y*z)^2*z*y*(z*y*z)^2)^2*z*\ y*((z*y*z)^2*y*z)^2*z*y*z)^2*(z*y*(((z*y*z)^2*y*z)\ ^2*z*y*z*y*z)^2*(z*y*z^2*y)^2*z)^2*y*(((((z^2*y)^2\ *z*y)^2*z^2*y*z*y)^2*z*(z*y*z^2*y)^2*z*y)^2*z*(z*y\ *z^2*y)^2*z^2*y*(((z*y*z)^2*y*z)^2*z*y*z*y*z)^2*(z\ *y*z^2*y)^2*z*(z*y^-1)^2*y^-1*x^-1)^2
gap> c1*dc^-1;
z^-2*y^2*z*x^2*y^-1*x^-1
Finally, she reconstructs the correct message
NOTES
1Groups, Algorithms and Programming [14] .
2Groups, Algorithms and Programming [14] .
3Free Group Algorithms. A GAP4 Package by Christian Sievers, TU Braunschweig.





























































































































































