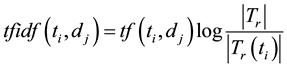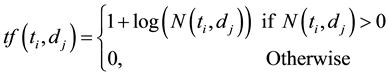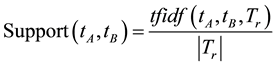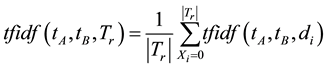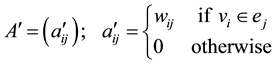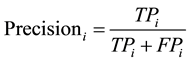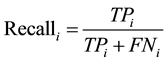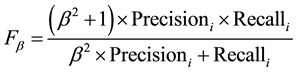Journal of Computer and Communications
Vol.03 No.12(2015), Article ID:61764,13 pages
10.4236/jcc.2015.312004
Document Clustering Using Semantic Cliques Aggregation
Ajit Kumar1, I-Jen Chiang2,3
1Goa Institute of Management, Ribandar, India
2School of Management, Taipei Medical University, Taiwan
3Institute of Biomedical Engineering, National Taiwan University, Taiwan

Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).


Received 30 October 2015; accepted 5 December 2015; published 8 December 2015

ABSTRACT
The search engines are indispensable tools to find information amidst massive web pages and documents. A good search engine needs to retrieve information not only in a shorter time, but also relevant to the users’ queries. Most search engines provide short time retrieval to user queries; however, they provide a little guarantee of precision even to the highly detailed users’ queries. In such cases, documents clustering centered on the subject and contents might improve search results. This paper presents a novel method of document clustering, which uses semantic clique. First, we extracted the Features from the documents. Later, the associations between frequently co-occurring terms were defined, which were called as semantic cliques. Each connected component in the semantic clique represented a theme. The documents clustered based on the theme, for which we designed an aggregation algorithm. We evaluated the aggregation algorithm effectiveness using four kinds of datasets. The result showed that the semantic clique based document clustering algorithm performed significantly better than traditional clustering algorithms such as Principal Direction Divisive Partitioning (PDDP), k-means, Auto-Class, and Hierarchical Clustering (HAC). We found that the Semantic Clique Aggregation is a potential model to represent association rules in text and could be immensely useful for automatic document clustering.
Keywords:
Document Clustering, Semantic Clique, Association, Aggregation, Theme

1. Introduction
The explosion of diverse information over the Internet created a need for the automated tools to help web users find relevant information [1] -[3] . The search engines are indispensable tools to find, filter, and extract the desired information embedded in massive web pages and documents over the Internet [3] . However, the search engines often return inconsistent, irrelevant and messy results [4] . The polysemy, phrases, and term dependency bring additional challenges for search-related technologies [5] . A single term is usually not enough to identify the theme (also known as concept) in the documents. For example, we can associate the term mouse with a computer or animal or person to denote different themes.
The researchers are intermittently upgrading the information searching tools by deploying various concepts such as text mining, machine learning and web-agents [6] -[9] . A good search engine takes care of mainly two aspects. First, the retrieved piece of information must be relevant to users’ queries. Secondly, the information should be retrieved in a shorter time. Most of the search engines take care of the second aspect by providing a speedy response to user queries; however, they provide a little guarantee on the precision (relevance) to users’ queries. In such situations, the subject, and contents based document clustering might improve search results. The clustering discovers the latent themes to organize, summarize, and disambiguate a large collection of web documents [10] [11] . Therefore, document clustering is a potential approach to deal with the diverse and a large number of information presents over the Internet [12] [13] . In the document clustering, a document is viewed as a feature vector point in the multidimensional space. The methods such as the k-Means, Hierarchical Clustering (HCA), Auto Class, and Principal Direction Divisive Partitioning (PDDP) select a set of key Terms/Phrases to organize the feature vectors in different documents [14] -[17] . Most of these methods classify documents from the matrix representation; however, the matrix operations cannot discover all term associations. Also, these approaches consider the co-occurrence of terms but neglect whether terms co-occur in the same context. For example, two terms Wall and Street do not represent a meaningful theme, say Wall Street if these are present at different places in a document. Sometimes, the number of features is exceptionally large, and we extract only the salient features. The frameworks to reduce the dimension of the feature space include term co-occurrence, principal component analysis, independent component analysis, and latent semantic indexing. However, the leftover dimensions can still be enormous, and the quality of the resulting clusters tends to be not good due to the loss of some relevant features. The feature extraction might also result in degradation of cluster quality due to the presence of noise in the data. Automatic query expansion may help the users by adding appropriate words to a query; however, the diversity of topics within a document makes irrelevant data also available to the users’ queries.
We observed the context associations in a collection of documents form a clique [18] . The nodes in the clique correspond to the term in the collection of documents, and the hyperedge connecting one or more nodes indicates support strength in associating the terms involved. The term is defined as a set of words or phrases to define term association formally. Each term can be an empty set or a set of word combinations. The word is a so- called primitive semantic unit in a dictionary. We conjectured that such a clique must have captured the theme of the document collection, and cliques could be aggregated semantically. Therefore, we designed an algorithm for semantic aggregation of the clique (hereafter Semantic Clique Aggregation, SCA in short) based upon the strength of support. Also, we validated if the SCA represented a significant improvement over the traditional methods such as PDDP, k-means, Auto Class and HAC [15] [16] .
2. Methods
We used text-mining concepts such as feature extraction and association and then designed Semantic Clique Aggregation (SCA) algorithm. The algorithm was evaluated by using the four different datasets. This study included the following steps: 1) Feature extraction, 2) Feature association, 3) Semantic clique, 4) Design of Semantic Clique Aggregation algorithm, 5) Evaluation of the algorithm-Dataset and Evaluation criteria.
2.1. Feature Extraction
The feature extraction extracts the key terms from a collection of indexed documents. The document indexing is originally the task of assigning terms to the documents for retrieval. In the earlier approaches, an indexing model was developed based on the assumption that a document should be assigned to these terms that were used by queries, and to which the document was relevant [19] [20] . The 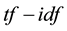 weighted schema was used for information retrieval, where
weighted schema was used for information retrieval, where 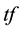 denotes term frequency that appears in the document; and
denotes term frequency that appears in the document; and 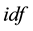 denotes inverse document frequency, where document frequency is the number of documents that contain the term [21] - [23] . The
denotes inverse document frequency, where document frequency is the number of documents that contain the term [21] - [23] . The 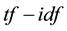 function demonstrates: 1) rare terms are no less prominent than frequent terms according to their values; 2) multiple occurrences of a term in a document are no less significant than singleoccurrence according to their
function demonstrates: 1) rare terms are no less prominent than frequent terms according to their values; 2) multiple occurrences of a term in a document are no less significant than singleoccurrence according to their 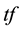 values [24] . Therefore,
values [24] . Therefore, 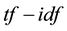 implies the significance of a term in a document. The
implies the significance of a term in a document. The 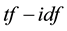 can be defined as follows.
can be defined as follows.
Definition 1 Let 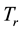 represent a collection of documents. The significance of a term
represent a collection of documents. The significance of a term 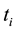 in a document
in a document 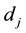 in t
in t 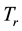 isits
isits 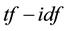 value calculated by the function
value calculated by the function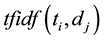 , which is equivalent to the value
, which is equivalent to the value
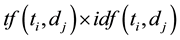 . The value of
. The value of 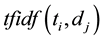 can be calculated as:
can be calculated as:
where 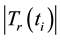
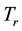
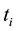
where 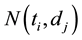
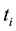
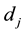
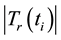
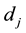
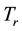
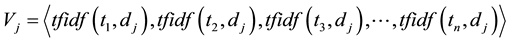
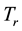
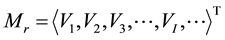
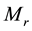
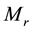
2.2. Feature Association
Support and Confidence are used for defining association rules [28] . We proposed a straightforward idea on association rules in the document clustering, which included only the concept of support. The features use various association rules and algorithms to determine relationships among the features. All documents need to be stored in the intermediate indexed form before performing association analysis of a collection of documents. In the document clustering, when a set of term co-occurred, it represents a theme. The documents containing these terms could be organized as a semantic clique. In this study’s framework, the association rules were determined by the support, whereas confidence was considered as unnecessary. The support for a collection of documents is defined below. Let 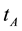
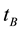
Definition 2 Support denotes the significance of the documents in 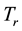
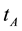
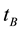
where
Also, 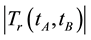
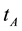
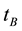
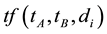
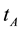
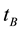
Definition 3
A minimal support 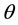
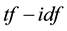
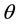
2.3. Semantic Clique
We observed that the set of association rules for a collection of documents formed a semantic clique. We believed that each connected component in the semantic clique represented a theme. The following section introduces semantic clique and defines some related concepts:
Definition 4 A semantic clique can be represented as a weighted hypergraph 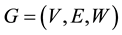
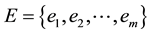
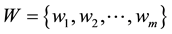
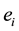
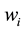
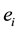
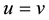
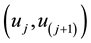
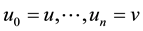
2.4. Design of Semantic Clique Aggregation Algorithm
Figure 1 shows an example of the semanticclique. This semantic clique is closed because of apriori conditions. The goal of this research was to establish the belief―a connected component of a clique represented a theme in the collection of documents.
In the graph, the vertex set 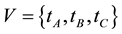
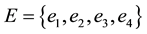
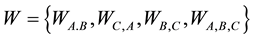
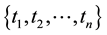
Figure 1. An example of clique.
Definition 5 The 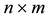
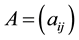
The corresponding weighted incidence matrix
where the weight 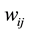
Each vertex in V represents a term that has been reserved, which means its support is greater than a given minimal support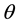
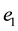
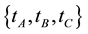
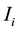
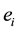
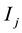
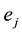

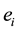
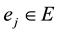
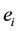
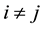
The one component is organized hyperedge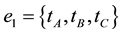
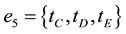
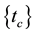
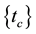
Figure 2. A clique with two maximal 3-connected components.
All the hyperedges in 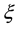
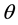
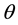
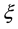
The documents can be decomposed into several categories, based ontheirsimilar concept, which is represented by a hyperedge in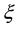
2.5. Evaluation of the Algorithm
2.5.1. Datasets
Four datasets were used to evaluate the effectiveness of the designed algorithm.
First dataset-the first dataset was web pages collected by Boley [16] . The web pages consist of four broad categories-business, finance, electronic communication, networking, labor, and manufacturing. Each categoryis divided into four subcategories.
The second dataset―the second dataset was the Reuters-21,578-Distribution-1 collection, which consisted of Newswire articles. Reuter-21,578 is a multi-class and multi-labeled benchmark, containing over 21,000 Newswire articles assigned to 135 so-called topics. These topics are used to evaluate the performance of clustering. The articles have a title and a content section, which refer to financial news related to different industries, countries, and other categories. Some articles contain many category labels, and documents in each category have a broader range of contents. Two kinds of tests were performed on this dataset. In this study, we selected 9494 documents from which all multi-categorized documents were discarded, and the categories with less than five documents were removed.
Third dataset―the third dataset was 848 electronic medical literature abstracts collected from PubMed. All those abstracts were collected by searching the keywords-cancer, metastasis, gene, and colon. The purpose was to differentiate all articles explaining to which organ cancer may spread from the primary tumor. A few organswere selected for this study such as liver, breast, lung, brain, prostate, stomach, pancreas, and lymph. In this study, we neglected the primary tumor present in the colon or from the other organs.
Fourth dataset―the fourth dataset is 305 electronic medical kinds of literature collected from the journals- Transfusion, Transfusion Medicine, Transfusion Science, Journal of Pediatrics and Archives of Diseases in Childhood Fetal and Neonatal Edition. Those articleswere selected by searching keywords―transfusion, newborn, fetal and pediatrics. The third and the fourth datasets belonged to homogeneous topics. They both denote a similar concept hierarchy.
2.5.2. Evaluation Criteria
To measure the effectiveness, we validated the themes generated as clustering results by the human experts as shown in Table 1.
The three measures of the effectiveness of a clustering method, precision, recall, and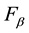
The 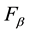
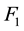
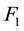
3. Results
3.1. First Dataset
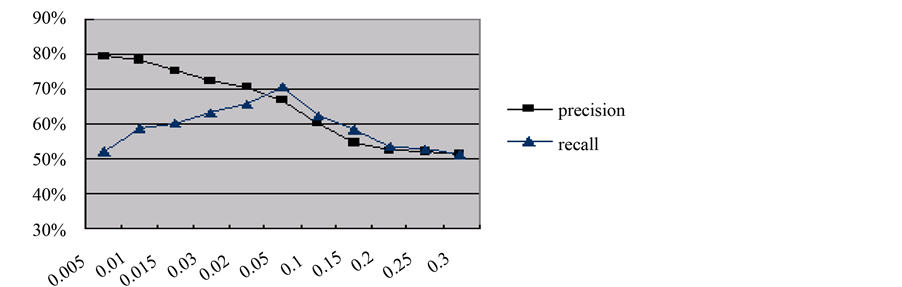
Table 2 demonstrates the results of the first experiment. Figure 3 demonstrates the performance on the first dataset of SCA.
3.2. Second Dataset
Table 3 indicates the evaluation results using the Reuter dataset and Table 4 illustrates some selected category results.
Table 1. Contingency table for category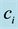
Table 2. The performance comparison on the first dataset.
Table 3. The performance of reuter dataset by semantic clique aggregation.
Table 4. The performance of some selected categories using reuter dataset by semantic clique aggregation.
Figure 3. The effectiveness of semantic clique aggregation on the first dataset.
3.3. Third Dataset
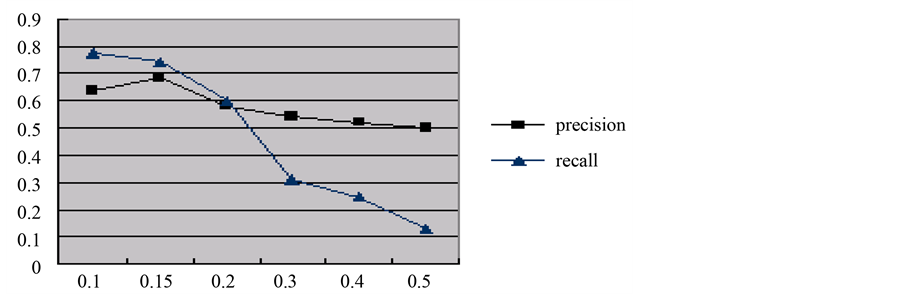
Figure 4 demonstrates the generated clique associated with minimal support, 0.1, whereas the effectiveness of the third dataset is shown in Figure 5.
3.4. Fourth Dataset
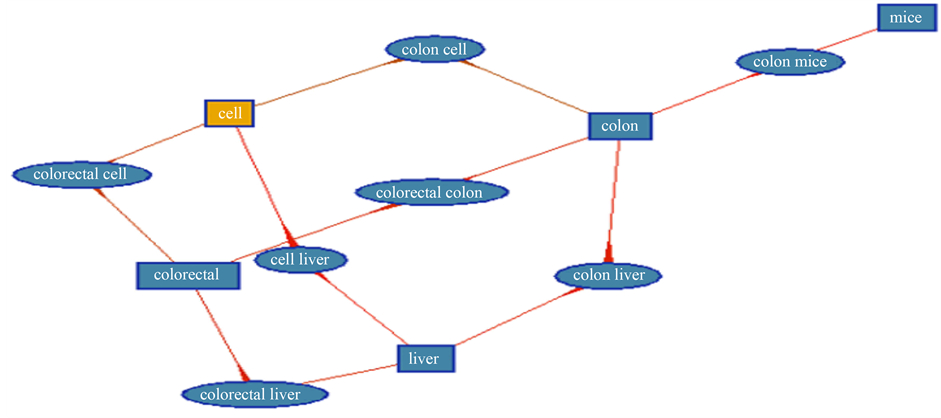
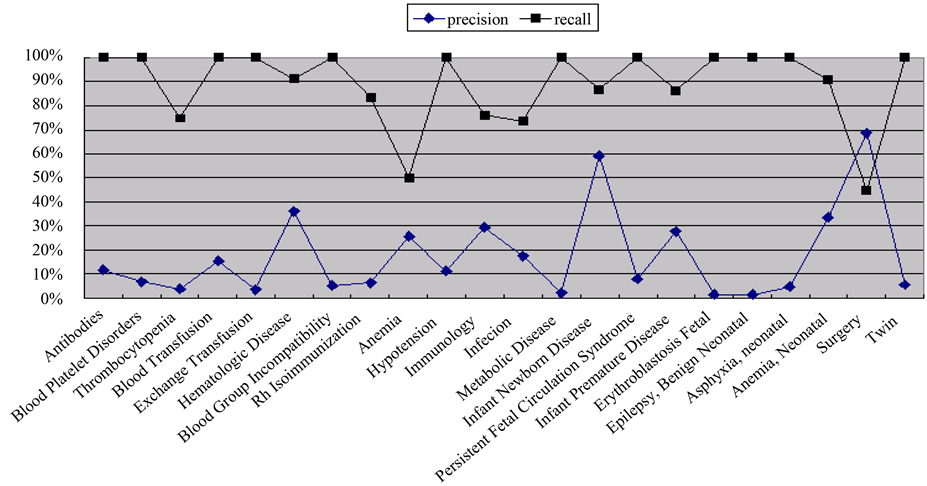
Figure 6 shows 516 documents, clustered according to the term colon and liver, whereas Figure 7 shows the effectiveness of all categories.
Figure 4. The semantic clique generated from the third dataset with minimal support, 0.1, whichever the rectangle node represents a vertex, and elliptic node represents a hyperedge, a semantic clique.
Figure 5. The effectiveness of semantic clique aggregation on the third dataset.
Figure 6. The 516 documents clustered according to the terms colon and liver.
Figure 7. The effectiveness of SCA on the fourth dataset with minimal support.
4. Discussion
4.1. Principal Findings
We found a novel method for document clustering that uses SCA algorithm. This agglomerative method did not use any distance function. A semantic clique was constructed from the set of co-occurring frequent terms in the text documents. The r-hyperedges (r-connected components) represented basic themes in the document collection. We presented a straightforward algorithm that could effectively discover the maximally connected components of co-occurring frequent terms in cluster documents. The results also showed that the value of “r” is dependent on the given minimal support. The r-connected component represents r-frequent itemsets with “r” different terms. The number of co-occurring terms decreases with a higher minimal support value for organizing themes in a collection of documents-higher the minimal support value, lower the value of r. The support for the generaltheme is higher than the specifictheme.
4.2. Secondary Findings
The proposed method was compared with conventional clustering methods such as PDDP, k-means, Auto Class, and HAC by using the four datasets. The SCA algorithm demonstrated superior performance towards document clustering. The results (Tables 2-4 and Figures 3-7) demonstrate that cliques are a good model to represent association rules in the text, which is particularly useful for automatic document clustering. The results are further discussed below.
4.2.1. Evaluation of SCA by Comparing with PDDP, k-Means, Auto Class, HCA by Using the First Dataset
Table 2 shows a comparison result of the SCA algorithm with PDDP, k-means, Auto Class and HCA after considering all non-stop words with the minimal support 0.15. The PDDP algorithm hierarchically splits the data into two subsets and derives a linear discriminant function from them based on the principal component analysis. The PDDP algorithm considered of all non-stop words. The principal component analysis often adversely affects the results of classification with sparse and high dimensional datasets, which induces a high false positive rate and false negative rate. The hyperedges generated by PDDP is based on the average Confidences of the Frequent Itemsets with the same items. It would be unfair that a possible theme is withdrawn, in the case; a small confidence of an itemset existed. In the first dataset, there are 47 clusters, maximally connected components, has been generated by SCA. It is larger than the original 16 clusters. The number of clusters reduces to be 23 after decreasing the Minimal support Value to 0.1, and its precision, recall, and F1 become 63.7%, 77.3%, and 0.698 respectively. Where there is higher the minimal support value, there is lower the number of co-occurred terms in a semantic clique. The precision is worse in PDDP with lower minimal support because the clustering constraints generated from hyperedges are stronger to filter some documents (high false positive rate).
4.2.2. Evaluation Conducted Using the Second Dataset
Table 3 shows the evaluation conducted on the Reuter dataset for the cluster numbers ranging from 2 to 5. For each given cluster number “k”, the performance scores were obtained by averaging “k” randomly chosen clusters from the Reuter corpus in a one-run test. Some terms, which indicate a generic category in Reuter classifications, do not designate the same category so that the number of clusters is larger than the number of Reuter’s categories. Table 4 illustrates some selected category results. Each clusteris labeled by selecting the most occurred concept for all its documents. Considering the Oil topic in the Reuter dataset, it is a com- positetopic, including Vegetable Oil, Crude Oil, and so on. There is about 1215 Reuter news clustered into the Oil group, of which 1156 documents were exactly on the Oil topic. Ninety-five percent (95%) documents correctly clustered into Oil. Some misclassified documents in Oil were related to Gas or Fuel. Strictly speaking, those documents were said correctly classified. The other misclassified 19 documents were Reuter CPI (Consumer Price Index) topics, which described the change of the CPI was related to the change in oil prices. The subcategory Crude Oil of the cluster contains 520 (44%) documents, which induced 88% precision rates compared with the Reuter’s crude oil.
4.2.3. Evaluation Conducted Using the Third Dataset
Fourteen organs related words were selected for clustering from the datasets consisting of PubMed abstracts. Figure 4 demonstrates the generated semantic clique associated with minimal support, 0.1. The ellipse nodes in Figure 4 denote the generated maximal connected components. Each identifies a cluster for document categorization. The effectiveness of the third dataset is shown in Figure 5.
4.2.4. Evaluation Conducted Using the Fourth Dataset
Five hundred sixteen (516) documents were clustered into a category in accordance with a maximal connected component generated from two terms colon and liver (Figure 6). This study allows documents to be soft categorized into several clusters due to their overlapped themes, which is producedby the commonly co-occurring terms associations. The MeSH categories (22 categories) were used to evaluate the effectiveness of SCA (Figure 7) on each category of the fourth dataset. The document clustering is based on the MeSH terms related to transfusion and pediatrics. The MeSH categories are a hierarchical structure that some categories are the subcategories of the other categories. Many theme categories shared the same terminology that induces a high false negative rate by SCA on document clustering. In the dataset documents are not uniformly distributed in all categories, some categories only contain a few documents that make their latent themes restricted by a few terms, for example, the anemia and the surgery categories whose precision are both below 70%.
4.3. Limitation and Future Studies
We tested the algorithms using the four datasets; however, the further testing with even more massive datasets could be performed. The algorithm is potentially useful for mining big data at the cloud. We tested the algorithm in the non-cloud environment, and it can be further tested in cloud-based enormous data to find its suitability.
5. Conclusion
We found that Semantic Clique Aggregation is a good model for document clustering. A group of strong term association can clearly identify a theme, and design of SCA algorithm has proved to be an effective way to find term associations in a collection of documents. The document clustering using SCA might be a useful approach to building search tools for semantic mining of big data in the cloud computing, Internet, and World Wide Web.
Acknowledgements
This research project was supported by grants from NSC 96-2221-E-038-004 and NSC 97-2221-E-038-006.
Cite this paper
AjitKumar,I-JenChiang,11, (2015) Document Clustering Using Semantic Cliques Aggregation. Journal of Computer and Communications,03,28-40. doi: 10.4236/jcc.2015.312004
References
- 1. Ranganathan, P. (2011) The Data Explosion. IEEE Computer Society Press, 39-48.
http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.204.6768&rep=rep1&type=pdf - 2. McAfee, A., Brynjolfsson, E., Davenport, T. H., Patil, D. J. and Barton, D. (2012) Big Data. The Management Revolution. Harvard Business Review, 90, 61-67.
- 3. Delbru, R., Campinas, S. and Tummarello, G. (2012) Searching Web Data: An Entity Retrieval and High-Performance Indexing Model. Web Semantics: Science, Services and Agents on the World Wide Web, 10, 33-58.
http://dx.doi.org/10.1016/j.websem.2011.04.004 - 4. Wu, X., Zhu, X., Wu, G.Q. and Ding, W. (2014) Data Mining with Big Data. IEEE Transactions on Knowledge and Data Engineering, 26, 97-107.
- 5. Joshi, A. and Jiang, Z. (2002) Retriever: Improving Web Search Engine Results Using Clustering. TEAM, 2002, 59-81.
http://dx.doi.org/10.4018/978-1-930708-12-9.ch004 - 6. Jonquet, C., LePendu, P., Falconer, S., Coulet, A., Noy, N.F., Musen, M.A. and Shah, N.H. (2011) NCBO Resource Index: Ontology-Based Search and Mining of Biomedical Resources. Web Semantics: Science, Services and Agents on the World Wide Web, 9, 316-324.
http://dx.doi.org/10.1016/j.websem.2011.06.005 - 7. Hogan, A., Harth, A., Umbrich, J., Kinsella, S., Polleres, A. and Decker, S. (2011) Searching and Browsing Linked Data with SWSE: The Semantic Web Search Engine. Web Semantics: Science, Services and Agents on the World Wide Web, 9, 365-401.
http://dx.doi.org/10.1016/j.websem.2011.06.004 - 8. Harth, A. (2010) VisiNav: A System for Visual Search and Navigation on Web Data. Web Semantics: Science, Services and Agents on the World Wide Web, 8, 348-354.
http://dx.doi.org/10.1016/j.websem.2010.08.001 - 9. Fazzinga, B., Gianforme, G., Gottlob, G. and Lukasiewicz, T. (2011) Semantic Web Search Based on Ontological Conjunctive Queries. Web Semantics: Science, Services and Agents on the World Wide Web, 9, 453-473.
http://dx.doi.org/10.1016/j.websem.2011.08.003 - 10. Kosala, R. and Blockeel, H. (2000) Web Mining Research: A Survey. ACM SIGKDD Explorations Newsletter, 2, 1-15.
http://dx.doi.org/10.1145/360402.360406 - 11. Mladenic, D. (1999) Text-Learning and Related Intelligent Agents: A Survey. IEEE Intelligent Systems, 14, 44-54.
http://dx.doi.org/10.1109/5254.784084 - 12. Chatterjee, R. (2012) An Analytical Assessment on Document Clustering. International Journal of Computer Network and Information Security (IJCNIS), 4, 63-71.
http://dx.doi.org/10.5815/ijcnis.2012.05.08 - 13. Shah, N. and Mahajan, S. (2012) Semantic Based Document Clustering: A Detailed. International Journal of Computer Applications, 52, 42-52.
http://dx.doi.org/10.5120/8202-1598 - 14. MacQueen, J. (1967) Some Methods for Classification and Analysis of Multivariate Observations. Proceedings of the Fifth Berkeley Symposium on Mathematical Statistics and Probability, 1, 281-297.
- 15. Cheeseman, P. and Stutz, J. (1996) Bayesian Classification (Auto Class): Theory and Results. In: Fayyad, U.M., Piatetsky-Shapiro, G., Smyth, P. and Uthurusamy, R., Eds., Advances in Knowledge Discovery and Data Mining, American Association for Artificial Intelligence, Menlo Park, 153-180.
- 16. Boley, D., Gini, M., Gross, R., Han, E.H.S., Hastings, K., Karypis, G. and Moore, J. (1999) Document Categorization and Query Generation on the World Wide Web Using WebACE. Artificial Intelligence Review, 13, 365-391.
http://dx.doi.org/10.1023/A:1006592405320 - 17. Jain, A.K. and Dubes, R.C. (1988) Algorithms for Clustering Data. Prentice-Hall, Inc., Upper Saddle River.
- 18. Chiang, I.J., Lin, T.Y. and Hsu, J.Y.J. (2004) Generating Hypergraph of Term Associations for Automatic Document Concept Clustering. Proceedings of the 8th IASTED International Conference on Artificial Intelligence and Soft Computing, Marbella, 1-3 September 2004, 181-186.
- 19. Maron, M.E. and Kuhns, J.L. (1960) On Relevance, Probabilistic Indexing and Information Retrieval. Journal of the ACM (JACM), 7, 216-244.
http://dx.doi.org/10.1145/321033.321035 - 20. Fuhr, N. and Buckley, C. (1991) A Probabilistic Learning Approach for Document Indexing. ACM Transactions on Information Systems (TOIS), 9, 223-248.
http://dx.doi.org/10.1145/125187.125189 - 21. Salton, G. and Michael, J.M. (1986) Introduction to Modern Information Retrieval. McGraw-Hill, Inc., New York.
- 22. Salton, G. and Buckley, C. (1988) Term-Weighting Approaches in Automatic Text Retrieval. Information Processing & Management, 24, 513-523.
http://dx.doi.org/10.1016/0306-4573(88)90021-0 - 23. Sparck Jones, K. (1972) A Statistical Interpretation of Term Specificity and Its Application in Retrieval. Journal of Documentation, 28, 11-21.
http://dx.doi.org/10.1108/eb026526 - 24. Moffat, A. and Zobel, J. (1994) Compression and Fast Indexing for Multi-Gigabyte Text Databases. Australian Computer Journal, 26, 1-9.
- 25. Feldman, R., Fresko, M., Kinar, Y., Lindell, Y., Liphstat, O., Rajman, M. and Zamir, O. (1998) Text Mining at the Term Level. In: Zytkow, J.M. and Quafafou, M., Eds., Principles of Data Mining and Knowledge Discovery, Springer, Berlin Heidelberg, 65-73.
http://dx.doi.org/10.1007/BFb0094806 - 26. Feldman, R., Dagan, I. and Kloesgen, W. (1996) Efficient Algorithms for Mining and Manipulating Associations in Texts. Proceedings of the Thirteenth European Meeting on Cybernetics and Systems Research, Vienna, 9-12 April 1996, 949-954.
- 27. Feldman, R. and Hirsh, H. (1996) Mining Associations in Text in the Presence of Background Knowledge. Proceedings of the Second International Conference on Knowledge Discovery and Data Mining, Portland, 2-4 August 1996, 343-346.
- 28. Agrawal, R., Imieliński, T. and Swami, A. (1993) Mining Association Rules between Sets of Items in Large Databases. ACM SIGMOD Record, 22, 207-216.
http://dx.doi.org/10.1145/170036.170072